Simulating and Numerical Solution of Stochastic Differential Systems with Switching Diffusion during the Firing
S. Sarabadan1, *, H. R. Shaahrza2
1Departeman of Mathematics, Imam Hossein University, Tehran, Iran
2Departeman of Mathematics, Sharif University, Tehran, Iran
Abstract
Launching the Ramp is one of the primary means of defence. Rocket stability in lunching has been very effective in accurate hitting the object which fully depends on the conditions and lunching oscillation. In this paper we consider a stochastic differential model with switching Diffusion for rocket system and with using the generalization of the Taylor-method, we will estimate the answer of this problem. Finally the results of numerical solution is presented in Sci-lab.
Keywords
Sloped Rocket Launching, Oscillations, Switching Diffusion, Stochastic Differential Systems
Received:July 24, 2016
Accepted: August 15, 2016
Published online: August 25, 2016
@ 2016 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY license. http://creativecommons.org/licenses/by/4.0/
1. Introduction
In this study, for detailed design and efficient lunching system, especially in the early non-guided launching of rocket, review of the oscillation is important and necessary. We suppose that the launching device and the moving rocket form a complex oscillating system that join together a sum of rigid bodies bound by elastic elements (the vehicle chassis, the tilting platform and the rockets in the containers [1].
Suppose the independent unknown dynamic variables of the rocket-launching device system motion are presented in the form of the following column vector [2]:
![]() (1)
(1)
Where the vehicle chassis translation zs, the vehicle chassis rotation γy (the chassis pitch movement), the vehicle chassis rotation γx (the chassis rolling movement), the tilting platform rotation ρz(the gyration movement around the vertical axes), the tilting platform rotation ρy (the pitch movement) and the rocket translation s.
So, one can obtain the matrix form of the stochastic differential equations system that describes the rocket launching system components motion:
![]() (2)
(2)
Where B6×6=(b i, j)i=1,6j=1,6 is the matrix of the velocities coefficients, Ẋ6 x 1; C6×6=(c i, j)i=1,6j =1,6 is the matrix of the unknown variables coefficients X. N6×15=(n i, j)i=1,6j=1,15 is the matrix of the coefficients for the nonlinear combinations of the unknown variables:
![]() (3)
(3)
For more information about the components of matrices (3), that can be specified randomly, one can see [1,2]. And, the F6×3=(f i, j) i=1,6j=1,3 is the matrix of the external forces that acts on the system:
![]() (4)
(4)
The vector (4) is used to express the influence of the external forces on the motion system. In this vector, the first term corresponds to the weight force, the second term corresponds to the rocket thrust and the last term to the rocket jet force [2].
In this equation K=(ki,j)i=1,6j=1,6 is the noise matrix of coefficients that is because of the uncertain of all conditions.
In this work, ε6 x1 are assumed as the normal independent variables [3]
Stochastic differential equations (SDEs) provide a foundation for many branches of applied sciences. Indeed, they ensure an adequate description for systems subjected to random disturbances. SDEs represent a major object of research in modern control theory. The significance of such equations is also explained by their close connection to equations arising in mathematical physics.
A well-known (yet, promising) approach to numerical integration of Ito SDEs proceeds from the stochastic analogs of Taylor expansion. Theoretically, this formula allows designing methods with arbitrary large orders of accuracy (under appropriate assumptions regarding the coefficients of combined equations).
An important distinguishing feature of the stochastic analogs of Taylor expansion used to solve Ito SDEs lies in the following. These analogs incorporate the so-called repeated stochastic integrals (of the Ito or Stratonovich type) being complex functional of the components of the n-dimensional Wiener process [3]. In Ito’s theory, Hermite polynomials serve as analogs of standard degrees of the Wiener process. On the other part, the exponential super martingale duplicates the standard exponent of a stochastic integral. In the sense of the mean-square convergence criterion, the problem of joint numerical simulation of sets of repeated Ito stochastic integrals appears complicated, both theoretically and practically.
Recently, researchers have focused their attention on mathematical models in the form of SDEs with Markovian jumps of the diffusion component. They are called switching diffusion models.
Such mathematical objects describe complex systems subjected to abrupt changes in their structure and parameters (due to possible failures, disrupt data communication and impacts of an external environment). Switching diffusion models gain growing popularity in modern control theory and information theory.
As a rule, investigators treat switching diffusions governed by finite-state Markov chains (Markovian switching). During computer simulation of such systems, it is necessary to solve numerically SDEs with Markovian switching. There exist publications dedicated to controllability, stability and stabilization of such systems.
However, the issues of numerical solution of SDEs with Markovian switching have been insufficiently explored.
The famous Euler method was considered in [3] for numerical solution of stochastic differential equations with Markovian switching; in addition, proofs for some special results were demonstrated. This paper verifies the applicability of numerical schemes based on stochastic analogs of Taylor expansion to approximate solutions of such equations.
The rest of the paper is organized as follows: In the Section 2, the generalized of the Taylor-method is expressed for solving the stochastic differential equation with switching diffusion. This method is applied to the problem for solving the stochastic differential equation for launching of rocket in Section 3. The numerical results are shown in the Section 4.
2. Review on the Solution of the Stochastic Differential Equation with Switching Diffusion
Let (Ω, F, P) be a probabilistic space, Ft (t0 ≤ t ≤ t0 + T) represent a non-decreasing family σ comprising sub algebras of F, and (ωr(t), Ft), r = 1,..., d, indicate independent Wiener processes.
Consider the Ito stochastic differential equation:
![]() (5)
(5)
Where X, a, and ![]() mean vectors of length n.
mean vectors of length n.
The functions a(t, x) and ![]() are given and continuous under t ∈ [t0, t0 + T], x ∈ _n. Moreover
are given and continuous under t ∈ [t0, t0 + T], x ∈ _n. Moreover
They meet the Lipschitz condition for all t ∈ [t0, t0 + T], x ∈ _n, y ∈ _n:
![]() (6)
(6)
In the sequel, we adopt the following notation: |x| defines the Euclidean norm of the vector x; xy yields the scalar product of the vectors x and y; K is a positive constant; X t,x(t) or simply X(t) specifies the solution of Eq. (5)
Define the following one-step approximation ![]() t,x(t + h), t0 ≤ t ≤ t + h ≤ t0 + T, which is generated depending on x, t, h, and {ω1(ϑ) − ω1(t),..., ωd(ϑ) − ωd(t) : t ≤ ϑ ≤ t + h}:
t,x(t + h), t0 ≤ t ≤ t + h ≤ t0 + T, which is generated depending on x, t, h, and {ω1(ϑ) − ω1(t),..., ωd(ϑ) − ωd(t) : t ≤ ϑ ≤ t + h}:
![]() (7)
(7)
Assume that (Ω, F, P) is a probabilistic space, Ft (t0 ≤ t ≤ t0 + T) represents a non-decreasing family comprising σ-sub algebras of F, and ωr(・), r = 1,..., d, indicate independent Wiener processes. Let M = {1,...,m} be a finite set.
Consider the following stochastic differential equation with Markovian switching:
![]() (8)
(8)
The transient function of such process is defined by a set of functions P(t, u, l) = pul(t); they form the stochastic matrix P(t) of transition rates (pul(t) ≥ 0, l pul(t) = 1). The values pul act as the probabilities of transition from u to l during the period h (under the condition that the process β(t) leaves state u during this period).[4]
The evolution of the whole process β(t) is described by the values qul, ql. The latter form the transition intensity matrix
![]() (9)
(9)
For each t, we have qul(t) ≥ 0 under quu=-qu, ![]() for each u ∈M [1].
for each u ∈M [1].
Suppose that the functions a(β(t), x(t)) and σr(β(t), x(t)) are defined, enjoy the continuity property for t ∈ [t0, t0 +T], ![]() , as well as satisfy the Lipschitz condition for all t
, as well as satisfy the Lipschitz condition for all t ![]() [t0, t0 +T],
[t0, t0 +T], ![]() ,
, ![]() ,
, ![]()
![]() (10)
(10)
In addition, these functions meet the constraint.
![]()
(bounded velocity of components with respect to x). Under the stated conditions, Eq. (8) admits a unique continuous solution Xu,x on the interval t ≥ 0 for each initial condition [8].
Set the numerical solution problem for Eq. (9). In other words, it is necessary to approximate its solution on the above time interval. In this formulation, the transition intensity matrix Q turns out independent of x (but depends only on t). Thus, the problem can be reduced to the well-known solution problem for the stochastic differential Eq. (5)on a set of random subintervals [0, t1), [t1, t1 + t2),..., where tk designate random instants of switching in the Markov chain (they can be defined a priori). Recall that the next switching instant tk and the state β(tk) are random variables whose distribution depends only on (β(tk), tk). Therefore, one can generate a priori the set (β(tk), tk) of the right-hand sides of Eq. (1) and solve the latter through famous methods.
The approximation accuracy (which depends on step choice within separate subintervals) becomes reachable on the whole time interval. However, another solution procedure is applicable to (8), as well.
In the case of the stochastic differential Eq. (5), E. Platen proposed simple derivations (involving merely Ito’s formula) to expand the solution Xt,x(t + h) with respect to powers of h and integrals depending on the increments ωr(ϑ) −ωr(t), where t ≤ ϑ ≤ t +h, r = 1,..., d. In the deterministic setting, this expansion reproduces Taylor’s formula for Xt,x(t+h) with respect to powers of h in a neighborhood of the point (t, x) [4]. In what follows, we employ Platen’s expansion (see [4] for details) to solve Eq. (8). For this, substitute the function f(t, x) by the function f(β(t), x(t)) with the switching component.
Such approach was adopted in [4,8]; the cited authors presented the corresponding lemmas and theorems in a special case (Euler’s scheme studied in these works represents a particular case of the scheme.
However, in the model of state-dependent switching, numerical solution leads to the following. Switching instants and post-switching states are also estimated approximately. Here a series of questions arise concerning proper interpretation of the difference between the approximate solution and its exact counterpart. Probably, one should introduce a certain measure for the deviation of the approximate distribution of switching instants from their exact distribution. An admissible way is to modify such measure (making all jumps Poisson jumps); subsequently, the problem acquires another form. It is necessary to assess (5)the deviation of such measure from the exact one and(2) the difference between the estimated mean values of the functionals and the exact values.
3. Solving the Stochastic Differential Equation with Switching Diffusion for Launching of Rocket
At first, to solve the equation, system (2) has been changed to the form of (5)
![]()
In top equation, the coefficients must satisfy the LIPSCHITZ property. Since the coefficients of the equation are linear, they apply in this condition and the generalized of the Taylor-method with switching Diffusion can be used, one can see.
In addition Markov- model can be examined by the generalized of the Taylor-method with switching diffusion. So all modes of projectiles and rockets from beginning of firing to ending are used for Markov states.
According to this, the system (1) is reduced to first order stochastic differential equation.
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
Using those new variables (11)-(16), the unknown variables vector can be presented as follows [2]:
![]() (17)
(17)
Using the notations (11)-(16) and the vector (17), as well as the equation (2), we obtain the new matrix form of the first order differential equations, which describes the motion of the rocket-launching device system:
![]() (18)
(18)
Where,
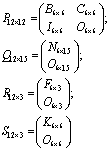 (19)
(19)
Which ![]() ,
,![]() and
and ![]() are zeros matrices and as mentioned before other blocks are the random matrices that their elements are random values imposing the launching device during the firing. Here, we solve the matrix system (18) by applying radial basis functions. The 6 scalar equations are necessary to calculate the 6 unknown variables that describe the movement of the rocket-launching device system during firing (
are zeros matrices and as mentioned before other blocks are the random matrices that their elements are random values imposing the launching device during the firing. Here, we solve the matrix system (18) by applying radial basis functions. The 6 scalar equations are necessary to calculate the 6 unknown variables that describe the movement of the rocket-launching device system during firing (![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ) while the other scalar equations allow to compute the evolutions of the differentials of 6 main unknown variables defined with (11)-(16) [2].
) while the other scalar equations allow to compute the evolutions of the differentials of 6 main unknown variables defined with (11)-(16) [2].
At first, the formula is assumed to solve the above equations,
Assume that (Ω, F, P) is a probabilistic space, Ft (t0 ≤ t ≤ t0 + T) represents a non-decreasing family comprising σ-sub algebras of F, and ωr(・), r = 1,..., d, indicate independent Wiener processes. Let M = {1,...,m} be a finite set. Consider the following stochastic differential equation with Markovian switching:
![]() (20)
(20)
To find solution to Eq. (20), we propose the following numerical scheme based on the one-step approximation (with the root-mean-square order of accuracy of 3/2 ):
 )21(
)21(
4. Numerical Results
In this section, expansion of the Taylor-method with switching Diffusion is tested for solving the system (18). All numerical results carried out with Sci-lab. The approximation of the components of ![]() are shown in figural form. (The differential of oscillations parameters of rocket-launching device)
are shown in figural form. (The differential of oscillations parameters of rocket-launching device)
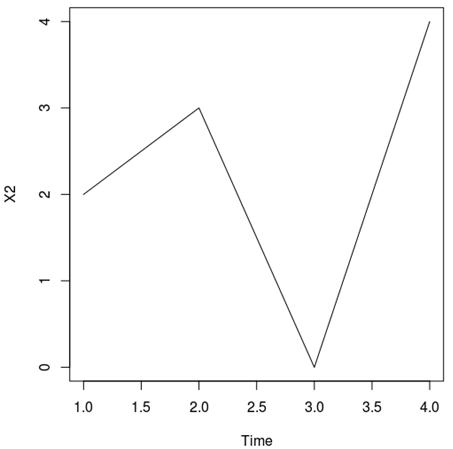
Fig. 1. X1 changes over time.

Fig. 2. X2 changes over time.

Fig. 3. X3 changes over time.

Fig. 4. X4 changes over time.
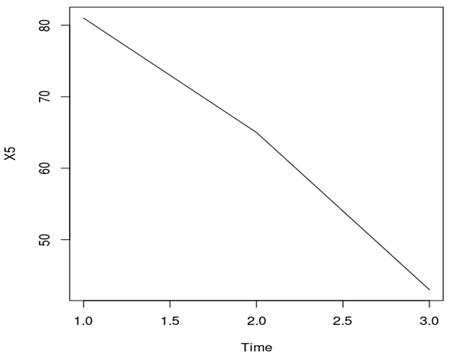
Fig. 5. X5 changes over time.

Fig. 6. X6 changes over time.
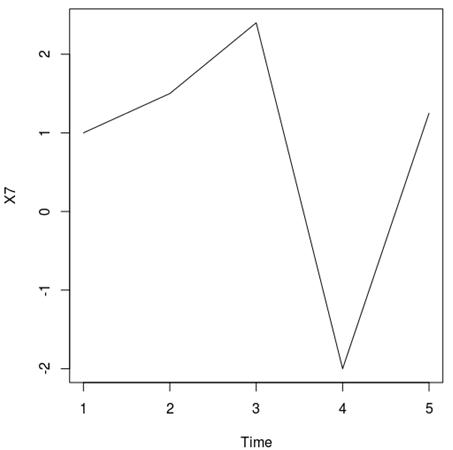
Fig. 7. X7 changes over time.

Fig. 8. X8 changes over time.
Fig. 9. X9 changes over time.
Fig. 10. X10 changes over time.
Fig. 11. X11 changes over time.
Fig. 12. X12 changes over time.
Notations and Symbols
|
| Independent unknown dynamic variables of the rocket-launching device system motion |
|
| Vehicle chassis translation |
|
| Chassis pitch movement |
|
| Chassis rolling movement |
|
| Gyration movement around the vertical axes |
|
| Pitch movement |
|
| Rocket translation |
|
| Matrix of the coefficients for the nonlinear |
|
| External forces that acts on the system |
|
| Shape parameter |
|
| Euclidean distance |
|
| Set of center |
|
| Derivative of s |
|
| Derivative of |
|
| Derivative of |
|
| Derivative of |
|
| Derivative of |
References
- P. Somoiag, C. Moldoveanu, Numerical research on the stability of launching devices during firing, Defence Technology 9, (2013), 242-248.
- P. Somoiag, F. Moraru, D. Safta, C. Moldoveanu, A mathematical model for the motion of a rocket-launching device system on a heavy vehicle, Military technical academy, Romania, (2012).
- Jagadeep Thota · Brendan J. O’Toole Mohamed B. Trabia Optimization of shock response within a military vehicle space frame(2011):847–861.
- Arzamas Polytechnic Institute of Alekseev Nizhni Novgorod State,Technical University,Numerical Solution Algorithms for Stochastic Differential Systems with Switching Diffusion (2011).
- R. Schaback, Improved error bounds for scattered data interpolation by radial basis functions, Math Comput, 68, (1999), 201-206.
- Kuznetsov, D.F., Stokhasticheskie differentsial’nye uravneniya: teoriya i praktika chislennogo resheniya (Stochastic Differential Equations: Theory and Practice of Numerical Solution), St. Petersburg: Politekh.Univ., 2007.
- Kuznetsov, D.F., Stochastic Differential Equations: Theory and Practice of Numerical Solution, Differ.Uravn. Prots. Upravlen., 2008, no. 1.
- Yin, G., Mao, X., Yuan, C., and Cao, D., Approximation Methods for Hybrid Diffusion Systems with State-dependent Switching Processes: Numerical Algorithms and Existence and Uniqueness of Solutions,SIAM J. Math. Anal., 2010, vol. 41, no. 6, pp. 2335–2352.
- N. Katz, H. Mukai, H. Schattler, M. Zhang,6 and M. Xu, Solution of a Differential Game Formulation of Military Air Operations by the Method of Characteristics,(2005).
- Lee B, Saitou K Three-dimensional assembly synthesis for robust dimensional integrity based on screw theory. J Mech (2006):57–65.
- Yuan, C. and Lygeros, J., Stochastic Markovian Switching Hybrid Processes, Project IST-2001-38314,COLUMBUS, Design of Embedded Controllers for Safety Critical Systems, Cambridge: Univ. of Cambridge, 2004.



