The Modelling of the Synchronization Problem with Colored Petri Nets

Goharik R. Petrosyan^*

International Scientific-Educational Center of the National Academy of Sciences, Yerevan, the Republic of Armenia

Abstract

The work is done to show the modeling of Patil synchronization problem with the support of Colored Petri Net, which was impossible to present with well known P and V operations or through Classical Petri Net [1], as the limitation of the mentioned mathematical properties does not allow to model the mechanisms, where the process must be synchronized with optimal allocation of resources. The work explains the modeling features of the synchronization function with Colored Petri Net. There is a detailed description of Patil proposal on synchronization issue of cigarette smokers with Colored Petri Net (Fig. 2.), which shows due to what exact properties of expansion occurred (guarding types to positions and tokens, guarding logical expressions to transitions and arcs, importing of high-level special properties, special for programming languages) and how to manage the process of resolving such problems through modern mechanisms of modeling. The described model below illustrates the most important qualities of the Colored Petri Net which allows to increase the potential for modeling with Colored Petri Net, and gives possibility of modelling for more detailed examination for such problems.

Keywords

Synchronization Problem, Colored Petri Net, P and V Operations, Classical Petri Net, The Cigarette Smoker’s Problem, Token, Position, Transition, Arc, Guard

Received:August 10, 2016
Accepted: August 29, 2016
Published online: September 8, 2016

@ 2016 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY license. http://creativecommons.org/licenses/by/4.0/

1. Introduction

In modern society informational communication and confidential usage of it, became a common matter and is quite used by many. One of the important areas of application is Petri Net theory. The main problem of Petri Net is modeling of real-time systems by optimization of the processes with clear description. Therefore, Petri Net computer system gives opportunities to study properties, use them to solve practical problems, mainly those issues that are related to information processing models, paralleled with sources and consider to be important issue [1-4]. In such cases we need to use Petri Net. The following problems may serve as examples for problems that often occur in discrete systems, the problem of synchronizing in need of design and research:

• The system uses the functions for which it is intended?

• Whether it operates effectively?

• There may be some errors and emergency situations?

• Are there potential barriers and if it is possible to simplify the system or replace individual components with more advanced components, without prejudice to its general functions?

• If it's possible to design more complicated and more functional systems that will meet the requirements and so on.

Definition. Petri Net  pair, where  is the network structure and  is the network condition. In structure  of a -positions, -transitions are finite sets.  are the input and output functions, respectively, where  are all possible collections (repetitive elements) of .  is the function of condition, where  is the set of integers. We determine (in a known manner) the allowed transitions of Petri Nets and the transitions from one state to another, as well the set of reachable states.

Places, transitions, tokens and arcs are the basic Petri Net components. A Petri Net can be thought of as a bipartite graph consisting of two types of nodes, places and transitions. Places are displayed pictorially as circles (or ovals) and transitions are displayed as vertical lines. Shifts of tokens are define the state of the system.

The simple presentation of system by Petri Net is based on two conceptions-events and conditions. Event is an action which occurs in the system. The appearance of the events governs the state of the system. The state of the system can be described by multiple conditions.

The condition is a predicate or a logical description of the states of the system. The condition can admit true or false value. As the events are actions they can take place. In order the event occurs, is necessary appropriate existence of the conditions. They call these conditions the preconditions of the event. The appearance of the event can bring the break of the preconditions and bring to other carrying of the condition-postconditions.

Colored Petri Net (CPN) is Classical Petri Net modern expansion which was created by K. Jensen [3-6]. Colored Petri Nets (CP-nets or CPNs) is a modeling language developed for systems in which communication, synchronizing and resource sharing play an important role. CP-nets combine the strengths of Classical Petri Nets with the strengths of a high-level programming language. Petri Nets provide the primitives for process interaction, while the programming language provides the primitives for the definition of data types and the manipulations of data values.

A CPN model consists of a set of modules (pages) which each contain a network of places, transitions and arcs. The modules interact with each other through a set of well-defined interfaces, in a similar way as known from many modern programming languages. The graphical representation makes it easy to see the basic structure of a complex CPN model, i.e., understand how the individual processes interact with each other. CP-nets also have a formal, mathematical representation with a well-defined syntax and semantics. This representation is the foundation for the definition of the different behavioral properties and the analysis methods. Without the mathematical representation it would have been totally impossible to develop a sound and powerful CPN language. However, for the practical use of CP-nets and their tools, it suffices to have an intuitive understanding of the syntax and semantics. Programming languages are successfully applied for those who are not familiar with the formal, mathematical definitions of the languages.

CPN models can be made with or without explicit reference to time. Untimed CPN models are usually used to validate the functional/logical correctness of a system, while timed CPN models are used to evaluate the performance of the system. There are also other languages which can be used to investigate the functional/logical correctness of a system or the performance of it. However, it is rather seldom to find modeling languages that are well-suited for both kinds of analysis.

CP-nets can also be simulated interactively or automatically. In an interactive simulation the user is in control and we can see the effects of the individual steps directly on the graphical representation of the CP-net. In this case the user can investigate the different states and choose between the enabled transitions. An interactive simulation is similar to single-step debugging. It gives a way to "walk through" a CPN model, investigating different scenarios and checking whether the model works as expected. This is different compared with many off-the-shelf simulation packages which often act as black boxes, where the user can define inputs and inspect the results, but otherwise have very little possibility to understand and validate the models on which the simulations build. The insight and detailed knowledge of a system, which the users gain during the development and validation of a simulation model, is often as important as the results that the users get from the actual simulation runs.

It is necessary to execute the CPN models as fast and efficient as possible, without detailed human interaction and inspection. The user still needs to interpret the simulation results. According this, it is often suitable to use animated, graphical representations providing an abstract, application-specific view of the current state and activities in the system.

CP-nets also give more formal verification methods, known as state space analysis and invariant analysis. Also, industry systems are often so complex that it is impossible or at least very expensive to make a full proof of system correctness. Hence, the formal verification methods should be seen as a complement to the more informal validation by means of simulation. The use of formal verification is often restricted to the most important subsystems or the most important aspects of a complex system. CP-nets and their tools have been used in various practical projects within a large variety of different application areas. The CPN group at the University of Aarhus, Denmark, has developed two sets of computer tools.

Colored Petri Net is a graphical oriented language which is used for modeling, analysis, description and presentation systems [3-6]. Typical examples of application areas are communication protocols, distributed systems, automated production systems, work flow analysis and VLSI chips. In the classical or traditional Petri Net tokens do not differ from each other, we can say that they are colorless. In difference of Classical Petri Net in Colored Petri Net of a position can contain tokens of arbitrary complexity -a note, lists, etc., that makes reliable models more possible. The Design/CPN system is used for modeling "NOKIA" phones, in order to find out the unwanted functional interactions [3, 4].

Definition: A Colored Petri Net is a tuple  satisfying the following requirements:

(i)         is a finite set of non-empty types, called color sets.

(ii)        is a finite set of places.

(iii)      is a finite set of transitions.

(iv)      is a finite set of arcs such that:

•

(v)       is a node function. It is defined from into .

(vi)     is a color function. It is defined from  into .

(vii)    is a guard function. It is defined from  into expressions such that:

• .

(viii)  is an arc expression function. It is defined from , by expressions such that:

•

where  is the place of .

(ix)     is an initialization function. It is defined from into closed expressions such as:

•

Colored Petri Net consists of the following components:

The ellipses and the circles are called places. They describe the states of the system (buffers).

The rectangles are called transitions. They describe the actions (processes).

The arrows are called arcs. The arc expressions describe how the state of the CPN changes when the transitions occur.

Each place contains a set of markers called tokens, each of these tokens carries a data value, which belongs to a given type. The distribution of tokens, called marking, in the places of a CPN determines the state of a system being modeled. The dynamic behavior of a CPN is described in terms of the firing of transitions. The firing of a transition takes the system from one state to another. A transition is enabled if the associated arc expressions of all incoming arcs can be evaluated to a multi-set, compatible with the current tokens in their respective input places, and its guard is satisfied. An enabled transition may fire by removing tokens from input places specified by the arc expression of all the incoming arcs and depositing tokens in output places specified by the arc expressions of outgoing arcs [5].

2. Example of Colored Petri Net

Consider the simple example of a Colored Petri Nets, which is shown in Figure 1.

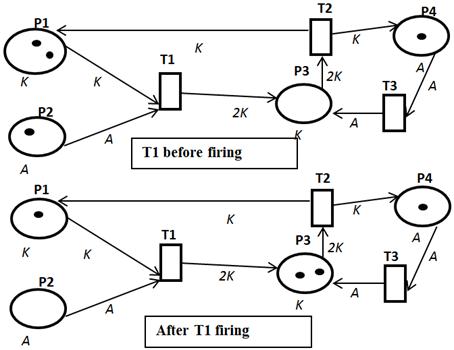
Fig. 1. Example of CPN T1 before firing and after T1 firing.

P1 and P3 positions include tokens of K type in Fig. 1, and P2, P4 positions include tokens of A type. After T1 transition firing transfers a token of K type by (P1, T1) arc, and transfers a token of A type by (P2, T1) arc (that is, unlike Classical Petri Nets the tokens aren’t homogeneous). Two tokens of K type are transfer by (T1, P3) arc, and there appear two tokens in P3. Before T1 transition firing, the state of the system is described by vector S1=(2,1,0,1), and after T1 transition firing will be S2=(1,0,2,1). Therefore, in the result of permissible transitions of firing we will have the set of reachable states of the system.

On a solution to the cigarette smoker’s problem with Colored Petri Nets.

In 1971 Patil proved that P- and V- actions have insufficient capacity for resolving synchronization issues. His proposed solution to model problem is called smoking a cigarette. The problem consists of four processes, which model the states and actions of the agent and 3 smokers. Each smoker continuously makes a cigarette and smokes it. To make and smoke the cigarette we need three ingredients: tobacco, paper and matches. One of the smokers always has the paper, the second smoker has tobacco, the third has the matches. The agent has unlimited number of the ingredients. The agent puts the two ingredients on the table, the smoker who has the third ingredient, can make the cigarette and then he signals the agent. In this case, the agent offers the other two ingredients, which are necessary for the smoker, and the action is repeated.

The actions of the smokers without the coordination are as follows.

Let X - the smoker with tobacco, Y - the smoker with paper, Z - the smoker with matches, A-agent.

The smokers' problem is then to define some additional semaphores and processes, if necessary, and to introduce necessary P and V statements in these processes so as to attain the necessary cooperation among themselves required ensuring continued smoking of cigarettes without reaching a deadlock. There is, however, a restriction that the process which supplies the ingredients cannot be changed and that no conditional statements may be used. The first restriction is placed because the smokers are seeking cooperation among themselves and therefore should not change the supplier, and the second restriction is justified because P and V primitives were introduced to avoid having to coordinate processes by repeatedly testing a variable until it changes its value, and because the operation of making and smoking a cigarette has no conditional actions. It will be seen that the cigarette smokers’ problem has no solution.

Patil showed that there is no sequence of P- and V- actions and can’t solve the problem correctly [1], [2]. If we try to model the problem with the Classical Petri Net, we will get a non-active net. Also, since all tokens in Classical Petri Nets have the same type, then ingredients will not be differed from each other.

The author modeled the problem with Colored Petri Net (Fig. 2), which gives the possibility of number of modeling for solving similar problems due to a number of properties, such as the existence of the attached data types, functions, transitions [3-10].

Position A presents the agent status, which has 3 types of tokens: (p, m) - (p-paper, m-match), (t, m) - (t-tobacco, m-match), (p, t) - (p-paper, t- tobacco), with the help of an organized net of cycle, it is possible to constantly offer 2 different ingredients to the smokers.

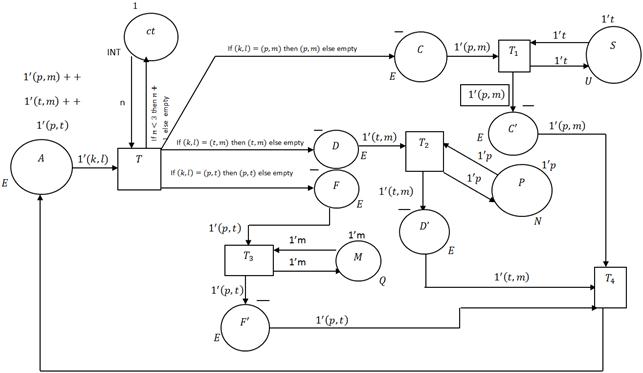
Fig. 2. The modeling of Cigarette smoker’s problem with Colored Petri Nets.

In position A and also in number of positions in the net, E type is attached, that is a combination of 3 types, which means the combination can be any one of these 3 types, and each of which is Cartesian product: with N and Q, U and Q, or N and U.  the pair of variables is a Cartesian product of E-type, that is either, or   or . C', D', F', C, D, F positions have E type, where C, D, F transport the relevant ingredients to the relevant smokers. C', D', F' positions give ingredients to the agent again, so the cycle is repeated. On the top of the position we put the first mark, which means the net is initialized. If on the top of the position there is the "-" sign, it means that the position is empty or it contains no token. The type is marked in italic letters below the position. The ct  position is connected to T transition. It allows to make T transition 3 times during per cycle. S, P, M positions respectively have U, N, Q types. They present the state of the 3 smokers who respectively own tobacco, paper and matches. T4 transition will be occur only if all 3 smokers finished smoking.

Now we will describe the net performance. T will occur the first transition, as there is the corresponding marks in A and ct positions. After T firing transition we check if , token is for C position and the other two (D, F) positions do not get any marks. If  then T1 transition can be occur, which describes the process of the first smoker, and  ingredients give C' position. It may occur T transition in this condition, which will move (t, m), or tokens and T2, or T3 transitions will be occur. If T1, T2, T3 transitions are occur, or the agent has proposed the 3 types of ingredients and the 3 smokers have finished smoking, then the T4transition will be occur, the agent will offer 3 types of ingredients again and the cycle will be repeated.

If we try to present this problem with Classical Petri Net, then we need to use 3 transitions instead of T transition. That also means the minimization problem of the net is also solved, which implies cost reduction due to the reduction of arcs in positions and transitions.

3. Conclusion

In the Work, we identify certain advantages of Colored Petri Net P and V operations and Classical Petri Net with the synchronization problem. The mentioned studies allow identification of synchronization modeling opportunities with the help of Colored Petri Net.

Declaration

Color ;

Color ;

Color ;

Color ;

Color ;

;

;

References

1. Peterson, James Lyle (1981). Petri Net Theory and the Modelling of Systems. Prentice Hall. ISBN 0-13-661983-5.
2. Tadao Murata. "Petri nets: Properties, Analysis and Applications." Proc. of the IEEE, 77(4), 1989.
3. K. Jensen and G. Rozenberg, Eds., High-Level Petri Nets. Theory and Application, Springer-Verlag, Berlin, 1991, pp. 44-122.
4. K. Jensen. Coloured Petri Nets: Basic Concepts, Analysis Methods and Practical Use. Springer - Verlag, Berlin, 1992.
5. Jensen K. Coloured Petri Nets: Basic Concepts, Analysis Methods and Practical Use. Springer, 1996. Vol. 1–3.
6. Jensen K, "Coloured Petri Nets: Basic Concepts, Analysis Methods and Practical Use", Basic Concepts. Monographs in Theoretical Computer Science, Springer – Verlag, Berlin, Germany, V.1,2, 3, 1997.
7. J. D. Ullman, "Elements of ML Programming," Prentice- Hall, Upper Saddle River, 1998.
8. Reising W., Rozenberg G. (eds). Lecture Notes on Petri Nets. Parts I and II // Lecture Notes in Computer Sciences. V. 1491 – 1492. Springer – Verlag, 1998.
9. K. Jensen and L.M. Kristensen. Coloured Petri Nets - Modeling and Validation of Concurrent Systems. Springer-Verlag Berlin, 2009.
10. Goharik R. Petrosyan, Andrey M. Avetisyan, Lilit A. Ter-Vardanyan Interrelation of Languages of Colored Petri Nets and Some Traditional Languages // Open Journal of Modelling and Simulation Vol.1 No.3, Pub. Date: July 11, 2013.