Numerical Study of Convective Flow in a Prismatic Cavity Using Water-Based Nanofluids
K. F. U. Ahmed*, R. Nasrin
Department of Mathematics, Bangladesh University of Engineering & Technology, Dhaka, Bangladesh
Abstract
The effect of solid volume fraction on convective flow inside a prismatic cavity is analyzed numerically. The water-based Cu and CuO nanofluids are used as the working fluids inside the cavity. This work investigates the comparative performance between these two nanofluids. The governing differential equations with boundary conditions are solved by Finite Element Method using Galerkin’s weighted residual scheme. The behavior of parameter related to performance such as temperature, velocity distributions, convective heat transfer, mean bulk temperature and magnitude of subdomain mean velocity areexamined systematically. This parameter includes the solid volume fraction f. The results show that the performance of the cavity can be improved by using the largest f. Higher heat transfer rate is obtained using water/Cu nanofluid. Magnitude of mean velocity becomes superior for water/CuO nanofluid than water/Cu nanofluid.
Keywords
Convective Flow, Streamline, Isothermal Line, Prismatic Cavity, Finite element Method, Nanofluid
Received:July 18, 2016
Accepted: August 1, 2016
Published online: August 25, 2016
@ 2016 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY license. http://creativecommons.org/licenses/by/4.0/
1. Introduction
The fluids with solid-sized nanoparticles suspended in them are called "nanofluids". Nanofluid is made by adding nanoparticles and a surfactant into a base fluid can greatly enhance thermal conductivity and convective heat transfer. The diameters of nanoparticles are usually less than 100 nm which improves their suspension properties. Nanofluid technology has emerged as a new enhanced heat transfer technique in recent years. The natural convection in enclosures continues to be a very active area of research during the past few decades. Applications of nanoparticles in thermal field are toenhance heat transfer from solar collectors to storage tanks, to improve efficiency of coolants in transformers. In view of various applications of thermal processes, a comprehensive understanding of heat transfer and flow circulations within prismatic cavities is very much essential for industrial development. Current work attempts to compare heat transfer and energy distribution between water/Cu and water/CuO nanofluids as heat transfer medium inside a prismatic cavity.
Natural convection in enclosed cavities is important in many engineering applications, for instance, geophysics, geothermal reservoirs, insulation of building, heat exchanger design, building structure and so on. These applications motivate many researchers to perform numerical simulation for investigating the flow pattern, temperature distribution and heat flow.
The steady natural convection flow in a prismatic enclosure with strip heater on bottom wall is studied and analyzed numerically by Yaseen [1]. For this enclosure, top inclined walls are considered at low temperature, two vertical walls were adiabatic and strip heater was at constant high temperature mounted on the bottom enclosure while the reminder bottom wall was kept at low temperature. However, a comprehensive analysis on heat flow during natural convection in a prismatic enclosure with the heatline approach is yet to appear in the literature. Recently, Ahmed et al. [2] have studiedand numerically analyzed natural convection flows within prismatic enclosures based on heatline approach.
Literature reviews on natural convection inside triangular, trapezoidal and rhombic enclosures having different temperature boundary conditions and filled with porous medium are available in [3-6]. The wide range of applicability of flow inside various cavities (food processing industries, molten metal industries, etc.) requires thorough understanding for cost efficient processes. Numerical analysis of heat-mass transfer through a tabular reactor is analyzed by Nasrin [7-8]. It is essential to study the heat transfer characteristics in complex geometries to obtain optimal design of the processes for improving the product quality. Natural convective heat transfer in different cavity containing a heated obstacle filled with nanofluid is studied and analyzed by Nasrin and co-authors [9-11].
Applications of natural convection flow of water-alumina nanofluid in an annulus have studied by Parvin et al. [12]. In this paper, authors found significant heat transfer enhancement due to the presence of nanoparticles and it was emphasized by increasing the nanoparticles volume fraction and Prandtl number as well as large Grashof number. Thermal characteristics of water and nanofluids (Cu–water, TiO2–water and alumina–water) confined within square cavity with various heating patterns of walls were studied by Basak and Chamkha [13]. In this paper, numerical investigations on heating characteristics within square cavities have been carried out basedon coupled partial differential equations of momentum and energy. Natural convection in a horizontal cylinder filled with water-based alumina nanofluid is numerically investigated by Meng and Li [14]. In this paper, authors found that average natural Nusselt numbers of water and Al2O3/water nanofluids increases with the Rayleigh number.
Various problems relating natural convection in partially heated enclosures for different boundary conditions in air and water-filled enclosure have been studied extensively by many researchers [15-17]. Mixed convection heat transfer and fluid flow fields inside a lid-driven cavity were studied numerically by Ismael and Chamkha [18]. Numerical analysis of mixed convection within a trapezoidal cavity with the side wall representing the moving lid in both aiding and opposing flow modes has been studied extensively. De Val Davis [19] obtained a benchmark numerical solution of buoyancy driven flow in a square cavity with vertical walls at different temperatures and adiabatic horizontal walls. De Val Davis and Jones [20] presented a comparative study on different contributed solutions to the same problem. These solutions covered the range of Rayleigh numbers from 103 to 106. The effects of vertical parabolic walls on natural convection in a parabolic enclosure have investigated numerically by Mustafa [21]. Diaz and Winston [22] have analyzed the interaction of natural convection and surface radiation in two-dimensional parabolic cavities heated from below with insulated walls and flat top and bottom walls numerically.
To study the effectiveness of the free convection in a cavity using nanofluids by increasing the rate of heat transfer the theoretical prediction in this article is hoped to be a useful guide for the experimentalists. The main issue discussed in this paper is to compare flow and heat transfer characteristics between water-Cu and water/CuO nanofluids with the variation of solid volume fraction (f) in the cavity.
2. Mathematical Formulation
The physical domain is shown in Fig. 1. The steady laminar incompressible free convective fluid flow is accounted in the current investigation. The gravitational force works in the opposite of y-direction. Constant physical and thermal characteristics of the fluid are used. The Boussinesq approximation is valid. The flow is governed by the following equations of conservation of mass, momentum and energy:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
Relationships between properties of nanofluid (nf), pure fluid (f) and pure solid (s) are given by
• Density: ![]()
• Heat capacitance: ![]()
• Thermal expansion coefficient: ![]()
• Thermal diffusivity: ![]()
• In the current study, the viscosity of the nanofluid is considered by the Pak and Cho correlation [23]. This correlation is given as ![]()
The effective thermal conductivity of the nanofluid is approximated by the Maxwell-Garnett model [24] as ![]()
The following dimensionless dependent and independent variables are used to make the equations (1) through (4) non-dimensional:
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() (5)
(5)
After substitution, the dimensionless equations are as follows:
![]() (6)
(6)
![]() (7)
(7)
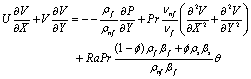 (8)
(8)
![]() (9)
(9)
In equation (5), X and Y are the dimensionless distances along x- and y-coordinate, respectively, L is vertical depth of the cavity, i.e. perpendicular distance from the bottom wall to the top corner point, U and V are the corresponding velocity components along the coordinate axes, P denotes the dimensionless pressure whereas Pr and Ra denote Prandtl and Rayleigh numbers, respectively.
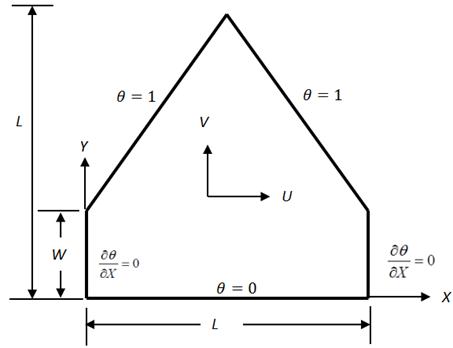
Fig. 1. Schematic diagram of the physical system.
The boundary conditions can be summarized by the following equations:
• For the bottom wall: ![]()
![]()
![]()
• For the side walls: ![]()
![]()
![]()
• For the inclined walls: ![]()
![]()
![]()
Analysis of fluid motion is displayed by means of streamfunction![]() which is obtained from velocity components U and V. The relationships between streamfunctionand velocity components for two-dimensional flows are
which is obtained from velocity components U and V. The relationships between streamfunctionand velocity components for two-dimensional flows are
![]() and
and![]() (10)
(10)
which give a single equation
![]() (11)
(11)
The positive sign of ![]() denotes anticlockwise circulation and the clockwise circulation is represented by the negative sign of
denotes anticlockwise circulation and the clockwise circulation is represented by the negative sign of ![]() The no-slip condition is valid at all boundaries as there is no cross-flow. Hence
The no-slip condition is valid at all boundaries as there is no cross-flow. Hence ![]() is used for boundaries.
is used for boundaries.
The average Nusselt number, average temperature and average velocity may be expressed as
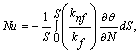
![]() and
and![]()
Where  S is the dimensionless periphery, N is the normal coordinate along the boundary and
S is the dimensionless periphery, N is the normal coordinate along the boundary and ![]() is the volume to be accounted.
is the volume to be accounted.
3. Numerical Implementation
The Galerkin finite element method (Taylor and Hood [25] and Dechaumphai [26]) is used to solve the non-dimensional governing equations along with boundary conditions for the considered problem. The equation of continuity has been used as a constraint due to mass conservation and this restriction may be used to find the pressure distribution. The finite element method of Reddy [27] is used to solve the Eqns. (6) - (9) where the pressure P is eliminated by a constraint. The continuity equation is automatically fulfilled for large values of this penalty constraint. Then the velocity components (U, V) and temperature (θ) are expanded using a basis set. The Galerkin finite element technique yields the subsequent nonlinear residual equations. Three points Gaussian quadrature is used to evaluate the integrals in these equations. The non-linear residual equations are solved using Newton–Raphson method to determine the coefficients of the expansions. The convergence of solutions is assumed when the relative error for each variable between consecutive iterations is recorded below the convergence criterion ε such that ![]() , where n is the number of iteration and
, where n is the number of iteration and![]() is a function of U, V and θ.
is a function of U, V and θ.
3.1. Mesh Generation
In the finite element method, the mesh generation is the technique to subdivide a domain into a set of sub-domains, called finite elements, control volume, etc. The discrete locations are defined by the numerical grid, at which the variables are to be calculated. It is basically a discrete representation of the geometric domain on which the problem is to be solved. The computational domains with irregular geometries by a collection of finite elements make the method a valuable practical tool for the solution of boundary valueproblems arising in various fields of engineering. Fig. 2 displays the finite element mesh of the present physical domain.
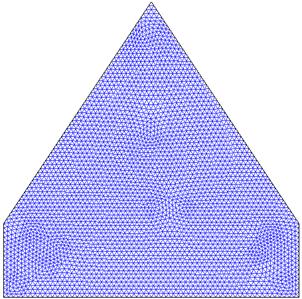
Fig. 2. Finite element meshing of the computational domain.
3.2. Grid Independent Check
An extensive mesh testing procedure is conducted to guarantee a grid-independent solution for Ra = 104 and Pr = 0.7 in a prismatic enclosure. In the present work, five different non-uniform grid systems are examined with the following number of elements within the resolution field: 454, 926, 1504, 2270 and 9948. The numerical scheme is carried out for highly precise key in the average Nusselt (Nu) number for the aforesaid elements to develop an understanding of the grid fineness as shown in Fig. 3. The scale of the average Nusselt numbers for 2270 elements shows a little difference with the results obtained for the other elements. Hence, considering the non-uniform grid system of 2270 elements is preferred for the computation.
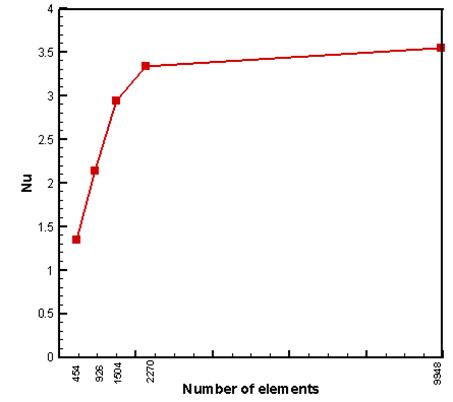
Fig. 3. Grid independent check.
3.3. Thermo-Physical Properties
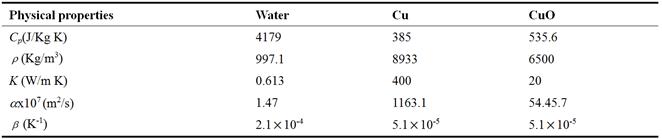
The thermo-physical properties of fluid (water), solid Cu and CuO are tabulated in Table 1. The properties are taken from Nasrin and Alim [28].
Table 1. Thermo-physical properties of water/Cu and water/CuO nanofluids at 300K.
4. Results and Discussion
Numerical results in terms of isotherms and streamlines are displayed for various solid volume fraction f (= 0%, 1%, 2% and 3%) while Prandtl number Pr = 5.8 and Rayleigh number Ra = 104 are kept fixed. In addition, the values of the average Nusselt number on both hot and cold walls, mean bulk temperature, magnitude of subdomain mean velocity inside the cavity have been calculated for water/Cu and water/CuO nanofluids. In the following, the performances of two nanofluids are compared in terms of streamlines, isotherms, heat transfer rate and velocity profiles.
4.1. Effect of Solid Volume Fraction on Isotherms
Fig. 4 (a-b) demonstrates the effect of different solid volume fraction f (= 0%, 1%, 2% and 3%) using water/Cu and water/CuO nanofluids on isothermal lines.The red and blue colors of the isothermal lines represent the highest and lowest temperatures respectively. For all theconsidered values of f, the pattern of isotherms are smooth and monotonic and they are symmetric to the central vertical line. The higher temperature lines remain near the hot upper walls at f = 0%. With the increasing value of f from 0% to 3%, these lines move toward the bottom wall. Most of the isothermal lines become almost horizontal straight line pattern. The higher temperatures isothermal lines become less bended and have parabolic form. This happens due to the presence of nanoparticle in the fluid which causes higher temperature gradient and so the isothermal lines move from the hot wall to the cold wall. For the other values of solid volume fraction f (= 1% and 2%), water/Cu nanofluid has no apparently different temperature gradient with water/CuO nanofluid. It is found that using 3% solid volume fraction water/Cu nanofluid has higher temperature gradient compared to that of water/CuO nanofluid. Thus, higher heat transfer rate is obtained using water/Cu nanofluid at f = 3%.
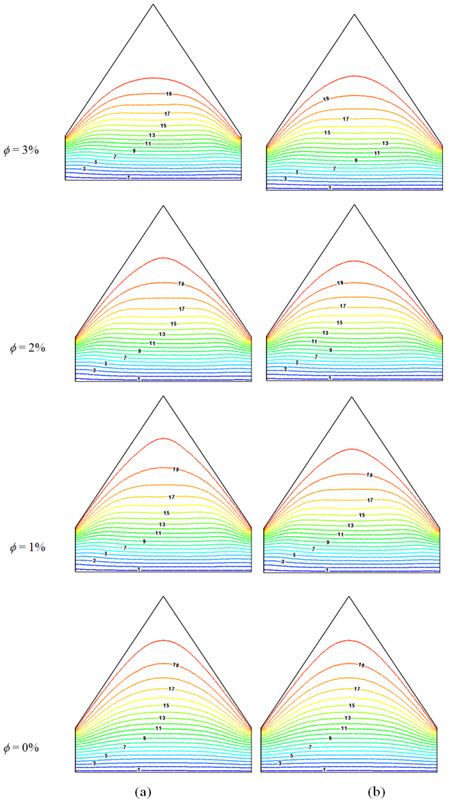
Fig. 4. Effect of f on isothermal lines using (a) water/Cu and (b) water/CuO nanofluids
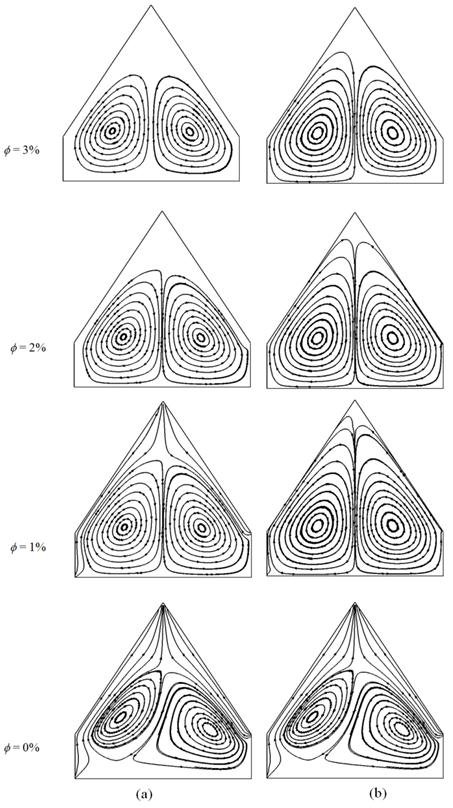
Fig. 5. Effect of f on streamlines using (a) water/Cu and (b) water/CuO nanofluids.
4.2. Effect of Solid Volume Fraction on Streamlines
Fig. 5 (a-b) shows the effect of different solid volume fraction f on streamlines using water/Cu and water/CuO nanofluids. Initially, using water as heat transfer medium the circulation cells inside the enclosure are completely different but eventually they become symmetric along vertical when water/Cu nanofluid is used. Qualitatively similar trends in streamlines are observed for the usage of water/CuO nanofluid. With the increasing values of f, the streamlines are less dense near the central vertical line. The circulatory streamlines are moving from the side walls to the centre of the vortices. The shape of core cells is changed from horizontal to vertical format for variation of solid concentration f using both nanofluids.
4.3. Average Nusselt Number
The distribution of the average Nusselt number at the top inclined walls and bottom wall, respectively, versus the solid volume fraction of nanofluidsare shown in Fig. 6(a-b). The mean Nusselt number for water/Cu and water/CuO nanofluids increases with rising values of solid volume fraction and it is utilized to represent the overall heat transfer rate within the domain. It is seen that the average Nusselt number enhances slowly upto f = 1% and beyond this region they rise rapidly for the values of different concentration of water/Cu and water/CuO nanofluids. Similar trend of heat transfer is seen for both the walls. Highest heat transfer rate is observed for f = 3%. For inclined walls, the rate of heat transfer increases by 20% for water/Cu, 13% for water/CuO and for bottom wall it is 19% for water/Cu and 12% for water/CuO respectively with the variation of f.
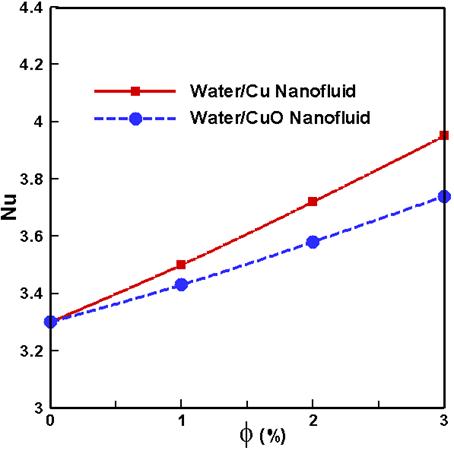
(a)

(b)
Fig. 6. Average Nusselt number at the (a) top inclined walls and (b) bottom wall.
4.4. Average Bulk Temperature
Fig. 7 demonstrates the distribution of average bulk temperature inside the cavity versus the solid volume fraction f from 0% to 3%. It is observed that the mean bulk temperature of both type of nanofluids rise with the increase of the parameter f. It is well known that higher concentration of solid particle enhances thermal conductivity as well as temperature of the working nanofluid. The performance of water/Cu nanofluid is found to be higher than that of water/CuO nanofluid.
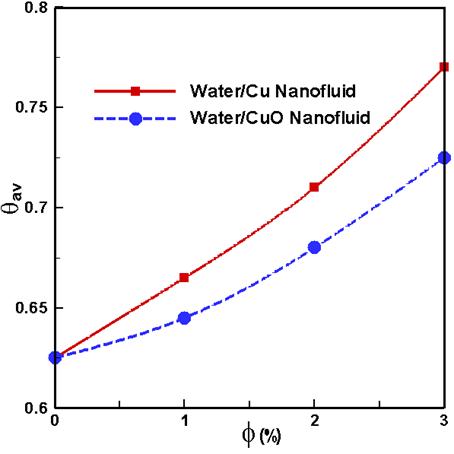
Fig. 7. Average bulk temperature inside the cavity.
4.5. Mean Subdomain Velocity
The magnitude of mean velocity in the computational domain is depicted in Fig. 8. In this velocity profile, the effect of solid concentration f (= 0%-3%) of water-based nanofluids show the opposite behavior compared to the other profiles. Growing f devalues magnitude of mean velocity of both nanofluids. This happens because solid concentrated nanofluid cannot move freely like clear water. It is observed that the magnitude of mean subdomain velocity of water/Cu nanofluid is lower than that of water/CuO nanofluid. The fact is that density of Cu nanoparticle is higher than that of CuO nanoparticle.
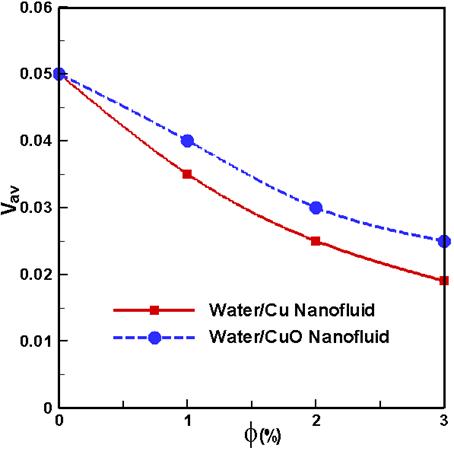
Fig. 8. Subdomain mean velocity in the cavity.
5. Conclusion
A numerical study has been performed to investigate the comparative effects of water/Cu and water/CuO nanofluids on natural convection flow field. The behavior of parameter related to performance such as temperature, velocity distributions, convective heat transfer and magnitude of subdomain mean velocity are examined. Solid volume fraction f is the key controlling parameter for this analysis which governs the overall heat transfer rate, i.e. mean Nusselt number. With average Nusselt number of water-based nanofluids at the top inclined walls and the bottom wall of the prismatic enclosure enhancement of heat transfer rate has been illustrated via isotherms associated with trajectory of heat flow. Different values of solid volume fraction have been chosen such that the system depicts a wide range of commonly used applications. Convective heat transfer is found to be dominant for water-based nanofluids. It is interesting to observe that using water/Cu nanofluid the heat transfer rate is found to be higher and the magnitude of mean velocity becomes superior for water/CuO nanofluid than water/Cu nanofluid. So the overall heat transfer performance inside the prismatic cavity is better using water/Cu nanofluid than water/CuO nanofluid.
Nomenclature
| Cp | specific heat at constant pressure [Jkg-1K-1] |
| g | Gravitationalacceleration [ms-2] |
| k | thermal conductivity [Wm-1K-1] |
| L | length of the base and height of the prismatic cavity [m] |
| Nu | Nusselt number |
| p | dimensional pressure [Nm-2] |
| P | dimensionless pressure |
| Pr | Prandtl number |
| Ra | Rayleigh number |
| T | dimensional temperature [K] |
| u | x-component of velocity [ms-1] |
| U | x-component of dimensionless velocity |
| v | y-component of velocity [ms-1] |
| V | y-component of dimensionless velocity |
| x | distance along x-coordinate [m] |
| X | dimensionless distance along x-coordinate |
| y | distance along y-coordinate [m] |
| Y | dimensionless distance along y-coordinate |
Greek Symbols
| α | thermal diffusivity [m2s-1] |
| β | thermal expansion coefficient [K-1] |
|
| solid volume fraction |
|
| penalty parameter |
| ν | kinematic viscosity of the fluid [m2s-1] |
| θ | dimensionless temperature |
| ρ | density of the fluid [kgm-3] |
| y | stream function |
Subscripts
| av | average |
| c | cold |
| h | hot |
| f | base fluid |
| nf | nanofluid |
| s | solid particle |
References
- S.J. Yaseen, Numerical study of steady natural convection flow in a prismatic enclosure with strip heater on bottom wall using FLEXPDE, Diyala Journal of Engineering Sciences, Vol. 7 (1), pp. 61-80, 2014.
- K.F.U. Ahmed, S. Parvin and AJ. Chamkha, Numerical analysis based on heatline approach for natural convection flows within prismatic enclosures, International Journal of Energy and Technology, Vol. 7 (2), pp. 19-29, 2015.
- R. NasrinandM.A. Alim,Freeconvective flow of nanofluid having twonanoparticlesinside a complicatedcavity, International Journal of Heat and Mass Transfer, Vol. 63, pp. 191-198, 2013.
- S. Parvin, K.F.U. Ahmed, M.A. Alim and N.F. Hossain, Heat transfer enhancement by nanofluid in a cavity containing a heated obstacle, International Journal of Mechanical and Materials Engineering, Vol. 7 (2), pp. 128-135, 2012.
- R. Nasrin, S. Parvin, M.A. Alim and A.J. Chamkha, Non-darcy forced convection through a wavy porous channel using CuO nanofluid, International Journal of Energy and Technology, Vol. 4 (8), pp. 1-8, 2012.
- R. Nasrin and S. Parvin, Investigation of buoyancy-driven flow and heat transfer in a trapezoidal cavity filled with water-Cu nanofluid, International Communications in Heat and Mass Transfer, Vol. 39 (1), pp. 270-274, 2012.
- R. Nasrin, Numerical analysis through a tubular reactor: velocity effect, International Journal of Heat and Technology, Vol. 34 (1), pp. 57-64, 2016.
- R. Nasrin,Heat-mass transfer in a tubular chemical reactor, International Journal of Energy Science and Engineering, Vol. 1 (2), pp. 49-59, 2015.
- S. Parvin, R. Nasrin and M.A. Alim, Heat transfer performance of nanofluid inacomplicatedcavitydue to Prandtl number variation, Procedia Engineering, Vol. 90, pp. 377-382, 2014.
- R. Nasrin, S. Parvin and M.A. Alim, Entropy generation inside a narrow channel with thermal radiation, International Journal of Energy and Technology, Vol. 6 (27), pp. 1-9, 2014.
- R. Nasrin,M.A. Alim and A.J. Chamkha, Temperature dependent thermal conductivity and viscosity of nanofluid, International Journal of Energy and Technology, Vol. 6 (2), pp. 1-9, 2014.
- S. Parvin, R. Nasrin, M.A. Alim, N.F. Hossain and A.J. Chamkha, Thermal conductivity variation on natural convection flow of water-alumina nanofluid in an annulus, International Journal of Heat and Mass Transfer, Vol. 55 (19-20), pp. 5268-5274, 2012.
- T. Basak and A.J. Chamkha, Heatline analysis on natural convection for nanofluids confined within square cavities with various thermal boundary conditions, International Journal of Heatand Mass Transfer, Vol. 55, pp. 5526-5543, 2012.
- X. Meng and Y. Li, Numerical study of natural convection in a horizontal cylinder filled with water-based alumina nanofluid, Nanoscale Research Letters, 10:142, 2015.
- K. B.Nasr, R. Chouikh, C. Kerkeni and A. Guizani, Numerical study of the naturalconvection in cavity heated from the lower corner and cooled from the ceiling, Applied Thermal Engineering, Vol. 26, pp. 772-775, 2006.
- Y. Varol, A. Koca and H.F. Oztop, Natural convection in a triangle enclosure withflush mounted heater on the wall,InternationalCommunications in Heat and Mass Transfer, Vol. 33, pp. 951-958, 2006.
- A.Koca, H.F. Oztop and Y. Varol, The effects of Prandtl number on natural convection in triangular enclosures with localized heating from below,InternationalCommunications in Heat and Mass Transfer, Vol.34, pp. 511-519, 2007.
- M.A. Ismael and A.J. Chamkha, Mixed convection in lid-driven trapezoidal cavities with an aiding or opposing side wall, Numerical Heat Transfer, Part A, Vol. 68 (3), pp. 312-335, 2015.
- G. De Vahl Davis, Natural convection of air in a square cavity: a bench mark numerical solution, International Journal of Numerical Methods in Fluids, Vol. 3, pp. 249-264, 1983.
- G. De Vahl Davis and I.P. Jones, Natural convection in a square cavity: a comparison exercise, International Journal of Numerical Methods in Fluids, Vol. 3, pp. 227-248, 1983.
- A.W. Mustafa, Natural convection in parabolic enclosures heated from below, Modern Applied Science, Vol. 5 (3), pp. 213-220, 2011.
- G. Diaz and R. Winston, Effect of surface radiation on natural convection in parabolic enclosure, Numerical Heat Transfer, Part A, Vol. 53, pp. 891-906, 2008.
- B.C. Pak andY. Cho, Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particle, Experimental Heat Transfer, Vol. 11, pp. 151-170, 1998.
- J.C. Maxwell-Garnett,Colours in metal glasses and in metallic films,Philosophical Transactions of the Royal Society A,Vol. 203, pp. 385-420,1904.
- C. Taylor and P. Hood, A numerical solution of the Navier-Stokes equations using finite element technique, Computer and Fluids, Vol. 1, pp. 73-89, 1973.
- P. Dechaumphai, Finite element method in engineering. 2nd edition, Chulalongkorn University Press, Bangkok, 1999.
- J.N. Reddy and D.K. Gartling, The finite element method in heat transfer and fluid dynamics, CRC Press, Inc., Boca Raton, Florida, 1994.
- R. Nasrin and M.A. Alim, Performance of nanofluids on heat transfer in a wavy solar collector, International Journal of Engineering Science and Technology, Vol. 5 (3), pp. 58-77, 2013.



