The Symmetries of Solutions of Partial Differential Equations

Rufina Abdullina^*, Alena Agafonova

Department of Physics and Mathematics, Sterlitamak Branch of the Bashkir State University, Sterlitamak, Russia

Abstract

The first general solution of the problem of Сaushy for an extensive class of partial differential equations was given by Riemann almost a century ago in his well-known paper on the propagation of sound waves of finite amplitude. Although stated only for certain special equations, it is applicable to any linear equation of hyperbolic type of the second order in two independent variables; it depends ultimately on finding a certain subsidiary function, often called the Riemann function, which is the solution of a characteristic boundary value problem for the adjoint equation. This paper is of a synthetic nature, being a result of combining Riemann’s method for integrating second-order linear hyperbolic equations with Lie’s classification of such equations. In paper was found the solution of the Cauchy problem by the Riemann method for a hyperbolic equation. It was also shown the invariance of the Riemann function relatively to the symmetry of the fundamental solutions.

Keywords

Problem Cauchy, Riemann’s Function, Hyperbolic Equation, Group Analysis

Received:May 23, 2016
Accepted: August 1, 2016
Published online: August 19, 2016

@ 2016 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY license. http://creativecommons.org/licenses/by/4.0/

1. Introduction

Group analysis of differential equations is widely used in the study of equations of mathematical physics. Recent advances and applications of group analysis are reflected in monographs [1-6]. The most widely used are invariant with respect to the subgroup of permissible solutions group transformations. In [7] in relation to the private hyperbolic equation of second order with two independent variables Riemann proposed a "Riemann method of integration" which received extensive development in the future [8,9]. For use this method it is need to build the so-called Riemann function. General method of construction of the Riemann function does not exist. In [10] in relation to the private hyperbolic equation of second order with two independent variables Riemann proposed a "Riemann method of integration" which received extensive development in the future [8,9]. For use this method it is need to build the so-called Riemann function. General method of construction of the Riemann function does not exist. This paper is of a synthetic nature, being a result of combining Riemann’s method [11] for integrating second-order linear hyperbolic equations with Lie’s classification [12] of such equations. One can find in [13] a detailed description of known methods of constructing Riemann’s function (called in [14] the Riemann–Green function) for particular types of equations. Specifically, six methods are described there. So far as I know, six ways have been used to find the Riemann-Green function for particular types of hyperbolic equations. These will be discussed in the following order.

(i) Riemann’s original method was based on the fact that the Riemann-Green function does not defend in any way on the curve carrying the Cauchy data. If it is possible to solve by some other means the Problem of Cauchy for a special curve C depending on one variable parameter, a comparison of the two solutions should give the Riemann-Green function. In the case of the two equations considered by Riemann, it was possible to solve the Problem of Cauchy by a Fourier cosine transform with Cauchy data on a straight line.

(ii) Hadamard pointed out that the coefficient of the logarithmic term in his elementary solution is the Riemann-Green function of the adjoint equation. It is possible to modify Hadamard’s construction so as to give both functions at the same time.

(iii) It is easy to construct an integral equation whose unique solution is the Riemann-Green function.

(iv) Chaudy, in his work on partial differential equations of hypergeometric type, was able to construct the Riemann-Green function by the use of symbolic operators and power series. This work appears to be little known.

(v) A. G. Mackie has constructed complex integral solutions of certain equations. Such a complex integral gives the Riemann-Green function for an appropriate choice of contour. To some extent, Mackie was anticipated by Chaudy, whose approach was rather different.

2. Main Results

Сonsider the following hyperbolic equation of the second order:

              (1)

in an open domain , which is bounded by curves of  (),  () and with the section  ().

Let’s pose the problem of Cauchy: Find in the domain  function , satisfying the conditions

          (2)

                      (3)

       (4)

where − given sufficiently smooth functions.

With the help of the change of variables ,  equation (1) leads to the canonical form:

                         (5)

To solve the problem we use the method of Riemann, which is based on the following identity:

 (6)

where

,    (7)

− adjoint with  differential operator;  − domain of integration with piecewise-smooth contour Γ.

Integrating both sides of (6) in the domain of and, using the formula of Ostrogradsky, obtain

Riemann’s method reduces the problem of integrating the equation (1) to construct an auxiliary Riemann’s functio, that satisfies the homogeneous adjoint equation (the variables ):

and the following conditions on the characteristics of:

,

,                           (8)

.

The Riemann’s formula in general is for the solution of equation (7) has the form

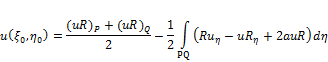
where the double integral is taken over the domain bounded by the characteristics , and the curve γ (PQ). The solution of the Goursat problem (8) is unique.

The group-theoretical approach presented below provides the seventh method. Using the results for the group classification of homogeneous hyperbolic equation of the second order, it was suggested to find a function of Riemann using the symmetries of the equation. Let us demonstrate this with a following examples.

Example 1. The telegraph equation

                                  (9)

is one of the simplest equations to which Riemann’s method

is applicable. In this case, the Goursat problem has the form

Usually, textbooks offer the following "method" for solving it: let us look for a solution of the problem (9) in the form

                (10)

This leads to the ordinary differential equation

which is Bessel’s equation and assumes the standard form

upon the substitution  Thus the Riemann function for the telegraph equation (9) is expressed in terms of Bessel’s function  in the form

On the other hand the telegraph equation (9) admits the three-parameter group with the generators

Let us find a linear combination of these operators

,

admitted by the Goursat problem (9). Let us require first the invariance of the characteristics , . The invariance test has the form

It follows that , since otherwise α = β = 0. Therefore one can set γ = 1 and obtain , . One can readily verify that the resulting operator

          (11)

is admitted by the Goursat problem (9). Therefore one can use the invariance principle and look for the solution to the Goursat problem among invariant functions with respect to the one-parameter group with the generator (11). This group has two independent invariants, namely v and . Therefore the invariant solution has the form (10).

Example 2. Riemann himself applied the method he suggested to the following equation

For this equation the conditions (8) on the characteristics are written

Riemann reduces the resulting characteristic Cauchy problem to an ordinary differential equation (which defines a special Gauss’ hypergeometric function) by assuming that v is a function of the one variable

Equation also admits three operators, namely:

As in the previous example, one can find uniquely this linear combination

leaving invariant the characteristics and the conditions on the characteristics. Therefore we shall look for the solution of the problem in the class of invariant functions. Since the invariants for the operator X are v and

the invariant solution has the form v = v(µ).

This is the invariant solution found by Riemann; the variable z he used is related to the invariant µ by the functional relation z = µ/(1 − µ), and hence is also an invariant.

In our case, the equation adjoint equation (5) has the form

                      (12)

The function of Riemann , Let’s note that in our case the desired function of Riemann satisfies the following conditions on the characteristics:

.     (13)

The symmetry operator of the homogeneous equation (12) has the form [4]:

Thus, as follows from [5], must be done the following relations:

Substituting in this case , , , we’ll obtain the following relations

where − arbitrary constants. We write out a finite part of the basis of the Lie algebra of symmetry operators of the equation (5):

Let’s construct a linear combination of these operators

,

where − arbitrary constants.

Following [6], we require invariance characteristics  and  regarding construction of the operators:

If we choose , we’ll get , . Then the resulting operator takes the form

Invariants of this operator have the form

therefore we’ll seek the solution of equation (5) as a function of  where  As a result of substitution of R in equation (12), it splits into two ordinary differential equations

The solutions of the obtained equations are functions

where − Besel’s function of the first kind of order zero,  − an arbitrary constant.

Then satisfied with the decisionof the conditions (6), we obtain the Riemann’s function

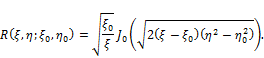
Since , then

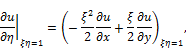
and

Substituting in the formula (9) , ,  and, taking into account, that

we’ll get

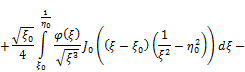
Returning to the old variables x and y, we’ll get the solution of the Cauchy’s problem

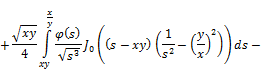
 (14)

Theorem. If the functions , then the Cauchy’s problem for equation (1) has a unique solution, which is defined by (14).

As in first case, the theorem is proved by direct verification that the formula (8) is a solution of equation (6).

3. Conclusions

We formulate an algorithm for constructing the Riemann function through the use of symmetries of the fundamental solutions:

1. Finding symmetries of linear equation (1).

2. Construction of invariant solutions with symmetries of the fundamental solutions.

3. Isolation of the Riemann function of invariant solutions found by using the Riemann function continuity condition and its first derivatives at the point  and the condition that .

This algorithm allows to find the Riemann function hyperbolic equations without characteristic variables. This underlines the invariant nature of this method of construction of the Riemann function.

Acknowledgments

My sincere thanks go to Prof. Andrey Akimov from the Sterlitamak Branch of the Bashkir State University for his help and advice.

References

1. CRC Handbook of Lie Group Analysis of Differential Equations. Editedby N.H. Ibragimov. CRC Press. USA:Vol. 1. Symmetries, exact solutions, and conservation laws. 1994. 429 p.Vol. 2. Applications in engineering and physical sciences. 1995. 546 p.Vol. 3.New trends in theoretical developments and computational methods. 1996. 536 p.
2. Ibragimov N.H. Elementary Lie Group Analysis and Ordinary Differential Equations. John Wiley & Sons Ltd. Great Britain. 1999. 347 p.
3. Bluman G.W., Anco St.C. Symmetry and Integration Methods for Differential Equations. Springer–Verlag New York, Inc. 2002. 419 p. (Applied Mathematical Sciences. Vol. 154).
4. Cantwell Br. J.Introduction to Symmetry Analysis. Cambridge. Cambridge University Press. 2002. 654 p.
5. Euler N., Steeb W.–H. Continuous Symmetries, Lie Algebras and Differential equations. Leipzig. Wissenschaftsverlag. 1992. 320 p.
6. R. Gorenfloand S. Vessella, Abel integral Equations: Analysis and Application, Springer-Verlag, Berlin-NewYork, 1991.
7. Jerri A. Introduction to Integral Equations with Applications. Wiley, NewYork, 1999.
8. Davis H.T. Introduction to Nonlinear Differential and Integral Equations, 1sted., Dover Publications, Inc., NewYork,1962.
9. Manzhirov A. V. and PolyaninA.D.Handbook of Integral Equations: Solution Methods [in Russian], Factorial Press, Moscow, 2000.
10. Deutsch M., Beniaminy I. Derivative-free Inversion of Abel’s Integral Equation. Applied Physics Letters 41: pp. 27-28, 1982.
11. Anderssen R.S. Stable Procedures for the Inversion of Abel’s Equation. Journal of the Institute of Mathematics and its Applications 17: pp. 329-342, 1976.
12. Minnerbo G. N., Levy M. E. Inversion of Abel’s Integral Equation by Means of Orthogonal Polynomials. SIAM Journalon Numerical Analysis 6: pp. 598-616, 1969.
13. J. D. Tamarkin, "On integrable solutions of Abel’s integral equation," Annals of Mathematics, vol. 31, no. 2, pp. 219–229, 1930.
14. A. C. Pipkin, A Courseon Integral Equations, Springer–Verlag, NewYork, 1991.
15. Akimov A., Galiaskarova G. The solution of the Darboux problem for the telegrath equation with deviation from the characteristic, International Journal of Pure and Applied Mathematics. 2015. Т. 103. № 2. С. 377-383.
16. R. Naz and F. M. Mahomed "Dynamic Euler-Bernoulli Beam Equation: Classification and Reductions", Hindawi Publishing Corporation Mathematical Problems in Engineering, Volume 2015(2015).