TG Index and Its Application on Alkanes and Alkenes
Selcuk Gumus1, *, Lemi Turker2
1Yuzuncu Yıl University, Faculty of Sciences, Department of Chemistry, Kampus, Van, Turkey
2Middle East Technical University, Faculty of Arts and Sciences, Department of Chemistry, Ankara, Turkey
Abstract
Topological indices have an important role in chemical graph theory. Description of chemical structure with a number provides being able to guess unmeasured properties of known and unknown compounds. (Turker-Gumus Index) TG Index has been described and its application on some physical properties of alkanes and alkenes have been reported. The TG Index is a novel index based on connectivity and distances in the graph of a molecular structure. The authors have tried to use TG index to model some important properties in alkanes and alkenes. The index is very well correlated with the applied properties with only a few exceptions.
Keywords
TG Index, Topological Indices, T(A) Graphs, Alkanes, Alkenes
Received: April 9, 2015 / Accepted: April 17, 2015 / Published online: May 8, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
Topological indices are numbers associated with constitutional formulas by mathematical operations on the graphs representing these formulas. The necessity of having to use such tools as topological indices originates in the fact that physico-chemical properties are expressed as numbers and thus have a metric enabling scientists to make comparisons and correlations. In order to evaluate quantitatively the degree of similarity or dissimilarity of chemical structures or to find correlations between structures and properties (QSAR or QSPR) one needs to translate structures into numbers. For electronic factors, quantum chemistry or linear free energy relationships provide such numerical data. For steric factors or hydrophobicity/hydrophilicity there are well-established numerical data. For shape, however, topological indices provided a simple solution [1-3].
Ever since structure theory became able to explain the isomerism phenomenon and to predict what substances with a given molecular formula can exist, chemists have tried to predict the properties of these substances before they were synthesized. After some of these substances were prepared, the predictions could be checked and the prediction methods could be validated or improved [1-3].
Probably the first chemist who attempted such predictions was Kopp who published his results in 1844 [4]. His methods were primitive because the structure theory was just emerging. With the advent of quantum theory and more recently with the help of computer-assisted semiempirical or ab initio calculations, the theoretical background of molecular chemistry reached a satisfactory level for understanding chemical reactivity and for describing transition states. It was Erich Hückel who for the first time thought about applying to molecules the π-electron approximation and invented the equivalence between the eigenvalues of the adjacency matrix of a graph symbolizing the σ-electron framework and the energy levels of π-electrons in conjugated systems [5]. Thus, topological or graph theoretical data are deeply associated with the core of quantum chemistry [6].
Most of the proposed topological indices are related to either vertex adjacency relationship (connectivity) in the molecular graph or to graph theoretical (topological) distances. Therefore, the origin of topological indices can be traced either to the adjacency matrix of a molecular graph or to the distance matrix of a molecular graph. Furthermore, since the distance matrix can be generated from adjacency matrix [7], most of the topological indices are really related to the latter matrix [8].
Alkanes
Alkanes represent an attractive class of compounds as a starting point for the application of graph theoretical approaches because of their non-polar characteristics and presence of just two kinds of atoms. The use of more polar compounds is avoided due to some complexities. Moreover, many properties of alkanes change in a regular manner with their mass and the extent of branching.
The aim of this study is to investigate the possible structure-property relationships (QSPR) for the various physicochemical and electronic properties of the alkanes and alkenes. Such relationships can be employed to predict yet unmeasured values for the considered properties of compounds, in addition to that, it can be extended for design of non-existent structures possessing some desirable properties.
Since the alkanes are non-polar, a number of complexities due to polarity, polarizability, and hydrogen bonding that arise with more polar compounds are avoided. Thus, the physicochemical properties of alkanes are dominated by their inherent structural features, such as molecular dimension or shape. The molecular size has an impact and influence on most properties (activities), although other factors such as branching and steric factors also have smaller influences. In the present study, the authors are mainly concerned with the size and branching effects on some physical, physiological and electronic properties.
2. Method of Calculation
The physical properties considered in this part are boiling points (bp), molar volumes at 20 ˚C (MV), molar refractions at 20 ˚C (MR), heats of vaporization at 25 ˚C (HV), critical temperatures (TC), critical pressures (PC), surface tensions at 20 ˚C (ST), melting point (mp), molar susceptibility (χm), polarizability (α), density (d) and parachore (PR). Values for the properties were excerpted from the literature [9]. The molar volumes were calculated as MW/d where MW is the molecular weight and d is the density (g/mL). The molar refractions were calculated by using Lorentz-Lorenz expression [10] where no is the index of refraction.
![]() (1)
(1)
In the present study, MR is considered due to its relationship to molecular polarizability [11-16]. Only liquid-phase values for MV, MR, HV and ST were used. Among the branched alkanes, the TG index of 2,2-dimethyl propane cannot be calculated since the distance-degree matrix of the unstared set has only one element which leads TG index to be zero.
For the compounds considered, additional data have been gathered from the literature [17,18] for the aqueous solubilities (Sw, expressed as log Sw), as well as the partition coefficient in octanol-water solvent system (Poct, expressed as logPoct).
3. Results and Discussion
Consequent to above, unbranched alkanes were discussed, and the study was then extended to a large number of alkanes consisting of branched and unbranched structures. First, QSPR models based on boiling points (bp) were developed and then, several other properties of alkanes were considered [18].
3.1. Linear Alkanes
The correlation analyses have been performed between the natural logarithm of the TG Index and the physical properties (bp, mp, χm, α, d, PR, log Poct, log P16 and - log Sw) of the linear alkanes. The properties of the linear alkanes together with the calculated TG Index data, and the results of the regression analyses have been given in Tables 1 and 2, respectively.
The boiling point (bp) of a compound is related directly to the chemical structure of the molecules. Pioneering work in applying QSPR to the boiling points of alkanes was done by Wiener [19]. Since then, there have been very extensive efforts to apply structural information to fit experimental boiling points. Most of this work was centered at homologous and congeneric series of compounds. Here the boiling points of 17 linear alkanes (butane to eicosane) have been considered for correlation with the TG index. As can be seen from Table 2 a very good fit is obtained for these class of compounds with a coefficient of determination of 0.9919.
Table 1. Calculated TG Index values and some physical properties of the linear alkanes. (Units: bp, °C; mp, °C; χm, m3/mol; d, g/cm3; α, C·m2·V-1)
| # of C atoms | Alkane | TG | bp | mp | χm | logPoct |
| 4 | n-Butane | 9 | -0.5 | -138 | 50.3 | 3.14 |
| 5 | n-Pentane | 40 | 36.1 | -130 | 61.5 | 3.67 |
| 6 | n-Hexane | 169 | 68.7 | -95 | 74.1 | 4.21 |
| 7 | n-Heptane | 448 | 98.4 | -91 | 85.2 | 4.74 |
| 8 | n-Octane | 1156 | 125.7 | -57 | 96.6 | 5.28 |
| 9 | n-Nonane | 2400 | 150.77 | -54 | 108.1 | 5.82 |
| 10 | n-Decane | 4900 | 174.12 | -30 | 119.5 | 6.35 |
| 11 | n-Undecane | 8800 | 196.8 | -26 | 131.8 | 6.89 |
| 12 | n-Dodecane | 14641 | 216.3 | -10 | 7.42 | |
| 13 | n-Tridecane | 25480 | 235.4 | -5.5 | 7.96 | |
| 14 | n-Tetradecane | 41209 | 263.7 | 6 | 8.5 | |
| 15 | n-Pentadecane | 62720 | 270.1 | 10 | 9.03 | |
| 16 | n-Hexadecane | 97344 | 280 | 18 | 187.6 | 9.57 |
| 17 | n-Heptadecane | 137088 | 292 | 22 | 10.1 | |
| 18 | n-Octadecane | 197136 | 308 | 28 | 10.64 | |
| 19 | n-Nonadecane | 273600 | 320 | 32 | 11.18 | |
| 20 | n-Eicosane | 378225 | 342.7 | 36.8 | ||
| TG | -logSw | d | PR | α | ||
| 4 | n-Butane | 9 | 2.57 | 231 | 9.99 | |
| 5 | n-Pentane | 40 | 3.18 | 0.626 | 270.8 | 11.83 |
| 6 | n-Hexane | 169 | 3.84 | 0.659 | 310.6 | 13.66 |
| 7 | n-Heptane | 448 | 4.53 | 0.684 | 350.4 | 15.5 |
| 8 | n-Octane | 1156 | 5.24 | 0.703 | 390.2 | 17.34 |
| 9 | n-Nonane | 2400 | 5.88 | 0.718 | 430 | 19.17 |
| 10 | n-Decane | 4900 | 6.98 | 0.73 | 469.7 | 21.01 |
| 11 | n-Undecane | 8800 | 7.59 | 0.74 | 509.5 | 22.85 |
| 12 | n-Dodecane | 14641 | 7.67 | 0.749 | 549.3 | 24.28 |
| 13 | n-Tridecane | 25480 | 0.756 | 589.1 | 26.52 | |
| 14 | n-Tetradecane | 41209 | 7.96 | 0.763 | 628.9 | 28.36 |
| 15 | n-Pentadecane | 62720 | 0.769 | 668.7 | 30.19 | |
| 16 | n-Hexadecane | 97344 | 8.4 | 0.773 | 708.4 | 32.03 |
| 17 | n-Heptadecane | 137088 | 0.778 | 748.2 | 33.87 | |
| 18 | n-Octadecane | 197136 | 0.777 | 788 | 35.7 | |
| 19 | n-Nonadecane | 273600 | 0.777 | 825.8 | 37.4 | |
| 20 | n-Eicosane | 378225 | 0.789 | 1225.6 | 55.91 |
Table 2. The regression equations and the coefficients of determination of the regression analyses between the TG index and the experimental properties of linear alkanes.
| Property | regression equation | R2 |
| bp (n = 17) | y = 32.602x + 92.423 | 0.9919 |
| mp (n = 17) | y = 17.663x + 186.19 | 0.9901 |
| χm (n = 9) | y = 14.194x + 186.19 | 0.9411 |
| logPoct (n = 16) | y = 0.793x + 0.2688 | 0.9466 |
| -logSw (n = 11) | y = 0.7015x + 0.6224 | 0.9693 |
| d (n = 16) | y = 0.0169x + 0.5787 | 0.9735 |
| PR (n = 16) | y = 58.809x + 18.486 | 0.9471 |
| α (n = 16) | y = 2.7112x + 0.1828 | 0.9461 |
The boiling points of alkanes are determined by the forces of attraction between the molecules in the liquid form. Since the molecules in the solid state have a rigid three-dimensional structures, melting point unlike boiling point, is a solid state property and hence is influenced by properties of solids such as amorphous or crystalline nature, allotropy, polymorphism, molecular symmetry, as additional and more important factors than intermolecular forces. Hence, the melting points of alkanes are more difficult to model. The data in Table 2 for the regression of TG index with the melting point indicate that in spite of the complexities of solid state properties included in melting points, the TG index is very successful in this correlation.
In physics, the susceptibility (χ) of a material or substance describes its response to an applied field. Molar susceptibility (χm) is measured as m3/mol. Magnetic susceptibility is measured by the force change felt upon the application of a magnetic field gradient [20]. Today, high-end measurement systems use a superconductive magnet. An alternative is to measure the force change on a strong compact magnet upon insertion of the sample. This system, widely used today, is called the Evans balance. For liquid samples, the susceptibility can be measured from the dependence of the NMR frequency of the sample on its shape or orientation [21]. This important property requires expensive apparatus to be measured. Thus, being able to guess it by a simple mathematical formula is quite acceptable. As can be seen from Table 2 χm has a reasonable high coefficient of determination value of 0.9411. Therefore, the regression equation can be used to predict the χm data for the missing members of the series and the rest of linear alkanes which are not considered here.
For developing a QSPR model for the unbranched alkanes the authors have considered logPoct (logarithm of octanol-water partition coefficient Poct) and aqueous solubility (Sw) to represent their physiological activity. The solubility of liquids and solids in water (Sw) as well as partition coefficient of solutes in different solvents viz. partition coefficient in octanol-water (Poct) are very important molecular properties that influence the release, transport, and the extent of absorption of drugs in the body. These properties are the key determinants of the environmental fate of agrochemicals and pollutants in the environment. The hydrophobic constant (logP) is used to rationalize interactions of small ligands with various macromolecules in the fields of biochemistry, medicinal chemistry, and environmental sciences. Considerable experience in the use of log P in the study of QSPR by regression analysis clearly indicated that measured log P should be used whenever possible. Nevertheless, when the number of compounds is great and the structural variations limited, experimentally simple economics makes it desirable to measure logPs for the key structures only and to calculate the remainder.
A number of methods are also reported for estimating the aforementioned parameters (Poct and Sw) using molecular descriptors other than topological indices. However, very little work has been done for the estimation of aforementioned parameters using topological indices. This has prompted us to undertake the present investigation in that the novel TG index has been used for modeling, monitoring, and estimating Poct and Sw. In doing so n-alkanes have been chosen (Table 1) since all these parameters for this set of compounds are easily available in the literature which can be adopted [17].
A perusal of Table 1 shows that both of the properties viz. logPoct and log Sw increase with the size of the alkanes. It means that these properties are the function of size, shape, and branching of the molecules. Hence, it appears that TG index might be appropriate for modeling, monitoring, and estimating these properties. The data presented in Table 4 show that like the presently considered properties, the magnitude of TG index also increases with the size of the alkanes under present study. This means that, TG index would be quite suitable for modeling the two properties mentioned above.
To understand the performance of the TG index, the results of regression calculations can be seen in Table 2. The TG index shows very good correlation (R2 = 0.9466, 0.9693 for logPoct and logSw, respectively) with the properties mentioned. Therefore, TG index can serve as a potential parameter for predicting the physical and physiological properties of linear alkanes.
Density is another very important physical property and easily available for the small-sized members of the series. The density of the alkanes usually increases with increasing number of carbon atoms. The R2 value for the linear regression of ln(TG) versus density exceeds 0.97. Therefore, it can be concluded that the TG index is again capable of modeling this size dependent property, useful especially for nonexistent structures.
In this study parachor is also considered for regression analysis since it is a well known property leading to calculation of a very essential property of liquids; the surface tension. A well correlated equation will give us the ability to obtain the surface tensions of liquids.
Parachor is a quantity defined by the molecular weight of a liquid times the fourth root of its surface tension, divided by the difference between the density of the liquid and the density of the vapor in equilibrium with it; essentially constant over wide ranges of temperature. Parachor has been used in solving various structural problems [22, 23].
A small structural change in a molecular scale gives a big effect on the surface tension. The estimation of the surface tension by a rather simple empirical approach using the quantity parachor has been successful for a wide variety of molecular liquids. The accuracy of the parachor approach is quite good.
It has been known that the parachor obeys an additivity rule, i.e., parachor of a molecule is always the sum of the parachor value assigned to each part of the molecule or to the atoms existing in that molecule, regardless of the type of compound. Although corrections by assigning a small value for branching, ring formation, etc., are often made in the summation of atomic parachors, additivity rule of the atomic parachor means that the isomers essentially have similar values of the molecular parachor. Also, the success of the parachor additivity rule means that the anisotropic or structure-dependent part of the molecular interaction must give only minor effects on the surface tension of molecular liquids [24]. Considerable effort has been paid to explain the empirical relation. However, there seems to be no convincing explanation of the additivity rule of the parachor, which is the essential point for the success of parachor as a method of surface tension estimation.
The coefficient of determination for the regression analysis of parachor of linear alkanes versus the TG index is 0.9471, which is a satisfactorily good result (see Table 2).
Molecular polarizability is another important property related to electron movements. Many papers have investigated the effective polarizability effects on the properties of organic compound in gas phase (such as protonic acidities and basicities) [25-27]. Previous works showed that the molecular polarizability is an important factor affecting properties of organic compounds related to positive or negative charge. The regression equation and the coefficient of determination of the analysis of polarizability of linear alkanes have been given in Table 2.
In conclusion, the TG index is a very useful tool for the estimation of the considered properties for alkanes whose data are missing and sometimes difficult (expensive and time consuming) to measure within only a few percents of error. The molecular size of the unbranched alkanes increase steadily, so does the TG index. Therefore, the TG index can be considered as successful for the correlation of size dependent physical properties. The effect of branching on the success of TG index will be investigated in the following part of the paper.
3.2. Branched Alkanes
The calculated indices and the experimental values for the eight physical properties (bp, MV, MR, HV, TC, PC, ST, mp) and coefficients of determination between the eight physical properties of the alkanes under consideration can be seen in Tables 3 and 4, respectively. A representative illustration for the calculation of the TG index for branched alkanes can be seen in Figure 1.
Before starting the correlation analyses between the novel topological index and each physical property, it is instructive to examine the correlations among the properties themselves. The results of these correlation studies are given in Table 4. As can be seen from the table, it is readily apparent that most of the properties show strong internal correlation (colinearity). Melting points are exceptional, which are very weakly correlated with the other properties. In addition to melting points, surface tensions and the critical temperatures do not correlate well with the critical pressures. For the remaining properties, all the coefficients of determination are greater than 0.807, and even exceed 0.942 for the subset (bp, MV, MR, and HV). It can be anticipated that if a given set of structural parameters successfully models a given property, this parameter set should also be reasonably successful in modeling other, strongly correlated properties. The converse can also be anticipated; i.e., lack of success should be transferred to the correlated properties.
The results of the regression analysis for branched alkanes have been given in Table 5. The properties are correlated with the logarithm of the index to obtain a linear plot.
Table 3. Calculated TG indices and experimental values for the physical properties of the 70 alkanes (Units: bp, °C; MV, cm3/mol; MR, cm3/mol; HV, kJ/mol; TC, °C; PC, atm; ST, dyn/cm; mp, °C).
| Entry | Name | TG | bp | MV | MR | HV | TC | PC | ST | mp |
| 1 | n-Butane | 9 | -0.5 | - | - | - | 152.01 | 37.47 | - | -138.35 |
| 2 | n-Pentane | 40 | 36.074 | 115.205 | 25.2656 | 26.42 | 196.62 | 33.31 | 16 | -129.72 |
| 3 | 2-Methylbutane | 32 | 27.852 | 116.426 | 25.2923 | 24.59 | 187.8 | 32.9 | 15 | -159.9 |
| 4 | n-Hexane | 169 | 68.74 | 130.688 | 29.9066 | 31.55 | 234.7 | 29.92 | 18.42 | -95.35 |
| 5 | 2-Methylpentane | 110 | 60.271 | 131.933 | 29.9459 | 29.86 | 224.9 | 29.95 | 17.38 | -153.67 |
| 6 | 3-Methylpentane | 120 | 63.282 | 129.717 | 29.8016 | 30.27 | 231.2 | 30.83 | 18.12 | -118 |
| 7 | 2,3-Dimethylbutane | 100 | 57.988 | 132.744 | 29.9347 | 29.12 | 216.2 | 30.67 | 16.3 | -99.87 |
| 8 | 2,2-Dimethylbutane | 75 | 49.741 | 130.24 | 29.8104 | 29.12 | 227.1 | 30.99 | 17.37 | -128.54 |
| 9 | n-Heptane | 448 | 98.427 | 146.54 | 34.5504 | 36.55 | 267.01 | 27.01 | 20.26 | -90.61 |
| 10 | 2-Methylhexane | 304 | 90.052 | 147.656 | 34.5908 | 34.8 | 257.9 | 27.2 | 19.29 | -118.28 |
| 11 | 3-Methylhexane | 285 | 91.85 | 145.821 | 34.4597 | 35.08 | 262.4 | 28.1 | 19.79 | -119.4 |
| 12 | 3-Ethylpentane | 288 | 93.475 | 143.517 | 34.2827 | 35.22 | 267.6 | 28.6 | 20.44 | -118.6 |
| 13 | 2,2-Dimethylpentane | 150 | 79.197 | 148.695 | 34.6166 | 32.43 | 247.7 | 28.4 | 18.02 | -123.81 |
| 14 | 2,3-Dimethylpentane | 264 | 89.784 | 144.153 | 34.3237 | 34.24 | 264.6 | 29.2 | 19.96 | -119.1 |
| 15 | 2,4-Dimethylpentane | 192 | 80.5 | 148.949 | 34.6192 | 32.88 | 247.1 | 27.4 | 18.15 | -119.24 |
| 16 | 3,3-Dimethylpentane | 252 | 86.064 | 144.53 | 34.3323 | 33.02 | 263 | 30 | 19.59 | -134.46 |
| 17 | 2,2,3-Trimethylbutane | 216 | 80.882 | 145.191 | 34.3736 | 32.04 | 258.3 | 24.64 | 18.76 | -24.91 |
| 18 | n-Octane | 1156 | 125.655 | 162.592 | 39.1922 | 41.48 | 296.2 | 24.8 | 21.76 | -56.79 |
| 19 | 2-Methylheptane | 855 | 117.647 | 163.663 | 39.2316 | 39.68 | 288 | 25.6 | 20.6 | -109.04 |
| 20 | 3-Methylheptane | 896 | 118.925 | 161.832 | 39.1001 | 39.83 | 292 | 25.6 | 21.17 | -120.5 |
| 21 | 4-Methylheptane | 756 | 117.709 | 162.105 | 39.1174 | 39.67 | 290 | 25.74 | 21 | -120.95 |
| 22 | 2,2-Dimethylhexane | 703 | 106.84 | 160.072 | 38.9441 | 37.29 | 292 | 25.6 | 21.51 | - |
| 23 | 2,3-Dimethylhexane | 729 | 115.607 | 164.285 | 39.2525 | 38.79 | 279 | 26.6 | 19.6 | -121.18 |
| 24 | 2,4-Dimethylhexane | 684 | 109.429 | 160.395 | 38.9808 | 37.76 | 293 | 25.8 | 20.99 | - |
| 25 | 2,5-Dimethylhexane | 841 | 109.103 | 163.093 | 39.13 | 37.86 | 282 | 25 | 20.05 | -137.5 |
| 26 | 3,3-Dimethylhexane | 595 | 111.969 | 164.697 | 39.2596 | 37.93 | 279 | 27.2 | 19.73 | -91.2 |
| 27 | 3,4-Dimethylhexane | 676 | 117.725 | 160.879 | 39.0087 | 39.02 | 290.84 | 27.4 | 20.63 | -126.1 |
| 28 | 3-Ethylhexane | 783 | 118.534 | 158.814 | 38.8453 | 39.4 | 298 | 27.4 | 21.64 | - |
| 29 | 2,2,3-Trimethylpentane | 476 | 109.84 | 158.794 | 38.8362 | 36.91 | 295 | 28.9 | 21.52 | -114.96 |
| 30 | 2,2,4-Trimethylpentane | 329 | 99.238 | 157.026 | 38.7171 | 35.13 | 305 | 28.2 | 21.99 | -90.87 |
| 31 | 2,3,3-Trimethylpentane | 525 | 114.76 | 159.526 | 38.9249 | 37.22 | 294 | 25.5 | 20.67 | -112.27 |
| 32 | 2,3,4-Trimethylpentane | 504 | 113.467 | 165.083 | 39.2617 | 37.68 | 271.15 | 29 | 18.77 | -107.38 |
| 33 | 3-Ethyl-2-methylpentane | 532 | 115.65 | 157.292 | 38.7617 | 38.84 | 303 | 27.6 | 21.56 | -100.7 |
| 34 | 3-Ethyl-3-methylpentane | 567 | 118.259 | 158.852 | 38.8681 | 38.48 | 295 | 24.5 | 21.14 | -109.21 |
| 35 | 2,2,3,3-Tetramethylbutane | 441 | 106.47 | - | - | - | 270.8 | 22.74 | - | - |
| 36 | n-Nonane | 2400 | 150.798 | 178.713 | 43.8423 | 46.49 | 322 | 23.6 | 22.92 | -53.52 |
| 37 | 2-Methyloctane | 2160 | 114.76 | 157.292 | 38.7617 | 37.22 | 303 | 29 | 21.56 | -100.7 |
| 38 | 3-Methyloctane | 1976 | 113.467 | 158.852 | 38.8681 | 37.61 | 295 | 27.6 | 21.14 | -109.21 |
| 39 | 4-Methyloctane | 1900 | 142.48 | 178.15 | 43.7687 | 45.09 | 318.3 | 23.98 | 22.34 | -113.2 |
| 40 | 3-Ethylheptane | 1664 | 143 | 176.41 | 43.642 | 44.96 | 318 | 23.98 | 22.81 | -114.9 |
| 41 | 4-Ethylheptane | 1572 | 141.2 | 175.685 | 43.4907 | 45 | 318.3 | 22.8 | 22.81 | - |
| 42 | 2,2-Dimethylheptane | 1408 | 132.69 | 180.507 | 43.9138 | 41.82 | 302 | 23.79 | 20.8 | -113 |
Table 3. (Continued)
| 43 | 2,3-Dimethylheptane | 1600 | 140.5 | 176.653 | 43.6269 | 43.51 | 315 | 22.7 | 22.34 | -116 |
| 44 | 2,4-Dimethylheptane | 1323 | 133.5 | 179.12 | 43.7393 | 43.31 | 306 | 22.7 | 21.3 | - |
| 45 | 2,5-Dimethylheptane | 1683 | 136 | 179.371 | 43.8484 | 42.91 | 307.8 | 23.7 | 21.3 | - |
| 46 | 2,6-Dimethylheptane | 1496 | 135.21 | 180.914 | 43.9258 | 42.3 | 306 | 24.19 | 20.83 | -102.9 |
| 47 | 3,3-Dimethylheptane | 1512 | 137.3 | 176.897 | 43.687 | 42.78 | 314 | 24.77 | 22.01 | - |
| 48 | 3,4-Dimethylheptane | 1457 | 140.6 | 175.349 | 43.5473 | 43.44 | 322.7 | 23.59 | 22.8 | - |
| 49 | 3,5-Dimethylheptane | 1586 | 136 | 177.386 | 43.6378 | 43.49 | 312.3 | 24.18 | 21.77 | - |
| 50 | 4,4-Dimethylheptane | 1140 | 135.2 | 176.897 | 43.6022 | 43.09 | 317.8 | 24.77 | 22.01 | - |
| 51 | 3-Ethyl-2-methylhexane | 1395 | 138 | 175.445 | 43.655 | 43.65 | 322.7 | 25.56 | 22.8 | - |
| 52 | 4-Ethyl-2-methylhexane | 1496 | 133.8 | 177.386 | 43.6472 | 43.26 | 330.3 | 25.66 | 21.77 | - |
| 53 | 3-Methyl-3-ethylhexane | 1280 | 140.6 | 173.077 | 43.268 | 43.11 | 327.2 | 23.59 | 23.22 | - |
| 54 | 3-Ethyl-4-methylhexane | 1320 | 140.4 | 172.844 | 43.3746 | 43.79 | 312.3 | 25.07 | 23.27 | - |
| 55 | 2,2,3-Trimethylhexane | 1271 | 133.6 | 175.878 | 43.6226 | 41.5 | 318.1 | 23.39 | 21.86 | - |
| 56 | 2,2,4-Trimethylhexane | 1155 | 126.54 | 179.22 | 43.7638 | 40.83 | 301 | 22.41 | 20.51 | -120 |
| 57 | 2,2,5-Trimethylhexane | 1496 | 124.084 | 181.346 | 43.9356 | 40.03 | 296.6 | 25.56 | 20.04 | -105.78 |
| 58 | 2,3,3-Trimethylhexane | 1120 | 137.68 | 173.78 | 43.4347 | 41.91 | 326.1 | 25.46 | 22.41 | -116.8 |
| 59 | 2,3,4-Tri methylhexane | 1260 | 139 | 173.498 | 43.3917 | 42.45 | 324.2 | 23.49 | 22.8 | - |
| 60 | 2,3,5-Trimethylhexane | 1408 | 131.34 | 177.656 | 43.6474 | 41.8 | 309.4 | 23.79 | 21.27 | -127.8 |
| 61 | 2,4,4-Trimethylhexane | 1080 | 130.648 | 177.187 | 43.6598 | 41.25 | 309.1 | 26.45 | 21.17 | -113.38 |
| 62 | 3,3,4-Trimethylhexane | 1131 | 140.46 | 172.055 | 43.3407 | 41.99 | 330.6 | 26.94 | 23.27 | -101.2 |
| 63 | 3,3-Diethylpentane | 1584 | 146.168 | 170.185 | 43.1134 | 43.1 | 342.8 | 25.96 | 23.75 | -33.11 |
| 64 | 2,2-Dimethyl-3-ethylpentane | 864 | 133.83 | 174.537 | 43.4571 | 41.63 | 322.6 | 26.94 | 22.38 | -99.2 |
| 65 | 2,3-Dimethyl-3-ethylpentane | 1008 | 142 | 170.093 | 42.9542 | 42.01 | 338.6 | 25.46 | 23.87 | - |
| 66 | 2,4-Dimethyl-3-ethylpentane | 896 | 136.73 | 173.804 | 43.4037 | 42.38 | 324.2 | 27.04 | 22.8 | -122.2 |
| 67 | 2,2,3,3-Tetramethylpentane | 988 | 140.274 | 169.495 | 43.2147 | 40.07 | 334.5 | 25.66 | 23.38 | -9.9 |
| 68 | 2,2,3,4-Tetramethylpentane | 832 | 133.016 | 173.557 | 43.4359 | 40.25 | 319.6 | 24.58 | 21.98 | -121.09 |
| 69 | 2,2,4,4-Tetramethylpentane | 528 | 122.284 | 178.256 | 43.8747 | 38.41 | 301.6 | 26.85 | 20.37 | -66.54 |
| 70 | 2,3,3,4-Tetramethylpentane | 960 | 141.551 | 169.928 | 43.2016 | 40.81 | 334.5 | 29.75 | 23.31 | -102.12 |
According to the results of the regression analyses, the novel TG index is successful for modeling most of the properties considered. In the previous section, the success of the index had been proved over the linear alkane series. The results obtained in this part of the article indicate that the novel TG index is also capable of reflecting the effect of branching in molecules. Small variations in between the values of the coefficients of determination are not due to the failure of the index but the improper correlations between the properties themselves. The index correlated best with boiling point (R2 = 0.9595) and heat of vaporization (R2 = 0.9639).
The failure of the present index to model the melting points of the presently considered 70 alkane molecules is not surprising; a similar result was obtained by Seybold et al. [28]. A melting transition maintains a condensed phase and involves a partial disruption of intermolecular orientations. Therefore, melting might depend on some geometrical and other crystalline factors, which are not well defined with any topological descriptors, yet.
3.3. Cycloalkanes
Cycloalkanes (also called naphthenes, especially if from petroleum sources) are types of alkanes which have one or more rings of carbon atoms in the chemical structure of their molecules. Cycloalkanes consist of only carbon (C) and hydrogen (H) atoms and are saturated because there are no multiple C-C bonds to hydrogenate. A general chemical formula for cycloalkanes would be CnH2(n+1-g) where n = number of C atoms and g = number of rings in the molecule. Cycloalkanes with a single ring are named analogously to their normal alkane counterpart of the same carbon count: cyclopropane, cyclobutane, cyclopentane, cyclohexane, etc. The larger cycloalkanes, with greater than 20 carbon atoms are typically called cycloparaffins.
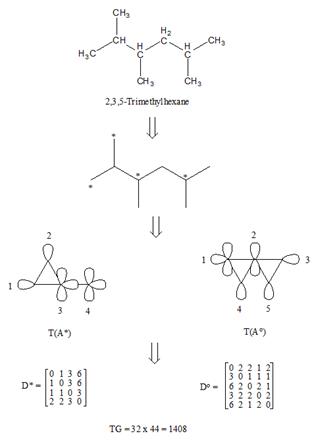
Figure 1. Calculation of the TG index for 2,3,5-trimethyl hexane (Entry 60).
Table 4. Coefficients of determination (R2) among the properties examined, for branched alkanes considered presently.
| bp | MV | MR | HV | TC | PC | ST | mp | |
| bp | 1.000 | |||||||
| MV | 0.956 | 1.000 | ||||||
| MR | 0.975 | 0.992 | 1.000 | |||||
| HV | 0.981 | 0.946 | 0.952 | 1.000 | ||||
| TC | 0.975 | 0.909 | 0.951 | 0.930 | 1.000 | |||
| PC | -0.838 | -0.841 | -0.823 | -0.842 | -0.778 | 1.000 | ||
| ST | 0.923 | 0.807 | 0.865 | 0.892 | 0.965 | -0.688 | 1.000 | |
| mp | 0.397 | 0.293 | 0.329 | 0.319 | 0.432 | -0.354 | 0.421 | 1.000 |
Table 5. The regression equation and the coefficient of determination between the natural logarithm of the TG index and branched alkanes.
| Property | regression equation | R2 |
| bp (n = 70) | y = 28.446x - 68.686 | 0.9595 |
| MV (n = 68) | y = 16.385x + 56.678 | 0.9116 |
| MR (n = 68) | y = 4.9354x + 7.593 | 0.9125 |
| HV (n = 68) | y = 4.6939x + 6.7157 | 0.9639 |
| TC (n = 70) | y = 32.959x + 78.730 | 0.8772 |
| PC (n = 70) | y = -2.3142x + 41.249 | 0.7718 |
| ST (n = 68) | y = 1.7268x + 9.7065 | 0.7541 |
| mp (n = 52) | y = 9.0646x - 163.16 | 0.1348 |
Cycloalkanes are classified into small, common, medium, and large cycloalkanes, where cyclopropane and cyclobutane are the small ones, cyclopentane, cyclohexane, cycloheptane are the common ones, cyclooctane through cyclotridecane are the medium ones, and the rest are the larger ones. Cycloalkanes are similar to alkanes in their general physical properties, but they have higher boiling points, melting points, and densities than alkanes.
Table 6. The TG index and experimental boiling points (°C) of cyclohexane systems with 6-10 carbon atoms.
| Name | TG | bp | |
| 1 | c6 | 144 | 80.7 |
| 2 | 1mc6 | 336 | 101 |
| 3 | 1ec6 | 840 | 131.8 |
| 4 | 14mc6 | 784 | 121.8 |
| 5 | 13mc6 | 640 | 122.3 |
| 6 | 12mc6 | 729 | 126.6 |
| 7 | 11mc6 | 640 | 119.5 |
| 8 | 1pc6 | 1820 | 156.7 |
| 9 | 1ipc6 | 1536 | 154.8 |
| 10 | 1m4ec6 | 1700 | 150.8 |
| 11 | 1m3ec6 | 1564 | 150 |
| 12 | 1m2ec6 | 1457 | 154.3 |
| 13 | 135mc6 | 1080 | 139.5 |
| 14 | 124mc6 | 1395 | 144.8 |
| 15 | 123mc6 | 1320 | 149.4 |
| 16 | 1m1ec6 | 1485 | 152 |
| 17 | 113mc6 | 1062 | 136.6 |
| 18 | 112mc6 | 1350 | 145.1 |
| 19 | 1bc6 | 3840 | 180.9 |
| 20 | 1ibc6 | 3078 | 171.3 |
| 21 | 1m4pc6 | 3481 | 173.4 |
| 22 | 1m3pc6 | 2964 | 169 |
| 23 | 1sbc6 | 3078 | 179.3 |
| 24 | 14ec6 | 3249 | 175.5 |
| 25 | 13ec6 | 3016 | 172 |
| 26 | 1m2pc6 | 3078 | 174.5 |
| 27 | 1m4ipc6 | 2664 | 170 |
| 28 | 12ec6 | 2809 | 176 |
| 29 | 1m3ipc6 | 2808 | 167 |
| 30 | 1e35mc6 | 2584 | 168.5 |
| 31 | 1m2ipc6 | 2415 | 171 |
| 32 | 1m1pc6 | 2774 | 174.3 |
| 33 | 1tbc6 | 2268 | 171.5 |
| 34 | 11ec6 | 2592 | 179.5 |
| 35 | 14m1ec6 | 2695 | 168 |
| 36 | 1245mc6 | 2500 | 167 |
| 37 | 13m1ec6 | 2516 | 166.6 |
| 38 | 1235mc6 | 2244 | 166.5 |
| 39 | 1234mc6 | 2401 | 172.5 |
| 40 | 1135mc6 | 1640 | 153 |
Although, boiling points of alkanes are traditionally used for testing and/or demonstrating the correlating abilities of topological indices. Boiling points of cycloalkanes have been examined to a much lesser extent [29,30]. Moreover, Rücker and Rücker [31] produced a critical compilation of experimental boiling points of cycloalkanes and reported their correlations with numerous topological indices and (linear) combinations. In this part of the text, novel QSPR models have been extended over the boiling points of cycloalkanes.
The calculated TG indices and the experimental boiling point data of the cyclohexanes with 6-10 carbon atoms, and the plot of bp (°C) versus ln(TG) have been given in Table 6 and Figure 2, respectively. As in the case of linear and branched alkanes, the TG index and the boiling point increases with the number of carbon atoms present in the structure. The regression analysis yielded 0.9721 for the coefficient of determination. Consequently, the TG index has proved itself as a successful parameter for modeling the cyclic systems as well.
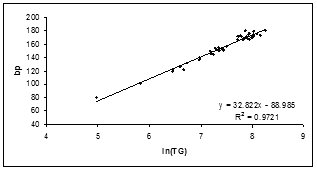
Figure 2. The plot of boiling points of cyclohexane derivatives versus ln(TG)
3.4. Alkenes
In the previous part, the topological descriptors have been applied to some physical and electronic properties of a set of normal and branched alkanes. In that part, it has been found that the TG index is successful in obtaining high-quality structure-property relationships. Good regression equations were obtained for most of the physical properties of the alkanes (the melting points (mp), traditionally a subtle and difficult property to handle, were an exception). In this part of the work, the TG index has been employed as a structural measure for the physical and chemical properties of a set of monoalkenes, where a new structural feature, the double bond, is introduced. Only a few previous QSPR studies have been devoted to the properties of this class of compounds [32-35], and these have generally been limited to single properties.
The properties examined in this point of the study are: boiling points (bp), molar refractions (MR), molar volumes (MV) at 20°C, heats of combustion (HC), molar heats of vaporization (HV) at 25°C, flashpoints (FLASH), second virial coefficients (VIRC) at 25°C, critical temperatures (TC), critical pressures (PC), and melting points (mp). The property values were excerpted from the reference source [36]. MV values were calculated as MW/d, where MW is the molecular weight, and d is the density (g/cm3) at 20°C.
The calculated indices, and the experimental values for the eleven properties, of the alkenes under consideration can be seen in Tables 7 and Table 8, respectively.
Table 7. The TG indices and the experimental values for the physical properties of the alkenes series considered (Units: bp, °C; mp, °C; MV, cm3/mol; MR, cm3/mol; HC, kJ/mol; FLASH, K; VIRC, cm3/mol; HV, kJ/mol; TC, °C; PC, MPa).
| Name | TG | bp | mp | MR | MV | HC | HV | FLASH | VIRC | TC | PC |
| 1-Butene | 16 | -6.3 | -185.4 | 22.66 | 94.3 | 2716.8 | 20204 | - | -650 | 146.5 | 4.02 |
| Cis-2-butene | 16 | 3.7 | -138.9 | 20.59 | 90.3 | 2710.0 | 21963 | - | -713 | 162.4 | 4.21 |
| Trans-2-butene | 16 | 0.9 | -105.6 | 20.73 | 21483 | - | -700 | 155.5 | 4.10 | ||
| 1-Pentene | 65 | 30.0 | -165.2 | 24.85 | 109.4 | 3375.4 | 25501 | - | -1093 | 191.6 | 3.53 |
| Cis-2-pentene | 60 | 36.9 | -151.4 | 24.95 | 107.0 | 3370.0 | 26885 | - | -1150 | 201.8 | 3.70 |
| Trans-2-pentene | 60 | 37.0 | -140.2 | 25.02 | - | - | - | 228.15 | -1140 | 201.9 | 3.65 |
| 2-Methyl-1-butene | 45 | 31.2 | -137.6 | 24.85 | 107.8 | 3361.6 | - | - | -1111 | 191.9 | 3.51 |
| 3-Methyl-1-butene | 50 | 20.1 | -168.5 | 24.94 | 111.8 | 3368.9 | - | - | -974 | 191.9 | 3.44 |
| 2-Methyl-2-butene | 50 | 38.6 | -133.8 | 24.95 | 105.9 | 3355.7 | 27090 | 228.15 | -1264 | 197.2 | 3.38 |
| 1-Hexene | 256 | 63.5 | -139.8 | 29.49 | 125.0 | 4034.1 | 30587 | 247.15 | -1729 | 230.8 | 3.14 |
| Cis-2-hexene | 240 | 68.8 | -141.1 | 29.53 | 122.5 | 4023.8 | 33744 | - | - | - | - |
| Trans-2-hexene | 240 | 67.9 | -133.0 | 29.67 | - | 32136 | 253.15 | - | - | - | |
| Cis-3-hexene | 225 | 66.4 | -137.8 | 29.66 | 123.8 | 4028.5 | 31724 | - | - | - | - |
| Trans-3-hexene | 225 | 67.1 | -113.4 | 29.75 | - | 32072 | 261.15 | - | - | - | |
| 2-Methyl-1-pentene | 138 | 60.7 | -135.7 | 29.48 | 123.8 | 4016.8 | 31042 | 247.15 | - | - | - |
| 3-Methyl-1-pentene | 180 | 54.1 | -153.0 | 29.49 | 126.1 | 4026.1 | 29262 | 245.15 | - | - | - |
| 4-Methyl-1-pentene | 144 | 53.9 | -153.6 | 29.55 | 126.8 | 4024.9 | 29376 | 242.15 | - | - | - |
| 2-Methyl-2-pentene | 132 | 67.3 | -135.1 | 29.74 | 122.6 | 4007.3 | 32088 | 250.15 | - | - | - |
| 3-Methyl-cis-2-pentene | 168 | 70.5 | -138.4 | 29.55 | 122.2 | 4013.9 | 31812 | - | - | - | - |
| 3-Methyl-trans-2-pentene | 168 | 67.6 | -134.8 | 29.55 | - | - | 32536 | - | - | - | - |
| 4-Methyl-cis-2-pentene | 132 | 56.3 | -134.4 | 29.67 | 125.8 | 4018.7 | 30096 | 245.15 | - | - | - |
| 4-Methyl-trans-2-pentene | 132 | 58.6 | -140.8 | 29.75 | - | - | 30550 | - | - | - | - |
| 2-Ethyl-1-butene | 168 | 64.7 | -131.5 | 29.37 | 122.0 | 4020.2 | 31614 | - | - | - | - |
| 2,3-Dimethyl-1-butene | 144 | 55.7 | -157.3 | 29.43 | 124.1 | 4011.2 | 29800 | 255.15 | - | - | - |
| 3,3-Dimethyl-1-butene | 108 | 41.2 | -115.2 | 29.58 | 128.9 | 4015.4 | 27449 | 245.15 | - | - | - |
| 2,3-Dimethyl-2-butene | 144 | 73.2 | -74.3 | 29.59 | 118.8 | 4007.3 | 32476 | 257.15 | -1929 | - | - |
| 1-Heptene | 646 | 93.6 | -119.0 | 34.13 | 140.9 | 4692.6 | 35484 | 272.15 | -2810 | 264.1 | - |
| Cis-2-heptene | 608 | 98.5 | - | 34.17 | 138.9 | 4686.5 | - | - | - | - | - |
| Trans-2-heptene | 608 | 98.0 | -109.5 | 34.28 | - | - | - | 272.15 | - | - | - |
| Cis-3-heptene | 576 | 95.8 | - | 34.31 | 139.7 | 4686.5 | - | - | - | - | - |
| Trans-3-heptene | 576 | 95.7 | -136.6 | 34.43 | - | - | - | - | - | - | - |
| 2-Methyl-1-hexene | 532 | 92.0 | -102.8 | 34.12 | 139.7 | 4678.0 | - | 267.15 | - | - | - |
| 3-Methyl-1-hexene | 486 | 84.0 | - | 34.16 | 142.0 | 4688.7 | - | 267.15 | - | - | - |
| 4-Methyl-1-hexene | 504 | 86.7 | -141.5 | 34.08 | 140.6 | 4688.7 | - | - | - | - | - |
| 5-Methyl-1-hexene | 551 | 85.3 | - | 34.14 | 141.9 | 4686.0 | - | - | - | - | - |
| 2-Methyl-2-hexene | 513 | 95.4 | -130.4 | 34.40 | 138.7 | 4672.2 | - | - | - | - | - |
| 3-Methyl-cis-2-hexene | 459 | 94.0 | - | 34.18 | 137.2 | 4674.9 | - | - | - | - | - |
| 3-Methyl-trans-2-hexene | 459 | 94.0 | - | 34.19 | 137.5 | 4674.9 | - | - | - | - | - |
| 4-Methyl-cis-2-hexene | 468 | 87.4 | - | 34.22 | - | - | - | - | - | - | - |
| 4-Methyl-trans-2-hexene | 468 | 87.6 | -126.5 | 34.35 | - | - | - | - | - | - | - |
| 5-Methyl-cis-2-hexene | 522 | 91.0 | - | 34.20 | 139.9 | 4679.3 | - | - | - | - | - |
| 5-Methyl-trans-2-hexene | 522 | 86.0 | - | 34.41 | - | - | - | - | - | - | - |
Table 7. (Continued)
| 2-Methyl-cis-3-hexene | 486 | 86.0 | - | 34.37 | 141.5 | 4679.3 | - | - | - | ||||||
| 2-Methyl-trans-3-hexene | 486 | 86.0 | - | 34.52 | - | - | - | - | - | ||||||
| 3-Methyl-cis-3-hexene | 494 | 95.4 | - | 34.32 | 137.7 | 4674.9 | - | - | - | ||||||
| 3-Methyl-trans-3-hexene | 494 | 93.6 | - | 34.34 | - | - | - | - | - | ||||||
| 2-Ethyl-1-pentene | 459 | 94.0 | 33.99 | 138.7 | 4680.7 | - | - | - | - | - | |||||
| 3-Ethyl-1-pentene | 406 | 85.1 | -127.4 | 34.06 | 141.1 | 4691.3 | - | - | - | - | - | ||||
| 2,3-Dimethyl-1-pentene | 364 | 84.3 | -134.8 | 34.00 | 139.2 | 4673.8 | - | - | - | - | - | ||||
| 2,4-Dimethyl-1-pentene | 266 | 81.6 | -123.8 | 34.18 | 141.5 | 4670.9 | 33344 | - | - | - | - | ||||
| 3,3-Dimethyl-1-pentene | 357 | 77.5 | -134.3 | 34.01 | 140.8 | 4679.4 | - | - | - | - | - | ||||
| 3,4-Dimethyl-1-pentene | 378 | 81.0 | - | 34.05 | 140.7 | 4681.7 | - | - | - | - | - | ||||
| 4,4-Dimethyl-1-pentene | 259 | 72.5 | -136.6 | 34.23 | 143.9 | 4674.7 | 31598 | - | - | - | - | ||||
| 3-Ethyl-2-pentene | 442 | 96.0 | - | 34.11 | 136.3 | 4677.5 | - | - | - | - | - | ||||
| 2,3-Dimethyl-2-pentene | 350 | 97.5 | -118.3 | 34.22 | 134.9 | 4667.1 | - | - | - | - | - | ||||
| 2,4-Dimethyl-2-pentene | 252 | 83.4 | - | 34.53 | 141.3 | 4665.1 | 34418 | - | - | - | - | ||||
| 3,4-Dimethyl-cis-2-pentene | 350 | 87.0 | - | 34.12 | 137.6 | 4667.9 | - | - | - | - | - | ||||
| 3,4-Dimethyl-trans-2-pentene | 350 | 87.0 | - | 34.15 | - | - | - | - | - | - | - | ||||
| 4,4-Dimethyl-cis-2-pentene | 238 | 80.4 | -135.5 | 34.23 | 140.4 | 4667.9 | 32973 | - | - | - | - | ||||
| 4, 4-Dimethyl-trans-2-pentene | 238 | 76.8 | -115.2 | 34.41 | - | - | 33187 | - | - | - | - | ||||
| 2-Ethyl-3-methyl-1-butene | 350 | 89.0 | - | 33.96 | 138.5 | 4673.7 | 34634 | - | - | - | - | ||||
| 2,3,3-Trimethyl-1-butene | 322 | 77.9 | -119.9 | 33.99 | 139.3 | 4668.2 | 32485 | 256.15 | - | - | |||||
| 1-Octene | 1600 | 121.3 | -101.7 | 38.78 | 157.0 | 5351.1 | 41224 | - | -3948 | - | - | ||||
| Cis-2-octene | 1520 | 125.6 | -100.2 | 38.79 | 154.9 | - | - | - | - | - | - | ||||
| Trans-2-octene | 1520 | 125.0 | -87.7 | 38.88 | - | ||||||||||
| Cis-3-octene | 1444 | 122.9 | - | 38.85 | 155.8 | ||||||||||
| Trans-3-octene | 1444 | 123.3 | - | 39.09 | |||||||||||
| Cis-4-octene | 1444 | 122.5 | - | 38.94 | 155.6 | - | - | - | - | - | - | ||||
| Trans-4-octene | 1444 | 122.3 | - | 39.08 | - | - | - | - | - | - | |||||
| 2-Methyl-1-heptene | 1144 | 119.3 | - | 38.78 | 155.7 | - | - | - | - | - | - | ||||
| 3-Methyl-1-heptene | 1216 | 111.0 | - | 38.76 | 157.8 | - | - | - | - | - | - | ||||
| 4-Methyl-1-heptene | 1050 | 112.8 | - | 38.77 | 156.5 | - | - | - | - | - | - | ||||
| 5-Methyl-1-heptene | 1254 | 113.3 | - | 38.76 | 156.6 | - | - | - | - | - | - | ||||
| 6-Methyl-1-heptene | 1188 | 113.2 | - | 38.79 | 157.6 | - | - | - | - | - | - | ||||
| 2-Methyl-2-heptene | 1100 | 122.6 | - | 38.97 | 155.0 | - | - | - | - | - | - | ||||
| 3-Methyl-cis-2-heptene | 1152 | 122.0 | - | 38.87 | 153.9 | - | - | - | - | - | - | ||||
| 3-Methyl-trans-2-heptene | 1152 | 122.0 | - | 38.87 | - | - | - | - | - | - | |||||
| 4-Methyl-cis-2-heptene | 987 | 114.0 | - | 38.83 | 156.7 | - | - | - | - | - | - | ||||
| 4-Methyl-trans-2-heptene | 987 | 114.0 | - | 38.83 | - | - | - | - | - | - | |||||
| 5-Methyl-cis-2-heptene | 1188 | 118.0 | - | 38.78 | 155.2 | - | - | - | - | - | - | ||||
| 5-Methyl-trans-2-heptene | 1188 | 118.0 | - | 38.78 | - | - | - | - | - | - | |||||
| 6-Methyl-cis-2-heptene | 1122 | 117.0 | - | 38.89 | 156.3 | - | - | - | - | - | - | ||||
| 6-Methyl-trans-2-heptene | 1122 | 117.0 | - | 38.89 | - | - | - | - | - | - | |||||
| 2-Methyl-cis-3-heptene | 1050 | 112.0 | - | 39.12 | 158.9 | - | - | - | - | - | - | ||||
| 2-Methyl-trans-3-heptene | 1050 | 112.0 | - | 39.12 | - | - | - | - | - | - | |||||
| 3-Methyl-cis-3-heptene | 1116 | 121.0 | - | 38.84 | 154.1 | - | - | - | - | - | - | ||||
Table 7. (Continued)
| 3-Methyl-trans-3-heptene | 1116 | 121.0 | - | 38.84 | - | - | - | - | - | - | |
| 4-Methyl-cis-3-heptene | 980 | 122.0 | - | 38.92 | 154.8 | - | - | - | - | - | - |
| 4-Methyl-trans-3-heptene | 980 | 122.0 | - | 38.92 | - | - | - | - | - | - | |
| 5-Methyl-cis-3-heptene | 1116 | 112.0 | - | 38.99 | 157.4 | - | - | - | - | - | - |
| 5-Methyl-trans-3-heptene | 1116 | 112.0 | - | 38.99 | - | - | - | - | - | - | |
| 6-Methyl-cis-3-heptene | 1071 | 115.0 | - | 38.99 | 157.4 | - | - | - | - | - | - |
| 6-Methyl-trans-3-heptene | 1071 | 115.0 | - | 38.99 | - | - | - | - | - | - | |
| 2-Ethyl-1-hexene | 1152 | 120.0 | - | 38.71 | 154.3 | - | - | - | - | - | - |
| 3-Ethyl-1-hexene | 1054 | 110.3 | - | 38.63 | 156.9 | - | - | - | - | - | - |
| 4-Ethyl-1-hexene | 1088 | 113.0 | - | 38.46 | 154.6 | - | - | - | - | - | - |
| 2,3-Dimethyl-1-hexene | 961 | 110.5 | - | 38.70 | 155.5 | - | - | - | - | - | - |
| 2,4-Dimethyl-1-hexene | 924 | 111.2 | - | 38.70 | 155.8 | - | - | - | - | - | - |
| 2,5-Dimethyl-1-hexene | 1122 | 111.6 | - | 38.80 | 156.5 | - | - | - | - | - | - |
| 3,3-Dimethyl-1-hexene | 800 | 104.0 | - | 38.69 | 157.2 | - | - | - | - | - | - |
| 3,4-Dimethyl-1-hexene | 930 | 112.0 | - | 38.65 | 155.0 | - | - | - | - | - | - |
| 3,5-Dimethyl-1-hexene | 924 | 104.0 | - | 38.76 | 158.5 | - | - | - | - | - | - |
| 4,4-Dimethyl-1-hexene | 840 | 107.2 | - | 38.64 | 155.9 | - | - | - | - | - | - |
| 4,5-Dimethyl-1-hexene | 1024 | 109.0 | - | 38.52 | 154.1 | - | - | - | - | - | - |
| 5,5-Dimethyl-1-hexene | 968 | 102.5 | - | 38.78 | 158.3 | - | - | - | - | - | - |
| 3-Ethyl-cis-2-hexene | 992 | 121.0 | - | 38.85 | 152.3 | - | - | - | - | - | - |
| 3-Ethyl-trans-2-hexene | 992 | 121.0 | - | 38.85 | - | - | - | - | - | - | |
| 4-Ethyl-cis-2-hexene | 1020 | 113.0 | - | 38.51 | 154.8 | - | - | - | - | - | - |
| 4-Ethyl-trans-2-hexene | 1020 | 113.0 | - | 38.51 | - | - | - | - | - | - | |
| 2,3-Dimethyl-2-hexene | 837 | 121.8 | -115.1 | 38.87 | 151.5 | - | - | - | - | - | - |
| 2,4-Dimethyl-2-hexene | 882 | 110.6 | - | 38.69 | 155.6 | - | - | - | - | - | - |
| 2,5-Dimethyl-2-hexene | 1054 | 112.2 | - | 38.94 | 155.8 | - | - | - | - | - | - |
| 3,4-Dimethyl-cis-2-hexene | 870 | 116.0 | - | 38.37 | 152.3 | - | - | - | - | - | - |
| 3,4-Dimethyl-trans-2-hexene | 870 | 116.0 | - | 38.37 | - | - | - | - | - | - | |
| 3,5-Dimethyl-cis-2-hexene | 880 | 112.0 | - | 38.84 | 154.8 | - | - | - | - | - | - |
| 3,5-Dimethyl-trans-2-hexene | 880 | 112.0 | - | 38.84 | - | - | - | - | - | - | |
| 4,4-Dimethyl-cis-2-hexene | 780 | 106.0 | - | 38.75 | 155.4 | - | - | - | - | - | - |
| 4,4-Dimethyl-trans-2-hexene | 780 | 106.0 | - | 38.75 | - | - | - | - | - | - | |
| 4,5-Dimethyl-cis-2-hexene | 960 | 110.0 | - | 38.59 | 154.8 | - | - | - | - | - | - |
| 4,5-Dimethyl-trans-2-hexene | 960 | 110.0 | - | 38.59 | - | - | - | - | - | - | |
| 5,5-Dimethyl-cis-2-hexene | 924 | 106.9 | - | 38.89 | 156.5 | - | - | - | - | - | - |
| 5,5-Dimethyl-trans-2-hexene | 924 | 104.1 | - | 38.96 | - | - | - | - | - | - | |
| 3-Ethy1-3-hexene | 870 | 116.0 | 38.79 | 153.9 | - | - | - | - | - | - | |
| 2,2-Dimethyl-cis-3-hexene | 861 | 105.4 | -137.4 | 38.99 | 157.4 | - | - | - | - | - | - |
| 2,2-Dimethyl-trans-3-hexene | 861 | 100.9 | - | 39.18 | - | - | - | - | - | - | |
| 2,3-Dimethyl-cis-3-hexene | 900 | 114.0 | - | 38.68 | 154.1 | - | - | - | - | - | - |
| 2,3-Dimethyl-trans-3-hexene | 900 | 114.0 | - | 38.68 | - | - | - | - | - | - | |
| 2,4-Dimethyl-cis-3-hexene | 840 | 109.0 | - | 39.06 | 156.3 | - | - | - | - | - | - |
| 2,4-Dimethyl-trans-3-hexene | 840 | 107.6 | - | 39.13 | - | - | - | - | - | - | |
| 2,5-Dimethyl-cis-3-hexene | 1024 | 102.0 | - | 38.82 | 158.0 | - | - | - | - | - | - |
Table 7. (Continued)
| 2,5-Dimethyl-trans-3-hexene | 1024 | 102.0 | - | 38.82 | - | - | - | - | - | - | |||||
| 3,4-Dimethyl-cis-3-hexene | 841 | 122.0 | - | 38.80 | 150.2 | - | - | - | - | - | - | ||||
| 3,4-Dimethyl-trans-3-hexene | 841 | 122.0 | - | 38.80 | - | - | - | - | - | - | |||||
| 2-n-Propyl-1-pentene | 960 | 117.7 | - | 38.70 | 155.0 | - | - | - | - | - | - | ||||
| 2-Isopropyl-1-pentene | 930 | 113.0 | - | 38.67 | 154.8 | - | - | - | - | - | - | ||||
| 2-Ethyl-3-methyl-1-pentene | 870 | 112.5 | - | 38.48 | 15.9 | - | - | - | - | - | - | ||||
| 2-Ethyl-4-methyl-1-pentene | 880 | 110.3 | - | 38.68 | 156.0 | - | - | - | - | - | - | ||||
| 3-Ethyl-2-methyl-1-pentene | 856 | 110.0 | - | 38.49 | 153.7 | - | - | - | - | - | - | ||||
| 3-Ethyl-3-methyl-1-pentene | 768 | 112.0 | - | 38.71 | 153.6 | - | - | - | - | - | - | ||||
| 3-Ethyl-4-methyl-1-pentene | 720 | 107.5 | - | 38.59 | 155.8 | - | - | - | - | - | - | ||||
| 2,3,3-Trimethyl-1-pentene | 696 | 108.3 | -69.0 | 38.41 | 152.6 | - | - | - | - | - | - | ||||
| 2,3,4-trimethyl-1-pentene | 672 | 108.0 | - | 38.54 | 153.9 | - | - | - | - | - | - | ||||
| 2,4,4-Trimethyl-1-pentene | 440 | 101.4 | -93.5 | 38.77 | 156.9 | - | - | - | - | - | - | ||||
| 3,3,4-Trimethyl-1-pentene | 720 | 105.0 | - | 38.50 | 153.9 | - | - | - | - | - | - | ||||
| 3,4,4-Trimethyl-1-pentene | 560 | 104.0 | - | 38.83 | 156.1 | - | - | - | - | - | - | ||||
| 3-Ethyl-2-methyl-2-pentene | 672 | 117.0 | - | 38.80 | 151.8 | - | - | - | - | - | - | ||||
| 3-Ethyl-4-methyl-cis-2-pentene | 672 | 116.0 | - | 38.74 | 151.8 | - | - | - | - | - | - | ||||
| 3-Ethyl-4-methyl-trans-2-pentene | 672 | 114.3 | - | 38.71 | - | - | - | - | - | - | |||||
| 2,3,4-Trimethyl-2-pentene | 640 | 116.3 | -133.3 | 38.79 | 150.9 | - | - | - | - | - | - | ||||
| 2,4,4-Trimethyl-2-pentene | 364 | 104.9 | -106.3 | 39.01 | 155.5 | - | 37224 | - | - | - | - | ||||
| 3,4,4-Trimethyl-cis-2-pentene | 608 | 112.0 | - | 38.66 | 151.8 | - | - | - | - | - | - | ||||
| 3,4,4-Trimethyl-trans-2-pentene | 608 | 112.0 | - | 38.66 | - | - | - | - | - | - | |||||
| 2-Isopropyl-3-methyl-1-butene | 640 | 104.0 | - | 38.38 | 155.4 | - | - | - | - | - | - | ||||
| 2-Ethyl-3,3-dimethyl-1-butene | 608 | 110.0 | - | 38.67 | 154.1 | - | - | - | - | - | - | ||||
| 1-Nonene | 3220 | 146.9 | -81.4 | 43.45 | 173.2 | 6010.1 | - | - | - | 320.1 | 2.33 | ||||
| Cis-2-nonene | 3082 | 150.8 | - | - | - | - | - | - | - | - | - | ||||
| Trans-2-nonene | 3082 | 150.1 | - | - | - | - | - | - | - | - | - | ||||
| Cis-3-nonene | 2992 | 148.4 | - | - | - | - | - | - | - | - | - | ||||
| Trans-3-nonene | 2992 | 148.2 | - | - | - | - | - | - | - | - | - | ||||
| Cis-4-nonene | 2904 | 147.4 | - | - | - | - | - | - | - | - | - | ||||
| Trans-4-nonene | 2904 | 147.8 | - | - | - | - | - | - | - | - | - | ||||
Table 8. Coefficients of determination among the properties of the alkene series examined.
| bp | MR | MV | HC | HV | FLASH | VIRC | TC | PC | mp | |
| bp | 1.000 | |||||||||
| MR | 0.967 | 1.000 | ||||||||
| MV | 0.946 | 0.992 | 1.000 | |||||||
| HC | 0.970 | 0.996 | 0.992 | 1.000 | ||||||
| HV | 0.993 | 0.921 | 0.903 | 0.938 | 1.000 | |||||
| FLASH | 0.933 | 0.905 | 0.844 | 0.897 | 0.878 | 1.000 | ||||
| VIRC | -0.960 | -0.981 | -0.969 | -0.976 | -0.974 | -0.975 | 1.000 | |||
| TC | 0.996 | 0.965 | 0.979 | 0.989 | 0.998 | 0.997 | -0.942 | 1.000 | ||
| PC | -0.950 | -0.940 | -0.958 | -0.958 | -0.920 | -0.825 | 0.903 | -0.954 | 1.000 | |
| mp | 0.664 | 0.640 | 0.614 | 0.525 | 0.482 | 0.518 | -0.543 | 0.607 | -0.467 | 1.000 |
The correlations among the properties examined are shown in Table 8. As can be seen, most of the properties are highly correlated with one another, with the exception of mp, which is poorly correlated with the other properties. The remaining nine properties all have coefficients of determination greater than 0.82, and the subset of bp, MR, MV, and HV all have correlations greater than 0.90.
Table 9 gives the regression equations and the coefficients of determination (R2) values obtained by examining the relation between each property of the alkenes and ln(TG) separately. In Figure 3, the plot of boiling point values versus ln(TG) for the 161 alkenes studied can be seen for the representation of the acceptable scattering of the data.
Table 9. The regression equations and the coefficients of determination (R2) for the eleven properties of the alkene series obtained by the application of the index.
| regression equation | R2 | |
| bp (n=117) | y = 28.06x - 79.59 | 0.949 |
| MR (n=114) | y = 4.47x + 7.82 | 0.911 |
| MV (n=114) | y = 15.54x + 47.79 | 0.909 |
| HC (n=49) | y = 590.14x + 1079.51 | 0.940 |
| HV (n=27) | y = 4275.20x + 9208.43 | 0.903 |
| FLASH (n=14) | y = 14.83x + 173.78 | 0.806 |
| VIRC (n=11) | y = -663.95x + 1427.25 | 0.921 |
| TC (n=10) | y = 29.99x + 73.25 | 0.983 |
| PC (n=9) | y = -0.32x + 4.85 | 0.921 |
| mp (n=48) | y = 13.52x - 202.85 | 0.423 |
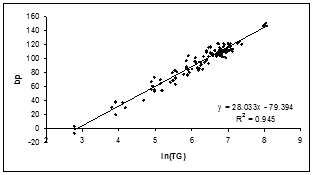
Figure 3. The plot of ln(TG) versus the boiling points of alkene derivatives (n = 117)
The regression equations presented in Table 9 are generally of high-quality for properties other than the mp. Therefore, property values estimated on the basis of these equations, with the exception of mp, should be sufficiently accurate for many practical purposes.
As can be seen from the table, the molecular mass/bulk clearly exerts the dominant influence on the properties other than mp, suggesting that dispersion forces play a dominant role for those properties which depend on intermolecular forces. A similar conclusion was reached in the earlier alkane study (see the previous part). This is a reasonable conclusion in the present case for bp, HV, VIRC, TC, PC, and VISC. For MV the ‘mass/bulk’ dependence can be attributed directly to the larger volume of compounds with higher number of carbon atoms. Likewise, MR depends largely on the higher number of electrons in larger compounds. For the two strictly "chemical" properties, the HC and the flashpoints (FLASH), the dependence on the mass/bulk dimension is more accurately attributed to the larger number of reacting bonds in the larger, higher number of carbon atoms containing compounds.
Branching, steric factors, and the double bond environment exert smaller influences on the properties, as demonstrated by the coefficients in the regression equations. Molecular branching sequesters interior parts of these compounds and reduces the extent of contact between neighboring molecules. The latter effect is reflected on the MVs. Because dispersion forces are strongly dependent on distance -the interaction energies fall as 1/r6, where r is the separation- a decrease in the amount of close contact decreases the cohesive forces experienced by the compounds. Therefore, bp and HV decrease as molecular branching increases.
The failure of the TG index to model the mp in this case is not surprising, either since this property was also not well modeled by these same topological parameters in the previous section, which deals with the alkanes. This illustrates the greater subtlety of the melting transition as compared to the boiling and critical transitions. The latter transitions involve a direct dependence on the operative intermolecular forces, and so directly reflect the strengths of these forces. The melting transition, in contrast, maintains a condensed phase and involves a partial disruption of intermolecular orientations. Melting, thus, depends on geometric factors, and other factors as well that are not well addressed by the present topological parameters (The TG index is directly influenced by the molecular shape and size.). This dependence on shape and entropic factors, in contrast to a simple intermolecular force dependence, is reflected in the melting point rather than the mass/bulk related factor. Dearden [37] has given a comprehensive review of mp predictions.
4. Conclusion
A novel toplogical index (TG Index) has been introduced and its application to some physical properties of alkanes and alkenes have been performed. TG Index is easy to calculate from the connectivity and distances of the chemical graph of a molecule. The correlation analysis of the index and the properties yielded quite reasonable data.
References
- N. Trinajstic, S. Nikolic, J.V. Knop, W.R. Müller, K. Szymanski, Computational Chemical Graph Theory, Simon and Schuster, Chichester, 1991.
- D.H. Rouvray, in Chemical Applications of Graph Theory, (Ed: A.T. Balaban) Academic Press, London, 1976, p. 175.
- J. Devillers, A.T. Balaban, Topological Indices and Related Descriptors in QSAR and QSPR. Gordon and Breach Science Publishers, Amsterdam, 1999.
- H. Kopp, Ann. Chem. Pharm. 50 (1844) 71-144.
- E. Heilbronner, The HMO Model and Its Application, Wiley, London, 1976.
- J. Devillers, A.T. Balaban, Topological Indices and Related Descriptors in QSAR and QSPR. Gordon and Breach Science Publishers, Amsterdam, 1999.
- F.S. Roberts, Discrete Mathematical Models. Prentice-Hall, CA, 1975.
- M. Barysz, D. Plavsic, N. Trinajstic, Math. Chem. 19 (1986) 89-116.
- D.E. Needham, I.C. Wei, P.G. Seybold, J. Am. Chem. Soc. 110 (1988) 4186-4194.
- R. Sayre, The Molar Refraction of Liquid Organosilicon Compounds. J. Chem. Eng. Data, 9 (1964) 146-153.
- K.G. Denbigh, Trans. Faraday Soc. 36 (1940) 936-948.
- A.I. Vogel, J. Chem. Soc. (1948) 1833.
- K.J. Miller, J.A. Savchic, J. Am. Chem. Soc. 101 (1979) 7206-7213.
- R.R.Driesbach, Physical Properties of Chemical Compounds, Advances in Chemistry 22, American Chemical Society, Washington DC, 1959.
- L. Pauling, D. Pressman, J. Am. Chem. Soc. 67 (1945) 1003-1003.
- W.J. Dunn, Eur. J. Med. Chem.-Chim.Ther.12 (1977) 109-112.
- P.V. Khadikar, D. Mandloi, A.V. Bajaj, S. Joshi, Bioorg. Med. Chem. Lett.13 (2003) 419-422.
- P.V. Khadikar, S. Karmarkar, J. Chem. Inf. Comput. Sci. 41 (2001) 934-949.
- H. Wiener, J. Am. Chem. Soc. 69 (1947) 17-20.
- L.N. Mulay, A. Weissberger, B. W. Rossiter, Techniques of Chemistry 4, Wiley-Interscience, New York, 1972, p. 431.
- R.E. Hoffman, J. Magn. Reson. 163 (2003) 325-331.
- http://en.wikipedia.org/wiki/parachor, August 2009.
- O. Exner, Nature, 196 (1962) 890-891.
- T. Sakka, Y.H. Ogata, J. Fluorine Chem. 126 (2005) 371-375.
- R.W. Taft, R.D. Topsom, Prog. Phys. Org. Chem. 16 (1987) 1.
- R.W. Taft, Prog. Phys. Org. Chem. 14 (1983) 247-350.
- R.W. Taft, I.A. Koppel, R.D. Topsom, F. Anivia, J. Am. Chem. Soc. 112 (1990) 2047-2052.
- D.E. Needham, I.C. Wei, P.G. Seybold, J. Am. Chem. Soc. 110 (1988) 4186-4194.
- A. Das, G. Domotor, I. Gutman, S. Joshi, S. Karmarkar, D. Khaddar, T. Khaddar, P.V. Khadikar, L. Popovic, N.S. Sapre, N. Sapre, A.A. Shirhatti, J. Serb. Chem. Soc. 62 (1997) 235-239.
- T. Zeljko, I. Gutman, J. Chem. Inf. Comput. Sci. 41 (2001) 1041-1045.
- G. Rücker, C. Rücker, J. Chem. Inf. Comput. Sci. 39 (1999) 788-802.
- R.H. Rohrbaugh, P.C. Jurs, Anal. Chem. 57 (1985) 2770-2773.
- P.J. Hansen, P.C. Jurs, Anal. Chem. 59 (1987) 2322-2327.
- S. Liu, R. Zhang, M. Liu, Z.J. Hu, Chem. Info. Comput. Sci. 37 (1997) 1146-1151.
- S.P. Verevkin, D. Wandschneider, A. Heintz, J. Chem. Eng. Data45 (2000) 618-625.
- S.D. Nelson, P.G. Seybold,J. Mol. Graph. and Model.20 (2001) 36-53.
- J.C. Dearden, in Advances in Quantitative Structure Property Relationships, (Ed: M. Charton), Vol. 2, J.A.I. Press, New York, 1999, pp. 127-175.



