Thermodynamic Properties and XAFS Debye Waller Factors of Metallic Nickel
Nguyen Van Hung1, *, Dinh Quoc Vuong2
1Department of Physics, College of Science, VNU-Hanoi, Nguyen Trai, Thanh Xuan, Hanoi, Vietnam
2Quang Ninh Education & Training Department, Nguyen Van Cu, Ha Long, Quang Ninh, Vietnam
Abstract
Thermodynamic properties and Debye-Waller factors of metallic Nickel described in terms of cumulant expansion up to the fourth order in X-ray absorption fine structure (XAFS) of metallic Nickel have been studied based on anharmonic correlated Debye model. Analytical expressions for dispersion relation, correlated Debye frequency and temperature, and four first XAFS cumulants have been derived which involve more information of phonons taken from integration over the phonon wave numbers varied in the first Brillouin zone. Derived anharmonic effective potential includes contributions of all nearest neighbors of absorber and backscattering atoms to take into account three-dimensional interaction and Morse potential parameters for describing single pair atomic interaction. Numerical results are found to be in good and reasonable agreement with experiment and with those of the other theories.
Keywords
Thermodynamic Properties, XAFS Debye-Waller Factor, Cumulant Expansion
Received: April 9, 2015 / Accepted: April 25, 2015 / Published online: May 15, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
XAFS (X-ray absorption fine structure) has developed into a powerful probe of atomic structure and thermal effects of substances [1-11]. According to cumulant expansion [1] the anharmonic XAFS function including anharmonic contributions of atomic vibration is given by [2]
![]() ,(1)
,(1)
where k and λ are the wave number and mean free path of emitted photoelectron, respectively, F(k) is the real atomic backscattering amplitude,![]() is net phase shift, N is atomic number of a shell,
is net phase shift, N is atomic number of a shell, ![]() is the intrinsic loss factor due to many-electron effects,
is the intrinsic loss factor due to many-electron effects, ![]() with
with ![]() as the instantaneous bond length between absorber and backscatterer atoms,
as the instantaneous bond length between absorber and backscatterer atoms, ![]() is its equilibrium value, and σ(n) (n = 1, 2, 3, 4 …) are the cumulants.
is its equilibrium value, and σ(n) (n = 1, 2, 3, 4 …) are the cumulants.
Hence, XAFS Debye-Waller factor is described in terms of cumulants, where the first cumulant is the net-thermal expansion, the second one describes the mean square relative displacement (MSRD), the third cumulant characterizes the phase shift and the fourth one contributes to XAFS amplitude. Then, the accurate cumulants are crucial to quantitative treatment of anharmonic XAFS spectra, so that the lack of the precise cumulants has been one of the biggest limitations to accurate structural determinations (e.g., the coordination numbers and the atomic distances) from XAFS experiment. Therefore, investigation of XAFS cumulants is of great interest.
Our development in this work is to derive a method for the calculation and analysis of the thermodynamic quantities and XAFS Debye-Waller factors described in terms of cumulant expansion up to the fourth order of metallic Nickel (Ni) having fcc structure based on the anharmonic correlated Debye model (ACDM). In Sect. 2, the analytical expressions for dispersion relation, correlated Debye frequency and temperature, first, second, third, and fourth cumulants of metallic Ni have been derived. The obtained cumulants contain more information taken from integration over the phonon wave numbers varied in the first Brillouin zone (BZ). Based on the success of the anharmonic effective potential used in the anharmonic correlated Einstein model (ACEM) [2-6] in XAFS theory due to taking into account three-dimensional interaction in a simple measures by including contributions of all nearest neighbors of absorber and backscattering atoms, in this work we develop further such anharmonic effective potential for higher expansion up to the fourth order. Numerical results for Ni (Sect. 3) are compared to experiment [7] and to those calculated using the other methods [3,8] which show good and reasonable agreement.
2. Formalism
2.1. High-Order Anharmonic Effective Potential
To determine Debye-Waller factors described in terms of cumulants, it is necessary to specify the interatomic potential and force constant [1-11]. Let us consider a high-order expanded anharmonic interatomic effective potential expanded up to the fourth order
![]() , (2)
, (2)
where ![]() is effective local force constant,
is effective local force constant, ![]() and
and ![]() are effective anharmonic parameters giving an asymmetry of the anharmonic effective potential, x is deviation of the instantaneous bond length between two immediate neighboring atoms r from its equilibrium value r0.
are effective anharmonic parameters giving an asymmetry of the anharmonic effective potential, x is deviation of the instantaneous bond length between two immediate neighboring atoms r from its equilibrium value r0.
The effective potential Eq. (2) is defined based on an assumption in the center-of-mass frame of single bond pair of absorber and backscatterer [3]. For monatomic crystals, the masses of absorber and backscatterer are the same so that it is given by
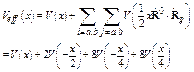 , (3)
, (3)
where the first term on the right concerns only absorber and backscatterer atoms, the remaining sums extend over the remaining neighbors, and the second equality is for fcc structure of Ni. Hence, this effective pair potential describes not only pair interaction of absorber and backscatterer atoms themselves, but also an affect of their near neighbors on such interaction. It is the difference of our effective potential from the single-pair (SP) [9] and single-bond (SB) [10] potentials which concern only each pair of immediate neighboring atoms, e.g., only V(x), without the remaining terms on the right of Eqs. (3).
A Morse potential is assumed to describe single-pair atomic interaction contained in the effective potential Eq. (3), and expanded up to the fourth order around its minimum
![]() , (4)
, (4)
where α describes the width of the potential, and D is dissociation energy.
Applying this Morse potential Eq. (4) to Eq. (3) and comparing the results to Eq. (2), we determine the coefficients ![]() of the anharmonic effective potential in terms of Morse potential parameters.
of the anharmonic effective potential in terms of Morse potential parameters.
2.2. Dispersion Relation, Correlated Debye Frequency and Temperature
In this work we generalize the pair model of Eq. (3) to that of a linear chain with the same effective potential in order to account for the effects of dispersion. Then, based on [12] for the case of vibration between absorber and backscattering atoms and using interatomic effective potential for fcc structure of Ni, the dispersion relation is expressed as
![]() , (5)
, (5)
where q is phonon wave number, M is mass of composite atoms, and a is lattice constant.
At the bounds of the first BZ of the linear chain, ![]() , the frequency has maximum so that we get the correlated Debye frequency
, the frequency has maximum so that we get the correlated Debye frequency ![]() and temperature
and temperature ![]() in the following form
in the following form
![]() , (6)
, (6)
where ![]() is Boltzmann constant.
is Boltzmann constant.
2.3. Four First XAFS Cumulants
We describe the parameter x in terms of the displacement of nth atom ![]() of the one dimensional chain as
of the one dimensional chain as
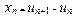 , (7)
, (7)
where the displacement ![]() are related to phonon displacement operators
are related to phonon displacement operators ![]() [13] by
[13] by
![]() ,
,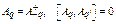 . (8)
. (8)
Applying ![]() from Eq. (8) to Eq. (7), the parameter
from Eq. (8) to Eq. (7), the parameter ![]() is given by
is given by
![]() . (9)
. (9)
In order to include anharmonic effects, Hamiltonian of the system is written in the summation of harmonic and anharmonic components, ![]() and
and![]() , respectively
, respectively
![]() , (10)
, (10)
where Ha consists of cubic Hc and quartic Hq term.
If anharmonic contribution to the anharmonic interatomic effective potential consists of the cubic term, then it can be expressed as
![]() , (11)
, (11)
or in the following form using Eq. (11) for the displacement of nth atom
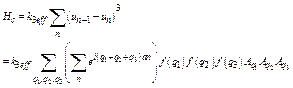 . (12)
. (12)
Comparing Eq. (12) to Eq. (11) and indicating
![]() ,
,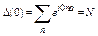 , (13)
, (13)
with N as the atomic number, we obtain
![]() . (14)
. (14)
Using Eq. (9) and Eq. (13), this Eq. (14) is changed into
![]() . (15)
. (15)
The first cumulant or net thermal expansion has been calculated with the aid of the many-body perturbation approach [14] using the expression
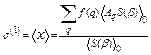 , (16)
, (16)
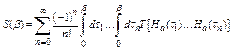 ,
, ![]() , (17)
, (17)
with taking backscattering only from the first shell.
Substituting into Eq. (16) the relations [14]
![]() ,
, 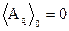 , (18)
, (18)
we obtain
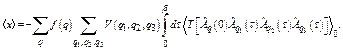 (19)
(19)
Using Wick theorem for T-product in the integral, the harmonic phonon Green function [14]
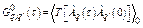 ,
, 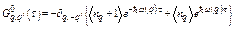 , (20)
, (20)
the symmetric properties of V(q1,q2,q3) [13], properties of function ![]() , the phonon density
, the phonon density
 , (21)
, (21)
as well as ![]() from Eq. (5), f(q) from Eq. (9),
from Eq. (5), f(q) from Eq. (9), ![]() from Eq. (13) and phonon momentum conservation in the first BZ, we change further Eq. (19) to the one in terms of Morse parameters
from Eq. (13) and phonon momentum conservation in the first BZ, we change further Eq. (19) to the one in terms of Morse parameters
 . (22)
. (22)
For large N, the summation over q can be replaced by the corresponding integral, so that the first cumulant has resulted as
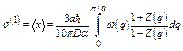 . (23)
. (23)
Now we calculate the second cumulant or MSRD ![]() in the form
in the form
 . (24)
. (24)
Using Eq. (5) for ![]() , Eq. (9) for
, Eq. (9) for ![]() and f(q), Eq. (13) for
and f(q), Eq. (13) for![]() and
and ![]() , Eq. (20) for
, Eq. (20) for![]() , and Eq. (17) for
, and Eq. (17) for![]() , we calculate
, we calculate ![]() to obtain the second cumulant in terms of Morse parameters
to obtain the second cumulant in terms of Morse parameters
![]() (25)
(25)
For large N, the summation over q can be replaced by the corresponding integral, so that the second cumulant is given by
 . (26)
. (26)
The third cumulant has been calculated using the following expression
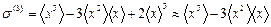 . (27)
. (27)
The calculation of ![]() is analogeous to the one of
is analogeous to the one of ![]() above, i. e.,
above, i. e.,
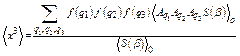 . (28)
. (28)
Using![]() from Eq. (17)with limiting only cubic anharmonic term,the Wick theorem for T- product and the symmetric properties of V(q1,q2,q3) [18], we calculated
from Eq. (17)with limiting only cubic anharmonic term,the Wick theorem for T- product and the symmetric properties of V(q1,q2,q3) [18], we calculated ![]() of Eq. (28). The product
of Eq. (28). The product ![]() has been calculated using
has been calculated using ![]() from Eq. (25) and
from Eq. (25) and ![]() from Eq. (22). Substituting the obtained
from Eq. (22). Substituting the obtained ![]() and
and ![]() into Eq. (28) with application of the relation for phonon momentum conservation in the first BZ, we obtain the third cumulant in terms of Morse parameters as
into Eq. (28) with application of the relation for phonon momentum conservation in the first BZ, we obtain the third cumulant in terms of Morse parameters as
![]() (29)
(29)
For large N, the summation over q can be replaced by the corresponding integral, so that the third cumulant is given by
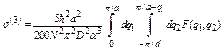 , (30)
, (30)
![]() (31)
(31)
For calculation of the fourth cumulant, the Hamiltonian of the system includes anharmonic contributions up to the fourth order, so that similar to Eq. (12) we obtain
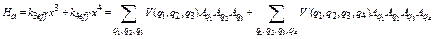 , (32)
, (32)
 . (33)
. (33)
The fourth cumulant has been calculated based on the following expression
![]() . (34)
. (34)
The calculation of ![]() is analogous to the one of
is analogous to the one of ![]() above, and using
above, and using ![]() from Eq. (25) we obtain
from Eq. (25) we obtain ![]() . Substituting these values into Eq. (34) and using the phonon momentum conservation in the first BZ, the fourth cumulant Eq. (34) in terms of Morse parameters has resulted as
. Substituting these values into Eq. (34) and using the phonon momentum conservation in the first BZ, the fourth cumulant Eq. (34) in terms of Morse parameters has resulted as
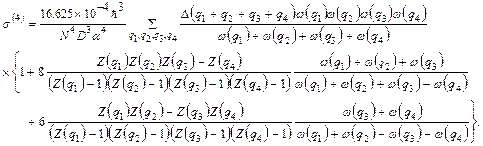 (35)
(35)
For large N, the summation over q can be replaced by the corresponding integral, so that the fourth cumulant Eq. (35) is given by
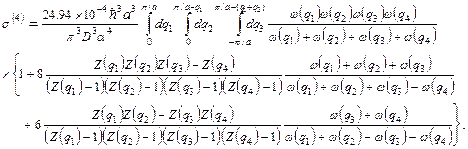 (36)
(36)
3. Numerical Results and Discussions
Now we apply the expressions derived in the previous sections to numerical calculations for metallic Ni having fcc structure. We use the Morse parameters D = 0.4203 eV, α = 1.4199 Å-1 [15] which were obtained using experimental values for the energy of sublimation, the compressibility, and the lattice constant, as well as its measured Morse parameters (MMP) D = 0.41 eV, α = 1.39 Å-1 [7]. They have been used for calculating the effective local force constant keff, correlated Debye frequency ![]() and temperature
and temperature ![]() of Ni. The results are written in Table 1 compared to the experimental values [7] which show reasonable agreement.
of Ni. The results are written in Table 1 compared to the experimental values [7] which show reasonable agreement.
Fig. 1 illustrates good agreement of the anharmonic effective potential (Fig. 1a) and dispersion relation (Fig. 1b) of Ni calculated using the present theory compared to those obtained from its MMP [7]. The anharmonic effective potential (Fig. 1a) is shifted from the harmonic term to be asymmetric due to including the anharmonic effects, and the maximal frequencies ω(q) (Fig. 1b) at ![]() are equal to the Debye frequencies of Ni written in Tab. 1.
are equal to the Debye frequencies of Ni written in Tab. 1.
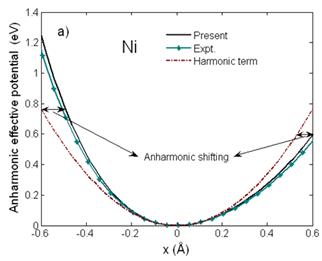
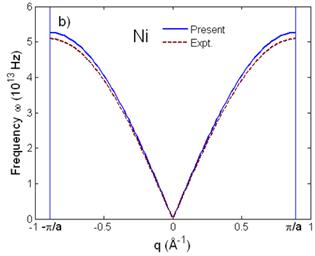
Fig. 1. a) Anharmonic effective interatomic potential and b) dispersion relation of Ni calculated using the present theory compared to experiment (Expt.) obtained from its MMP [7].
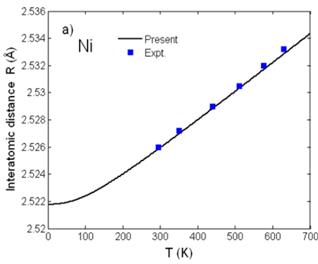
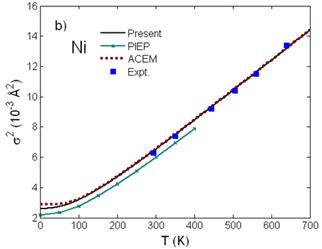
Fig. 2. Temperature dependence of a) interatomic distance R(T) and b) second cumulant σ2(T) of Ni calculated using the present theory compared to the experimental values [7] and to those calculated using ACEM [3] and PIEP [8] for σ2(T).
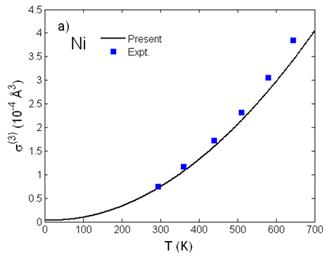
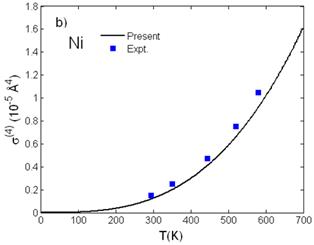
Fig. 3. Temperature dependence of a) third cumulant σ(3)(T) and b) fourth cumulant σ(4)(T) of Ni calculated using the present theory compared to the experimental values [7].
Table 1. The values of ![]() for Ni calculated using the present theory compared to the experimental values [7].
for Ni calculated using the present theory compared to the experimental values [7].
| Quantities | |||
| Ni, Present | 67.9150 | 5.2637 | 376 |
| Ni, Expt. [7] | 63.4596 | 5.0881 | 378 |
Fig. 2 shows good agreement of the interatomic distance R(T) = R(0) + σ(1)(T) (Fig. 2a) obtained from the first cumulant σ(1)(T) or net thermal expansion and of the second cumulant σ2(T) or MSRD (Fig. 2b) of Ni calculated using the present theory with the experimental values [7] and with those calculated using the ACEM [3] and the path-integral effective potential (PIEP) method [8]. Further, reasonable agreement with the experimental values [7] at different temperatures has been presented for the third cumulant σ(3)(T) (Fig. 3a) and for the fourth cumulant σ(4)(T) (Fig. 3b) of Ni calculated using the present theory. Moreover, all the numerical results show that at high-temperature the first and second cumulants are linear to the temperature T, the third and fourth cumulants vary as T2 and T3, respectively, as it was obtained in the other theories [11], and at low-temperature, they contain zero-point energy contributions, a quantum effect.
4. Conclusions
In this work, a method has been derived for the calculation and analysis of the thermodynamic parameters and high-order expanded XAFS Debye-Waller factors described in terms of cumulants of metallic Ni based on the anharmonic correlated Debye model with considering dispersion relation to take more information of phonons taken from integration over the phonon wave numbers varied in the first BZ and the anharmonic effective potential involving the contributions of all nearest neighbors of absorber and backscattering atoms to take into account three-dimensional interaction. Morse potential is used for describing the single-pair interatomic interaction. Moreover, since Ni has fcc structure, the present derived theory can also be generalized to study other metals having the same this crystal structure.
Derived analytical expressions for the anharmonic interatomic effective potential, dispersion relation, correlated Debye frequency and temperature, as well as four first XAFS cumulants satisfy all their fundamental properties showing that at high-temperature the first and second cumulants are linear to the temperature T, the third and fourth cumulants vary as T2 and T3, respectively, and at low-temperature they contain zero-point energy contributions, a quantum effect.
The good and reasonable agreement of numerical results for metallic Ni with experiment and with those calculated using the other theories illustrates the advantage and efficiency of the present theory and of using the anharmonic effective potential in XAFS data analysis.
Acknowledgements
The authors thank Prof. J. J. Rehr and Prof. P. Fornasini for useful comments.
References
- Crozier E. D., Rehr J. J, and Ingalls R.X-ray Absorption. edited by D. C. Koningsberger andR. Prins (Wiley, New York, 1988).
- Hung N. V., Duc N. B., Frahm R. R. A New Anharmonic Factor and EXAFS including Anharmonic Contributions. J. Phys. Soc. Jpn. 2003; 72: 1254.
- Hung N. V. and Rehr J. J. Anharmonic correlated Einstein model Debye-Waller factors. Phys. Rev. B 1997,56: 43.
- Daniel M., Pease D. M., Hung N. V., Budnick J. D. Local force constants of transition metal dopants in a nickel host: Comparison to Mossbauer studies. Phys. Rev. B 2004; 68: 134414.
- Hung N. V., L. H. Hung L. H., Tien T. S., Frahm R. R.Anharmonic Effective Potential, Local Force Constant and EXAFS of HCP Crystals: Theory and Comparison to Experiment. Int. J. Mod. Phys. B 2008; 22: 5155.
- Hung N. V. Pressure-Dependent Anharmonic Correlated XAFS Debye-Waller Factors. J. Phys. Soc. Jpn. 2014; 83: 024802.
- Pirog I. V., Nedoseikina T. I., Zarubin A. I., Shuvaev A.T. Anharmonic pair potential study in face-centered cubic crystals. J. Phys.: Condens. Matter 2002; 14: 1825.
- Yokoyama T. Path-integral effective-potential method applied to extended x-ray-absorption fine-structure cumulants. Phys. Rev. B 1998; 57: 3423.
- Miyanaga T.,Fujikawa T. Quantum Statistical Approach to Debye-Waller Factor in EXAFS, EELS and ARXPS. III. Application of Debye and Einstein Approximation" J. Phys. Soc. Jpn. 1994; 63: 3683.
- Frenkel A. I. and Rehr J. J. Thermal expansion and x-ray-absorption fine-structure cumulants. Phys. Rev. B 1993; 48: 585.
- Stern A., P. Livins, and Zhe Zhang. Thermal vibration and melting from a local perspective Phys. Rev. B 1991; 43: 8850.
- Kittel C. Introduction to Solid State Physics. (John-Wiley&Sons, Inc., New York, 1986), 6th ed.
- Maradudin A. A. Dynamical Properties of Solids. ed. by Horton G. K. and Maradudin A. A. (North Holland, Amsterdam, 1974) Vol. 1, p. 1.
- G. D. Mahan G. D. "Many-Particle Physics" (Plenum, New York, 1990) 2nded.
- Girifalco L. A. and Weizer W. G. Application of the Morse Potential Function to Cubic Metals. Phys. Rev. 1959; 114: 687.



