The Simultaneous Reduction of Matrices to the Block-Triangular Form

Yuri N. Bazilevich^*

Department of Applied Mathematics, Prydniprovsk State Academy of Civil Engineering and Architecture, Dnipropetrovs'k, Ukraine

Abstract

The solution of the problem of several n´n matrices reduction to the same upper block-triangular form by a similarity transformation with the greatest possible number of blocks on the main diagonal is given. In addition to the well-known "method of commutative matrix" a new "method of invariant subspace" is used.

Keywords

Matrix, Block-Triangular Form, Similarity Transformation, the Centralizer, Algebra over the Field, Radical Ideal

Received: July 10, 2015
Accepted: July 25, 2015
Published online: August 8, 2015

@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/

1. Introduction

At first, let us consider the case when the number of matrices d = 2.

    (1)

There are two square matrices B₁ and B₂ over the field  of complex numbers. We need to find the similarity transformation (1) reducing both matrices to the equal block-triangular form. Here  is a block of matrix B_n located in the i-th column and j-th row of this partitioned matrix. The diagonal blocks must be square submatrices.

It is necessary that the number l of diagonal blocks to be the maximum possible.

The idea of the method was published in the author's monograph [1]. Corresponding computational algorithms and results of calculations on handling of applied problems are presented in papers [2,3]. In this paper a detailed theoretical basis of the developed methods is given.

There exists a solution for the case of only one matrix. One matrix can be reduced to its Jordan form. There is a famous unsolved problem — to create a canonical form for a pair of matrices. This problem and the equivalent problems are called wild problems [4].

2. The General Calculation Scheme

We use the "method of commutative matrix" and the "method of invariant subspace." The first one allows you to find the similarity transformation, reducing both matrices to a block-diagonal form with two (at least) blocks on the main diagonal, or to determine that such reduction is impossible for these matrices. The other method is intended to reduce such two matrices that are not reduced to the block-diagonal form, to a block-triangular form, or to determine that they cannot be reduced to a "strict" block-triangular form either. There is also used a method of overcoming the special case (see Section 6).

This approach is consistently applied firstly to the initial pair of matrices, then to pairs of blocks that appear on the main diagonal. The process continues until we obtain the pairs of blocks that are irreducible to the same block-triangular form. From the uniqueness theorem it follows that this approach gives the solution of the problem.

3. The Method of Commutative Matrix

Possibility of application of commutative matrix for decoupling of system of equations was described in the textbooks on quantum mechanics (for example, see the book by Fermi [5]). The method of commutative matrix as such was proposed simultaneously by A.K. Lopatin [6] and E.D. Yakubovich [7].

Let us consider  set of all matrices that are commutative with matrices B₁, B₂. This set is an algebra over the field  of complex numbers. is called a centralizer of matrices {B_n}.

Theorem 1. Let matrices A and X be commutative:

AХ = ХA,

matrix X has the block-diagonal form of , where the spectra of the blocks are mutually disjoint. Then the matrix А also has the block-diagonal form

А = diag.

This theorem is given in [8] — Ch. VIII, Theorem 3. See also [1] § 2.5.

Corollary. Let a matrix  exist, having at least two different eigenvalues. Let the column of matrix S be the vectors of canonical basis of matrix X. Then similarity transformation  reduces both matrices to the block-diagonal form with two (at least) blocks on the main diagonal.

Proof. Property of matrices commutation is preserved under the similarity transformation. Indeed:

,

where  S is the non-singular matrix.

Let the matrix X have at least two different eigenvalues and commute with matrices B₁, B₂ and let the columns of the matrix S be the vectors of the canonical basis of the matrix X. In this case the transformation  reduces matrix X to its Jordan form. Therefore, , where X₁ is a Jordan block corresponding to the first eigenvalue of the matrix X, and X₂ — to the second and the subsequent (if any) eigenvalues. Both blocks are not empty and they have no common eigenvalues. The matrices  commute with the matrix. From Theorem 1 it follows that they have the block-diagonal form.

Theorem 2. If matrices B_n are reduced to the block-diagonal form with two (at least) blocks on the main diagonal by similarity transformation, then there exists a matrix  with at least two different eigenvalues.

Proof. Let. Let us compose the matrix, where E₁ and E₂ are the identity matrices. Matrix  commutes with B_n and has two different eigenvalues l₁ = 1, l₂ = 2.

So, for the simultaneous reduction of two matrices to the block-diagonal form it is necessary and sufficient that the centralizer of the matrix to contain the matrix X with different eigenvalues.

To find the centralizer (or more precisely — its basis), you can declare all the elements of the matrix X as unknown numbers and create a system of linear homogeneous algebraic equations corresponding to the matrix equations

B₁Х = ХB₁,   B₂Х = ХB₂.                     (2)

We have 2n² equations with n² unknowns. If n is small, then general solution of this system of equations can be made by known methods. Computing method of coping with large n is given in [9].

Let W₁, W₂,…, W_r matrices form a basis of centralizer Λ(B_n). If the rank r of the centralizer is equal to 1, then the whole centralizer consists of only matrices that are multiple of the identity matrix. In this case, a reduction of matrices B_n to the block-diagonal form is impossible. If r > 1, then among the matrices W_k we choose a matrix X that has at least two different eigenvalues.

We draw up a matrix of similarity transformation of the column-vectors of the canonical basis of the matrix X.

The special case, where r > 1, but all matrices of the basis do not have different eigenvalues, is discussed below (see Section 6).

4. The Method of Invariant Subspace

The idea of the method is proposed in [1] (Chapter 7).

Let us consider matrices B_n (n = 1, 2) that are not reduced simultaneously to the block-diagonal form. Otherwise we would have already done it by the method of the commutative matrix. We want to find out, whether they could be reduced to the block-triangular form.

4.1. Construction of Algebra

The first step of the method is the construction of algebra with unit  generated by the initial matrices. You can do as follows [2]: firstly, we choose linearly independent elements of the matrix {E, B₁, B₂} and call them "assumed basis". Then we consider all the possible products of these matrices. If the next product does not belong to the linear span of the "assumed basis", we add it to this set and consider the elements products of a new "assumed basis". We continue this process until none of the products goes beyond the linear span. The indication that the element does not belong to the linear span of the "assumed basis" is that the addition of a new element gives a linearly independent set of elements. Verification of linear independence is possible using program SLAU5 [1].

The possibility of matrices reduction to the block-triangular form is equivalent to the reducibility of algebra. The criterion of reducibility of algebra: the rank of the algebra j(В_n) is smaller than n², where n is matrices order. This follows from the Burnside theorem [10] (see also [6], Theorem 1 ').

4.2. Calculation of an Algebra Radical Ideal

Theorem 3. If rank r of algebra j(В_n) is smaller than n² and if centralizer Λ(B_n) does not contain any matrix X with different eigenvalues, then the algebra j(В_n) is non-semisimple.

Proof. The condition r < n² means that the algebra j(В_n) is reducible [10,11]. A reducible algebra may be semisimple or non-semisimple. Algebra is not semisimple because the matrices (including {B_n}) are not reducible to the block-diagonal form (if only they were reducible, we could do this by the method of commutative matrix). Therefore the algebra is non-semisimple.

A non-semisimple algebra has a nontrivial radical ideal. There are formulas to find it [11]: the coordinates a = [a₁, a₂, …, a_r]^т of any radical ideal element in the basic set of the algebra satisfy the equation

Da = 0,   D = {d_ij},                                (3)

where d_ij = Sp(W_i W_j), Sp(.) is the trace of matrix. {W_i} is the basic set of the algebra.

The general solution of equation (3) can be obtained by known methods. You can, for example, use the program SLAU5 [1]. Consequently, it is possible to obtain a basis of radical ideal.

4.3. Finding of Invariant Subspace

Let Z-set be intersection of all kernels of radical ideal elements of the algebra j(В_n). We can find Z-set (its basis) as a general solution of the corresponding system of algebraic equations.

Theorem 4. Z-set is a subspace of space .

Proof. This set can be found with only elements of the basis. The calculation corresponds to finding a solution of the system of linear homogeneous algebraic equations. The general solution of this system, as we know, is a subspace.

Theorem 5. If algebra is non-semisimple, then Z-set is a nontrivial subspace.

Proof. In this case, a non-zero radical ideal is a set of matrices , where t is the parameters vector. The radical ideal is a nilpotent subalgebra because all its elements are nilpotent (see [11, § 7, Theorem 2]). Hence, ,  . Let   be nonzero matrix of the set , and  — its nonzero column. Then , since . So, the equation  has nontrivial solutions.

Theorem 6. The subspace Z-set is an invariant with respect to the matrices {B_}.

Proof. Radical ideal  of algebra j(В_) is its ideal. Matrices  are members of algebra j(В_). Hence, we obtain where , i.e. Z-set is invariant with respect to the set of matrices {B_i}.

Thus, for the case when the matrices are not reduced to the block-diagonal form, but the rank of the algebra j(В_n) is less than n², we have a method of construction of nontrivial subspace that is invariant with respect to these matrices.

4.4. Construction of the Transformation Matrix

Theorem 7. The simultaneous reduction of a pair of matrices to the block-triangular form is possible if and only if there exists a nontrivial invariant with respect to both matrices subspace .

Proof. . Let

where  are matrices of order m. Then the set of vectors , where , is invariant with respect to matrices , i.e. if   then .  Let V consist of all vectors of the form , . From the invariance of the matrices, it follows that. Therefore,

 .

 Suppose there exists a nontrivial subspace V that is invariant with respect to the matrices . Let  be a basis of the subspace V. Let  be its addition to the basis of . Let the columns of matrix S be the vectors . From the rules of matrix multiplication, it follows that the equality is an equivalent to similarity transformation ,  and this equality can be written as

,                             (4)

where  are the elements of the matrix ,  A is an arbitrary matrix.

The condition of invariance of the subspace V means that any element of the basis  after multiplication by any of the matrix  remains in the subspace V and, therefore, is a linear combination of elements:

.

Comparing the last equality with (4) and taking into account the linear independence of vectors, we obtain, . These equations are performed at all. Consequently, the corresponding elements of matrices  are equal to zero, i.e. modified matrices have the block-triangular form.

We form the transformation matrix S from the basis vectors of this subspace and a subspace being a direct complement to it. We locate vectors as columns (see the proof of Theorem 7).

Direct sum to the subspace can be found as a general solution x of the linear homogeneous algebraic equations

.

Here, T is a sign of transposition.

To find the general solution, you can use the program SLAU5 [1].

5. The Uniqueness Theorem

There is the uniqueness theorem.

Theorem 8. Let the matrices , i = 1, 2, be reduced to the block-triangular form

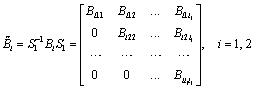
by some similarity transformation and further reduction for each pair of blocks {B_1kk, B_2kk} is impossible. If there exists another similarity transformation such that for the resulting blocks further reduction is impossible:

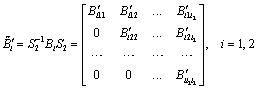
then  and we can determine the correspondence between the numbers of blocks such that the blocks B_ikk are similar to blocks .

Proof. This theorem follows from Theorem of Jordan — Holder (see, also [12], Theorem 1).

6. Special Case

Let us consider the case when the basis of the centralizer contains more than one matrix (r > 1), but each of these matrices has no different eigenvalues. There is an assumption that in this case all the matrices of the centralizer have no different eigenvalues and, accordingly, the initial matrices are not reduced to the block-diagonal form simultaneously. It turns out that this assumption is valid if the algebra  has a rank r ≤ 3 and is not valid if rank r = 4 (see [1], Theorem 6.6).

This Section shows how in this case to reduce the matrices to the block-triangular form, without discussing the possibility of reducing them to the block-diagonal form.

Theorem 9. If the rank of the centralizer  of the matrices  is greater than one: r >1, then the matrices  are reduced to the block-triangular form.

Proof. Let W₁,…, W_r be the basis of algebra  and W₁=E. If W₂ matrix have two (or more) different eigenvalues, then we can reduce initial matrices to the block-diagonal form by method of commutative matrix. Otherwise eigenvalue  is unique. Therefore matrix  is nilpotent. Matrix G is nilpotent and nonzero, therefore subspace  is nontrivial. Besides , i.e. subspace L is invariant with respect of matrices . Consequently, we can reduce matrices  to the block-triangular form in this case too (Theorem 7).

We need to create a matrix  and find the vectors  as the basis of kernel matrix G to construct the transformation matrix S. Further construction is the same as in Subsection 4.4.

Note. The condition  is not necessary to reduce the matrices to the block-triangular form.

7. Examples

7.1. The First Example

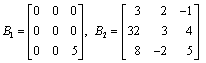 (see [1], example 1.6).

We use the method of commutative matrix. All the elements x_ij of matrix X are considered as unknown. We constitute a system of algebraic equations corresponding to the matrix equations B₁Х = ХB₁, B₂Х = ХB₂. Its general solution is as follows:

where x₁₁ and x₂₁ are free unknowns. Or in other way

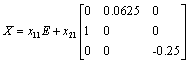
If x₁₁ = 0, x₂₁ =1 the eigenvalues of X are: l₁ = l₂ = – 0.25;  l₃ = 0.25. Then we obtain eigenvectors of matrix X and build the transformation matrix

The initial matrix is reduced to the block-diagonal form:

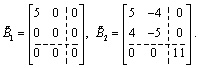                         (5)

Next, we consider the blocks  For them a set of commuting matrices  is aE, where a is an arbitrary number. So reduction of these blocks to the diagonal form is impossible (Theorem 2). We verify the possibility of reducing by the method of invariant subspace. Matrices E, B₁₁₁ and B₂₁₁ are linearly independent. Products of any of these matrices to the identity matrix E belong to the linear span of the first three matrices. Matrix  is a member of this set too. We consider the product U = B₁₁₁ B₂₁₁. Using the equality aE + b B₁₁₁ + g B₂₁₁ + l U = 0 we obtain: a = b = g = l = 0, i.e. matrix U does not belong to the linear span of the first three matrices. We obtain that r = 4 and the condition r < n² is not performed.

Further simplification of the matrices is impossible (see Subsection 4.1). Therefore the final result is the matrices (5).

7.2. The Second Example

,  (see [1], example 7.3).

Direct verification shows that the corresponding centralizer consists only of matrices . Therefore, reduction of matrices  to diagonal form is impossible.

Let us build algebra . Matrices E, B₁, B₂ are linearly independent. Let us denote these matrices W₁, W₂, W₃ respectively. Let us consider all possible products of matrices W_kW_j and verify whether the resulting matrices are the linear combination of the original. Since multiplication by W₁ = E does not change the matrices, we consider products W_kW_j for k, j = 2, 3. We compute: . We verify whether the matrix is the linear combination of the first two ones: . This equation corresponds to the system of equations. Its solution is: β = 3, a = – 2. Consequently, the matrix is a linear combination of the matrices W₁ and W₂. Next, we calculate:

We have found that all products belong to the linear span of the matrices W₁, W₂, W₃. Consequently, these matrices form the basis of algebra . The number of elements of the basis r = 3, i.e. . This means that the reduction to triangular form is possible.

Let us compose the matrix D = {Sp(W_jW_k)}. All products W_jW_k are already calculated. We obtain

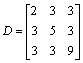
Let us form the system of equations Da = 0. The general solution of this system includes: a₁ = –6a₃, a₂ = 3a₃, where a₃ is a free variable. Let a₃ = 1. We obtain. We compute the matrix G: The equations  are of the form:  Hence: . We put: . Therefore, the basis of Z-set consists of one vector: . This vector and the vector  are linearly independent. Therefore: . Then we obtain

; ;

;

7.3. The Third Example

. These matrices describe the motion of the system from [13].

It is clear, that we can reduce the matrix B₂ to its Jordan form. But let us consider the approach set forth above.

Let us find matrix X that commutes with the initial matrices. As a result of calculations we obtain: X = aE, where a is an arbitrary parameter. Since matrix X has no different eigenvalues, reduction of the initial matrices to the block-diagonal form is impossible.

Next, we use the method of invariant subspace.

We act as in the previous example. We obtain: r = 2. The condition  is performed. Next: D = .

The system of equations Dy = 0 takes the form: 2y₁ + 2y₂ = 0, 2y₁ + 2y₂ = 0. As a result, we obtain: y = . Basis of radical ideal is a matrix G:

.

Equation Gx = 0 takes the form: x₁ – x₂ = 0,  x₁ – x₂ = 0. The basis of general solutions of the system consists of the vector . This vector and the vector  are linearly independent. Therefore, . We obtain the triangular matrices:

, .

Peculiarity of this example is that here exists a non-compact group of matrices commuting with the initial matrices.

8. Generalizations

The problem of getting the best block-triangle form can be formulated in another way: to find a transformation matrix S such that the maximum of the orders of the diagonal blocks will be the lowest possible. The uniqueness theorem implies that by solving the problem of getting the maximum number of blocks we simultaneously obtain the block having the lowest possible order.

It is clear that there can be more than two initial matrices. In this case course of solution will have no changes. Only the number of matrix equations (2) or the amount of the initial matrices for composition of the algebra j(В_n) will be increased.

Let us consider the problem of reduction of matrices  to the block-triangular form by transformation , where H and S are non-singular square matrices. This transformation is more effective than the similarity transformation (1). The problem is solved in the case, where one of the initial matrices is nonsingular.

Next, we need Theorem 10 by A.K. Lopatin. Refined formulation and proof of the result is as follows (see [1], Theorem 7.4).

Theorem 10. There exists a similarity transformation reducing matrix  to the block-triangular form with l blocks on the main diagonal if and only if there exists a set of matrices  such that

,

,        (6)

where .

Proof.  Let matrices  be block-triangular. Let blocks  on the main diagonal be of the order  and . We choose a set of matrices  in the form , where the matrices  have the same kind of block as ; all the blocks of the variable matrices  standing above the main diagonal are filled with parameters , and other elements of this matrix are zero. Then

,

where .

It is clear that . After the transformations , ,  this equality is still valid.

 The condition  means that , i.e. a subspace  is invariant with respect to the matrix .

Let us denote  as the number of blocks on the main diagonal of the matrices  reduced to the block-triangular form. Let

.

Theorem 11. Let  be matrices. If , then , where N is any non-singular matrix.

Proof. Let  and  be the transformation matrices, whereby the initial matrices  are reduced to the block-triangular form by formula  and have the maximum possible number of blocks on the main diagonal. In this case matrices  have the same block-diagonal form. According to Theorem 10, there must be the matrices  such that

,

, ,

where .

Let us perform a similarity transformation , , and replacement of vectors  into . Equations (6) are retained. Moreover, :

.

Using Theorem 10, we obtain .

For finding a transformation  with the greatest possible number of blocks on the main diagonal it is sufficient to solve this problem by a similarity transformation for supportive matrices , , .

9. Conclusion

Thus, the problem is completely solved. A method to bring a set of matrices to the best block-triangular form has been developed.

This result is of practical significance. This method can simplify a system of linear differential equations containing several matrices of coefficients [1,14]. Equations decoupling to independent subsystems corresponds to reducing matrices to the block-diagonal form. Reduction of matrices to the block-triangular form corresponds to "hierarchic" (vertical) decoupling. Thus, first subsystem does not contain variables of other subsystems. Only variables of the first and the second subsystems are present in the second subsystem, etc. The number of such subsystems can be greater than at ordinary decoupling.

10. Next Directions of Investigation

It would be helpful to solve the following problems as well.

• The solution of the same problem for matrices over other fields (real numbers, rational numbers, etc.).

• More detailed study of the special case is considered in Section 6.

• Using the transformation  without requiring non-singularity of one of the matrices.

• Reduction to the best block-triangular form nn-matrix A and nn-matrix m-matrix B by transformation. Here S₁ and S₂ are nonsingular square matrices of corresponding orders. This problem and others, similar to it, are necessary for the hierarchic decoupling of systems of equations with rectangular coefficient matrices (see [1] Сhapter 8 and [12]).

References

1. Bazilevich Yu.N.,Numerical decoupling methods in the linear problems of mechanics, Kyiv, Naukova Dumka, 1987 (in Russian).
2. Bazilevich Yu.N., Korotenko M.L. and Shvets I.V.,Solving the problem on hierarchical decoupling the linearmathematical models of mechanical systems,Tekhnicheskaya Mekhanika, 2003, N 1, 135–141 (in Russian).
3. Bazilevich Yu.N.,The exact decoupling of linear systems,Electronic Journal "Issledovano v Rossii", 2006, 018, 182–190, http://www.sci-journal.ru/articles/2006/018.pdf(in Russian).
4. Drozd Yu. A.,Tame and wild matrix problems, Lect. Notes Math., 832, 242-258 (1980).
5. Fermi Enrico,Notes on quantum mechanics/ The University of Chicago Pres
6. Lopatin A.K.,The algebraic reducibility of systems of linear differential equations. I,Diff. Uravn., 1968,V.4, 439–445 (in Russian).
7. Yakubovich E.D.,Construction of replacement systems for a class of multidimensional linear automaticcontrol systems,Izv. Vuzov, Radiofizika, 1969, V.12, N 3, 362–377 (in Russian).
8. Gantmacher F. R.,The Theory of Matrices / Chelsea: New York. 1960.
9. Bazilevich Yu.N., Buldovich A.L.,Algorithm for finding the general solution of the system of linear homogeneous algebraic equations in the case of very large-scale sparse matrix coefficients // Mathematical models and modern technology. Coll. scientific. tr. / NAS. Institute of Mathematics. - Kyiv, 1998. — 12, 13(inRussian).
10. Van Der WaerdenAlgebra.vols.IandII. Springer-Verlag.
11. Chebotariov N.G.,Introduction to theory of algebras, Moscow: Editorial URSS, 2003 (inRussian).
12. Belozerov V.E., Mozhaev G.V.,The uniqueness of the solution of problems of decoupling and aggregation of linear systems of automatic control // Teoriya slozhnyih sistem i metodyi ih modelirovaniya.— M: VNIISI, 1982.—4-13(inRussian).
13. Bazilevich Yu.N.Hidden Symmetry Exposure. The Mechanical Systems with the Hard Structure of Forces// Proceedings of Institute of Mathematics of NAS of Ukraine. — V. 50. — Part 3. — Kyiv: Institute of Mathematics of NAS of Ukraine, 2004 /—P.1261—1265.
14. Pavlovsky Yu.N., Smirnova T.G.,The problem of decomposition in the mathematical modeling.— M .: FAZIS, 1998. VI + 266(inRussian).