Effect of Localized Wall Heating/Cooling on the Unsteady MHD Decelerating Flow over a Wedge
C. Poornima1, *, A. T. Eswara2
1Department of Mathematics, P.E.S. College of Engineering, Mandya, India
2Department of Mathematics, GSSS Institute of Engineering and Technology for Women, Mysore, India
Abstract
The present paper investigates the effect of localized wall heating/cooling on the unsteady, MHD laminar boundary layer decelerating forced flow of an incompressible electrically conducting fluid over a wedge. The set of non-linear partial differential equations governing the semi-similar flow has been solved numerically using an implicit finite difference scheme along with the quasilinearization technique. Numerical computations has been carried out and the results are presented graphically to show the effect of various physical parameters such as unsteady parameter, magnetic parameter, wall heating/cooling parameter on the flow field and heat transfer characteristics. It is found that the dual solutions exist for critical values of the unsteady parameter. Further, the magnetic field plays a significant role in controlling the boundary layer separation.
Keywords
Unsteady Decelerating Flow, Semi-Similar Solution, Localized Wall Heating (Cooling), Skin Friction, Heat Transfer
Received: July 6, 2015
Accepted: July 23, 2015
Published online: August 5, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
The study of laminar boundary layer flows is always important from the view point of engineering and technology. The two-dimensional incompressible laminar boundary layer flow passing over a wedge was first introduced by Falkner and Skan [1]. In the past few years several investigations [2-10] have been reported in the literature focusing on this topic using various methods which is suitable for the flow and heat transfer phenomena. In recent years, the application of a transverse magnetic field on boundary layer flow control has made a great impact in the study of magnetohydrodynamic (MHD) flow and heat transfer problems having technological applications in modern metallurgical and metal-working processes. MHD effects on the Falkner-Skan wedge flow are studied by Kafoussias [11] and Devi [12].
In forced convection laminar boundary layer flow over a wedge, the pressure gradient parameter tends to increase the skin friction as well as heat transfer. However, it is possible to reduce the skin friction and heat transfer by localized heating/cooling of the surface. The process of localized wallheating/cooling (in which a certain portion of the wall is being heated or cooled while the remaining portion is unchanged) s of vital importance for various scientific and technological potential applications including the controlling of the laminar boundary layer flow separation. The heated surface can also be cooled by removing the heat source from the localized slots on the surface. Indeed, localized wall heating/cooling promotes energizing of the inner portion of boundary layer in adverse pressure gradient and plays a key role in boundary layer control [13,14]. In spite of its several applications, there are only few papers in the literature that deals with localized wall heating/cooling. Chamkha et. al [15] have studied the mixed convection flow over a vertical flat plate with localized wall heating(cooling) including the effects of magnetic field, suction and injection. Kumari and Nath [16] have investigated the mixed convection flow over a thin vertical cylinder with localized suction/injection and wall heating/cooling. Recently, Poornima and Eswara [17] have considered steady, MHD Falkner-Skan flow over a wedge with localized wall heating (cooling).
The main purpose of the present paper is to discuss the unsteady laminar boundary layer forced convection decelerating flow of an electrically conducting fluid over a sharp wedge in the presence of a transverse magnetic field with localized wall heating/cooling. The nonlinear parabolic partial differential equations governing the semi-similar flow have been solved numerically using an implicit finite difference scheme along with quasilinearization technique. The present analysis may be useful in industrial applications dealing with controlling as well as stabilization of the boundary layer. It may be mentioned here that the counter part of the present investigation pertaining to the accelerating flow has been studied more recently by Poornima and Eswara [18].
2. Mathematical Analysis
Consider the unsteady, two-dimensional laminar boundary layer forced convection flow of an incompressible electrically conducting viscous fluid flowing towards a wedge [Fig.1], where ![]() is measured along the surface of the wedge and
is measured along the surface of the wedge and ![]() is normal to it. The unsteadiness in the flow field is introduced by the free stream velocity
is normal to it. The unsteadiness in the flow field is introduced by the free stream velocity ![]() . A transverse magnetic filed
. A transverse magnetic filed ![]() is applied in the direction normal to the wedge surface and, it is assumed that the magnetic Reynolds number is small, so that the induced magnetic field can be neglected. Hence, the applied magnetic field contributes only to the Lorentz force which acts in the
is applied in the direction normal to the wedge surface and, it is assumed that the magnetic Reynolds number is small, so that the induced magnetic field can be neglected. Hence, the applied magnetic field contributes only to the Lorentz force which acts in the ![]() - direction. No electric field is assumed to exist and the Hall effect is negligible. The fluid properties are assumed to be constant.
- direction. No electric field is assumed to exist and the Hall effect is negligible. The fluid properties are assumed to be constant.
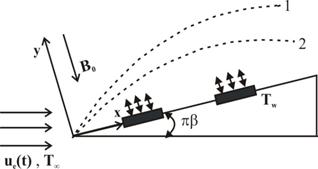
Fig. 1. Physical model and co-ordinate system.
The surface of the heated wedge is maintained at a constant temperature ![]()
![]() except at certain portions of the wedge
except at certain portions of the wedge ![]() where it varies slowly with the streamwise distance
where it varies slowly with the streamwise distance![]() .
.
Under the aforesaid assumptions and neglecting the viscous dissipation, the non-linear boundary layer equations governing the unsteady, MHD forced convection flow past a wedge are
Equation of Continuity:
![]() (1)
(1)
Equation of Momentum:
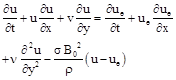 (2)
(2)
Equation of Energy:
![]() (3)
(3)
The boundary conditions to be satisfied by the above equations are:
![]()
![]()
![]()
![]()
Where
![]() ;
; ![]() (4)
(4)
Here ![]() and
and ![]() are respectively, velocity components in
are respectively, velocity components in ![]() and
and ![]() -directions of the flow;
-directions of the flow; ![]() is the inviscid flow velocity at the edge of the boundary layer ;
is the inviscid flow velocity at the edge of the boundary layer ; ![]() is the thermal diffusivity of the fluid; T is the temperature in the vicinity of the wedge; T0 is the constant temperature; t and t* are dimensional and dimensionless time;
is the thermal diffusivity of the fluid; T is the temperature in the vicinity of the wedge; T0 is the constant temperature; t and t* are dimensional and dimensionless time;![]() , are respectively, electrical conductivity, density and kinematic viscosity; L is characteristic length;
, are respectively, electrical conductivity, density and kinematic viscosity; L is characteristic length; ![]() is the Falkner-Skan power-law parameter; The subscripts
is the Falkner-Skan power-law parameter; The subscripts ![]() and
and ![]() denote conditions at the wall and in the free stream respectively;
denote conditions at the wall and in the free stream respectively; ![]() is a dimensionless constant and,
is a dimensionless constant and, ![]() or < 0, according to whether the wall is being heated or cooled. For
or < 0, according to whether the wall is being heated or cooled. For![]() , the entire wall is maintained at constant temperature
, the entire wall is maintained at constant temperature![]()
![]() . Also, when
. Also, when ![]() value is zero, the problem reduces to steady case. For the nonzero value of
value is zero, the problem reduces to steady case. For the nonzero value of![]() , the flow is accelerating if
, the flow is accelerating if![]() , provided
, provided ![]() and, the flow is decelerating if
and, the flow is decelerating if![]() .Assuming the value zero to
.Assuming the value zero to![]() , the problem reduces to the steady case. It is appropriate to point out here that numerical results pertaining to decelerating flow are obtained and discussed in this paper, since results of accelerating flow are already been published in a reputed journal.
, the problem reduces to the steady case. It is appropriate to point out here that numerical results pertaining to decelerating flow are obtained and discussed in this paper, since results of accelerating flow are already been published in a reputed journal.
Introducing the following transformations:
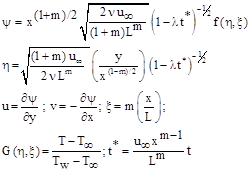 (5)
(5)
to Eqns.(1)-(3), we see that continuity equation (1) is identically satisfied and Eqns.(2) and (3) reduce, respectively, to:
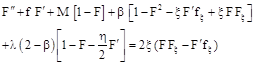 (6)
(6)
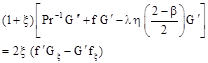 (7)
(7)
where
![]() ;
; ![]() ;
;
![]()
![]()
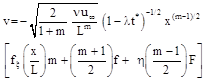
![]()
![]() ;
; ![]() (8)
(8)
The transformed boundary conditions are:
![]() for
for![]()
![]()
for ![]() (9)
(9)
Here, ![]() and
and![]() are dimensional and dimensionless stream functions respectively; F and G are the dimensionless velocity and temperature;
are dimensional and dimensionless stream functions respectively; F and G are the dimensionless velocity and temperature; ![]() is dimensionless magnetic parameter;
is dimensionless magnetic parameter; ![]() is the local Reynolds number,
is the local Reynolds number, ![]() is the Prandtl number;
is the Prandtl number; ![]() and
and ![]() are the transformed coordinates;
are the transformed coordinates;![]() is the pressure gradient parameter. Here prime ( ' ) denotes derivate with respect to
is the pressure gradient parameter. Here prime ( ' ) denotes derivate with respect to ![]() while, subscript
while, subscript ![]() represents partial derivatives with respect to
represents partial derivatives with respect to ![]() . We also note that in Eqn.(5), the parameter
. We also note that in Eqn.(5), the parameter ![]() is connected with the apex angle
is connected with the apex angle ![]() by the relation
by the relation ![]() . It is noted that the dimensionless wall temperature G (
. It is noted that the dimensionless wall temperature G (![]() ,0) given in the boundary condition (9) is a continuous function of the dimensionless streamwise distance
,0) given in the boundary condition (9) is a continuous function of the dimensionless streamwise distance ![]() with a small change in the interval
with a small change in the interval ![]() over the constant value 1. The increase or reduction in the wall temperature in the interval by the constant value introduces a finite discontinuity at the leading and trailing edges of the slot and this causes difficulties in the solution of the equation. In order to avoid these difficulties in obtaining stable numerical solutions, a non-uniform distribution of wall temperature in the interval
over the constant value 1. The increase or reduction in the wall temperature in the interval by the constant value introduces a finite discontinuity at the leading and trailing edges of the slot and this causes difficulties in the solution of the equation. In order to avoid these difficulties in obtaining stable numerical solutions, a non-uniform distribution of wall temperature in the interval ![]() has been taken, which varies slowly with
has been taken, which varies slowly with![]() and is continuous in the slot
and is continuous in the slot![]() .
.
The quantities of engineering interest are the local skin friction and heat transfer coefficient in the form of Nusselt number, and these are expressed, respectively, as:
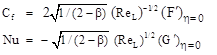 (10)
(10)
It is worth mentioning here that when![]() , the Eqns. (6) and (7) become
, the Eqns. (6) and (7) become
![]() (11)
(11)
![]() (12)
(12)
which have been considered recently by Poornima and Eswara [17], representing the steady counterpart ![]() of the present investigation.
of the present investigation.
3. Results and Discussion
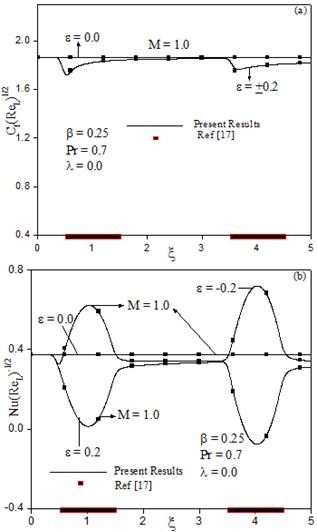
Fig. 2. Comparison of (a) skin friction coefficient and (b) heat transfer coefficient when ![]() and
and ![]() with those of Poornima and Eswara [17].
with those of Poornima and Eswara [17].
The system of non-linear partial differential equations (6) and (7) along with the boundary conditions (9) has been solved numerically employing an implicit finite difference scheme along with quasilinearization technique [19]. It may be noted that for computation purpose, two slots have been located at the intervals [0.5, 1.5] and [3.5, 4.5] and the surface is heated or cooled in these intervals only. In the remaining portion of the wedge surface, the surface is non-permeable and is maintained at constant temperature![]()
![]() . In fact, analysis has been carried out for the wedge angle 45o i.e.
. In fact, analysis has been carried out for the wedge angle 45o i.e.![]() , as the Falkner-Skan one-parameter family of solutions of the boundary layer equations has proved to be very useful in the interpretation of fluid flows at large Reynolds number. The results are illustrated graphically and are presented in Figs. 3-6.
, as the Falkner-Skan one-parameter family of solutions of the boundary layer equations has proved to be very useful in the interpretation of fluid flows at large Reynolds number. The results are illustrated graphically and are presented in Figs. 3-6.
In order to assess the accuracy of our numerical method used, we have compared the steady state results with those of White [20] [See Table 1], and Poornima and Eswara [17] [See Fig.2]. The results are found to be in excellent agreement.
Table 1. Comparison of numerical results for the case of ![]() when
when ![]()
![]() ,
, ![]() , and
, and ![]() with White[20].
with White[20].
|
|
| |||
| Present | White[20] | Present | White[20] | |
| 0.0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 0.2 | 0.0094 | 0.00939 | 0.0940 | 0.09391 |
| 0.4 | 0.0376 | 0.03755 | 0.1876 | 0.18761 |
| 0.6 | 0.0846 | 0.08439 | 0.2806 | 0.28058 |
| 0.8 | 0.1500 | 0.14967 | 0.3720 | 0.37196 |
| 1.0 | 0.2335 | 0.23299 | 0.4606 | 0.46063 |
| 2.0 | 0.8882 | 0.88680 | 0.8170 | 0.81669 |
| 3.0 | 1.7978 | 1.79557 | 0.9690 | 0.96905 |
| 4.0 | 2.7864 | 2.78388 | 0.9978 | 0.99777 |
| 5.0 | 3.7833 | 3.78323 | 1.0000 | 0.99994 |
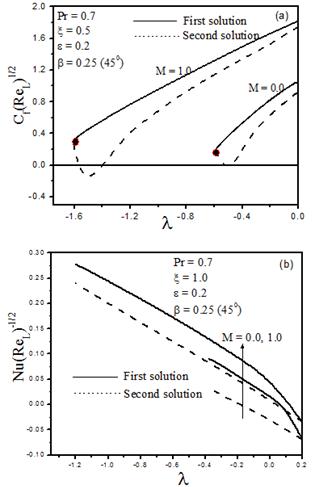
Fig. 3. The effect of magnetic field on (a) skin friction coefficient and (b) heat transfer coefficient in the presence of wall heating (![]() = 0.2).
= 0.2).
Fig. 3, shows the effect of increase in the magnetic field on skin friction and heat transfer coefficients for ![]() (wall heating),
(wall heating), ![]() (450),
(450), ![]() and
and ![]() . It is clear that, as M increases both
. It is clear that, as M increases both ![]() and
and ![]() increases. Meanwhile, the existence of the dual solution for the localized wall heating (
increases. Meanwhile, the existence of the dual solution for the localized wall heating (![]() = 0.2) are noticed for
= 0.2) are noticed for![]()
![]()
![]()
![]() 0 where
0 where ![]() is a critical value of
is a critical value of ![]() Indeed, dual solutions exist up to a critical value
Indeed, dual solutions exist up to a critical value ![]()
![]()
![]() , beyond which the boundary layer separates from the wedge surface and the solution based upon the boundary layer approximations are not possible. Moreover, the critical values of
, beyond which the boundary layer separates from the wedge surface and the solution based upon the boundary layer approximations are not possible. Moreover, the critical values of ![]() for
for ![]() are
are ![]() and for
and for ![]()
![]() when M increases from 0.0 to 1.0. It is significant to observe the role of magnetic field in the process of stabilization of the boundary layer decelerating flow during this short time. Similar trend is obtained for localized wall cooling (
when M increases from 0.0 to 1.0. It is significant to observe the role of magnetic field in the process of stabilization of the boundary layer decelerating flow during this short time. Similar trend is obtained for localized wall cooling (![]() = -0.2) and it is not presented here for the sake of brevity.
= -0.2) and it is not presented here for the sake of brevity.
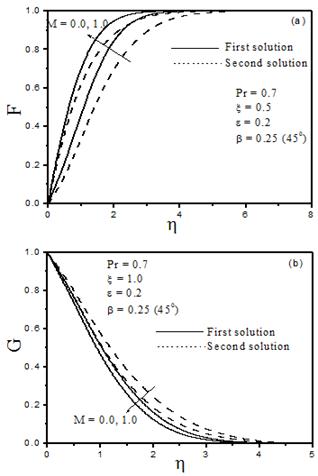
Fig. 4. The effect of magnetic field on (a) velocity and (b) temperature profiles in the presence of wall heating (![]() = 0.2) /cooling (
= 0.2) /cooling (![]() = -0.2).
= -0.2).
The variation of the velocity profile (F) and temperature profile (G) with the effect of magnetic field are plotted in Fig.4. These profiles satisfy the far field boundary conditions asymptotically, which support the obtained numerical results. In fact, the laminar boundary layer is thicker for the second solution in comparison with that of the first solution in both of these velocity and thermal profiles. It is remarked that the upper branch solutions (first solution) are stable and physically realistic, while the lower branch solutions (second solution) are not. Although such (second) solutions are not physically plausible, they are nevertheless of mathematical curiosity [14].
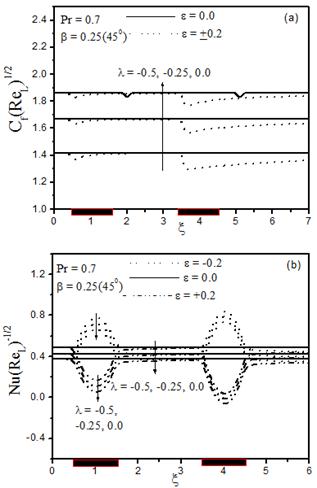
Fig. 5. The effect of unsteadiness and wall heating (![]() = 0.2) /cooling (
= 0.2) /cooling (![]() = -0.2) on (a) skin friction coefficient and (b) heat transfer coefficient.
= -0.2) on (a) skin friction coefficient and (b) heat transfer coefficient.
The variation of the skin friction [![]() ] and heat transfer [
] and heat transfer [![]() ] coefficients with the unsteady parameter
] coefficients with the unsteady parameter ![]() (decelerating flow) together with their velocity and temperature profiles are shown in Fig. 5 and 6 for
(decelerating flow) together with their velocity and temperature profiles are shown in Fig. 5 and 6 for ![]()
![]() ,
,![]() respectively. It is clear from Fig.4 that, as
respectively. It is clear from Fig.4 that, as![]() increases,
increases, ![]() increases [Fig. 5(a)] and
increases [Fig. 5(a)] and ![]() decreases [Fig.5 (b)] whenever there is localized wall heating/cooling or not. It is evident from these figures that velocity increases [Fig. 6(a)] and temperature decreases [Fig. 6(b)] at any point of the region inside laminar boundary layer, with the increase of the unsteady decelerating parameter
decreases [Fig.5 (b)] whenever there is localized wall heating/cooling or not. It is evident from these figures that velocity increases [Fig. 6(a)] and temperature decreases [Fig. 6(b)] at any point of the region inside laminar boundary layer, with the increase of the unsteady decelerating parameter![]() .
.
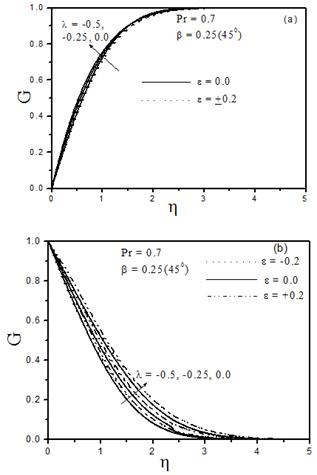
Fig. 6. The effect of unsteady parameter and wall heating (![]() = 0.2) and cooling (
= 0.2) and cooling (![]() = -0.2) on (a) velocity and (b) temperature profiles.
= -0.2) on (a) velocity and (b) temperature profiles.
4. Conclusions
In this paper, the problem of unsteady MHD forced convection decelerating flow over a wedge by considering the effect of localized wall heating /cooling has been studied. Semi-similar equations are obtained and solved by using the finite difference method along with quasilinearization technique. The analysis reveals that dual solutions are obtained for the decelerating flow in the presence of localized wall heating/cooling. Further it is found that the application of magnetic field stabilizes the laminar boundary layer flow and consequently delays the boundary layer separation.
Acknowledgment
The authors are thankful to PETRF and the Department of Mathematics, P.E.S. College of Engineering, Mandya - 571 401, for providing fabulous facilities for research work.
References
- V.M.Falkner and S.W.Skan, Some approximate solutions of the boundary layer equations, Philos.Mag.12 (1931) 865-896.
- D.R.Hartree, On an equation occurring in Falkner and Skan’s approximate treatment of the equations of the boundary layer, Proc.Cambridge Philos.Soc.33 (1937) 223-239.
- K.Stewartson, Further solutions the Falkner-Skan equation, Proc. Cambridge Phil. Soc., 50 (1954) 454-465.
- T.Watanabe, Thermal boundary layer over a wedge with uniform suction and injection in forced flow, Acta Mechanica, 83 (1990) 119-126.
- R. Kandasamy, K. Periasamy, K.K. Sivagnana Prabhu, Effects of chemicalreaction, heat and mass transfer along a wedge with heat source andconcentration in the presence of suction or injection, Intl. J. Heat Mass Trans.48 (2005) 1388–1394.
- A. Pantokratoras, The Falkner–Skan flow with constant wall temperature and variable viscosity, Intl. J. Therm. Sci. 45 (2006) 378–389.
- A.T. Eswara, A parametric differentiated finite-difference study of Falkner-Skan problem, Bull. Cal. Math. Soc. 90 (1998) 191-196.
- A.Asaithambi, A finite-difference method for the Falkner-Skan equation, Appl. Math.Comp. 92 (1998) 135-141.
- M. J. Martin and I. D. Boyd, Falkner-Skan flow over a wedge with slip boundary conditions, Journal of Thermophysics and Heat Transfer, 24 No.2 (2010) 263-270.
- S.D.Harris, D.B. Ingham and I. Pop, Impulsive Falkner-Skan flow with constant wall heat flux: revisited, International Journal of Numerical Methods for Heat and Fluid Flow, 19 (2009) 1008-1037.
- N.G.Kafoussias and N.D.Nanousis, Magnetohydrodynamic laminar boundary layer flow over a wedge with suction or injection, Canadian Journal of Physics, 75 (1997) 733-745.
- S.P.A. Devi, R. Kandasamy, Thermal stratification effects on non linear MHD laminar boundary-layer flow over a wedge with suction or injection, Intl. Commun. Heat Mass Trans. 30 (5) (2003) 717–725.
- T.Cebeci and P.Bradshaw, Physical and computational aspects of convective heat transfer, Springer, New York, 1984.
- H.Schlichting and K.Gersten, Boundary Layer Theory, Eight revised and enlarged ed., Springer-Verlag, Berlin, 2000.
- A.J.Chamkha, H.S.Takhar and G.Nath, Mixed convection flow over a vertical plate with localized heating(cooling), magnetic field and suction (injection), Heat Mass Transfer, 40(11) (2004) 835-841.
- M.Kumari and G.Nath, Mixed convection boundary layer flow over a thin vertical cylinder with localized injection/suction and cooling/heating, International Journal of Heat and Mass Transfer, 47 (2004) 969-976.
- C. Poornima and A.T. Eswara, Non-similar MHD Falkner-Skan flow with localized wall heating (cooling),Proceeding of 23rd International Congress of Theoretical and Applied Mechanics, (ICTAM-2012), Beijing (2012)
- C. Poornima and A.T. Eswara, Unsteady MHD forced flow over a wedge with localized wall heating (cooling) and suction(injection),International J. of Pure & Engg. Mathematics, Vol. 3 No. I (April 2015), pp. 1-16.
- K. Inouye and A. Tate, Finite difference version of quasilinearization applied to boundary layer equations, A.I.A.A.J. 12 (1974) 558-560.
- F. M. White, Viscous Fluid Flow, 3rd Edition. Mc. Graw-Hill, New York, 2006.



