Unsteady MHD Decelerating Flow over a Wedge with Heat Generation/Absorption
G. Ashwini1, *, A. T. Eswara2
1Department of Mathematics, Govt. College for Women’s, Mandya, India
2Department of Mathematics, GSSS Institute of Engineering and Technology for Women, Mysore, India
Abstract
This paper deals with the study of unsteady, MHD laminar boundary layer forced flow of an incompressible electrically conducting fluid over a wedge in the presence of heat generation/absorption. Similarity transformation is used to convert the governing nonlinear boundary-layer equations to non-linear ordinary differential equations and later, these equations are solved numerically using Keller-box method to obtain self-similar solutions. The results are obtained for local skin friction coefficient and Nusselt number for different governing flow parameters. It is found that dual solutions exist up to a critical value of the unsteady parameter beyond which, the boundary layer separates from the surface. Further, it is established that application of the magnetic field delays the boundary layer separation.
Keywords
MHD Decelerating Flow, Self-Similar Solution, Skin Friction, Heat Transfer, Heat Generation/Absorption
Received: July 4, 2015
Accepted: July 20, 2015
Published online: July 31, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
In their innovative work of 1931, Falkner and Skan [1] have explored two-dimensional incompressible flow past a wedge. Since then it has been studied by many researchers [2-14] employing various methods suitable for flow and heat transfer phenomena.
The hydro-magnetic boundary-layer flow and heat transfer in a incompressible electrically conducting fluid over a wedge is a significant type of flow having wide applications in industries and engineering. This type of flow has attracted the interest of many researchers due to its applications in MHD generators, plasma studies, nuclear reactors, geothermal energy extractions. Indeed, Vajravelu and Nayfeh [15] examined the hydromagnetic convection at a cone and a wedge. Kafoussias and Nanousis [16] have considered the magneto hydrodynamic Falkner-Skan flow with suction or injection. K.A.Yih [17] studied MHD forced convection flow adjacent to a nonisothermal wedge while, Seddeek. et al. [18] presented similarity solutions for a steady MHD Falkner-Skan flow and heat transfer over a wedge.
Of late, Ashwini and Eswara [19] have presented the effect of internal heat generation or absorption on the Falkner-Skan boundary layer flow with an applied magnetic field.
In all the above studies the effect of unsteadiness were not studied. Hence, the present study is aimed at analyzing the unsteady, MHD decelerating self-similar Falkner-Skan flow with internal heat generation or absorption where unsteadiness in the flow is due to the time-dependent free stream velocity. The governing non-linear partial differential equations are reduced to a system of non-linear ordinary differential equations by applying similarity transformations. Later, they are solved numerically using an implicit finite difference scheme viz., Keller-box method, to obtain self-similar solutions. Similarity solutions are very useful in the sense that they reduce the independent variables of the problem.
It is remarked here that the counter part of the present paper pertaining to accelerating flow has been studied recently by Ashwini and Eswara [20].
2. Mathematical Formulation
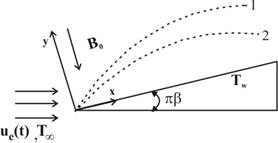
Fig. 1. Physical model and co-ordinate system for unsteady MHD Falkner- Skan wedge flow, where 1 and 2 represent edge of thermal and momentum boundary layers, respectively.
Consider the flow of an unsteady laminar incompressible viscous fluid over a wedge (Figure 1) where ![]() is measured along the surface of the wedge and
is measured along the surface of the wedge and ![]() is normal to it. The unsteadiness in the flow field is introduced by the free stream velocity
is normal to it. The unsteadiness in the flow field is introduced by the free stream velocity![]() , varying inversely with time. The temperature
, varying inversely with time. The temperature ![]() of the wall is constant and greater than that of free stream temperature
of the wall is constant and greater than that of free stream temperature![]() . A transverse magnetic field
. A transverse magnetic field ![]() is applied in the direction normal to the wedge surface and, it is assumed that the magnetic Reynolds number is small, so that the induced magnetic field can be neglected. No electric field is assumed to exist and Hall effect is negligible. The fluid properties are assumed to be constant and the viscous dissipation has been neglected in the energy equation. Under the above assumptions, the boundary layer equations governing the unsteady, MHD forced convection flow past a wedge is given by:
is applied in the direction normal to the wedge surface and, it is assumed that the magnetic Reynolds number is small, so that the induced magnetic field can be neglected. No electric field is assumed to exist and Hall effect is negligible. The fluid properties are assumed to be constant and the viscous dissipation has been neglected in the energy equation. Under the above assumptions, the boundary layer equations governing the unsteady, MHD forced convection flow past a wedge is given by:
![]() (1)
(1)
 (2)
(2)
![]() (3)
(3)
The boundary conditions are given by
at ![]()
as![]()
at
![]() (4)
(4)
Equations (1)-(3) are a system of partial differential equations with three independent variables ![]() and
and![]() . It is possible that these partial differential equations can be reduced to a system of ordinary differential equations, if the free stream velocity varies inversely as a linear function of time viz.,
. It is possible that these partial differential equations can be reduced to a system of ordinary differential equations, if the free stream velocity varies inversely as a linear function of time viz., ![]() where
where ![]() is the parameter characterizing unsteadiness in the free stream and
is the parameter characterizing unsteadiness in the free stream and ![]() is the non dimensional time variable (Eswara and Nath [21]; Schlichting [22]). This similarity property permits a decrease in the number of independent variables from three to one and yields treatment using ordinary differential equations instead of partial differential equations, to obtain self similar solutions for the nonzero values of
is the non dimensional time variable (Eswara and Nath [21]; Schlichting [22]). This similarity property permits a decrease in the number of independent variables from three to one and yields treatment using ordinary differential equations instead of partial differential equations, to obtain self similar solutions for the nonzero values of![]() . In fact, the flow is accelerating if
. In fact, the flow is accelerating if ![]() and the flow is decelerating if
and the flow is decelerating if![]() . In this paper results pertaining to decelerating flow are displayed and discussed, since results of accelerating flow are already been published in a standard journal. Assuming the value zero to
. In this paper results pertaining to decelerating flow are displayed and discussed, since results of accelerating flow are already been published in a standard journal. Assuming the value zero to![]() , the problem reduces to the steady case.
, the problem reduces to the steady case.
Introducing the following transformations:
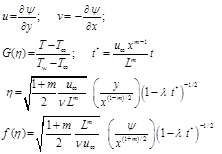 (5)
(5)
to Eqns. (1), (2) and (3), we see that the continuity Eqn. (1) is identically satisfied and Eqns.(2) and (3) reduce, respectively, to
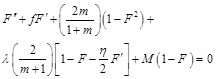 (6)
(6)
![]() (7)
(7)
where
![]() ;
; ![]()
![]()
![]() ;
;
![]()
![]() (8)
(8)
Further, we note that in (6) and (7), the parameter ![]() is connected with the apex angle
is connected with the apex angle ![]() by the relation
by the relation![]()
![]() .
.
The transformed boundary conditions are
![]() (9)
(9)
The heat generation or absorption parameter ![]() appearing in Eqn. (7) is the non-dimensional parameter based on the amount of heat generated or absorbed per unit volume given by
appearing in Eqn. (7) is the non-dimensional parameter based on the amount of heat generated or absorbed per unit volume given by ![]() with
with ![]() being constant coefficient that may take either positive or negative values. The source term represents the heat generation that is distributed everywhere when
being constant coefficient that may take either positive or negative values. The source term represents the heat generation that is distributed everywhere when ![]() is positive (
is positive (![]() ) and the heat absorption when
) and the heat absorption when ![]() is negative (
is negative (![]() );
); ![]() is zero, in case no heat generation or absorption.
is zero, in case no heat generation or absorption.
It is worth mentioning here that when![]() , Eqns. (6) and (7) reduce to:
, Eqns. (6) and (7) reduce to:
![]() (10)
(10)
![]() (11)
(11)
Which have been considered by Ashwini and Eswara [19] representing the steady counter part of the current problem. Further, Eqns. (10) and (11) reduce to those of Watanabe [6], when![]() .
.
The physical quantities of engineering interest here are the skin friction coefficient ![]() and heat transfer coefficient in the form of Nusselt number
and heat transfer coefficient in the form of Nusselt number![]() ; and they are defined, respectively, as
; and they are defined, respectively, as
![]() ,
, ![]() (12)
(12)
where
![]() and
and ![]() are shear stress and heat flux along the surface of the wedge, where
are shear stress and heat flux along the surface of the wedge, where![]() and
and![]() are dynamic viscosity and thermal conductivity, respectively. Using Eqns. (5) and (8) in (12) the skin friction and Nusselt number can be written as
are dynamic viscosity and thermal conductivity, respectively. Using Eqns. (5) and (8) in (12) the skin friction and Nusselt number can be written as
![]() and
and
![]() (13)
(13)
where ![]() , the local Reynolds number.
, the local Reynolds number.
3. Results and Discussion
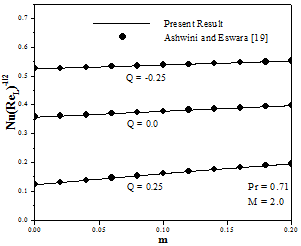
Fig. 2. Comparison of steady state (![]() ) results for
) results for ![]() when
when ![]() with those of Ashwini and Eswara [19].
with those of Ashwini and Eswara [19].
An accurate and very efficient implicit finite difference scheme called Keller-box method [23] is used to solve the coupled ordinary differential equations (6) and (7) along with boundary conditions (9). To assess the accuracy of the method which we have used, the skin friction![]() and heat transfer
and heat transfer ![]() parameter results have been compared with those of Watanabe [6] for the range of
parameter results have been compared with those of Watanabe [6] for the range of![]() ,
, ![]() [See Table I]. Further, the steady state heat transfer results for
[See Table I]. Further, the steady state heat transfer results for ![]() with a magnetic field (
with a magnetic field (![]() ) are compared with those of Ashwini and Eswara [19] [See Fig.2]. There is an excellent agreement between the present results and the above mentioned studies.
) are compared with those of Ashwini and Eswara [19] [See Fig.2]. There is an excellent agreement between the present results and the above mentioned studies.
Table 1. Comparison of steady state (![]() ) results for the range of
) results for the range of ![]() (
(![]() ) when
) when ![]() with those of Watanabe [6].
with those of Watanabe [6].



Fig. 3. Effect of magnetic field (M) on (a) skin friction and (b) heat transfer coefficients.
The effect of magnetic field![]() on skin friction [
on skin friction [![]() ] and heat transfer [
] and heat transfer [![]() ] coefficients when
] coefficients when ![]() (60o),
(60o), ![]() (no heat generation/absorption and thermal radiation) for
(no heat generation/absorption and thermal radiation) for ![]() (decelerating flow) are illustrated in Fig.3. It is observed that as magnetic field increases both
(decelerating flow) are illustrated in Fig.3. It is observed that as magnetic field increases both ![]() and
and ![]() increases quantitatively. The percentage of increase in
increases quantitatively. The percentage of increase in ![]() is about 95.65% and percentage of increase in
is about 95.65% and percentage of increase in ![]() is around 2.83% in the range
is around 2.83% in the range ![]() when
when ![]() . It is interesting to view the existence of dual solutions for both
. It is interesting to view the existence of dual solutions for both ![]() and
and ![]() , in the range of
, in the range of ![]() (
(![]()
![]()
![]()
![]() 0), and no solution for
0), and no solution for ![]()
![]()
![]() , where
, where ![]() is a critical value of
is a critical value of ![]() Therefore, solution exist up to a critical value
Therefore, solution exist up to a critical value ![]()
![]()
![]() , beyond which the boundary layer separates from the wedge surface and the solution based upon the boundary layer approximations are not possible. Based on our computation, the values of
, beyond which the boundary layer separates from the wedge surface and the solution based upon the boundary layer approximations are not possible. Based on our computation, the values of ![]() are
are ![]() and
and ![]() , respectively for
, respectively for ![]() [Fig. 3(a)] and
[Fig. 3(a)] and![]() [Fig.3(b)] in the absence of the magnetic field
[Fig.3(b)] in the absence of the magnetic field ![]() . Further, the values
. Further, the values ![]() are seen to be pushed further by the application of the magnetic field
are seen to be pushed further by the application of the magnetic field ![]() and, in fact, they are
and, in fact, they are![]() and
and ![]() , respectively for
, respectively for ![]() and
and ![]() . This vindicates the significant role played by the transverse magnetic field in the stabilization process of the laminar boundary layer flow during this short span of time.
. This vindicates the significant role played by the transverse magnetic field in the stabilization process of the laminar boundary layer flow during this short span of time.
Figure 4 shows the consequential velocity and temperature profiles of the corresponding first and second solutions, when![]() . It is clearly seen that both momentum and thermal boundary layer thicknesses are found to decrease with the increase of the magnetic field. Further, these profiles satisfy the far field boundary conditions asymptotically, which support the obtained numerical results. It is remarked that the upper branch solutions (first solution) are stable and physically realizable, while the lower branch solutions (second solution) are not. Although such solutions are deprived of physical significance, they are nevertheless of mathematical interest [22].
. It is clearly seen that both momentum and thermal boundary layer thicknesses are found to decrease with the increase of the magnetic field. Further, these profiles satisfy the far field boundary conditions asymptotically, which support the obtained numerical results. It is remarked that the upper branch solutions (first solution) are stable and physically realizable, while the lower branch solutions (second solution) are not. Although such solutions are deprived of physical significance, they are nevertheless of mathematical interest [22].

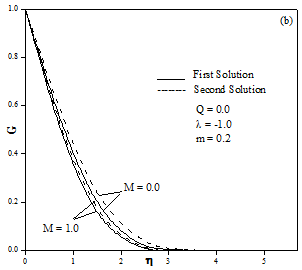
Fig. 4. Effect of magnetic field on (a) velocity (F) and (b) temperature (G) profiles.

Fig. 5. Effect of heat generation and heat absorption parameter![]() on (a) heat transfer coefficient and (b) temperature profile.
on (a) heat transfer coefficient and (b) temperature profile.
Figure 5 displays the effects of heat generation or absorption parameter (![]() ) on heat transfer coefficient [
) on heat transfer coefficient [![]() ] and temperature profiles (
] and temperature profiles (![]() ) for
) for ![]() (decelerating flow) at the wedge angle
(decelerating flow) at the wedge angle ![]() and
and ![]() . It is observed that
. It is observed that ![]() decreases as
decreases as ![]() increases (
increases (![]() ). The percentage of decrease in
). The percentage of decrease in ![]() is 23.56% at
is 23.56% at ![]() = -1.5.
= -1.5.
Fig.5 (b) shows the corresponding temperature profiles, where thermal boundary layer thickness decreases when heat is absorbed![]() , whereas opposite trend is observed for the heat generation
, whereas opposite trend is observed for the heat generation![]() . This is due to the fact that heat generation
. This is due to the fact that heat generation ![]() increases the thermal state of the fluid leading to enhancement of the heat transfer rate.
increases the thermal state of the fluid leading to enhancement of the heat transfer rate.
4. Conclusions
The effect of magnetic field and heat generation/absorption on the behavior of unsteady decelerating flow of an electrically conducting fluid flow past a wedge has been numerically investigated. Dual solutions are found to exist in forced convection decelerating flow regime. The magnetic field stabilizes the flow which in turn delays the boundary layer separation from the wedge surface. Heat generation increases thermal boundary layer thickness due to decrease in heat transfer coefficient and opposite trend is observed during heat absorption.
Acknowledgements
The authors are thankful to the reviewer for their comments and suggestions. Further, the authors express their gratitude to PETRF and the Department of Mathematics, P.E.S. College of Engineering, Mandya-571 401, for providing finest facilities for research work.
Nomenclature
|
| Free stream velocity |
|
| Wall Temperature |
|
| Free stream temperature |
|
| Transverse magnetic field |
|
| Cartesian co-ordinates along and normal to surface, respectively |
|
| Velocity components along |
|
| Thermal diffusivity |
|
| Fluid temperature |
|
| Dynamic viscosity |
|
| Kinematic viscosity |
|
| Electrical conductivity |
|
| Density of the fluid |
|
| Specific heat |
|
| Heat generation or absorption coefficient |
|
| Length of the wedge |
|
| Falkner – Skan power law Parameter |
|
| Unsteady parameter |
|
| Non-dimensional time variable |
|
| Dimensional stream functions |
|
| Dimensionless stream functions |
|
| Dimensionless velocity |
|
| Dimensionless temperature |
|
| Dimensionless magnetic parameter |
|
| Local Reynolds number |
|
| Prandtl number |
|
| Transformed coordinate |
|
| Hartree pressure gradient parameter |
Subscripts
|
| Conditions at the free stream |
|
| Conditions at the edge |
|
| Conditions at the wall |
Superscripts
| (’) | Partial derivatives with respect to η |
References
- V. M. Falkner and S. W. Skan. "Some approximate solutions of the boundary layer equations". Philos. Mag. 12(80); (1931), pp. 865-896.
- J. C. Y. Koh and J. P. Harnett. "Skin friction and heat transfer for incompressible laminar flow over a porous wedge with suction and variable wall temperature". Int. J. Heat Mass Transfer. 2 (1961), pp. 185-198.
- H. Craven and L. A. Peletier. "On the uniqueness of solutions of the Falkner-Skan equation". Mathematika. 19 (1972), pp. 135-138.
- P. Brodie and W. H. H. Banks. "Further properties of the Falkner-Skan equation". Acta Mechanica. 65 (1986), pp. 205-211.
- H. T. Lin and L. K. Lin. "Similarity solutions for laminar forced convection heat transfer from wedges to fluids of any Prandtl number". Int. J. Heat Mass Transfer. 30 (1987), pp. 1111-1118.
- T. Watanabe. "Thermal boundary layer over a wedge with uniform suction and injection in forced flow". Acta Mechanica. 83 (1990), pp. 119-126.
- A. Asaithambi. "A finite-difference method for the Falkner-Skan equation". Appl. Math. Comp. 92 (1998), pp. 135-141.
- A. T. Eswara. "A parametric differentiated finite-difference study of Falkner-Skan Problem". Bull. Cal. Math. Soc. 90 (1998), pp. 191-196.
- M. A. Hossain, M. S. Munir and D. A. S. Rees. "Flow of viscous incompressible fluid with temperature dependent viscosity and thermal conductivity past a permeable wedge with uniform surface heat flux". Intl. J. Therm. Sci. 39 (2000), pp. 635-644.
- W. T. Cheng and H.T. Lin. "Non-similarity solution and correlation of transient heat transfer in laminar boundary layer flow over a wedge". Intl. J. Eng. Sci. 40 (2002), pp. 531-548.
- S. D. Harris, D. B. Ingham and I. Pop. "Unsteady heat transfer in impulsive Falkner-Skan flows: Constant wall temperature case". Eur. J. Mech. B/Fluids. 21 (2002), pp. 447- 468.
- B. L. Kuo. "Application of the differential transformation method to the solutions of Falkner- Skan wedge flow". Acta Mechanica. 164 (2003), pp. 161-174.
- R. Kandasamy, K. Periasamy and K. K. Sivagnana Prabhu. "Effects of chemical reaction, heat and mass transfer along a wedge with heat source and concentration in the presence of suction or injection". Intl. J. Heat Mass Trans. 48 (2005), pp. 1388-1394.
- K.Bor-Lih "Heat transfer analysis for the Falkner–Skan wedge flow by the differential transformation method". Intl. J. Heat Mass Trans. 48 (2005), pp. 5036-5046.
- K. Vajravelu and J. Nayfeh " Hydromagnetic convection at a cone and a wedge". Int. Commun, Heat and Mass Transfer. 19 (1992), pp. 701-710.
- N. G. Kafoussias and N. D. Nanousis "Magnetohydrodynamic laminar boundary layer flow over a wedge with suction or injection". Canadian Journal of Physics. 75 (1997), pp. 733-745.
- K. A. Yih. "MHD forced convection flow adjacent to a nonisothermal wedge". Int. Commun. Heat Mass Transfer. 26 (1999), pp. 819-827.
- M. A. Seddeek, A. A. Afify and A. M. Al- Hanaya "Similarity Solutions for a Steady MHD Falkner - Skan flow and heat transfer over a wedge considering the effects of variable viscosity and thermal conductivity". Applications and Applied Mathematics. 4 (2); (2009), pp. 303-313.
- G. Ashwini and A. T. Eswara. "MHD Falkner-Skan boundary layer flow with internal heat generation or absorption". Int. Conf. on Mechanical, Aeronautical and Manufacturing Engg. Proc. of World Academy of Science, Engg. and Tech.,(WASET) Tokyo. Japan. 65 (2012), pp. 687-690.
- G. Ashwini, C. Poornima and A. T. Eswara. "Unsteady MHD accelerating flow past a wedge with thermal radiation and internal heat generation / absorption". Int. J. of Math. Sci. & Engg. Appls. 9(I); (2015), pp. 13-26.
- A. T. Eswara. and G. Nath. "Effect of large injection rates on unsteady mixed convection flow at a three-dimensional stagnation point". Int. Journal of Non-Linear Mechanics. 34 (1999), pp. 85-103.
- H. Schlichting and K. Gersten,: "Boundary Layer Theory". Springer-Verlag, Berlin (2000).
- H. B. Keller. "Numerical methods in boundary- layer theory". Ann. Rev. Fluid Mech. 10 (1978), pp. 417-433.



