"Restricted Euler Equations" Model Is Not Very Suitable for Revealing Properties Inherent to Euler Equations

Vladimir A. Dobrynskii^*

Institute for Metal Physics of N.A.S.U., Kiev, Ukraine

Abstract

For the restricted Euler equations, we prove the following: 1) If there is a time instant such that the perfect vector alignment between the vorticity vector and the strain matrix eigenvector happens at some point inside the 3D incompressible restricted Euler flow, it continues then permanently and keeps forever in the sense that one happens successively at all points which belong to the given point trajectory generated by the flow. 2) If the aforementioned trajectory exists, then, depending on initial data, one can either blow up for a finite time or not. What is interesting in doing so is that the aforesaid finite-time blow ups can be various and very different. In particular, we found the blow up such that the strain matrix eigenvalues all go at infinity (which can be both positive and negative) whereas the vorticity remains bounded at the same time. Such kind the vorticity behavior should be considered, generally speaking, as slightly unexpected if to take into account the well-known Beale-Kato-Majda (abbr. BKM) criterion for solutions of the genuine Euler equations to blow up at a finite-time. On the other hand, there are solutions to the restricted Euler equations which blow up at a finite time by a scenario similar to that is described in the BKM criterion. Summarizing all what is the aforesaid we see that the restricted Euler equations are not suitable enough for revealing properties inherent to the Euler equations.

Keywords

Finite-Time Blow up, the Euler Equations, the Restricted Euler Equations, Alignment, Vorticity, Strain, Vortex Stretching

Received: July 2, 2015
Accepted: August 3, 2015
Published online: August 13, 2015

@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/

1. Introduction

The problem of global unambiguous solvability for the 3D Euler equations of ideal incompressible fluid as well as that of whether the 3D incompressible Euler equations solution can develop a finite time singularity from smooth initial data remain the most challenging open problems in the ideal incompressible fluid mathematical theory. Their main difficulty consists in that a dependence of pressure in the fluid flow on its velocity is non-local. In order to overcome this difficulty, a so-called model of the "restricted Euler equations" is proposed. (For the model definition, see the following paper text.) In this model, the original pressure term of the Euler equations is changed by a certain local expression. The model idea goes back to Viellefosse [1, 2], Novikov [3] and Cantwell [4]. Later, the given model is studied in [5, 6, 7] by Liu, Tadmor and Wei. This paper prolongs exploration of the restricted Euler equations properties which was begun in [11].

2. Preliminaries

We start of the Cauchy problem for the 3D incompressible Euler equations in although results presented below all remain valid for such of the kind flows inside open both bounded and unbounded subsets of  having smooth boundary as well as for the periodic flows in a torus. So, we consider the following problem:

           (1)

where  is the material derivative,  is the gradient operator with respect to , is the given initial flow velocity satisfying  Here and in what follows 3D vectors and scalars are designated by bold letters and ordinary ones respectively. That is ,and. As a rule, we shall omit the designation on the space-time co-ordinates if those are designated by  and such the omission will not lead to misunderstanding, and, on the contrary, we shall point out such the dependence otherwise. For the given velocity  and pressure  let us introduce the  matrices

 

 

 

where  and  is the Kronecker delta symbol, i.e.  when

 and  otherwise. We recall that is related to the vorticity

 by means of the formulas  

where  is the Eddington alternating skew-symmetric tensor with the normalization . Other designations we use are following. Operations of a vector (external) product and scalar (inner) one are designated by the signs  and  respectively. Thus, for any and ,

. We shall denote the vector by .

In what follows we shall use notions of the fluid particle trajectory, the Lagrangian particle marker, the Lagrangian variable also. Let us set

, .

Definition. The function of  is said to be the fluid particle trajectory of the flow  if it is a unique solution of the following differential equation:

                (2)

where is the classical solution of Eq.(1) such that.

The pair  is called the Lagrangian variables. Here  is the Lagrangian particle marker and  is time. A totality of all the solutions of Eq.(2) generates a fluid particle trajectory mapping  Since transition from the Euler fluid flow discription to the Lagrangian one results in changing of the variable  on the variable , it is suitable  to call the Lagrangian variable also. In what follows we shall assume always that and  are considered for the maximal time interval of existence of the classic (strong) solution of Eq.(1) and shall not indicate a function dependence on the Lagrangian variables if it will not generate ambiguity and misunderstanding.

3. Main Results

Given ,we define a vorticity direction field by the formula

where .Let  For , we define then the following scalar fields   

  where by  is designated the angle between and . Notice that  is well-defined provided that

because Since we see

Lemma 1.

Proof. This formula is a corollary of that for the two-fold vector product. Indeed, according to the two-fold vector product formula

. Taking a scalar product of both the given equality sides with  we find that

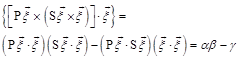
Let us derive differential equations for  and . To do this let us compute the material derivatives of  and .Keeping in mind that    and , we obtain, on one hand, that

and, on the other hand, that

Hence

                      (3)

Similarly, we find, on one hand, that

 and, on the other hand, that

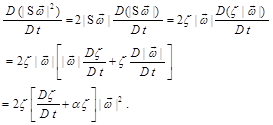
Hence

                            (4)

Substituting  instead of  in Eq. (4) and subtracting Eq.(3) from the obtained equality term-wise we get finally the following differential equation

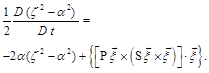            (5)

Definition. Two non-zero vectors of  and  are said to be aligned perfectly if ,i.e. when their vector (external) product is equal to zero.

Considering Eq.(5) one can easily see that  can be a solution to Eq.(5). Keeping in mind  one can easily find the differential equation for :

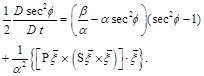         (6)

Considering Eq.(6) one can easily see that  can be solutions to Eq.(6). In particular, this is the case when and  are aligned perfectly. Indeed, by definition, the non-zero vectors  and  are aligned perfectly provided that , i.e. when .

To define a notion of the restricted Euler equations, let us compute all

partial derivatives of the first equation of Eq.(1). In doing so we obtain the following equality

                             (7)

Taking the symmetrical and antisymmetrical parts of Eq.(3) we find that

.                (8)

In general the Hessian is the non-local non-isotropic matrix. Computing

 of Eqs. (7, 8) we find that , where  is a trace of the matrix .

Definition. If to make violence and to assume  to be local and isotropic of the kind , we obtain then a model which is now called the "restricted Euler equations" [8].

Here, the elliptic pressure constraint,,is concerned solely with the diagonal elements of .

Let us study the restricted Euler equations. Since, for any  and , , is the eigenvector of .

The latter implies in turn that identically, for all  and .¹

This leads to considerable simplification of Eqs.(5,6) which take the following form:

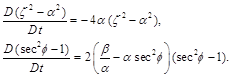      (9)

If to use the Lagrangian variable, we can then rewrite Eq. (9) legitimately as

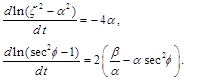          (10)

Integrating Eq. (10) we obtain two families of solutions of the kind

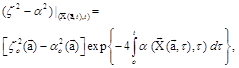           (11)

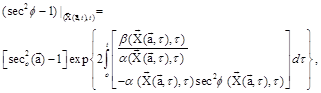
where   It is evident from Eq.(11)that for  provided  as well as

for  provided  too. Thus we proved the following.

Proposition 1. Given the restricted Euler equations. If there is  such that  are aligned perfectly, then  are aligned perfectly forever, for all admissible .

Let  be the eigenvectors of  associated with its eigenvalues  There is a generally accepted convention respecting ordering of  It is not assumed in what follows. It is not difficult to show that if  is an eigenvector for  i.e., for example, then, in the frame of  the operators of  and  take the following looks:

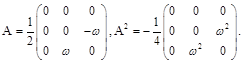
In order to prove what is just aforesaid let us find now what is a matrix form of  in the orthonormal frame of eigenvectors of  provided that  is one of the eigenvectors of .

Lemma 2. Given  be an eigenvector for  associated with its eigenvalue . Then , are the very same for .

Lemma 3. Let  be an eigenvector for or .Then  is the same for .

Proof of the lemmas. First of all notice that  Therefore, due to the definition of , if  is the eigenvector for  associated with its eigenvalue , the one is the eigenvector for  associated with the very same eigenvalue and vice versa.

Remark. Keeping in mind that the eigenvalues of  all are real we can see that if  is the eigenvector for or, then one is associated to the mutual real eigenvalue of and.

It can be easily to check that there is a rotation symmetry of solutions to the restricted Euler equations in the sense of if  is a solution pair to the restricted Euler equations, then  is the same pair for any real orthogonal matrix  (i.e. such that ). It is well-known also (see, e.g., [9], p. 258) that any real symmetric matrix is orthogonally similar to the diagonal one. Therefore, without loss of generality, we can assume that the aforementioned coordinate transformation is made from the very beginning and the Cartesian coordinates are chosen in such a manner that they coincides accurate to translation on some constant vector with the eigenvector frame of  and in doing so the vorticity direction  coincides, for instance, with that of the -axis, i.e. that It is evident that, in the given frame,is the diagonal matrix whose non-zero entries are  Keeping in mind this and that  one can specify better entries of  in such a manner:  Since  is the eigenvector for and, we find, as a corollary, that and also that  Therefore, in the frame under consideration, the matrices  should have in general the following look:

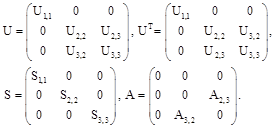
Remark. We notice attention that although the matrices and have a canonical look in the eigenvector frame of , the ones are not normal. It can be easily checked if to compute products  and to compare them then.

Applying to  methods used in [5] for studying of behavior of eigenvalues of one can show by the very same manner as it is done in [5] that, in the case  dynamics of  are described by the next equations:

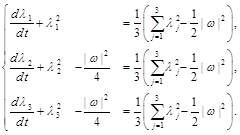        (12)

Really, keeping in mind that , we can rewrite the first equation of Eq.(8)in such a manner:

              (13)

Remark. It is worth to give attention that Eq.(12) is distinctly

distinguished from that presented in [5,7] (see, for example, Eq.(6.2)[5] or Eq.(1.6)[7]). This difference occurs because of different objects under study: we consider the strain matrix  while the authors of [5-7] examine the velocity gradient matrix .

Proposition 2. Given the restricted Euler equations. If  i.e. is the eigenvector for  associated with its eigenvalue, then the dynamics of  is governed by Eq.(12).

Proof.  by definition. Differentiating this relation with respect to $t$ we find  Computing a scalar product of the given equality terms with  we obtain . Differentiation of the same relation with respect to leads to

Multiplying this equality by  first and taking then a scalar product with  we have  Therefore,

Observing that  and that  as well as  and combining these facts with ones stated above one can easily see due to Eq.(13) that the proposition statement is valid in fact.

Subtracting the last equation of Eq.(12) from the previous one termwise we find after easy transformations that

Integrating this equation we obtain

       (14)

On the other hand, recalling that  and taking into account that  is the eigenvector for  associated with its eigenvalue  we see that . Using the Lagrangian variables converts it to the following . Integrating of the latter gives

                (15)

Comparing Eqs.(14-15) one can see that

.                       (16)

Thus, in the case under consideration, dynamics of is the very same as that of difference of the matrix  eigenvalues which are not associated with  Substituting instead of  in Eq.(16) we find that

If to substitute the expressions of and  involving and  in the first two equations of Eq.(12) only we obtain the next ones:

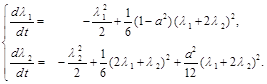  (17)

When  we can easily integrate the first equation of Eq.(17).

                              (18)

We see that  does not blow up for a finite time provided and blows up at for any . In doing so  as

. But what is interesting is  as .

Unfortunately, we can say nothing respecting whether such the behavior of  contradicts to the celebrated BKM criterion [10] or not because the latter involves norms of  in the Sobolev space  and integrals with respect to time of those of  in the  space. Let us pay attention also to that  enlarges at infinity as although the difference  remains bounded up to time . It is a corollary of  and the behavior of stated above.

Let us change a variable setting  In doing so Eq.(17) takes the look

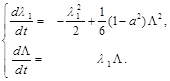                       (19)

Multiplying the former of Eq.(19) on the latter crosswise we obtain  or, otherwise,

Therefore, there is a first integral

                           (20)

where  We take into account here that  and  Solving Eq.(20) we find  

Substituting the given expression in Eq.(19) we obtain

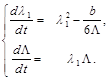                          (21)

When  we can easily integrate the first equation of Eq.(21).

Namely:  We see that  has no blow up for a finite time provided  and blows up at for any . The same takes place for  and  too.

What is the aforesaid can be summarized in view of the following.

Proposition 3. Given the restricted Euler equations. If there is

 such that  are aligned perfectly, then, for certain initial conditions, the eigenvalues of  lose their initial smoothness for a finite time by means of the so-called "finite-time blow up". As for the vorticity, it can as undergo the similar blow up at the same time as cannot.

Thus, an approach based on studying of the perfect alignment between the vorticity vector and the strain matrix eigenvectors permits us to deepen some results in [5] and to specify scenarios of the finite time blow ups of the restricted Euler equations solutions. To be more precise, Lemmas 6.1 - 6.2 [5] inform that the aforesaid solutions blow up at a finite time for almost all initial gradient matrix  But they say nothing how it occurs and what happens at the blow up time. The principal results presented above describe two concrete very different scenarios of the aforesaid blow ups.

Remark. We would like to attract a reader attention once more to that a

situation when the eigenvalues of  blow up for a finite time and in doing so the vorticity does not is, generally speaking, unexpected if to take into account the celebrated BKM criterion for solutions to the (genuine!) Euler equations to blow up at a finite time.

4. Conclusions

Summarizing all what is the aforesaid respecting the blow ups of solutions to the restricted Euler equations we can infer that their properties differ from those of solutions to the genuine Euler equations very essentially. Really, as is just marked above there are parameter data and initial conditions such that the eigenvalues of the strain matrix  for the restricted Euler equations blow up for a finite time and in doing so their vorticity does not and vice versa. However, such kind a behavior is completely not possible for the Euler equations because, as it was shown by G.Ponce in [12], a finite-time blow up of the Euler equations vorticity  accompanies the very same one of the strain matrix  and, as a corollary, of its eigenvalues and vice versa. Therefore, the model under study cannot be considered as suitable one for recognizing and study of properties inherent to the Euler equations solutions. Nevertheless, in itself it is of considerable interest because exhibits unexpected features.

References

1. Viellefosse P.: Local interaction between vorticity and shear in aperfect incompressible fluid. J. Phys. Paris. vol.43 (1982), 837-842.
2. Viellefosse P.: Internal motion of a small element of fluid in aninviscid flow. Physica A. vol.125 (1984), 150-162.
3. Novikov E.A.: Internal dynamics of flows and formation of singularities. Fluid Dynam. Res. vol.6 (1990), 79-89.
4. Cantwell B.J.: Exact solution of a restricted Euler equation for thevelocity gradient tensor. Phys. Fluids. vol.4, no. 4 (1992), 782-793.
5. Liu H. and Tadmor E.: Spectral dynamics of the velocity gradient field in restricted flows. Commun. Math. Phys. 228 (2002), 435-466.
6. Liu H. and Tadmor E.: Critical thresholds in 2D restricted Euler-Poisson equations. SIAM J. Appl. Math., vol. 63, no. 6 (2003), 1889-1910.
7. Liu H., Tadmor E. and Wei D.: Global regularity of the 4D restrictedEuler equations. Physica D (2009), doi: 10.1016/j.phesd.2009.07.009.
8. Gibbon J.D.: The three-dimensional Euler equations: Where do we stand? Physica D. vol. 237 (2008), 1894-1904.
9. Gantmakher F.R., Theory of Matrices, 3th edition, "Nauka" PublishingHouse, Moscow, 1967, 575 p. (in Russian).
10. Beale J.T., Kato T. and Majda A.: Remarks on the breakdown of smoothsolutions for 3-D Euler equtions. Commun. Math. Phys. 94 (1984), 61-66.
11. Dobrynskii V.A.: Perfect vector alignment of the vorticity and thevortex stretching is one forever. Forum Mathematicum (2011, september), DOI~10.1515~/FORM.2011.149, 13 pp.
12. Ponce G.: Remarks on a paper by J.T.Beale, T.Kato and A.Majda.Commun. Math. Phys. 98 (1985), 349-353.