An New Iterative Scheme for Variational Inequalities and Nonexpansive Mappings in Hilbert Spaces

Qiqiong Chen^{1, *}, Congjun Zhang²

¹Department of Applied Mathematics, Nanjing University of Science and Technology, Nanjing, Jiangsu, China

²College of Applied Mathematics, Nanjing University of Finance and Economics, Nanjing, Jiangsu, China

Abstract

In this paper, a new three-step iterative scheme is introduced for finding the common element of the set of fixed points of a nonexpansive mapping and the set of solutions of a variational inequality for -inverse-strongly monotone mappings. The result reveals that the proposed iterative sequence converges strongly to the common element of this two. And our studies can be regarded as an extension of the existing results, which we illustrate one by one in our remarks.

Keywords

Variational Inequality, Nonexpansive Mapping, Fixed Point

Received:May 18, 2015
Accepted: May 27, 2015
Published online: July 9, 2015

@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/

1. Introduction

Variational inequalities first studied by Stampacchia [1] in 1960s have played an important role in the development of pure and applied mathematics. They have also witnessed an explosive growth in theoretical progression, algorithmic development, etc.; see e.g. [2-14]. Let  be a real Hilbert space, whose inner product and norm are denoted by and ‖.‖, respectively. Let  be a nonempty closed convex subset of  and  a mapping from  to . The classical variational inequality problem is to find a vector  such that

,

For all or  The set of solutions of the variational inequality is denoted by . A mapping  of  to is called α-inverse-strongly monotone [6] if there exists a positive real number α such that

for any . A mapping  of  into itself is called nonexpansive [6] if

for all . We denote the set of fixed points of  by .

In order to seek for an element of  Takahashi and Toyoda [4] introduced the following iterative scheme

            (1)

for every , where  is a sequence in and  is a sequence in (0,2 is the metric projection of  onto  They proved that the iterative consequences  generated by (1) converge weakly to an element  For convenience, we will use  through the whole paper.

On the other hand, Iiduka and Takahashi [5] put forward another iterative scheme:

             (2)

for every , where  is a sequence in  is a sequence in (0, 2 is the metric projection of  onto  It was proved that the iterative consequences  generated by (2) converge strongly to an element .

Furthermore, Yao and Yao [6] proposed the following mixed gradient method:

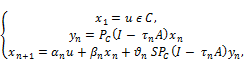        (3)

for every , where  , are sequences in  satisfied  and  is a sequence in (0, 2 is the metric projection of  onto  They proved that the iterative consequences defined by (3) converge strongly to  , where  was the metric projection of  onto

In recent years, many authors have studied some different iterative schemes both in Hilbert spaces and Banach spaces, see e.g. [2-14]. Inspired and motivated by those previous researches, we suggest and analyze a new iterative scheme for finding a common element of the set of fixed points of a nonexpansive mapping and the solution set of a variational inequality for -inverse-strongly monotone mapping in real Hilbert spaces. Strong convergence theorems are established and the iterative methods considered by [4,5,7,10] are included in our results.

2. Preliminary

For convenience, we would like to list some definitions and fundamental lemmas which are useful in the following consequent analysis. They can be found in any standard functional analysis books such as [15,16].

Definition 2.1 A mapping  is a contraction on  if there exists a constant  such that

Definition 2.2 A set-valued mapping  is called monotone if for all  and  imply

Definition 2. 3 A monotone mapping  is maximal if its graph  is not properly contained in the graph of any other monotone mapping.

It is known that a monotone mapping  is maximal if and only if, for  for every  implies  Let  be a monotone mapping of  into  and let be the normal cone operator to  defined by . Define

                  (4)

Then  is maximal monotone and  if and only if  (see [11]).

Definition 2.4 For every point , there exists a unique nearest point  in  denoted by , such that  for all  is called the metric projection of  onto

It is well known that  is a nonexpansive mapping of  onto  and satisifies for every  

Moreover,  is characterized by the following properties:

 for all             (5)

It is easy to see that the following is true:

        (6)

Note that  satisfies Opial's condition [17], i.e., for any sequence  with  the inequality

 holds for every  with

Next we present some useful lemmas.

The following lemma is an immediate consequence of equality:

Lemma 2. 1 Let  be a real Hilbert space. Then the following inequality holds:

Lemma 2. 2 (Osilike [14]) Let  be an inner space. Then for all  and  with  we have

=

Lemma 2. 3 (Xu [10]) Assume  is a sequence of nonnegative real numbers such that )+, where  is a sequence in  and  is a sequence such that

(i).   =

(ii).    or

Then

For convenience, we use  for strong convergence and  for weak convergence in the following analysis.

3. Main Results

In this section, we suggest and analyze a new iterative scheme for finding the common element of the fixed points of a nonexpansive mapping and the solution set of variational inequalities for an -inverse-strongly monotone mapping in a real Hilbert space. Strong convergence theorems are established and several special cases are also discussed.

Theorem 3. 1 Let  be a nonempty closed convex subset of a real Hilbert space  Let  be an -inverse-strongly monotone mapping of  into  and let  be a nonexpansive mapping of  into itself such that  be a contraction mapping with coefficient  Suppose  and  are given by

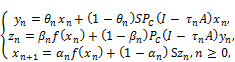           (7)

where ,{} are three sequences in  and  is a sequence in . Assume that ,{} are chosen so that  for some  with  and

(C1) =,

(C2) =,

(C3)

Then the sequence  converges strongly to  where  or equivalently  satisfies the following variational inequality:

Proof: We first show that  is a nonexpansive mapping. For all  and , we have

which implies that  is nonexpansive .

For convenience, we set

Then the iterative scheme (7) can be written as:

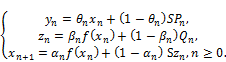             (8)

Let  Then we have  by (6) and  Since the proof of the theorem is rather long, it will be more convenient to divide the process into several steps.

Step 1. We claim that  is bounded.

Since both  and  are nonexpansive mappings, we have

   (9)

Similarly, we obtain that

                    (10)

Combining (8) and (9), together with that  is nonexpansive mapping, we see that

                   (11)

By (10) and (11), we get

Hence

     (12)

From (12), we arrive at

                (13)

By the method of induction, we have

            (14)

Therefore  is bounded. Consequently, all those sequences   are bounded.

Step 2. We now in the position to prove that

Since both  and  are nonexpansive mappings, we first have

  (15)

By similar method, we have

 (16)

In view of (15), after simple calculation, we see that

().           (17)

By (16) and (17), we get

()

+()

+                              (18)

In view of (18), we have

     (19)

Where

=[]+()

+()

+.                              (20)

By the conditions (C1), (C2) and (C3), we see that  and  which combining with Lemma 2.3, yields

.                         (21)

Since  together with (21) and the condition (C1) imply that

.                          (22)

Since  =(1-   and  is bounded, we have

.                         (23)

Furthermore, combining Lemma 2.2 with that  is nonexpansive,  is -inverse-strongly monotone mapping,  , and  we obtain that

       (24)

From (24), together with Lemma 2.2, we see that

                         (25)

which implies that

                        (26)

It follows from conditions (C1), (C2) and (21) that

                         (27)

Step 3. We show that

Since , is bounded, and we have

                        (28)

We now show that  

Since

 

= {

}

 [

],                                             (29)

we get that

+  (30)

Hence

                  (31)

It follows from (30) that

 

                                         (32)

Hence

                                       (33)

Since

  and    are bounded,

we have

                        (34)

It follows from (28), (22),(23) and (34) , together with

that

                  (35)

Step 4. We prove that

As  is bounded, there exists a subsequence  of  converges weakly to  

Since

 combining (23) and (34) we know that  

Then   

Next we show that  

Let

where  Then  is maximal monotone. Let  where  

Since  and  we have  

On the other hand, from (5) and   

we see that  Then

Thus

              (36)

Putting , we have  

Since  is maximal, we have  Hence

Now let us show that  Assume that  From Opial’s condition, we have

.                                                (37)

This is a contradiction. Thus we obtain that  

Since  is a contraction mapping, by Banach's contraction theorem, there exists a unique fixed point of , that's

Step 5. We prove that

From (5), we know

      (38)

Step 6. We claim that  From Lemma 2.1 and Lemma 2.2, we obtain that

=

.                                                                                   (39)

Then we have

.                                              (40)

That is

           (41)

where , and {}.

From (38) and conditions (C1), (C2) and (C3), letting  yields

     (42)

Let

Then + 

It is easy to check that

By Lemma 2.3, we see that

                 (43)

The proof is finished.

As an implication of Theorem 3.1, we have the following corollary:

Corollary 3.1 Let  be a nonempty closed convex subset of a real Hilbert space  Let  be an -inverse-strongly monotone mapping of  into  and let  be a be a nonexpansive mapping of  into itself such that  be a contraction mapping with coefficient k Suppose that  and  are given by

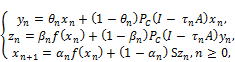
where ,{} are three sequences in  and  is a sequence in . Assume that ,{} are chosen so that  for some  with  and

(C1) =,

(C2) =,

(C3)

Then the sequence  converges strongly to  where  or equivalently  satisfies the following variational inequality:

Proof: The conclusion follows from Theorem 3.1 by setting

Theorem 3.1 extends the corresponding results of [4,5,7,10].

Remark 3.1 Putting  in Theorem 3.1, we can get the iterative scheme provided by [4].

Remark 3.2 Putting  in Theorem 3.1, we can get the iterative scheme provided by [5].

Remark 3.3 The proposition 3.1 of [7] is a special case of our result.

In fact, letting  in Theorem 3.1, we get

Then

 by Theorem 3.1.

Remark 3.4 Putting   in Theorem 3.1, we can get the iterative scheme provided by [10].

Remark 3.5 The conditions in Theorem 3.1 can be easily satisfied, for example

4. Conclusion

By introducing a new iterative scheme for variational inequalities and nonexpansive mappings in Hilbert spaces, we proved that the sequences generated by the iterative scheme strongly converge to a common element of the fixed points of a nonexpansive mapping and the solution set of variational inequality for -inverse-strongly monotone mapping.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (No. 11071109) and the China Scholarship Council (No. 201406840039). The authors are so grateful for Professor Yuanguo Zhu’s valuable suggestions to improve this paper. It is accomplished during the first author’s visit to Professor Jinlu Li at Shawnee State University, USA. The authors also would like to express their deep gratitude for the warm hospitality from Shawnee State University.

References

1. G. Stampacchia, Forms bilinearies coercitivies sur les ensembles convexes, C. R. Acad. Sci. Paris, 258 (1964) 4413-4416.
2. S. Ishikawa, Fixed points by a new iteration method, Proceedings of the American Mathematical Society, 74 (1968) 660-665.
3. A. Moudafi, Viscosity approximation methods for fixed points problems, Journal of Mathematical Analysis and Applications, 241 (2000) 46-55.
4. W. Takahashi, M. Toyoda, Weak convergence theorems for nonexpansive mappings and-inverse-strongly monotone mappings, Journal of Optimal Theory and Applications, 118 (2003) 417-428.
5. H. Iiduka, W. Takahashi, Strong convergence theorems for nonexpansive mappings andinverse strongly monotone mappings, Nonlinear Analysis TMA, 61 (2005) 341-350.
6. Y. Yao, J. Yao, On modified iterative method for nonexpansive mappings and monotone mappings, Applied Mathematical and Computation, 186 (2007) 1551-1558.
7. J. Chen, L. Zhang, T. Fan, Viscosity approximation methods for nonexpansive mapping and monotone mappings, Journal of Mathematical Analysis and Applications , 334 (2007) 1450-1461.
8. X. Qin, S. Cho, S. Kang, Convergence of an iterative algorithm for systems of variational inequalities and nonexpansive mapping with applications, Journal of Computational and Applied Mathematics, 233 (2009) 231-240.
9. S. Wang, B. Guo, New iterative scheme with nonexpansive mappings for equilibrium problems and variational inequality problems in Hilbert spaces, Journal of Computational and Applied Mathematics, 233 (2010) 2620-2630.
10. H. Xu, Viscosity approximation methods for nonexpansive mappings, Journal of Mathematical Analysis and Applications, 298 (2004) 279-291.
11. A. Bnouhachem, M. Noor, H. Zhang, Some new extragradient iterative methods for variational equilibrium problems and fixed point problems, Applied Mathematics and Comuputation, 215 (2010) 3891-3898.
12. A. Bnouhachem, M. Noor, H. Zhang, Some new extragradient iterative methods for variational inequalities, Nonlinear Analysis TMA, 70 (2009) 1321-1329.
13. T. Suzuki, Strongly convergence of Krasnoselskii and Mann's type sequences for one-parameter nonexpansive semigroupw without bochner integrals, Journal of Mathematical Analysis and Applicaations, 298 (2004) 279-291.
14. M. Osilike,D. Igbokwe, Weak and strong convergence theorems for fixed points of pseudocontractions and solutions of monotone type operator equations, Computers and Mathematics with Applicaations, 40 (2000) 559-567.
15. J. B. Conway, A Course in Functional Analysis, 2nd ed., Springer-Verlag, New York, 1990.
16. C. J. Zhang, Set-valued Analysis and Economic Applications, 2nd ed., Science press, Beijing, 2004.
17. Z. Opial, Weak convergence of successive approximations for nonexpansive mappings, Bulletin of the American Mathematical Society, 73 (1967) 591-597.