A Simulated Annealing Method to Optimize the Order of the Sequences in Continuous-Casting
Achraf Touil1, *, Abdelwahed Echchtabi1, Adil Bellabdaoui2
1University Hassan 1st, Laboratory of Mechanics, Industrial Management and Innovation, FST, Settat, Morocco
2University Mohamed V Souissi’ Information Technology Team and Corporate Management, ENSIAS, Rabat, Morocco
Abstract
The purpose of this paper is to propose a simulated annealing algorithm to maximize the production and minimize the processing time in the steelmaking continuous casting by optimizing the order of the sequences (a sequence is a group of jobs with the same chemical characteristics). Based on the work of [1] a mixed integer programming for scheduling Steelmaking-Continuous casting production with the object to minimize the makespan. The order of the sequences in continuous casting is assumed fixed. Our contribution is to analyze and suggest an additional way to determine the optimal order. A simulated annealing algorithm restricted by a tabu list (SATL) is addressed to obtain the optimal order. After parameter tuning of the algorithm, the proposed algorithm was implemented to different instances using a .NET application and the commercial software solver Cplex v12.5.
Keywords
Steel-Making, Continous-Casting, Metaheuristics, Simulated Annealing, Tabu List
Received:May 15, 2015
Accepted: June 15, 2015
Published online: July 15, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
The steel industry is an important activity that contributes to the economy development of many countries. Companies have consistently sought innovative solutions in the production process to meet multiple challenges such as competition and fluctuations in energy costs. The production scheduling is an essential tool to improve productivity through saving energy, minimizing treatment times as well as production costs.
The problems that impede planning and scheduling of steelmaking processes have been widely discussed in the literature. These problems can be classified according to the structure of the workshop (converters number, number of refining stands and number of continuous casting), constraints taken into account as well as the optimization tools used in this field namely operating research methods and artificial intelligence methods. Thus, several works are proposed based on heuristics, exact models, and expert systems, methods of constraint satisfaction, meta-heuristics, methods of human-machine coordination and multi-agent methods. [2, 3] have applied a heuristics to solve SCC. [1, 4] mathematical programming modelling approach was utilized to schedule the SCC production planning. In [5] both the concept of ant colony optimization and nonlinear optimization methods were introduced in order to solve the problem. A bee colony-based algorithm was proposed in [6] to solve the CV–RS–CC steelmaking planning and scheduling problem. To solve the SCC scheduling problem the work discussed in [7] developed a constraint programming model.
Based on the work introduced in [1] which supposes that the order of the sequences is assumed fixed, the main contribution of this work is to apply a metaheuristic algorithm to obtain the optimal order which will maximize the production and also minimize the processing time in the steelmaking continuous casting. The rest of this paper is organized as follows: section 2 introduces the mathematical model of production scheduling; section 3 presents the proposed algorithm to optimize the order of the sequences in continuous casting; section 4 deals with the numerical results; then, a summary and conclusion are given in section 5.
2. SCC Production Process Description and the Mathematical Model
In this section, the overall assumptions of this problem are defined following a description of the SCC production process.
2.1. Process Description
The steelmaking process, known in the literature as SCC (Steelmaking-Continuous-Casting), consists of three major steps (stages): (1) two identical converters (CV) (the basic oxygen furnace) with the same processing time, (2) two refining stands (RS) with the same processing time at each machine, and (3) two continuous casting (CC) with a different processing time at each charge. Different material-handling and travelling crane are considered, but we just hold back the transfer time between successive stages Fig. 1.
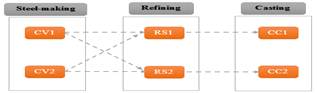
Figure 1. Schema of the layout.
The converter refines pig iron to produce the crude steel which is burnt by blowing in pure oxygen. The refining stand eliminates impurities and adjusts the chemical composition of the steel. Finally, the liquid steel is continuously poured into a bottomless mould. Guided by a set of rollers and continues cooling and solidifying, the moulded metal descends (Arcelor, 2004).
2.2. Mathematical Model
The mathematical model in [1] is based on mixed integer linear programming which concerns the scheduling of several sequences (a sequence consists of multiple jobs with the same characteristics that are treated in a given order). A sequence is dedicated to one of the two production lines (RS-CC). It is part of an already ordered set on each of the continuous casting. The objective of this scheduling is to basically maximize the production and minimize the processing time. Doing so, it should ensure the two following points:
• The jobs of the two sequences should be assigned to converters.
• Scheduling the execution of the jobs in the three steps of the steel by respecting the constraints. This involves the start of processing sequences in continuous casting (possible delays are relative to the date availability of those). And it determines the load processing time on continuous casting (possible slowdown is relative to minimum duration of treatment).
3. Literature Review
The steel production process is considered as a hybrid flow shop problem, because all jobs (tasks) visit the three steps in the same direction and at every stage there are several parallel and/or identical machines. However, it is different from classical HFS in terms of the processing jobs in the last step. Processing at this stage requires a consecutive treatment of a set of charges (sequences) on the same refining stand and in the same continuous casting. In other words, algorithms applied to HFS can solve this problem. In this paper metaheuristics is used to find a solution to this problem. The following table shows some references.
Table 1. The summary of the literatures concerning the simulated annealing applied to flow shop hybrid.
| Authors | Algorithm | Comment |
| Nearchou, 2004 | SA-GA | Approach that combines the characteristics of a canonical procedure simulated annealing with borrowed characteristics of the genetic algorithm. |
| Law et al. 2004 | MSAA | Records the characteristics of good solution and introduced into the simulated annealing to make the search process more robust |
| Ruiz et al. 2006 | GA | Genetic algorithm with new features and four new crossover operators applied to a hybrid flow shop problem. |
| Bandyopadhyay et al. 2008 | AMOSA | Incorporates the concept of archive to provide a set of compromise solutions for the problem considered |
| Laha and Chakraborty Kumar. 2008 | NEH-SA | Uses simulated annealing in conjunction with a constructive heuristic Nawaz et al. 1983 |
| Naderi et al 2009 | HSA | A compromise between intensification and diversification to increase the competitiveness of the simulated annealing method |
| Czapinski. 2010 | PSA-GA | Parallelization between simulated annealing and genetic algorithm is presented. |
| Lin et al. 2011 | MSSA | Based on the main properties of the simulated annealing (apparent convergence, small population, efficient memory usage and easy implementation). |
| Samuel et al. 2014 | NEH-SAO | Offers a simulated annealing algorithm hybridized with the NEH algorithm for flow shop problem with a new cooling scheme. |
4. The Proposed Hybrid Algorithm
The MILP described in [1], concerns several sequences already ordered. In this section, we tend to additionally analyze the possibility to optimize the order of the consecutive sequences. It is very clear that it is unrealistic to introduce directly this approach in the MILP model. Indeed, binary variables already numerous in this model are based on the known order of jobs i and j. If this order is unknown, the extension of the MILP model will require the introduction of additional binary variables to represent this order; but this unfortunately generates nonlinearities (binary variables product). Other approaches may be considered: The enumerative algorithms such as the complete enumeration, in practice this approach is more accurate in term of the quality of the solution found. However, the major drawback of this approach is the significant execution time for large instances. Hence, there is a need to consider other methods to find a compromise between the optimality of the solution and the execution time such as metaheuristics. A method based on simulated annealing (SATL) and restricted by a tabu list is described in this section to deal with the problem.
The proposed method contains two main components (Algorithm 1): Simulated annealing and tabu list. The SA is often presented as the oldest metaheuristics method; it transposes the process of annealing applied in metallurgy to solve an optimization problem. In SA not only better solutions are accepted, but also worse neighboring solutions have a probability of being accepted. By this strategy and the cooling schema, the algorithm is capable of escaping local optimum and to explore the space of solutions as much as possible. [8–11] use simulated annealing to solve parallel machine scheduling problem. On the other hand, the tabu list is one of the key factors that determine the quality of a TS algorithm in order to avoid the search process turning back to the solutions generated in the last iterations.
The main advantage of combining these components is to use the diversification strategy of simulated annealing algorithm, and the tabu list is implemented in order to: (1) store the solutions generated in the previous generations; (2) escape the local optima. The length of tabu list is a fixed size. When the tabu list is full, the oldest element of the list is replaced by the best new solutions.
The mechanism of the research in the proposed method could be described as follows: The algorithm begins the research with an initial solution generated by the NEH algorithm after the initialization of the parameters (initial temperature, final temperature).Then, a neighboring solution is generated according to the neighbourhood structure of the problem by Algorithm 2. The solution is evaluated. If the solution that results is of a lower cost than the current solution, the move is accepted and this new solution (S) becomes the current solution (S), otherwise if the new solution is of higher cost (lesser quality solution), SA accepts it with probability ![]() with
with ![]() the current temperature and
the current temperature and![]() , Otherwise the solution is rejected. After an application of the metropolis sample criteria, the temperature is updated using the geometric cooling schema. A detailed description is given in figure 2.
, Otherwise the solution is rejected. After an application of the metropolis sample criteria, the temperature is updated using the geometric cooling schema. A detailed description is given in figure 2.
4.1. Representation of a Solution
A solution is associated to the sequences prepared by the "logistics" service within a given order depending on the demand and the quality of the steel. These sequences are divided into blocks; each block contains three sequences (the last block may hold the rest). This choice is inspired by the industrial reality since the steel does not receive all of these sequences once for all. It receives packages; each of these packages allows it to have the material to make its schedules for 2-3 days. Afterwards, the rest of the sequence comes progressively. Figure.2. shows the structure of chromosome (CC1 contains the sequences in Continuous casting 1, CC2 contains the sequences in Continuous casting 2).
Algorithm 1. The pseudo code of the SA.
| Inputs: | |
| Initial solution S, Temp-in, Temp-fin, L, Amax, Rmax. | |
| Outputs: | |
| Best Solution found S* | |
| 1 | Call NEH algorithm to improve the initial solution S |
| 2 | Best individual S* = S ; f(S*) =f (S); |
| 3 | T=Temp-in |
| 4 | while T |
| 5 | l=0 |
| 6 | while L |
| 7 | Call Algorithm 3 to generate new solution; |
| 8 |
|
| 9 | if |
| 10 |
|
| 11 | else |
| 12 | if |
| 13 |
|
| 14 | A=A+1; |
| 15 | else |
| 16 | The solution is rejected ; |
| 17 | R=R+1; |
| 18 | end if |
| 19 | end if |
| 20 | if f(S*) |
| 21 | S*= S; |
| 22 | f(S*) = f (S); |
| 23 | end if |
| 24 | l=l+1; |
| 25 | end while |
| 26 | Update (T); * Update T with geometric schema * |
| 27 | end while |
| 28 | return S* |
4.2. Generation of an Initial Solution
The choice of the initial solution influences the convergence of the algorithm. Generally, the simulated annealing starts with an initial solution, which is randomly generated. In the context of this problem, in order to increase the convergence speed of the proposed algorithm, the NEH algorithm is implemented to generate the initial solution. The NEH algorithm generates an initial sequence by allotting the jobs in a sequence based on their completion times. Jobs with higher processing times are given higher priority compared to jobs with lower processing times. The NEH algorithm ensures a better initial solution and guarantees the same initial solution each time for the proposed problem.
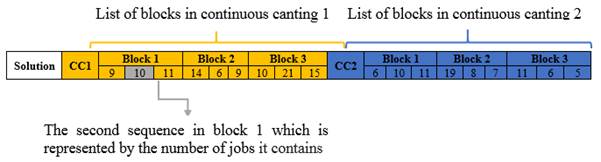
Figure 2. Solution representation.
4.3. Evaluation Function
For each solution corresponds an evaluation function corresponding to the minimization of the makespan optimization. This function is calculated by calling the commercial solver using the Cplex API.
4.4. Generation Neighbourhood Method
The generation of neighbouring solution is an essential step in the algorithm construction phases. In the present work, this generation must keep the random aspect that characterizes the simulated annealing. A detailed description is given in Algorithm 2.
Algorithm 2. Generation neighbourhood method.
| Inputs: | |
| Current solution Scurrent | |
| Outputs: | |
| New solution Snew | |
| 1 | Select randomly a continuous casting CC1 or CC2. |
| 2 | Choose randomly two blocks |
| 3 | Choose randomly a block |
| 4 | Verify the occurrence of the solution in the tabu list. If the solution has been already explored, go to step 1.Otherwise return the new solution |
4.5. New Solution Acceptation Process
At each iteration, a solution ![]() neighbor of the current solution
neighbor of the current solution ![]() is generated. Depending on its quality, the new solution
is generated. Depending on its quality, the new solution ![]() will be accepted with probability equal
will be accepted with probability equal ![]() with
with ![]() the current temperature and
the current temperature and![]() . Or will be rejected using the metropolis criterion:
. Or will be rejected using the metropolis criterion:
![]()
4.6. Cooling Schema
There is always a compromise between the quality of solutions and cooling scheme. If the temperature is slowly decreasing, the best solutions are obtained, but with a greater computation time. In our case, the temperature declines according to the following function:![]() With
With ![]() is the cooling ratio.
is the cooling ratio.
4.7. Parameter Settings
The implementation of the proposed algorithm requires the adjustment of a set of parameters that influence the process time and the objective function convergence. The SATL parameters are as follows:
i. Initial temperature (![]() )
)
The initial temperature is an essential parameter in simulated annealing. It will change the execution time of the algorithm based on the effort required to the research. In this way, T0 is chosen based on the maximum estimated difference in the objective function (Sanvicente-Sánchez et al. 2004), as follows:
![]() With
With ![]() and
and ![]() the acceptance probability of a solution to the initial temperature. In the context of this problem, it is chosen to have a solution that degrades the objective function accepted with a probability of 0.99. So, the initial temperature is
the acceptance probability of a solution to the initial temperature. In the context of this problem, it is chosen to have a solution that degrades the objective function accepted with a probability of 0.99. So, the initial temperature is![]() .
.
ii. Final temperature (![]() )
)
The final temperature is an essential parameter simulated annealing; it will stop the algorithm. The final temperature ![]() selected as if:
selected as if:
• There are no alterations in the cost value
• The probability of accepting a move is too low ![]()
The final temperature is chosen based on the minimum estimated difference in the objective function (Sanvicente-Sánchez et al. 2004), as follows:
![]() With
With ![]() and
and ![]() the acceptance probability of a solution to the initial temperature. In the context of this problem, it is chosen to have a solution that degrades the objective function accepted with a probability of 0.01. So the final temperature is
the acceptance probability of a solution to the initial temperature. In the context of this problem, it is chosen to have a solution that degrades the objective function accepted with a probability of 0.01. So the final temperature is![]()
iii. The epoch length (L)
To reach a state of equilibrium at each temperature, a sufficient number of transitions is required. The theory suggests that the number of iterations at each temperature can be exponential in the size of the problem, which is a difficult strategy to be applied in practice. The number of transitions may be as follows:
• Static: The number of transitions is determined before the start of the research. For example, it is necessary to reach the equilibrium state at each temperature.
• Adaptive: The number of neighbors generated depends on the characteristics research.
In the context of this problem, the epoch length is chosen fixed.
iv. Total neighbors to accepted (![]() )
)
Controls the number of neighbors to accept. In our case, ![]() is fixed at the beginning of the algorithm.
is fixed at the beginning of the algorithm.
v. Total neighbors rejected (![]() )
)
Controls the number of neighbors to accept. In our case, ![]() is fixed at the beginning of the algorithm.
is fixed at the beginning of the algorithm.
vi. Stopping Criterion
Concerning the stop condition, the theory suggests a final temperature equal 0. In practice, the search stops when the probability of accepting a move is negligible. In our case, the algorithm stops when one of the following conditions is fulfilled. ![]() ;
; ![]() ;
; ![]() .
.
vii. Improvement
To improve the performance of the algorithm, we added a variable that stores the best value encountered; otherwise, the algorithm may converge to a solution, then we had visited a better solution before.
5. Experimental Results
This section describes the numerical results obtained by the test of the algorithm for different instances. For this, we have developed an application in NET that allows the connection to the CPLEX solver v12.5 and the application of the SATL. The parameter tuning of the proposed algorithm are set as follows:
The initial and final temperatures: For each instance, the temperatures are determined using the equation described in the parameters section for a sample size of 20 solutions generated randomly.
The cooling ratio: is set to 0.98 for all instances.
The epoch length: 30, 40, 50.
Total number of individual to accept: 50, 100
Total number of individual to reject: 25, 30, 50.
The length of tabu list: 15, 20, 30.
Then the total number 3×2×3×3=54 of runs, 30 for the epoch length, 50 and 25 for the total number of individual to accept and reject, and 20 for length of tabu list. The numerical results found through NET application are given in table 1. The column 2 represents the size of the problem where n1 is the number of sequences in continuous casting 1 and n2 represents the number of sequences in continuous casting 2. The column 3 represents the value of the objective function of the initial order proposed by the logistics service. The column 4 shows the best results of the proposed algorithm. For the column 5, it displays the gap between the objective function value and the value obtained by the proposed algorithm.
For all instances, the algorithm obtains better solutions than the mathematical model. In order to compare the performance of the proposed algorithm, we have to measure the gap (column 5 in table 1)
![]() .
.
6. Conclusion
This paper describes an optimization problem of the order of the sequences in continuous casting. The chief objective is to find an optimal order that minimizes the processing time and maximizes the productivity. A metaheuristic algorithm based on simulated annealing restricted by a tabu list was proposed to deal with this problem. Our research findings (Results) show that the proposed algorithm SATL obtains better solutions for all instances. Using this approach, it was possible to reduce the processing time compared to the time required for the mathematical programming model. Other techniques are also applicable to evaluate the problem namely the implementation of other alternatives of the simulated annealing such as parallelization concept that increases the speed of the method and simulated annealing with multi-starts. See also approaches based on genetic algorithms.
Table 1. Results obtained with the proposed algorithm for different instances.
| Instance | Problem Size (n×m) | Initial solution (min) | SATL | Gap |
| Inst1 | 9×9 | 6415,8444 | 6298,6127 | 0,52 |
| Inst2 | 9×12 | 7528,0415 | 7410,7724 | 0,00 |
| Inst3 | 9×15 | 8314,8992 | 8281,6107 | 0,13 |
| Inst4 | 11×9 | 7129,2797 | 7099,7913 | 0,55 |
| Inst5 | 11×12 | 9374,8901 | 9321,3180 | 0,12 |
| Inst6 | 11×15 | 11924,9618 | 11802,1181 | 0,26 |
| Inst7 | 12×9 | 8406,3031 | 8316,9478 | 0,51 |
| Inst8 | 12×12 | 13021,8320 | 12915,8888 | 0,38 |
| Inst9 | 12×15 | 14510,7200 | 14490,8972 | 0,09 |
| Inst10 | 15×9 | 16327,3747 | 16280,0359 | 0,02 |
| Inst11 | 15×12 | 12405,0377 | 12399,9149 | 0,32 |
| Inst12 | 15×15 | 14134,8693 | 14127,0787 | 0,00 |
References
- Bellabdaoui et al, 2006 "A mixed-integer linear programming model for the continuous casting planning", International Journal of Production Economics, Vol.104, pp. 260-270, 2006.
- Bellabdaoui et al, 2005 "A heuristic algorithm for scheduling the steelmaking continuous casting process", in Pacific Journal of Optimization, Vol. 1, No. 3, pp. 447-464, 2005.
- Pacciarelli, D., and M. Pranzo. 2004. "Production scheduling in a Steelmaking-Continuous Casting Plant. "Computers and Chemical Engineering28: 2823–2835.
- Tang, L., J. Liu, A. Rong, and Z. Yang. 2000. "A Mathematical Programming Model for Scheduling Steelmaking-Continuous Casting Production". European Journal of Operational Research120: 423–435.
- Atighehchian, A., M. Bijari, and H. Tarkesh. 2009. "A Novel Hybrid Algorithm for Scheduling Steelmaking Continuous Casting Production. "Computers & Operations Research36: 2450–2461.
- Pan, Q.-K., L. Wang, K. Mao, J.-H. Zhao, and M. Zhang. 2013. "An Effective Artificial Bee Colony Algorithm for a Real-world Hybrid Flowshop Problem in Steelmaking Process." IEEE Transactions on Automation Science and Engineering10: 307–322.
- Xujun, Z., and L. Zhimin. 2009. "Model and Solution for the Steelmaking-Continuous Casting Scheduling Problem Based on Constraint Programming Method." In Proceedings IEEE – International Conference on Information Technology and Computer Science (ITCS 2009), 19–22, Kiev.
- Nearchou and al.2004 ‘’A novel metaheuristic approach for the flow shop scheduling problem", Engineering Applications of Artificial Intelligence, 17(3), pp 289–300.
- Naderi et al. 2009 "An improved simulated annealing for hybrid flow shops with sequence-dependent setup and transportation times to minimize total completion time and total tardiness", Expert Systems with Application, 36(6), pp 9625-9633.
- Bandyopadhyay and al. 2008 "A simulated annealing-based multi objective optimization algorithm: AMOSA", IEEE Transactions on Evolutionary.
- Czapinski, 2010 "Parallel simulated annealing with genetic enhancement for flow shop problem." Computers and Industrial Engineering, 59(4), pp 778-785.
- Nawaz, M., Enscore, E. Jr and Ham, 1983, "A heuristic algorithm for the M machine, n-job flowshop sequencing problem", Omega, Vol. 11 No. 1, pp. 91-95.



