A Meshless Method Based on Radial Basis Functions for Approximating the Oscillations Parameters of Launching Devices During the Firing
S. Sarabadan1, *, M. Kafili2
1Departeman of Mathematics, Imam Hossein University, Tehran, Iran
2Departeman of Mathematics, Amir Kabir University, Tehran, Iran
Abstract
The sloped rocket launch used in military forces is one of the most important kinds of defence instruments. The rockets stability during the firing path especially when they are unguided is very important for firing precision. It completely depends on the elementary conditions and oscillations when the firing. In this work, we consider this issue, modelling the problem results in a differential equations system of the second order. A meshless method based on radial basis functions (RBFs) is applied to solve the underlying system and the numerical results are presented in the figural forms.
Keywords
Sloped Rocket Launching Devices, Oscillations, Radial Basis Function
Received: April 9, 2015 / Accepted: April 25, 2015 / Published online: May 15, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
The study of launching device oscillations during the firing is necessary for the design of precise and efficient rocket-launching device systems, especially in the case of unguided rockets. We suppose that the launching device and the moving rocket form a complex oscillating system that join together a sum of rigid bodies bound by elastic elements (the vehicle chassis, the tilting platform and the rockets in the containers) [1]. Some authors have been considered all forces and moments to a real analysis of problem [1,2]. It results in a matrix form of the second order differential equations system that describes the matrix form of dynamic equations of the rocket-launching device system motion.
Suppose the independent unknown dynamic variables of the rocket-launching device system motion are presented in the form of the following column vector [2]:
![]() (1.1)
(1.1)
where the vehicle chassis translation ![]() , the vehicle chassis rotation
, the vehicle chassis rotation ![]() (the chassis pitch movement), the vehicle chassis rotation
(the chassis pitch movement), the vehicle chassis rotation ![]() (the chassis rolling movement), the tilting platform rotation
(the chassis rolling movement), the tilting platform rotation ![]() (the gyration movement around the vertical axes), the tilting platform rotation
(the gyration movement around the vertical axes), the tilting platform rotation ![]() (the pitch movement) and the rocket translation
(the pitch movement) and the rocket translation ![]() , are components of
, are components of ![]() . So, one can obtain the matrix form of the second order differential equations system that describes the rocket-launching system components motion:
. So, one can obtain the matrix form of the second order differential equations system that describes the rocket-launching system components motion:
![]() (1.2)
(1.2)
Where ![]() is the matrix of the velocities coefficients,
is the matrix of the velocities coefficients, ![]() ;
; ![]() is the matrix of the unknown variables coefficients
is the matrix of the unknown variables coefficients ![]() .
. ![]() is the matrix of the coefficients for the nonlinear combinations of the unknown variables:
is the matrix of the coefficients for the nonlinear combinations of the unknown variables:
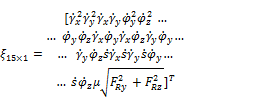 (1.3)
(1.3)
For more information about the components of matrices (1.3), that can be specified randomly, one can see [1,2]. And, the ![]() is the matrix of the external forces that acts on the system:
is the matrix of the external forces that acts on the system:
![]() (1.4)
(1.4)
The vector (1.4) is used to express the influence of the external forces on the motion system. In this vector, the first term corresponds to the weight force, the second term corresponds to the rocket thrust and the last term to the rocket jet force [2].
The mathematical model can be used to study any launching device like the underlying problem [1,2]. The rest of the paper is organized as follows: In the Section 2, a brief review on the radial basis functions (RBFs) is presented. The RBFs method is applied to the problem in Section 3. The numerical results are shown in the Section 4.
2. A Brief Review on the RBFs Method
One of the most popular meshless methods is constructed by radial kernels as basis called radial basis function (![]() ) method. It is (conditionally) positive definite, rotationally and translationally invariant. These properties make its application straightforward specially for approximation problems with high dimensions. Some of the well-known RBFs are as follows,
) method. It is (conditionally) positive definite, rotationally and translationally invariant. These properties make its application straightforward specially for approximation problems with high dimensions. Some of the well-known RBFs are as follows,
![]() (
(![]() ):
): ![]()
![]() (
(![]() ):
): ![]()
![]() (
(![]() ):
): ![]()
where![]() is the Euclidean distance between any two points
is the Euclidean distance between any two points ![]() ,
, ![]() , [3,4]. The
, [3,4]. The ![]() include two useful characteristics: a set of scattered centers
include two useful characteristics: a set of scattered centers ![]() with possibility of selecting their locations and existence of a free positive parameter,
with possibility of selecting their locations and existence of a free positive parameter, ![]() , known as the shape parameter.
, known as the shape parameter.
Assume the ![]() be the shape parameter corresponding to
be the shape parameter corresponding to ![]() center
center ![]() , we use following notation for translation of
, we use following notation for translation of ![]() at
at ![]() center,
center,
![]()
Let data values ![]() are given, the function
are given, the function ![]() will be approximated using a linear combination of translates of a single
will be approximated using a linear combination of translates of a single ![]() so that,
so that,
![]() (2.1)
(2.1)
where the unknown coefficients ![]() will be determined by collocating (2.1) at the same set of centers,
will be determined by collocating (2.1) at the same set of centers, ![]() .
.
The shape parameter plays an important role in ![]() , the choice of it controls the shape of the basis functions and interchanges the error and stability of interpolation process. This behavior is manifested as a classical trade off between accuracy and stability or Uncertainty Principle [5] which refers to the fact that an RBF approximant cannot be accurate and well-conditioned at the same time.
, the choice of it controls the shape of the basis functions and interchanges the error and stability of interpolation process. This behavior is manifested as a classical trade off between accuracy and stability or Uncertainty Principle [5] which refers to the fact that an RBF approximant cannot be accurate and well-conditioned at the same time.
Two scenarios are available for choosing shape parameters: constant shape parameter (![]() ) strategies that all of shape parameters take the same value and variable shape parameter (
) strategies that all of shape parameters take the same value and variable shape parameter (![]() ) strategies that assign different values to shape parameters corresponding to each center. Many scientists and mathematicians use
) strategies that assign different values to shape parameters corresponding to each center. Many scientists and mathematicians use ![]() in
in ![]() approximations [6,7,8] because of their simple analysis as well as solid theoretical background rather than
approximations [6,7,8] because of their simple analysis as well as solid theoretical background rather than ![]() , but there are numerous results from a large collection of applications [9,10,11,12] indicating the advantages of using
, but there are numerous results from a large collection of applications [9,10,11,12] indicating the advantages of using ![]() .
.
3. RBFs Method for Solving the Problem
At the first, one can reduce the system of second order differential equations (1.2) to a system of first order differential equations by introducing the following variables[2]:
![]() (3.1)
(3.1)
![]() (3.2)
(3.2)
![]() (3.3)
(3.3)
![]() (3.4)
(3.4)
![]() (3.5)
(3.5)
![]() (3.6)
(3.6)
Using those new variables (3.1)-(3.6), the unknown variables vector can be presented as follows [2]:
![]() (3.7)
(3.7)
Using the notations (3.1)-(3.6) and the vector (3.7), as well as the equation (1.2), we obtain the new matrix form of the first order differential equations, which describes the motion of the rocket-launching device system:
![]() (3.8)
(3.8)
where,
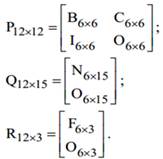 (3.9)
(3.9)
Which ![]() ,
, ![]() and
and ![]() are zeros matrices and as mentioned before other blocks are the random matrices that their elements are random values imposing the launching device during the firing. Here, we solve the matrix system (3.8) by applying radial basis functions. The 6 scalar equations are necessary to calculate the
are zeros matrices and as mentioned before other blocks are the random matrices that their elements are random values imposing the launching device during the firing. Here, we solve the matrix system (3.8) by applying radial basis functions. The 6 scalar equations are necessary to calculate the ![]() unknown variables that describe the movement of the rocket-launching device system during firing (
unknown variables that describe the movement of the rocket-launching device system during firing (![]() ) while the other scalar equations allow to compute the evolutions of the differentials of
) while the other scalar equations allow to compute the evolutions of the differentials of ![]() main unknown variables defined with (3.1)-(3.6) [2].
main unknown variables defined with (3.1)-(3.6) [2].
For solving the system matrix (3.8), we approximate the components of ![]() with the
with the ![]() interpolant (2.1) so that:
interpolant (2.1) so that:
![]() (3.10)
(3.10)
Where ![]() is constant. By differentiating from (3.10) the components of
is constant. By differentiating from (3.10) the components of ![]() obtain as follows:
obtain as follows:
![]() (3.11)
(3.11)
Substituting the equations (3.10), (3.11) in (3.8) and collocating it in same ![]() centers, we obtain
centers, we obtain ![]() system of equations with unknown parameters
system of equations with unknown parameters![]() . Therefore, one can be approximate the unknown variables
. Therefore, one can be approximate the unknown variables ![]() from equations (3.10).
from equations (3.10).
4. Numerical Results
In this Section, the proposed method based on ![]() is tested for solving the system (3.8). All results carried out with Maple software, the approximation of the components of
is tested for solving the system (3.8). All results carried out with Maple software, the approximation of the components of ![]() are shown in figural form. The
are shown in figural form. The ![]() function with the constant shape parameter
function with the constant shape parameter![]() for
for ![]() is applied for basis functions. Also the number of centers are selected so that
is applied for basis functions. Also the number of centers are selected so that ![]() . Based on theoretical and numerical experiments [7,8,9,10] it is clear that increasing
. Based on theoretical and numerical experiments [7,8,9,10] it is clear that increasing ![]() results in more accurate results. The matrices
results in more accurate results. The matrices ![]() are produced with Maple’s Random function that randomly assigns elements in interval
are produced with Maple’s Random function that randomly assigns elements in interval ![]() for the underlying matrices.
for the underlying matrices.
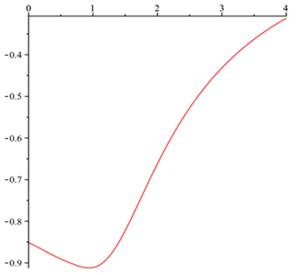
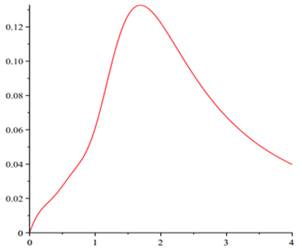
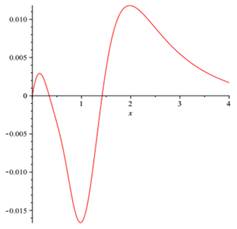
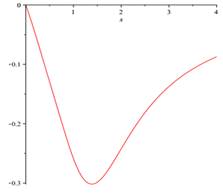
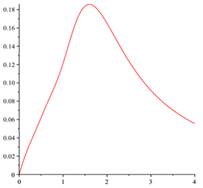
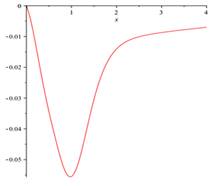
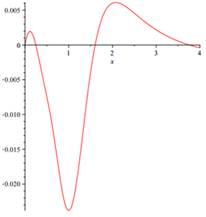
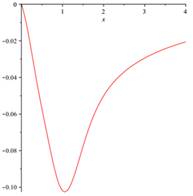
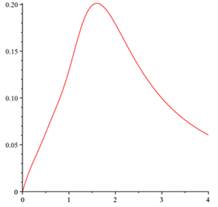
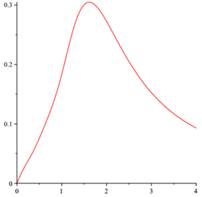
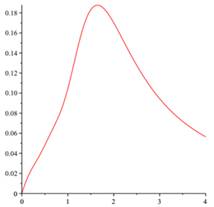
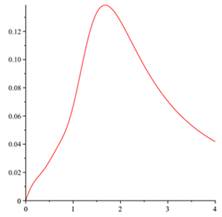
The differential oscillations parameters of rocket-launching device defined by (3.1)-(3.6) also oscillations parameters ![]() ,
, ![]() are approximated by the proposed method and the numerical results are shown in Fig. 1 and Fig. 2. Notice that by passing time (horizontal axis), the values of oscillations parameters tend to zero. It is clear that output results be different compared with those are presented for other random matrices (3.9), but according to our observations, they are similar to presented results for any random matrices.
are approximated by the proposed method and the numerical results are shown in Fig. 1 and Fig. 2. Notice that by passing time (horizontal axis), the values of oscillations parameters tend to zero. It is clear that output results be different compared with those are presented for other random matrices (3.9), but according to our observations, they are similar to presented results for any random matrices.
![]()
![]()
![]()
Fig. 1. The differential of oscillations parameters of rocket-launching device
![]()
![]()
![]()
Fig. 2. The oscillations parameters of rocket-launching device
Notations and Symbols
|
| independent unknown dynamic variables of the rocket-launching device system motion |
|
| vehicle chassis translation |
|
| chassis pitch movement |
|
| chassis rolling movement |
|
| gyration movement around the vertical axes |
|
| pitch movement |
|
| rocket translation |
|
| matrix of the coefficients for the nonlinear combinations of the unknown variables |
|
| external forces that acts on the system |
|
| shape parameter |
|
| Euclidean distance |
|
| set of centers |
|
| derivative of s |
|
| derivative of |
|
| derivative of |
|
| derivative of |
|
| derivative of |
References
- P. Somoiag, C. Moldoveanu, Numerical research on the stability of launching devices during firing, Defence Technology 9, (2013), 242-248.
- P. Somoiag, F. Moraru, D. Safta, C. Moldoveanu, A mathematical model for the motion of a rocket-launching device system on a heavy vehicle, Military technical academy, Romania, (2012).
- H. Wendland, Scattered Data Approximation, Cambridge University Press, (2005).
- M. D. Buhmann,Radial Basis Functions: Theory and Implementation, University of Gissen, Cambridge University Press, (2004).
- R. Schaback, Improved error bounds for scattered data interpolation by radial basis functions, Math Comput, 68, (1999), 201-206.
- R. L. Hardy, Multiquadric equations of topography and other irregular surfaces, J Geophys Res, 76, (1971), 1905-1915.
- R. Franke, Scattered data interpolation: tests of some methods, Math Comput, 38, (1982), 181-200.
- C. S. Huang, C. F. Lee, A. D. Cheng, Error estimate, optimal shape factor, and high precision computation of multiquadric collocation method, Eng Anal Bound Elem, 31, (2007), 614-623.
- R. E. Carlson, T. A. Foley, The parameter in multiquadric interpolation, Comput Math Appl, 21, (1991), 29-42.
- E. J. Kansa, R. E. Carlson, Improved accuracy of multiquadric interpolation using variable shape parameters, Comput Math Appl, 24, (1992), 99-120.
- E. J. Kansa, R. C. Aldredge, L. Ling. Numerical simulation of two-dimensional combustion using mesh-free methods, Eng Anal Bound Elem, 33, (2009), 940-950.
- S. A. Sarra, D. Sturgill, A random variable shape parameter strategy for radial basis function approximation methods, Eng Anal Bound Elem, 33, (2009), 1239-1245.



