Study of Free Convection in Enclosure Partially Filled with Porous Media

Mojtaba Aghajani Delavar^{1, *}, Elham Sattari²

1Corresponding Author, Faculty of Mechanical Engineering, Babol University of Technology Babol, Babol, Iran

²Faculty of Mechanical Engineering, Babol University of Technology Babol, Babol, Iran

Abstract

This study investigates the effect of porous media location over the natural convection heat transfer and related entropy generation inside a square cavity. A two dimensional lattice Boltzmann model with nine velocities was used to solve the problem numerically. The simulations were done for different Rayleigh numbers, porous part configurations and porosities. The main differences and gradients in fluid temperature take place near the hot and cold walls. Therefore in models which porous part was accumulated near these walls, fluid flow patterns were more affected by porous part and more variations were observed in comparison with clear case. In addition, these models were most sensitive to porosity. It was seen that the effect of porosity and porous part location on flow field increased for higher Rayleigh numbers. In all models it was illustrated that existence of porous media causes an increase in the amount of non-dimensional entropy generation.

Keywords

Natural Convection, Enclosure, Entropy Generation, Lattice Boltzmann Method, Porous

Received:April 8, 2015
Accepted: May 9, 2015
Published online: June 8, 2015

@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/

1. Introduction

The phenomenon of natural convection in enclosures has received considerable attention due to its importance in many applications, such as solar collectors, electronic cooling devices, building engineering, geophysical applications, etc. A review of natural convection in enclosures can be found in Oosthuizen and Naylor [1]. Fluid flow and convection heat transfer in porous media have been widely investigated numerically and experimentally due to its many important applications such as petroleum processing, catalytic and chemical particle beds, transpiration cooling, packed-bed regenerators, heat transfer enhancement, solid matrix or micro-porous heat exchangers, and many others. Many researchers studied the natural convection heat transfer in enclosures filled with porous medium by analytical, experimental and numerical methods [2,3]. El-Amin et al. [4] numerically studied the non-Darcy natural convection over a vertical flat plate in a fluid-saturated porous medium. Narayana et al. [5] investigated the free convection heat and mass transfer of non-Newtonian power law fluid from a vertical surface embedded in a doubly stratified Darcy porous medium. By considering thermal dispersion, natural convection heat transfer from a vertical flat plate embedded in a thermally stratified non-Newtonian fluid saturated non-Darcy porous medium was analyzed [6]. Kiwan and Khodier [7]used the Darcy-Brinkman-Forchheimer model along with Boussinesq approximation for numerical simulation of the steady-state, laminar, two-dimensional, natural convection heat transfer in an open-ended channel partially filled with an isotropic porous. Khan et al. [8] developed novel pool boiling enhancement technique for a passive electronics cooling design. They tested and reported a combination of surface modification by metallic coating and micro-machined porous channels attached to the modified surface.

The lattice Boltzmann method (LBM) is a powerful numerical technique based on kinetic theory for modeling the fluid flows and physics in fluids [9]. In the recent years, the lattice Boltzmann method has developed as a significant success alternative numerical approach for the solution of a large class of engineering. Several natural convection problems in clear and porous cavities have simulated successfully with the different thermal lattice Boltzmann models or other Boltzmann-based schemes [9-13]. Peng et al. [9] proposed a simplified thermal energy distribution model for natural convection in a square cavity at a wide range of Rayleigh numbers. Seta et al. [10,11] used thermal lattice Boltzmann method to study natural convection and other thermal problems in porous media. D’Orazio et al. [14] to simulate the two-dimensional natural convection flow in a cavity proposed a thermal lattice Boltzmann model with doubled populations, together with a new boundary condition for temperature and heat flux. Mezrhab et al. [15] numerically investigated the effect of a single and multiple partitions on heat transfer phenomena in an inclined square cavity, differentially heated. Jami et al. [16] a numerical investigation of laminar convective flows in a differentially heated, square enclosure with a heat-conducting cylinder was carried out by lattice Boltzmann equation for flow field.

Fluid flow and heat transfer characteristics at the interface between a porous medium and an adjacent free fluid have received considerable attention due to its wide range of engineering applications such as electronic cooling, drying processes, thermal insulation, porous bearing, solar collectors, and heat pipes. Chandesris and Jamet [17] investigated the velocity boundary condition that be imposed at an interface between a porous medium and a free fluid. Alazmi and Vafai [18] analyzed different types of interfacial conditions between a porous medium and a fluid layer. They found five primary categories of interface conditions in the literature for the fluid flow and four primary categories of interface conditions for heat transfer, more information can been found in [18].

Optimized design of heat systems can be obtained within minimizing of entropy generation. Entropy generation is associated with thermodynamic irreversibility, which exists in all heat transfer processes. This field was attending greatly at fields such as cross flow heat exchangers, power plants, energy storage systems, and refrigeration usages. For optimizing the working conditions, a set of design parameters can be obtained for a specified thermal system. Notable researches have been done to investigate importance of entropy generation in thermal systems. The early works for optimization design with minimizing the entropy generation have been done by Bejan [19-21]. In Sahin [22] worka comparative study of entropy generation inside of ducts with different shapes and determination of optimum duct shape subjected to isothermal boundary condition have been done. Mahmud and Fraser [23] applied the second law analysis to fundamental convective heat transfer problems. Al¨boud-Saouli et al. [24] investigated entropy generation in a laminar liquid flow inside a channel made of two parallel heated plates under the action of transverse magnetic field.

Heidary et al. [25] numerically studied the free convection and entropy generation in an inclined square cavity filled with a porous medium and the effect of a partition on the bottom wall. They show that the partition can be used as a control element for heat transfer, fluid flow and entropy generation.

In the author previously works [12,13] the lattice Boltzmann method were employed to investigate the effect of the heater location on flow pattern, heat transfer and entropy generation in a cavity. Results showed that the location of heater and Rayleigh number have great effects on the flow pattern and temperature field in the enclosure and subsequently on entropy generation. Mehrizi et al. [26] investigated heat transfer and fluid flow in a porous media cold plate using lattice Boltzmann method and they investigated effect of porosity on heat transfer from the fins surfaces was studied at different Reynolds and Prandtl numbers. Salehi et al. [27] placed a set of porous arrays with square cross section at specific location of channel and investigated pressure drop and Nusselt number in this channel.

In addition to Lattice Boltzmann Method, analytical methods have been used for the study of influence of porous media on the fluid flow and heat transfer [28-31].

In this study, the effects of porosity, porous medium location and Rayleigh number on overall heat transfer and entropy generation inside the square enclosure were investigated. A 2D thermal lattice Boltzmann method with 9 velocities, D2Q9, was used to solve the thermal flow problem. The simulations in each configuration were made for Rayleigh numbers changing from 10³ to 10⁶. Then in all simulations, entropy generation was calculated and the second law analysis was used to compare different geometries.

2. The Lattice Boltzmann Method

In this study, the D2Q9 model was used. After introducing Bhatnagar–Gross–Krook approximation (BGK), the general form of lattice Boltzmann equation with external force is written as [32]:

             (1)

where ,,, and are equilibrium distribution, discrete lattice velocity in k direction, external force, lattice relaxation time and lattice time step, respectively, and k and show streaming direction and equilibrium. The equilibrium distribution function is calculated with:

        (2)

where , and are velocity vector, density and weighting factor. To consider both the flow and the temperature fields, the thermal LBM utilizes two distribution functions, and, for flow and temperature fields respectively. The distribution function is as same as discussed above; the  distribution function is as below:

                (3)

The corresponding equilibrium distribution functions are defined as [12,13,32]:

           (4)

Having computed the values of these local distribution functions, the flow properties are defined as:

        (5)

where the sub-index i denotes the component of the Cartesian coordinates and  is Temperature.

The temperature differences are small as enough () to use the Boussinesq approximation and neglecting the radiation heat transfer.is thermal expansion coefficient. In order to incorporate buoyancy force in the model, the force term in the Eq. (1) needs to are calculated as below in vertical direction (y):

              (6)

To simulate the natural convection problems with the LBM, it is necessary to determine the characteristic velocity  and then to obtain the corresponding kinetic viscosity (), thermal diffusivity () and duct width (H). It implies that for different Rayleigh numbers both the kinetic viscosity and thermal diffusivity cannot be fixed as constants in LBM simulations if the characteristic velocity is kept constant (more information in Kao et al., [33]).

The Brinkman-Forchheimer equation which has been used successfully in simulation of porous media in wide range of porosities, Rayleigh, Reynolds and Darcy numbers [7,10,11]was used for simulation the flow in porous regions, which is written as:

              (7)

Where ,and are porosity, pressure and kinetic viscosity . The last term in the right hand in the parenthesis is the total body force, F, which was written by using the widely used Ergun’s relation [32]. For porous medium, the corresponding distribution functions are as same as Eq. (1). However, the equilibrium distribution functions are calculated by:

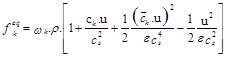       (8)

In Eq. (1) the best choice for the forcing term,, to achieve correct equation of hydrodynamics in porous zones is taking [15]:

     (9)

After improving Eq. (6) as below it can be used for both fluid and porous zones:

                  (10)

The matching conditions at the fluid-porous interface are thus satisfied automatically due to this unified governing equation. So employing LBM significantly reduces the complexity of the traditional methods, which considers two regions separately.

According to above equations, is related to , so the Eq. (9) is nonlinear for the velocity. Guo and Zhao (2002) presented a temporal velocity  to solve this nonlinear problem as follows:

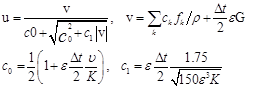  (11)

where d is diameter. The permeability of porous media is calculated by [35]:

               (12)

where represents the solid structure particles diameter. is hot wall temperature,To proper investigation of conjugate convection and conduction heat transfer in porous medium, the effective thermal conductivity of the porous media, , should be identified, which was calculated by [36]:

      (13)

where  is fluid conductivity, represents solid structure conductivity.

3. Boundary Conditions

The unknown distribution functions are those toward the domain because of the fact that from the streaming process, the distribution functions out of the domain are known. Regarding the boundary conditions of the flow field, the bounce-back scheme is applied for the solid walls which assumed no slip. This scheme specifies the outgoing directions of the distribution functions as the reverse of the incoming directions at the boundary sites. In addition, for the temperature field, the local temperature is defined as in Eq. (5). The treatment of the temperature population (i.e. the distribution function) at the adiabatic walls can be simplified by applying the bounce-back scheme such that a ‘‘heat flux-free state" is obtained in each lattice direction for the specific nodes. Applying this treatment for adiabatic walls yields (for bottom adiabatic boundary):

    (14)

where is the lattice on the boundary and , denotes the lattice inside the cavity adjacent to the boundary. For isothermal boundaries such as left side, hot wall, the unknown distribution functions were evaluates as:

           (15)

More information about boundary condition in LBM can be found in [32].

4. Entropy Generation

Volumetric entropy generation due to heat transfer,, due to friction, , and the total volumetric entropy generation,  are calculated as below:

                    (16)

is molecular viscosity. The non-dimensional entropy generation rates,, and  in whole domain are defined by:

                      (17)

is heat transferred from wall. Above equations were used in both clear and porous zones.

5. Computational Domain and Validation

The computational domain is a square cavity in which the left and right side walls are isotherms, the hot and the cold walls, respectively. Upper and bottom walls are adiabatic. Half of the cavity is filled with porous media. The porous part is located at different positions in the enclosure (Fig. 1). Although the models "LEFT" and ‘RIGHT’ seem to be symmetrical, but results illustrated that they are different specially regarding to thermal filed and entropy generation.

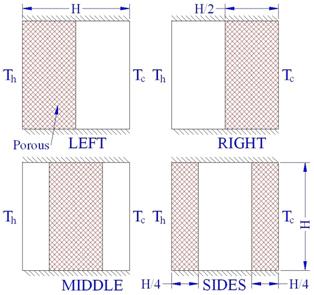
Figure 1. Schematic of concerning geometries in different models.

In this study, the Rayleigh number changes between to. For different porosities, 0.4, 0.6, 0.8 and 1.0 (no porous) the simulations have been carried out. In all models the temperature difference between the hot and the cold walls, Prandtl number and permeability were fixed at, 0.71 and 10^-7m^-2, respectively. In this study, the  (in Eq. (13)) was set 0.1. In simulations, the variations of Rayleigh number were adjusted by changing the value of in Eq. (6).

Local and average Nusselt numbers were defined on isothermal walls in y directions as below:

    (18)

is the hot wall temperature, is the cold wall temperature. The numerical simulation was done by an in house LBM code, which was written in FORTRAN. This code was validated for the problem of natural convection within a 2D clear square cavity. For validation and grid independency, the averaged Nusselt numbers were calculated at different Rayleigh numbers in different grid points. Table 1 shows the computed averaged Nusselt numbers in comparison with previous works (Kao et al. [33] and De Vahl Davis [37]) for the grid point from to . It is due to the results of the Table 1; the grid point was selected for all numerical simulations.

Table 1. Comparison of averaged Nusselt numbers computed at different Rayleigh numbers using different grids with results presented in De Vahl Davis [37] and Kao et al. [33].

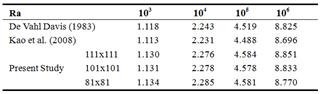
Table 2 compares well results for simulation of free convection in cavity filled with porous media at different Rayleigh numbers with those of Seta et al. [10] and Nithiarasu et al. [38].

Table 2. Comparison of averaged Nusselt numbers for free convection in porous cavity computed at different Rayleigh numbers using different grids with results presented in Seta et al.[10] and Nithiarasu et al. [38], Da=0.01, Pr=1.0.

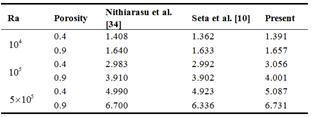
Figure 2 compares well velocity profile in clear and porous regions and porous fluid interface in LB model and Alazmi and Vafai [18].

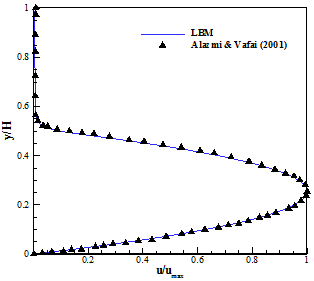
Figure 2. Comparison of velocity profile for partially filled channel with porous media between present model and Alazmi and Vafai [18].

A convergence criterion was defined as below for each concerned variable ():

               (19)

whichand are the iteration number and variable in simulation.

6. Results and Discussion

In this study, the lattice Boltzmann method is used to investigate the effect of porous media location and its porosity over the natural convection heat transfer and entropy generation inside a square cavity at different Rayleigh numbers.

Streamlines of all models at different porosities at are drawn in Fig. 3. In Fig 4 the streamlines for different Rayleigh numbers at fixed porosity () are shown. The solid matrix of porous media affects the velocity field in the cavity, so the porous media location has great effects on flow pattern, Figs. 3 and 4.

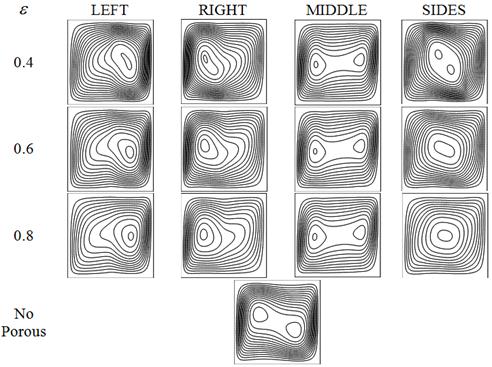
Figure 3. Streamlines for different models at different porosities for .

Due to density variation with temperature, the buoyancy force acts as motive force for fluid flow in natural convection. The main differences in fluid temperature take place near the hot and cold walls. So in models in which porous parts are accumulated near theses surfaces (models LEFT and RIGHT) fluid flow pattern is more affected by porous part and more variation is observed in comparison with clear case, also these models are most sensitive to porosity (Fig. 3). Due to symmetry in porous media location at models MIDDLE and SIDES, flow pattern is more similar to clear case. With increasing the flow velocity the effect of porous media increases (Eqs. 7&9) so it can be observed that in all models the effect of porosity and porous part location on flow field increases for higher Rayleigh numbers, Fig. 4.

In Fig. 5 the isotherms are drawn for different models at.

Figure 4. Streamlines for different models at different Rayleigh numbers for .

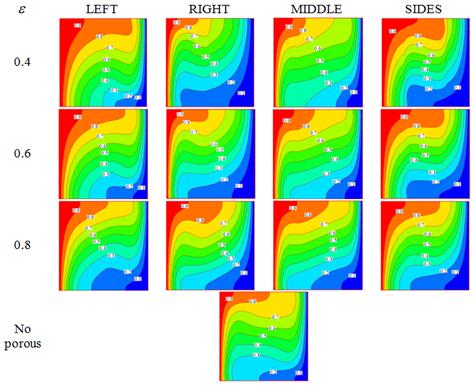
Figure 5. Isotherms for different models at different porosities for .

Isotherms for different models at are shown in Fig. 6. The same manner, as discussed for flow pattern, was observed for temperature fields; for higher values of Rayleigh numbers the porosity effects increase. As illustrated in Figs 4 and 5, it is important that porous media is located near the left hot wall or the right cold wall, and these models do not treat symmetrically.

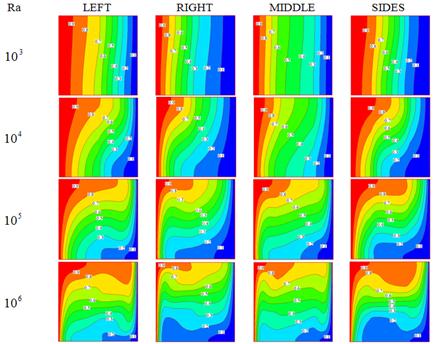
Figure 6. Isotherms for different models at different Rayleigh numbers for .

Figure 7 shows the effect of Rayleigh number and porosity on averaged Nusselt number ratio in different models.

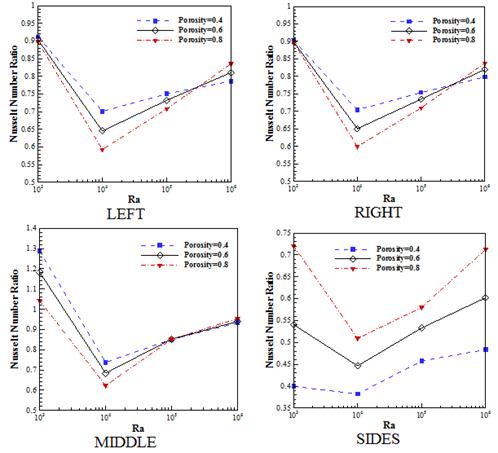
Figure 7. Averaged Nusselt Number ratio variation with Rayleigh number for different models and different porosities.

The averaged Nusselt number ratio is calculated using:

         (20)

In Fig. 8 the effect of porous part location on averaged Nusselt number for different porosities is shown. Porous media has two different effects on heat transfer in the enclosure, the first one is the presence of solid matrix and its weakening effects on the flow pattern and as a consequence on the heat transfer (convection). The second one is the change (increase) of effective thermal conductivity due to solid matrix of porous media and its positive effects on the overall heat transfer (conduction).

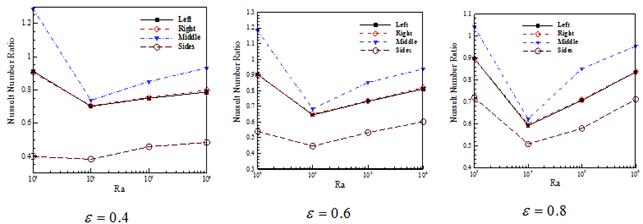
Figure 8. Averaged Nusselt number ratio variation with Rayleigh number and different porosities.

In low Rayleigh numbers the dominant heat transfer regime is conduction, because of the fact that the velocity of the fluid is low, the porous media has less effect on heat transfer, therefore the difference between different models and the clear cavity comes to minimum (Figs. 7 and 8). By increasing the Rayleigh number, the quota of conduction in overall heat transfer mechanism reduces and convection becomes as the governing heat transfer mechanism. This change takes place approximately at, so a minimum is observed for averaged Nusselt number ratio in Figs. 7 and 8. It is observed that more increasing the Rayleigh numbers, leads to increasing averaged Nusselt number due to stronger flow field in the cavity and more streamlines accumulation near the walls (Figs. 3 and 4).

When porous parts are close to hot or cold walls, the fluids velocity decreases so the temperature and velocity gradients and the Nusselt number decrease, which leads to the Nusselt number ratio less than 1. The model MIDDEL has the largest Nusselt number because that porous part is in a distance from hot and cold walls, which makes the flow field near the walls more similar to clear cavity. At low Rayleigh number, as discussed above, the governing heat transfer mechanism is conduction, so the porous media increases the effective thermal conductivity, and higher heat transfer and Nu number ratio are achieved for this model rather than clear cavity (averaged Nusselt number greater than 1 in Fig. 7 and 8).

In Fig. 8, a comparison has been made between different models in different porosities. The LEFT and RIGHT models are seen as an accumulation of porous materials besides of hot or cold walls, therefore Nusselt numbers are similar. In the MIDDEL model the porous parts are far from the hot and cold walls. Therefore, their Nusselt number is similar to clear model. However, due to the accumulation of porous parts nearby both the hot and cold walls, the SIDES model has the least Nusselt number in comparison to clear model.

In all models, it can be seen that higher values of porosity leads to lower values of Nusselt number. It is due the fact that increasing the porosity causes lower effective thermal conductivity and heat transfer rate (conduction) near the walls. It can be seen that for higher values of Rayleigh number the differences between the models is more considerable.

The average entropy generation ratio is calculated using:

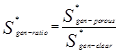                 (21)

Figure 9 shows the change of non-dimensional entropy generation ratio in different models with Rayleigh number for different porosities.

In Fig. 10 the change of non-dimensional entropy generation is compared between different models for different porosities. According to Figs. 9 and 10, the models that porous part is nearby the hot wall (SIDE and LEFT models) are similar, the non-dimensional entropy generation decreases due to an increase in porosity and the Rayleigh number. This amount in MIDDLE and SIDES models decreases when the non-dimensional entropy generation increases and in MIDDLE model when the Rayleigh number increases the non-dimensional entropy generation also increases and RIGHT model this amount first decreases then increases.

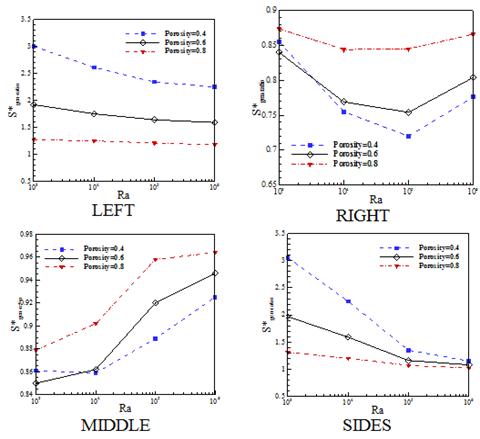
Figure 9. Averaged non-dimensional entropy generation ratio variation with Rayleigh number for different models and different porosities.

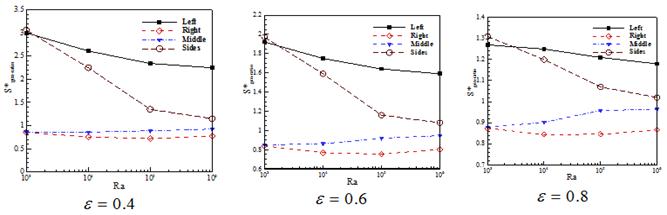
Figure 10. Averaged non-dimensional entropy generation ratio variation with Rayleigh number and different porosities.

In all models, the porous media causes an increase in the amount of non-dimensional entropy generation.

7. Conclusion

Because of density variation of fluid with temperatures, the buoyancy force acts as motive force for fluid flow in natural convection. The main differences in fluid temperature take place near the hot and cold walls; as a consequence, in models in which porous parts are accumulated near theses surfaces, the fluid flow pattern is more affected by porous part and more variation is observed in comparison with clear enclosure. In addition, these models are most sensitive to porosity. Due to symmetry in porous media location at models MIDDLE and SIDES, flow patterns are more similar to clear case. With increasing the flow velocity, the effect of porous media is increased, as a result it can be observed that in all models the effect of porosity and porous part location on flow field increases for higher Rayleigh numbers. It can be seen that increasing the Rayleigh number leads to increasing averaged Nusselt number due to change in flow pattern. In low Rayleigh numbers the dominant heat transfer regime is conduction, because the velocity of the fluid is low, the porous media has fewer effect on heat transfer, therefore the difference between different models and the clear cavity comes to minimum. The LEFT and RIGHT models can be seen as accumulation of porous materials adjacent to hot or cold walls, therefore Nusselt numbers are similar. In MIDDEL model because the porous mediums are relatively far from the hot and cold walls, the Nusselt number is similar to clear model. But the SIDES model has the smallest amount of Nusselt number in comparison to clear model because of the accumulation of porous material nearby both the hot and cold walls. In all models the existence of porous media causes an increase in the non-dimensional entropy generation. All these conclude to the fact that porous media have significant effects on the flow and thermal fields, heat transfer and so on entropy generation.

Nomenclature

 - Discrete lattice velocity in direction,

 - Diameter

 - External force

 - Equilibrium distribution.

 - Duct width

 - Convective heat transfer coefficient,

 - Permeability

 - Thermal conductivity

 - Knudsen number,

 - Mach number,

 - Local Nusselt number,

 - Pressure,

 - Prandtl number,

 - Heat Transfer,

 - Rayleigh number,

 - volumetric entropy generation rate,

 -Temperature,

 - Velocity vector,

 - Horizontal and vertical components of velocity,

 - Characteristic velocity of natural convection,

Greek Symbols

 - Thermal diffusivity,

 - Thermal expansion coefficient

 - Porosity

 - Variable in simulation

 - Molecular viscosity

 - Kinetic viscosity,

 - Density,

 - Lattice relaxation time

 - Weighting factor

 - Lattice time step

Subscripts and Superscripts

 - Reference value

 - Cold

 - Total generated

 - Hot

 - Iteration number

 - Due to heat transfer

 - Due to friction

 - Particle

 - Streaming direction

 - i direction

 - y direction

 - Equilibrium

References

1. Oosthuizen, P.H., Naylor, D., Introduction to Convective Heat Transfer Analysis. McGraw-Hill, New York, 1992.
2. Ingham, D.B., Pop, I.,Transport Phenomena in Porous Media II, Pergamon, 2005.
3. Nield, D.A., Bejan, A.,Convection in Porous Media,Second ed., Springer, NY, 2006.
4. El. Amin, M. F., Abbas, I., Gorla, R. S. R.,Boundary Layer Natural Convection in a Fluid Saturated Porous Medium Using Finite Element Method, Int. J. Fluid Mechanics Research, Vol. 35, no. 5, pp. 445-458, 2008.
5. Narayana, P. A. L., Murthy, P. V. S. N., Krishna, S. S. R., Postelnicu, A.,Free Convective Heat and Mass Transfer in a Doubly Stratified Porous Medium Saturated with a Power-Law Fluid, Int. J. Fluid Mechanics Research, Vol. 36, No. 6, pp. 524-537, 2009.
6. Kairi, R. R., Murthy, P. V. S. N.,Free Convection in a Thermally Stratified Non-Darcy Porous Medium Saturatedwith a Non-Newtonian Fluid, Int. J. Fluid Mechanics Research, Vol. 36, no. 5, pp. 414-423, 2009.
7. Kiwan, S.,Khodier, M.,Natural Convection Heat Transfer in an Open-Ended Inclined Channel-Partially Filled with Porous Media, Heat Transfer Engineering, , no.1, pp. 67-75, 2008.
8. Khan, N., Toh, K. C.Pinjala, D.,Boiling Heat Transfer Enhancement Using Micro-Machined Porous Channels for Electronics Cooling, Heat Transfer Engineering,Vol. 29, no. 4, 2008, DOI: 10.1080/01457630701825481
9. Peng, Y., Shu, C., Chew, Y.T.,Simplified thermal lattice Boltzmann model for incompressible thermal flows, Physical Review E 68, pp. 026701, 2003.
10. Seta, T., Takegoshi, E., Okui, K.,Lattice Boltzmann simulation of  natural convection in porous media, Mathematics and Computers in Simulation, Vol. 72, no.2-6, pp. 195–200, 2006.
11. Seta, T., Takegoshi, E., Kitano, K., Okui, K.,Thermal Lattice Boltzmann Model for Incompressible Flows through Porous Media,  Journal of Thermal Science and Technology, Vol. 1, no. 2, pp. 90-100, 2006.
12. Delavar, M.A., Farhadi, M., Sedighi, K.,Effect of the heater location on heat transfer and entropy generation in the cavity using the lattice Boltzmann Method, Heat Transfer Research, Vol. 40, no. 6, pp. 521-536, 2009.
13. Delavar, M.A., Farhadi, M., Sedighi, K.,Effect of discrete heater at the vertical wall of the cavity over the heat transfer and entropy generation using LBM, Thermal Science, in press, 2011,doi:10.2298/TSCI090422035A
14. D’Orazio, A., Corcione, M., Celata, G.P.,Application to natural convection enclosed flows of a lattice Boltzmann BGK model coupled with a general purpose thermal boundary condition, Int. J. Thermal Sciences, Vol. 43, no. 6, pp. 575–586, 2004.
15. Mezrhab, A., Jami, M., Abid, C., Bouzidi, M., Lallemand, P.: Lattice-Boltzmann modeling of natural convection in an inclined square enclosure with partitions attached to its cold wall. Int. J. Heat and Fluid Flow 27 (3). 456–465 (2006)
16. Jami, P., Mezrhab, A., Bouzidi, M., Lallemand, P.,Lattice Boltzmann method applied to the laminar natural convection in an enclosure with a heat-generating cylinder conducting body, Int. J. Thermal Sciences, Vol. 46, no. 1, pp. 38–47, 2007.
17. Chandesris, M., Jamet, D.,Boundary conditions at a planar fluid–porous interface for a Poiseuille flow, Int. J. Heat and Mass Transfer, Vol. 49, pp. 2137–2150, 2006.
18. Alazmi, B., Vafai, K.,Analysis of fluid flow and heat transfer interfacial conditions between a porous medium and a fluid layer, Int. J. Heat and Mass Transfer, Vol. 44, pp. 1735-1749, 2001.
19. Bejan, A.,Entropy generation minimization, New York: CRC Press, 1996.
20. Bejan, A.,Advanced engineering thermodynamics, 2nd ed., New York: Wiley, 1997.
21. SEKULIC, D. P., Entropy Generation in a Heat Exchanger, Heat Transfer Engineering, Vol. 7, no. 1-2,pp. 83-88, 1986.
22. Sahin, A.Z.,A second-law comparison for optimum shape of duct subjected to constant wall temperature and laminar flow, Heat and Mass Transfer, Vol. 33, no. 5-6, pp. 425–30, 1998.
23. Mahmud, S., Fraser, R.A.,The second-law analysis in fundamental convective heat-transfer problems, Int. J. Thermal Sciences, Vol. 42, no. 2, pp. 177–86, 2003.
24. Al¨boud-Saouli, S., Settou, N., Saouli, S., Mezrab, N.,Second-law analysis of laminar fluid flow in a heated channel with hydromagnetic and viscous dissipation effects, Applied Energy, Vol. 84, no. 3, pp. 279–289, 2007.
25. Heidary, H.,Pirmohammadi, M.,Davoudi, M.,Control of Free Convection and Entropy Generation in Inclined Porous Media, Heat Transfer Engineering, 2011, DOI:10.1080/01457632.2012.624875
26. Mehrizi, A., et al. "Lattice Boltzmann Simulation of Heat Transfer Enhancement in a Cold Plate Using Porous Medium." Journal of Heat Transfer 135.11 (2013): 111006.
27. Salehi, A., Abbassi. A., and Nazari, M. "Numerical Solutionof Fluid Flowand Conjugate Heat Transferina Channel Filledwith Fibrous Porous Media-a Lattice Boltzmann Method Approach." Journal of Porous Media 17.12 (2014).
28. Meher .R., Mehta M. N., and Meher S. K. (2010) Adomian Decomposition Approach to Fingero-Imbibition Phenomena in Double Phase Flow through Porous Media. Int. Journal of Applied Maths and Mech. 6 (9): 34-46.
29. Meher. R (2010). Adomian Decomposition Method for Dispersion Phenomena Arising in Longitudinal Dispersion of Miscible Fluid Flow through Porous Media.
30. V.N. Mishra, Some Problems on Approximations of Functions in Banach Spaces, Ph. D. Thesis (2007), Indian Institute of Technology, Roorkee- 247667, Uttarakhand, India.
31. V.N. Mishra, M.L. Mittal, U. Singh, On best approximation in locally convex space, Varāhmihir Journal of Mathematical Sciences India, Vol. 6, No.1, (2006), 43-48.
32. Mohammad, A.A.,Farhadi, M., Sedighi, K., &Aghili, A. LLattice Boltzmann Method, Fundamentals and Engineering Applications with Computer Codes, Springer-Verlag London Limited, 2011.
33. Kao, P.H., Chen, Y.H., Yang, R.J.,Simulations of the macroscopic and mesoscopic natural convection flows within rectangular cavities, Int. J. Heat and Mass Transfer, Vol. 51, no. 15-16, pp. 3776–3793, 2008.
34. Ergun, S.,Flow through packed columns, Chemical Engineering Prog., Vol. 48, no. 2, pp. 89–94, 1952.
35. Kaviany, M.,Principles of Heat Transfer in Porous Media, Springer-Verlag, New York, 1991.
36. Zehener, P.,Waermeleitfahigkeit won Schuettungen be MassigenTemperaturea, Chem.-Ingr.-Tech., Vol. 42, pp. 933–941, 1970.
37. De Vahl Davis, G.,Natural convection of air in a square cavity: a bench mark numerical solution, Int. J. Numerical Methods in Fluids, Vol. 3, no. 3, pp. 249–264, 1983.
38. Nithiarasu, P., Seetharamu, K.N., Sundararajan, T.,Natural convective heat transfer in a fluid saturated variable porosity medium, Int. J. Heat Mass Transfer, Vol. 40, no. 16, pp. 3955–3967, 1997.