A Mathematical Theorem in Triply-Diffusive Convection

Hari Mohan^*, Pardeep Kumar

Department of Mathematics, ICDEOL, Himachal Pradesh University, Summer Hill Shimla-5, India

Abstract

A mathematical analysis of the governing equations of triply diffusive fluid layer with one of the components as heat with diffusivity κ, prescribes upper limit for the complex growth rate of oscillatory motions of neutral or growing amplitude in such a manner that it naturally culminates in sufficient conditions precluding the non- existence of such motions. Further, the results derived herein are uniformly valid for quite general nature of bounding surfaces.

Keywords

Triply Diffusive Convection, Rayleigh Numbers, Lewis Number, Prandtl Number

Received: April 7, 2015
Accepted: April 25, 2015
Published online: June 18, 2015

@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/

1. Introduction

Thermohaline convection or more generally double diffusive convection has matured into a subject possessing fundamental departure from its counterpart, namely single diffusive convection, and is of direct relevance in the fields of oceanography, astrophysics, limnology and chemical engineering etc. For a broad and a recent view of the subject one may be referred to Brandt and Fernando [1]. Two fundamental configurations have been studied in the context of thermohaline instability problem, the first one by Stern [2] wherein the temperature gradient is stabilizing and the concentration gradient is destabilizing and the second one by Veronis [3] wherein the gradient is destabilizing and the concentration gradient is stabilizing. The main results derived by Stern and Veronis for their respective configurations are that both allow the occurrence of a stationary pattern of motions or oscillatory motions of growing amplitude provided the destabilizing concentration gradient or the temperature gradient is sufficiently large. However, stationary pattern of motion is the preferred mode of setting in of instability in case of Stern’s configuration whereas oscillatory motions of growing amplitude are preferred in Veronis’ configuration. More complicated double-diffusive phenomenon appears if the destabilizing thermal/concentration gradient is opposed by the effect of magnetic field or rotation.

The derivation of upper limits for the linear growth rate of a disturbance in thermohaline convection problems is an important problem especially when both the boundaries are not dynamically free so that exact solutions in closed form are not obtainable and one has to depend on numerical solutions which are rather laborious. In this situation, derivation of certain integrals estimates acquire great importance, for, they enable us to obtain sufficient conditions of stability and define a possible range of parameters for growing perturbations in case of instability. For further study one may be referred to Banerjee et al. [4] and Gupta et al. [5]. Mohan and Anjula [6] derived upper limits for the complex growth rate of an arbitrary oscillatory perturbation which may be neutral or unstable for Veronis’ and Stern’s thermohaline configurations which in particular yield sufficient conditions for the validity of "principle of exchange of stabilities" for these configurations and their results are uniformly valid for all combinations of dynamically free or rigid boundaries .Mohan [7] investigated the problem of thermohaline convection coupled with cross-diffusions for the Veronis type configuration and derived a semi-circle theorem that prescribed upper limits for the complex growth rate of oscillatory motions of neutral or growing amplitude in such a manner that it naturally culminates in sufficient conditions precluding the non- existence of such motions.

All the above researchers have considered the case of two component systems. However, it has been recognized later on by Griffiths [8], Turner [9] that there are many situations wherein more than two components are present. Examples of such multiple diffusive convection fluid systems include the solidification of molten alloys, geothermally heated lakes, magmas and their laboratory models and sea water. Griffith [8], Pearlstein et al. [10] and Lopez [11] have theoretically studied the onset of convection in a horizontal layer, of infinite extension of a triply diffusive fluid (where the density depends on three independently diffusing agencies with different diffusivities). These researchers found that small concentrations of a third component with a smaller diffusivity can have a significant effect upon the nature of diffusive instabilities and oscillatory and direct salt finger modes are simultaneously unstable under a wide range of conditions, when the density gradients due to components with the greatest and smallest diffusivity are of same signs .Some fundamental differences between the double and triply convection are noticed by these researchers diffusive. Among these differences, one is that if the gradients of two of the stratifying agencies are held fixed ,then three critical values of the Rayleigh number of the third agency are sometimes required to specify the linear stability criteria(only one critical number is required in double diffusive convection ) . Another difference is that the onset of convection may occur via a quassiperiodic bifurcation from the motionless basic state. Terrones [12] studied the effect of cross-diffusion on the stability criteria in a triply diffusive system. Ryzhkov and Shevtsova [13] studied the case of multicomonent mixture with application to thermo gravitational column. Ryzhkov and Shevtsova [14] also studied the long wave instability of a multicomponent fluid with Soret effect. Rionero [15] studied a triply convective diffusive fluid mixture saturating a porous horizontal layer, heated from below and salted from above and obtained sufficient conditions for inhibiting the onset of convection and guaranteeing the global nonlinear stability of the thermal conduction solution. Rionero [16] also investigated the multicomponent diffusive convection in porous layer for the more general case when heated from below and salted by m salts partly from above and partly from below. Zhao, Wang and Zhang [17] investigated the problem of triply diffusive convection in Maxwell fluid saturated porous layer and obtained the criterion for the onset of stationary and oscillatory convection. Shivkumara and Kumar [18] investigated the bifurcation analysis of a triply diffusive coupled stress fluid in terms of a simplified model consisting of seven nonlinear ordinary differential equations. Shivkumara and Kumar [19] have studied the linear and weakly nonlinear triple diffusive convection in a couple stress fluid layer.

Motivated by these considerations, the present paper derives semi-circle theorems that prescribe upper limits for the complex growth rate of oscillatory motions of neutral or growing amplitude in such a manner that it naturally culminates in sufficient conditions precluding the non- existence of such motions in a triply diffusive fluid layer with one of the components as heat with diffusivity . Further, the results derived herein are uniformly valid for quite general nature of bounding surfaces.

2. Mathematical Formulation and Analysis

A viscous and finitely heat conducting Boussinesq fluid is statically confined between two horizontal boundaries z=0 and z=d of infinite horizontal extension and finite vertical depth which are respectively maintained at uniform temperatures  and uniform concentrations.

Following Griffiths [8] and Banerjee et al. [4], the relevant governing equations and boundary conditions for the triply diffusive convection in their non-dimensional form are given by:

   (2.1)

,                  (2.2)

,                (2.3)

,               (2.4)

together with the boundary conditions

 at z =0 and z =1   (2.5)

(both boundaries rigid)

or

  at z =0 and z =1 (2.6)

(both boundaries dynamically free)

or  at z =0

and

 at  z =1 .      (2.7)

(lower boundary rigid and upper boundary dynamically free)

or  at z =0

and

 at z =1.           (2.8)

(lower boundary free and upper boundary dynamically rigid)

The meanings of symbols from physical point of view are as follows;

z is the vertical  coordinate, is differentiation along the vertical direction, a² is square of horizontal wave number, σ  is the Prandtl number,  are the Lewis numbers for the two concentrations respectively,  is the thermal Rayleigh number, are the concentration Rayleigh numbers for the two concentration components, p = p_r + ip_i is complex growth rate such that p_r and p_i are real constants, w is the vertical velocity,  is the temperature,  are the respective concentrations of the two components.

We now prove the following theorem:

Theorem 1: If (p, w,,), p = p_r + ip_i, p_r ≥ 0  is a non -trivial solution of equations (2.1)–(2.4) together with one of the boundary conditions (2.5)-(2.8) with,,  , then

,

where

.

Proof: Multiplying equation (2.1) by w* (the complex conjugate of w) and integrating the resulting equation over the vertical range of z, we get

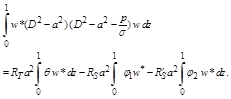     (2.9)

Taking the complex conjugate of equations (2.2) (2.3) and (2.4) and using the resulting equations in equation (2.9), we get

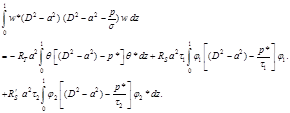 (2.10)

Integrating equations (2.10) by parts a suitable number of times, using either of the boundary conditions (2.5)-(2.8) and one of the following inequalities

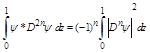,            (2.11)

where,

 for n = 0, 1 and for n = 0, 1, 2,

we have

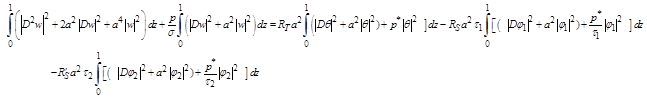
Equating the real and imaginary parts of equation (2.11) equal to zero and using, we get

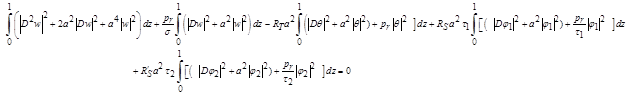  (2.12)

and

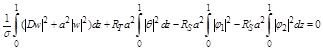                  (2.13)

Multiplying equation (2.13) by and adding the resulting equation to (2.12), we have

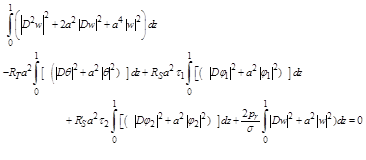            (2.14)

Equation (2.13) implies that

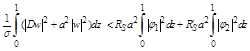     (2.15)

Since   vanish at z = 0 and z = 1, therefore Rayleigh-Ritz inequality [20] yields

              (2.16)

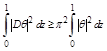            (2.17)

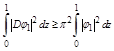              (2.18)

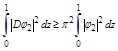            (2.19)

Combining inequalities (2.15) and (2.16), we get

 (2.20)

or

which implies that

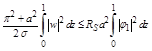              (2.21)

And

               (2.22)

Also upon using inequalities (2.18) and (2.19) respectively, we have

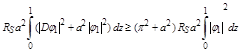     (2.23)

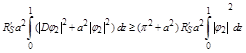    (2.24)

Combining inequalities (2.21) and (2.23), we have

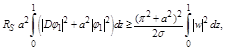      (2.25)

and combining inequalities (2.22) and (2.24), we get

.  (2.26)

Further, utilizing Schwartz inequality, we have

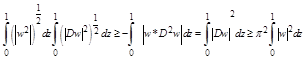 (using)(2.16)

which on simplification yields

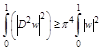                 (2.27)

Inequality (2.16) together with inequality (2.24) yields

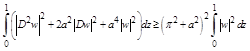     (2.28)

Multiplying equation (2.2) by the complex conjugate of equation (2.2) and integrating the resulting equation over the vertical range of z, we get

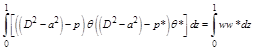
Integrating the above equation by parts an appropriate number of times and using either of the given boundary conditions, we get

 (2.29)

Since, therefore from equation (2.29), we have

         (2.30)

Also emulating the derivation of inequalities (2.24) and (2.25) we derive the following inequality

 (2.31)

Using inequality (2.28) in equality (2.27), we get

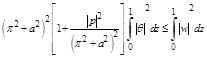        (2.32)

Now,

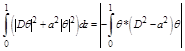
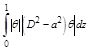
(using Schwartz inequality)

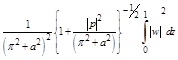
      (2.33)

(using inequalities (2.28) and (2.29) )

Making use of inequalities (2.25), (2.26), (2.28) and (2.33), equation (2.14) yields

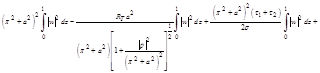 + < 0           (2.34)

Since,, it follows from inequality (2.34) that

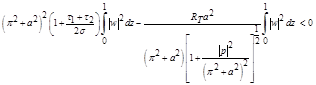
or

. (2.35)

Since, minimum value of  with respect    is  it follows from inequality (2.35) that

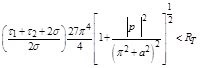
or

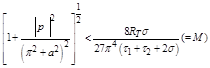      (2.36)

Therefore, we have

                (2.37)

Further, since 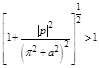, therefore it follows from inequality (2.35) that

           (2.38)

Now, the maximum value of  with respect to  is, therefore inequality (2.38) yields

            (2.39)

Using inequality (2.39) in inequality (2.37), we get

.

This completes the proof of the theorem.

Theorem 1 from the point of view of hydrodynamic stability theory may be stated as:

The complex growth rate of an arbitrary oscillatory perturbation of growing amplitude () in triply diffusive convection problem lies inside a semi- circle in the right-half of the - plane whose centre is at the origin and whose radius is

.

Corollary 1. If (p, w, , ),  p = p_r + ip_i, p_r ≥ 0  is a non -trivial solution of equations (2.1)– (2.4) together with one of the boundary conditions (2.5)-(2.8) with,,  and M  , then .

Proof. Follows from Theorem 1.

Corollary1 implies that oscillatory motions of growing amplitude are not allowed in triply

diffusive convection problem if M  .

3. Conclusions

In the present paper, triply diffusive convection problem is considered. The investigation of triply diffusive fluid layer with one of the components as heat with diffusivity is motivated by its interesting complexities as a thremosolutal or double diffusive phenomenon which has its importance in various fields such as high quality crystal production, oceanography, production of pure medication, solidification of molten alloys, exothermally heated lakes and magmas. The analysis made brings out the following main conclusions:

(i) The complex growth rate of an arbitrary oscillatory perturbation of growing amplitude () in triply diffusive convection problem lies inside a semi- circle in the right-half of the - plane whose centre is at the origin and whose radius is

.

(ii) The oscillatory motions of growing amplitude are not allowed in triply diffusive convection problem if M

 .

References

1. Brandt, A., Fernando H.J.S. (1996). Double Diffusive Convection .American Geophysical Union Washington, DC.
2. Stern, M .E. (1960). The Salt Fountain and Thermohaline Convection. Tellus. vol 12, 172.
3. Veronis, G. (1965) On Finite Amplitude Instability in Thermohaline Convection, J. Mar. Res. vol. 23, 1.
4. Banerjee, M. B.,Katoch D.C.,Dube G.S., Banerjee K. (1981) Bound for linear growth rate of a perturbation in Thermohaline Convection. Proc. Roy. Soc. London, Ser. AVol.378,301.
5. Gupta, J.R. Sood, S.K., Bhardwaj, U.D. (1986).On the characterization of nonoscillatory motions in rotatory hydromagnetic thermohaline convection. Indian J. Pure and Appl. Math. vol 17,100.
6. Mohan, H., Anjula. (2001). On the limitations of the linear growth rate in Veronis and Stern’s Thermohaline Convections. Indian J. Pure and Appl. Math. vol.32 (11), 1659- 1666.
7. Mohan, H. (2010). Bound for the Complex Growth Rate in Thermosolutal Convection Coupled with Cross-diffusion. Application and Applied Mathematics-An International Journal (AAM).vol. 5(10), 1428.
8. Griffiths, R.W. (1979).The Influence of a third Diffusing Component upon the onset of Convection. J. Fluid Mech. vol. 92,659.
9. Turner, J.S., Multicomponent Convection, Ann. Rev. Fluid Mech. 1985; 17:11-44p.
10. Pearlstein, A.J., Harris, R.M., Terrones (1989).The onset of Convective Instability in a Triply Diffusive Fluid Layer .J. Fluid Mech.vol .202, 443.
11. Lopez, A.R., Romero, L.A., Pearlstein, A.J. (1990).Effect of rigid boundaries on the onset of Convective Instability in a Triply Diffusive Fluid Layer. Physics of Fluids.vol.2 (6), 897.
12. Terrones, G. (1993). Cross-diffusion Effects on the Stability Criteria in a Triply- diffusive System. Phys. Fluids. vol.  A5. 2172.
13. Ryzhkov, I., I., Shevtsova, V.M. (2007). On Thermal Diffusion and Convection in Multicomonent Mixtures with Application to the Thermogravitational Column. Phys. Fluids. vol. 19, 1.
14. Ryzhkov, I., I., Shevtsova, V.M. (2009). Long Wave Instability of a Multicomponent Fluid Layer with the Soret Effect. Phys. Fluids. vol. 21. 1.
15. Rionero, S. (2013a).Triple Diffusive Convection in Porous Media.Act Mech.vol.224, 447.
16. Rionero, S. (2013b). Multicomponent Diffusive –Convective Fluid motions in Porous Layers ultimately boundedness, absence of subcritical Instability, and global nonlinear stability for any number of salts. Phys Fluids. vol. 25, 1.
17. Zhao, M., Wang, S., Zhang, Q. (2013). Onset of Triply Diffusive Convection in a Maxwell Fluid Saturated Porous Layer. Applied Mathematical Modelling. vol. 38, 2352.
18. Shivkumara, I.S., Kumar, S.B.N. (2013) Bifurcation in Triply Diffusive Couple Stress Fluid Systems. International Journal of Engineering Research and Applications. vol. 3 (6), 372.
19. Shivkumara, I.S., Kumar, S.B.N. (2014). Linear and Weakly Nonlinear Triple Diffusive Convection in a Couple Stress Fluid Layer. International Journal of Heat and Mass Transfer.vol.68, 542.
20. Schultz, M.H. (1973) Spline Analysis, Prentice-Hall, Englewood Cliffs, N.J.