International Journal of Mathematics and Computational Science, Vol. 1, No. 3, June 2015 Publish Date: May 16, 2015 Pages: 111-115
Fixed Point Theorems in Fuzzy Normed Spaces for Weak Contractive Mappings
S. A. M. Mohsenialhosseini*
Faculty of Mathematics, Vali-e-Asr University, Rafsanjan, Iran
Abstract
We define fixed point for the class of weak contractive type mappings in fuzzy normed spaces. We obtain several convergence theorems for fixed points by means of Picard iteration on fuzzy normed spaces. These extend the corresponding results in literature by providing error estimates, rate of convergence for the used iterative method as well as results concerning the data dependence of the fixed points on fuzzy norm spaces.
Keywords
Fuzzy Normed Space, Fuzzy Fixed Point, Weak Contraction, Convergence Theorem
Received: April 6, 2015 / Accepted: April 22, 2015 / Published online: May 11, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
Nowadays, fixed point play an important role in different areas of mathematics, and its applications, particularly in mathematics, physics, differential equation. For details, one can refer to, Amann, [1] Franklin, [2] Mohsenalhosseini et al. [3]. Since fuzzy mathematics and fuzzy physics along with the classical ones are constantly developing, the fuzzy type of the fixed point can also play an important role in the new fuzzy area. Some mathematicians have defined fuzzy norms on a vector space from various points of view [4], [5].
Chitra and Mordeson [6] introduce a definition of norm fuzzy and thereafter the concept of fuzzy norm space has been introduced and generalized in different ways by Bag and Samanta in [7], [8], [9].
In this paper, starting from the article of Berinde [10], we study some well-known contractive type mappings on fuzzy normed spaces, and we give some fuzzy approximate fixed points of such mappings.
2. Some Preliminary Results
Throughout this article, the symbols ∧ and ∨ mean the min and the max, respectively. We now start our work with the following:
Definition 2.1. [7] Let U be a linear space on 
A function 
is called fuzzy norm if and only if for every 
and for every 
the following properties are satisfied:
(F1) : 
for every 
,
(F2) : 
if and only if 
for every 
,
(F3) : 
for every 
and ,
(F4) : 
for every
,
(F5) : the function 
is nondecreasing on 
and 
.
(F6) : 
(F7) : The function 
is continuous for every 
, and on subset 
is strictly increasing.
Let 
be a fuzzy norm space. For all 
we define 
-norm on 
as follows:
(1)
for every 
Definition 2.2. [11] Let 
be a fuzzy normed space, 
and 
The 
is a 
-approximate fixed point (fuzzy approximate fixed point) of 
if for some 
Definition 2.3. [11] A mapping is a F-Kannan operator if there exists 
such that
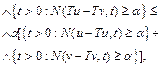
for all 
3. Fuzzy Fixed Point
Definition 3.1. A mapping is called -weak contraction or 
-contraction if there exist a constant 
and some 
such that
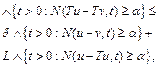(2)
for all
Remark 3.2. Due to the symmetry of the distance, the weak contraction condition (2) implicitly includes the following dual one
(3)
for all
Remark 3.3. In the rest of the paper we will denote the set of all -fixed points of 
by
(4)
for some 
Proposition 3.4. Let be a fuzzy normed space and is an -weak contraction. Then
1) 
2) The Picard iteration 
given by
converges to 
for any
3) The following estimates
A)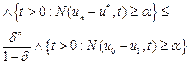 
(5)
for 
B) 
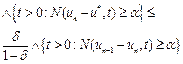(6)
for 
hold, where is constant.
Proof: Let be the Picard iteration, starting from arbitrary. Then by (2) we have
By the Picard iteration of , we have
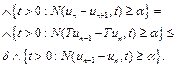
By induction
and hence
which yields
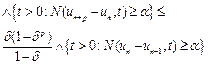(7)
all
Since,
from (7) we obtain
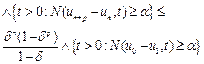(8)
Now by letting 
in (8) and (7) we obtain the estimates (5) and (6), respectively.
Proposition 3.5. Let be a fuzzy normed space and is an -weak contraction for which there exist 
and some 
such that
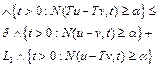(9)
for all Then
1) 
has a unique -fixed point, i.e. 
2) The Picard iteration given by
converges to for any
3) The a priori and a posteriori error estimates
A)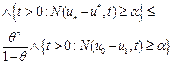 
(10)
for
B)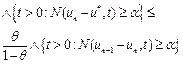 
(11)
for
hold.
4) The rate of convergence of the Picard iteration is given by
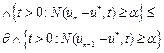(12)
Proof: Let be the Picard iteration, starting from arbitrary. Then by (2) we have
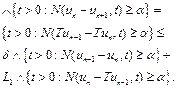
By the Picard iteration of , we have
By induction
and hence
which yields
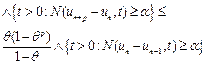(13)
for all Since,
from (13) we obtain
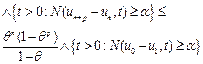(14)
Now by letting in (14) and (13) we obtain the estimates (10) and (11), respectively.
Again, by (2) we have
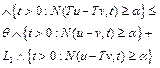(15)
where 
,
.
Take 
in (15) to obtain
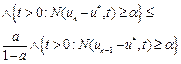
that is, the estimate (12).
Remark 3.6.Note that, by the symmetry of the distance, (9) is satisfied for all 
if and only if
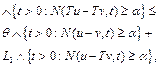(16)
also holds, for all
Corollary 3.7. Let be a fuzzy normed space and is an F-Kannan operator Then
1) has a unique -fixed point, i.e.
2) The Picard iteration given by
converges to for any
3) The a priori and a posteriori error estimates
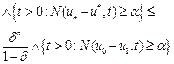
for
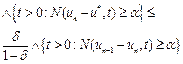
for
hold.
4) The rate of convergence of the Picard iteration is given by
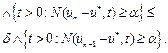
Proof: By Definition 2.3. and triangle rule, we get
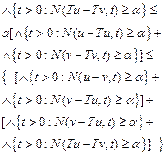
Therefore
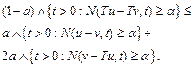
Then
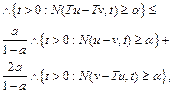
for all 
i.e., in view of 
Definition 3.1. holds with 
,
.
Since F-Kannan operator is symmetric with respect to 
and
(3) also holds. In a similar way, by the same Definition 2.3. and triangle rule, we get
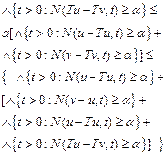
Therefore
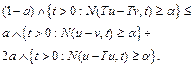
Then
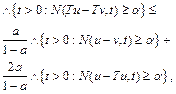
for all which shows that (9) and (16) hold with ,.
Acknowledgments
The authors are extremely grateful to the referees for their helpful suggestions for the improvement of the paper.
References
- H. Amann, Fixed point equations and nonlinear eigenvalue problems inor4'ed Banach spaces, SIAM Rev., 18(2) (1976), 620-709.
- J. Franklin, Methods of Mathematical Economics, Springer Verlag, NewYork, (1980).
- S.A.M. Mohsenalhosseini, H. Mazaheri, M.A. Dehghanand M. Bagheshahi,"Application of Approximate Best Proximity Pairs," Gen. Math. Notes, Vol. 7, No. 1, pp.59-65, 2011.
- S. V. Krishna and K. K.M. Sarma, "Separation of fuzzy normed linear spaces," Fuzzy Sets and Systems, vol. 63, no. 2, pp. 207-217, 1994.
- J.-z. Xiao and X.-h. Zhu, "Fuzzy normed space of operators and its completeness," Fuzzy Sets and Systems, vol. 133, no. 3, pp. 389–399, 2003.
- A. Chitra, P.V., "Mordeson, "Fuzzy linear operators and fuzzy normed linear spaces,"Bull. Cal. Math.Soc, vol. 74, pp. 660-665, 1969.
- T. Bag, S. K. Samanta, "Finite dimensional fuzzy normed linear spaces,"J. Fuzzy Math, vol. 11, no. 3, pp. 687-705, 2003.
- T. Bag, S. K. Samanta, "Fuzzy bounded linear opera- tors,"Fuzzy Sets syst, vol. 151, no. 3, pp. 513-547, 2005.
- T. Bag, S. K. Samanta, "Some fixed point theorems in fuzzy normed linear spaces," Information Sciences, 177 pp. 3271-3289, 2007.
- V. Berinde, "On the Approximation of Fixed Points of Weak Contractive Mappings," Carpathian J. Math, vol 19, no. 1, pp. 7-22, 2003.
- S. A. M. Mohsenalhosseini1 and H.Mazaheri, " Approx- imate Fixed Point Theorems in Fuzzy normed Spaces s for an Operator," Advances in Fuzzy Systems, Volume 2013, Article ID 613604, 8 pages.
