New Efficient Optimal Derivative-Free Method for Solving Nonlinear Equations
Q. W. Guo, Y. H. Qian*
Department of Mathematics, Zhejiang Normal University, Jinhua, Zhejiang, China
Abstract
In this paper, we suggest a new technique which uses Lagrange polynomials to get derivative-free iterative methods for solving nonlinear equations. With the use of the proposed technique and Steffens on-like methods, a new optimal fourth-order method is derived. By using three-degree Lagrange polynomials with other two-step methods which are efficient optimal methods, eighth-order methods can be achieved. Besides, we can get sixteenth-order methods if we use other three-step methods and higher-order degree Lagrange polynomials. The error equations and asymptotic convergence constants are obtained for the proposed methods. Some numerical examples are illustrated to verify the accuracy of the proposed computational scheme.
Keywords
Lagrange Polynomials, Steffens on-Like Method, Derivative-Free, Convergence Order, Efficiency Index
Received: March 27, 2015 / Accepted: April 16, 2015 / Published online: May 8, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
One of the most basic and complex problems in numerical analysis is to solve nonlinear equations in terms of ![]() . However, it is somewhat difficult to find the roots of nonlinear equations accurately. Iterative methods are the most commonly used techniques to obtain approximate solutions.
. However, it is somewhat difficult to find the roots of nonlinear equations accurately. Iterative methods are the most commonly used techniques to obtain approximate solutions.
Let ![]() be a root of the equation
be a root of the equation
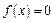 . (1)
. (1)
We change the equation (1) as equivalent form
![]() . (2)
. (2)
Taking![]() , construct the recursive formula
, construct the recursive formula
![]() . (3)
. (3)
We get a sequence ![]() through the recursive formula (3). Taking limit on both sides of the formula (3), we can get
through the recursive formula (3). Taking limit on both sides of the formula (3), we can get
![]() , (4)
, (4)
where![]() is a limit of the sequence
is a limit of the sequence![]() when
when ![]() . Obviously,
. Obviously, ![]() is a root of the equation (2) through the formula (4). Because of equation (1) is equal to (2), we would obtain
is a root of the equation (2) through the formula (4). Because of equation (1) is equal to (2), we would obtain
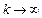
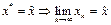 , (5)
, (5)
and the equation (3) is called iterative formula. Meanwhile, the method using equation (3) is named iterative method.
Newton’s method [1] is the classical approach for solving nonlinear equations, the computational algorithm is written as follows:
![]() . (6)
. (6)
where![]() . This is an example of a one-point iteration scheme [10]. In some applications,
. This is an example of a one-point iteration scheme [10]. In some applications, ![]() is more difficult to evaluate than
is more difficult to evaluate than![]() . Recently, much research effort [7, 9, 17, 20,21] enlightened the ideas of removing derivatives from iteration functions in order to avoid the necessity of defining new function evaluations, such as the first derivative or second derivative. For example, Steffensen [12] made use of the forward difference approximation to replace
. Recently, much research effort [7, 9, 17, 20,21] enlightened the ideas of removing derivatives from iteration functions in order to avoid the necessity of defining new function evaluations, such as the first derivative or second derivative. For example, Steffensen [12] made use of the forward difference approximation to replace![]() to propose the following computational scheme
to propose the following computational scheme
![]() . (7)
. (7)
Recently, Dehghan and Hajarian [6] presented a third order iterative method (DM) and incorporated four function evaluations per each iteration step as follows
![]() , (8)
, (8)
where ![]() . Besides, Ren et al. [15] proposed another optimal fourth-order method in terms of the following scheme (RMa,
. Besides, Ren et al. [15] proposed another optimal fourth-order method in terms of the following scheme (RMa, ![]() , and ‘a’ is a parameter).
, and ‘a’ is a parameter).
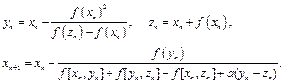 (9)
(9)
In Eq. (9), the function![]() is represented by
is represented by![]() . Afterward, Liu et al. [11] presented a fourth-order method (LM) as follows
. Afterward, Liu et al. [11] presented a fourth-order method (LM) as follows
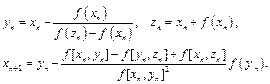 (10)
(10)
The aforementioned methods [6, 11, 15] are optimal in accordance with Kung-Traub conjecture to obtain a derivative-free computational scheme.
It is not limited to the above computational scheme [6, 11, 15], many variants of Steffensen’s methods were proposed in the past decade. Sharma [16] introduced a Newton-Steffensen method to achieve the third order convergence. Cordero et al. [4] proposed a new fourth-order Steffensen type method. In addition, other researchers also introduced a variety of new methods to solve nonlinear equations based on Steffensen’s type method (see the literature published in [3, 14, 15, 18]). Meanwhile, there are various methods using linear functions to calculate![]() . For example, Gustavo et al. in [8] presented three new optimal fourth-order methods to consider the polynomial. Cordero et al. [5] and Soleymani [19] proposed Padé approximants to estimate
. For example, Gustavo et al. in [8] presented three new optimal fourth-order methods to consider the polynomial. Cordero et al. [5] and Soleymani [19] proposed Padé approximants to estimate![]() .
.
In this paper, a new optimal technique is presented to adopt Lagrange’s interpolation and Steffensen-like methods to exclude derivative functions in the computational iteration scheme. The paper is organized as follows, the methodology and principle of the new optimal technique, using Lagrange’s interpolation, for solving nonlinear equations is introduced in Section 2. In the next section, the proposed technique is generalized for getting eighth-order methods which are both derivative-free and optimal. In Section 4, we can derive the sixteenth-order methods when the proposed technique and other three-step optimal methods are used. Illustrative examples are given to verify the accuracy of the proposed method in Section 5. Finally, the paper ends with concluding remarks in Section 6.
2. Fourth-Order Optimal Method
We consider a general nonlinear equation![]() . Assuming that
. Assuming that ![]() is a simple root of the equation
is a simple root of the equation ![]() , and
, and ![]() is a given initial guess which is close enough to
is a given initial guess which is close enough to ![]() . According to Taylor’s series expansion around
. According to Taylor’s series expansion around ![]() gives
gives
![]() (11)
(11)
The first-order approximating equation is
![]() . (12)
. (12)
Then from Eq. (12), we can infer the following iterative method
![]() . (13)
. (13)
This is the classical Newton’s method with a second-order convergence. Using the following forward-difference to replace ![]() yields
yields
![]() . (14)
. (14)
We can get Steffensen’s method by making use of Eq. (14). Then we obtain a method formed by the composition of Steffensen and Newton methods as follows:
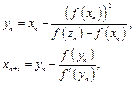 (15)
(15)
Where ![]() ,this uses four function evaluations which are
,this uses four function evaluations which are ![]() ,
,![]() ,
,![]() ,
,![]() . In order to avoid the evaluation of the first derivative and reduce the function evaluations, it is suggested approximating it by the derivative
. In order to avoid the evaluation of the first derivative and reduce the function evaluations, it is suggested approximating it by the derivative![]() of the following Lagrange polynomial of degree 2.
of the following Lagrange polynomial of degree 2.
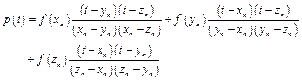 (16)
(16)
Then the derivative of ![]() evaluated in
evaluated in![]() can be expressed as
can be expressed as
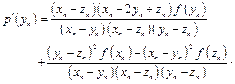 (17)
(17)
Substituting Eq. (17) in the second equation of Eq. (15), we get a new two-step iterative method (GM) using the Lagrange polynomial whose expression is written as follows:
![]() (18)
(18)
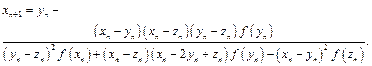
Theorem 2.1. Let ![]() be a simple zero of a sufficiently differentiable function
be a simple zero of a sufficiently differentiable function![]() :
: ![]() in an interval
in an interval![]() . If
. If ![]() is sufficiently close to
is sufficiently close to ![]() ,then the method (18) has optimal fourth-order convergence.
,then the method (18) has optimal fourth-order convergence.
![]() Let
Let ![]() be the error in
be the error in![]() , which is
, which is ![]() . By Taylor expanding at
. By Taylor expanding at ![]() , we have
, we have
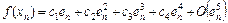 , (19)
, (19)
where ![]() .
.
On the basis of ![]() , we get
, we get
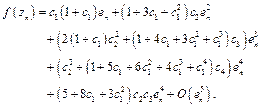 (20)
(20)
Substituting Eq. (19) and (20) in the first equation of Eq. (18), we have
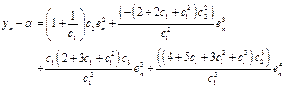
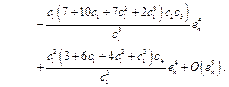 (21)
(21)
Then, we get
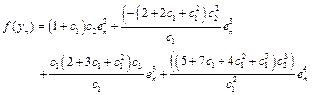
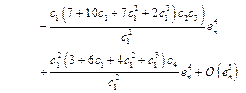 (22)
(22)
with Eq. (19), (20) and (22), we can deduce that the error equation of the GM method is
![]() (23)
(23)
showing that the method (GM) has optimal fourth-order convergence.
3. Eighth-Order Optimal Methods
The technique can be further applied to higher order methods by using higher degree Lagrange polynomials. To obtain derivative-free methods having optimal eighth-order convergence, we consider a three-step cycle in which the first two steps are any derivative-free optimal fourth-order methods, and![]() is a function that defines an optimal derivative free method for
is a function that defines an optimal derivative free method for![]() , the combination of
, the combination of![]() and
and![]() defines an optimal derivative-free iterative method for
defines an optimal derivative-free iterative method for ![]() ,
,
![]() .
.
Then, the derivative![]() of the following Lagrange polynomial of degree 3 is used to replace
of the following Lagrange polynomial of degree 3 is used to replace![]() .
.
According to the Lagrange polynomial, we get
 (25)
(25)
Then the derivative of ![]() evaluated in
evaluated in ![]() can be expressed as
can be expressed as
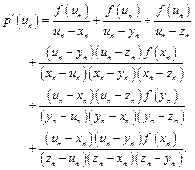 (26)
(26)
Using ![]() to replace
to replace![]() obtains the following three-step class
obtains the following three-step class
![]() (27)
(27)
![]() ,
,
where ![]() is the derivative of
is the derivative of![]() in
in![]() , in other words,
, in other words, ![]() =
=![]() . We evaluate four functions which are
. We evaluate four functions which are![]() ,
,![]() ,
,![]() ,
,![]() in each iteration. The computational method stated in Eq. (27) will be optimal if we prove that it has eighth-order convergence.
in each iteration. The computational method stated in Eq. (27) will be optimal if we prove that it has eighth-order convergence.
Theorem 3.2. Let ![]() be a simple zero of a sufficiently differentiable function
be a simple zero of a sufficiently differentiable function![]() :
: ![]() in an interval
in an interval![]() . If
. If ![]() is sufficiently close to
is sufficiently close to ![]() ,then the method (27) has optimal eighth-order convergence.
,then the method (27) has optimal eighth-order convergence.
![]() Let
Let ![]() . By Taylor expanding at
. By Taylor expanding at![]() , we have
, we have
 , (28)
, (28)
where ![]() .
.
On the basis of![]() , we obtain
, we obtain
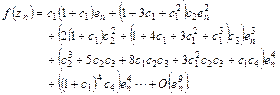 (29)
(29)
Substituting Eq. (28) and (29) in the first equation of Eq. (27), we have

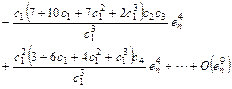 (30)
(30)
Then, we expand![]() around
around![]() with Eq. (30) to derive the following expression.
with Eq. (30) to derive the following expression.

 (31)
(31)
We define that the first two steps are optimal fourth-order method, and assume
 , (32)
, (32)
with Eq. (28), (29) and (31), we can thus deduce the error equation of the method as
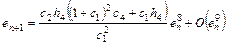 . (33)
. (33)
The above method shows the optimal eighth-order convergence.
For example, applying RM1 (assume ![]() ) in (27), we get the method (GRM):
) in (27), we get the method (GRM):
![]() (34)
(34)

The above calculation method satisfies the following error equation:
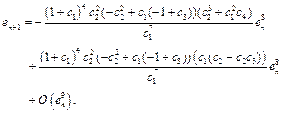 (35)
(35)
In addition, if we apply the method of LM in Eq. (27), we can get another method (GLM) in the form of:
![]()
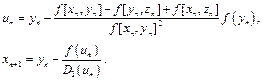 (36)
(36)
This method satisfies the following error equation:
![]()
![]() (37)
(37)
4. Sixteenth-Order Optimal Methods
To further obtain derivative-free methods of optimal sixteenth-order convergence, we consider a four-step cycle in which the first three steps are any derivative-free optimal eighth-order method as follows:
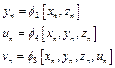
![]() . (38)
. (38)
Where ![]() is a iterative function of optimal eighth order derivative-free method composed with
is a iterative function of optimal eighth order derivative-free method composed with ![]() ,
,![]() . The derivative
. The derivative![]() of the following Lagrange polynomial of degree 4 is adopted to replace
of the following Lagrange polynomial of degree 4 is adopted to replace ![]() .
.
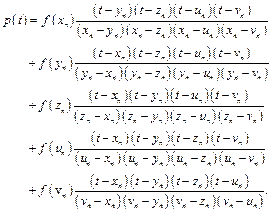 (39)
(39)
Then the derivative of![]() evaluated in
evaluated in![]() can be expressed as
can be expressed as
 (40)
(40)
Using ![]() replaces
replaces ![]() , we get the following three-step class
, we get the following three-step class
 (41)
(41)
![]() ,
,
where ![]() is the derivative of
is the derivative of ![]() in
in ![]() , in otherwords,
, in otherwords,![]() =
=![]() .We evaluate five functions in each iteration. The method will be optimal if we prove that it has sixteenth-order convergence.
.We evaluate five functions in each iteration. The method will be optimal if we prove that it has sixteenth-order convergence.
Theorem 4.2. Let ![]() be a simple zero of a sufficiently differentiable function
be a simple zero of a sufficiently differentiable function![]() :
: ![]() in an interval
in an interval![]() . If
. If ![]() is sufficiently close to
is sufficiently close to ![]() , then the method (41) has optimal sixteenth-order convergence.
, then the method (41) has optimal sixteenth-order convergence.
![]() Let
Let ![]() . By Taylor expanding at
. By Taylor expanding at![]() , we have
, we have
 , (42)
, (42)
where ![]() .
.
On the basis of ![]() , we obtain
, we obtain
 (43)
(43)
Substituting Eq. (42) and (43) in the first equation of Eq. (41), we have

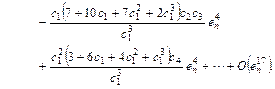 (44)
(44)
Then, we expand ![]() around
around ![]() with Eq. (44) to achieve the following equation.
with Eq. (44) to achieve the following equation.
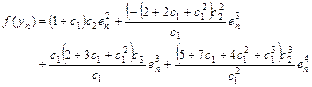
 (45)
(45)
We define that the first three steps are optimal eighth-order method, we thus get
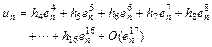 , (46)
, (46)
![]() (47)
(47)
Finally, the error equation of the method can be derived as follows:
![]() (48)
(48)
The above equation shows that the method (41) has an optimal fourth-order convergence.
5. Numerical Examples
The proposed methods described in Section 4 using the new technique are employed to solve some illustrative nonlinear problems. The obtained results are compared with Steffensen’s method (SM, (7)), Dehghan and Hajarian’s method (DM, (8)). Using Lagrange polynomials, we get a new optimal fourth-order method (GM) and two new optimal eighth-order methods (GRM, GLM).
All the computations were conducted by using MATLAB 8.0, we selected an approximate solution rather than the exact root computed with 1500 digits. The stopping criterion used is![]() , the iterative succession convergence was checked to verify the accuracy of the approximate solutions. Table 2 shows the number of the iterations needed to reach the acceptable tolerance for each method and estimates the computational order of convergence
, the iterative succession convergence was checked to verify the accuracy of the approximate solutions. Table 2 shows the number of the iterations needed to reach the acceptable tolerance for each method and estimates the computational order of convergence ![]() (usually called ACOC), defined by Cordero and Torregrosa [2] :
(usually called ACOC), defined by Cordero and Torregrosa [2] :
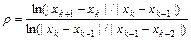 . (49)
. (49)
In Table 1, we show the comparison of efficiency indices [13] for different methods of various orders. The efficiency indices is defined as ![]() , where
, where ![]() is the order of convergence,
is the order of convergence, ![]() is the number of function evaluations per step.
is the number of function evaluations per step.
We use the following functions in numerical comparison:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
It is found that the efficiency index of the methods (GM, GRM, GLM) are better than other methods from Table 1. From Table 2, we can find that the method (GM) converges more rapidly than Steffensen’s method, Dehghan and Hajarian’s method. The eighth-order methods (GRM, GLM) require less iterative steps to reach the stopping criterion. All theoretical order of convergence.
Table 1. Orderder and efficiency indices of some methods
| Methods | SM | DM | GM | GRM | GLM |
| Order | 2 | 3 | 4 | 8 | 8 |
| Efficiency index |
|
|
| 2 | 2 |
Table 2. Numerical results for nonlinear equation.
| SM | DM | GM | GRM | GLM | |||||||
| Iter | Error | Iter | Error | Iter | Error | Iter | Error | Iter | Error | ||
|
| 0.2 | 1 | 5.83e-2 | 1 | 5.72e-2 | 1 | 5.75e-2 | 1 | 5.75e-2 | 1 | 5.75e-2 |
| 2 | 8.15e-4 | 2 | 2.77e-4 | 2 | 3.85e-7 | 2 | 7.99e-13 | 2 | 6.00e-14 | ||
| 3 | 1.73e-7 | 3 | 3.26e-11 | 3 | 7.64e-28 | 3 | 1.18e-99 | 3 | 8.60e-110 | ||
|
|
| 4 | 5.32e-32 | 4 | 1.19e-110 | 4 | 2.71e-794 | 4 | 1.53e-876 | ||
| 7 | 1.04e-117 | 5 | 1.89e-281 | 5 | 6.94e-442 | ||||||
| 8 | 2.80e-235 | ||||||||||
|
| 2.00004 | 3.00000 | 4.00005 | 7.99993 | 8.00001 | ||||||
|
| 1.5 | 1 | 2.48e-1 | 1 | 2.47e-1 | 1 | 2.46e-1 | 1 | 2.46e-1 | 1 | 2.46e-1 |
| 2 | 1.46e-2 | 2 | 1.27e-3 | 2 | 2.27e-6 | 2 | 2.17e-11 | 2 | 1.45e-13 | ||
| 3 | 5.12e-8 | 3 | 3.26e-11 | 3 | 1.41e-26 | 3 | 5.54e-92 | 3 | 4.40e-114 | ||
|
|
| 4 | 1.20e-32 | 4 | 2.11e-107 | 4 | 1.01e-736 | 4 | 1.01e-736 | ||
| 7 | 1.09e-141 | 5 | 6.01e-98 | 5 | 1.04e-430 | ||||||
| 8 | 2.86e-284 | 6 | 7.53e-294 | ||||||||
|
| 1.99993 | 3.00002 | 4.00009 | 7.99995 | 8.00002 | ||||||
|
| 4.15 | 1 | 1.53e-1 | 1 | 2.59e-3 | 1 | 1.53e-1 | 1 | 2.59e-3 | 1 | 2.59e-3 |
| 2 | 5.88e-4 | 2 | 2.73e-10 | 2 | 5.86e-8 | 2 | 3.03e-26 | 2 | 6.65e-30 | ||
| 3 | 8.30e-9 | 3 | 3.20e-31 | 3 | 1.15e-33 | 3 | 1.05e-209 | 3 | 1.25e-242 | ||
|
|
| 4 | 5.16e-94 | 4 | 1.71e-136 | ||||||
| 7 | 2.55e-154 | 5 | 2.15e-282 | 5 | 8.33e-548 | ||||||
| 8 | 1.56e-309 | ||||||||||
|
| 2.00001 | 3.00004 | 4.00002 | 8.00024 | 8.00008 | ||||||
|
| -0.5 | 1 | 6.33e-2 | 1 | 5.68e-2 | 1 | 5.72e-2 | 1 | 5.71e-2 | 1 | 5.71e-2 |
| 2 | 6.12e-3 | 2 | 3.44e-4 | 2 | 9.87e-6 | 2 | 1.68e-9 | 2 | 3.93e-10 | ||
| 3 | 7.02e-5 | 3 | 8.06e-11 | 3 | 8.61e-21 | 3 | 7.71e-70 | 3 | 1.72e-75 | ||
|
|
| 4 | 1.04e-30 | 4 | 4.99e-81 | 4 | 1.51e-551 | 4 | 2.29e-598 | ||
| 8 | 1.90e-125 | 5 | 2.20e-90 | 5 | 5.63e-322 | ||||||
| 9 | 6.63e-250 | 6 | 2.09e-269 | ||||||||
|
| 1.99998 | 2.99997 | 4.00000 | 8.00003 | 8.00007 | ||||||
|
| 2.5 | 1 | 6.08e-2 | 1 | 4.34e-2 | 1 | 3.19e-1 | 1 | 3.45e-1 | 1 | 3.45e-1 |
| 2 | 6.33e-2 | 2 | 5.35e-2 | 2 | 2.70e-2 | 2 | 4.65e-4 | 2 | 3.44e-4 | ||
| 3 | 6.45e-2 | 3 | 6.74e-2 | 3 | 6.39e-6 | 3 | 4.98e-25 | 3 | 2.42e-26 | ||
|
|
|
|
|
|
| 4 | 8.76e-193 | 4 | 1.45e-203 | ||
| 14 | 9.47e-149 | 10 | 6.90e-76 | 5 | 5.62e-78 | ||||||
| 15 | 6.21e-296 | 11 | 9.24e-225 | 6 | 1.48e-308 | ||||||
|
| 2.00000 | 3.00000 | 4.00000 | 7.99983 | 7.99989 | ||||||
|
| 1.5 | 1 | 1.08e-1 | 1 | 9.43e-2 | 1 | 9.54e-2 | 1 | 9.55e-2 | 1 | 9.55e-2 |
| 2 | 1.22e-2 | 2 | 1.17e-3 | 2 | 1.03e-4 | 2 | 1.44e-10 | 2 | 8.99e-11 | ||
| 3 | 1.75e-4 | 3 | 3.38e-9 | 3 | 1.01e-16 | 3 | 2.07e-81 | 3 | 5.53e-83 | ||
|
|
|
|
| 4 | 9.01e-65 | 4 | 3.69e-648 | 4 | 1.13e-660 | ||
| 8 | 6.63e-119 | 5 | 1.20e-75 | 5 | 7.42e-257 | ||||||
| 9 | 5.10e-237 | 6 | 3.72e-225 | ||||||||
|
| 2.00000 | 3.00000 | 4.00000 | 8.00000 | 7.99999 | ||||||
|
| 1.5 | 1 | 5.33e-2 | 1 | 7.82e-2 | 1 | 1.32e-1 | 1 | 1.35e-1 | 1 | 1.35e-1 |
| 2 | 4.45e-2 | 2 | 5.09e-2 | 2 | 2.50e-3 | 2 | 4.61e-6 | 2 | 3.25e-6 | ||
| 3 | 2.75e-2 | 3 | 5.65e-3 | 3 | 1.02e-9 | 3 | 1.32e-40 | 3 | 5.20e-42 | ||
|
|
|
|
| 4 | 2.98e-35 | 4 | 5.94e-317 | 4 | 2.21e-328 | ||
| 11 | 1.08e-142 | 7 | 8.43e-122 | 5 | 2.14e-137 | ||||||
| 12 | 1.00e-283 | 8 | 2.00e-362 | 6 | 5.64e-546 | ||||||
|
| 2.00000 | 3.00000 | 4.00000 | 8.00000 | 7.99999 | ||||||
|
| 1.2 | 1 | 2.16e-1 | 1 | 2.15e-1 | 1 | 2.15e-1 | 1 | 2.15e-1 | 1 | 2.15e-1 |
| 2 | 1.06e-3 | 2 | 8.24e-5 | 2 | 6.15e-7 | 2 | 2.61e-12 | 2 | 1.93e-13 | ||
| 3 | 2.56e-8 | 3 | 2.12e-14 | 3 | 4.47e-29 | 3 | 1.19e-99 | 3 | 7.39e-110 | ||
|
|
| 4 | 3.59e-43 | 4 | 1.25e-117 | 4 | 2.27e-798 | 4 | 3.36e-881 | ||
| 7 | 8.10e-147 | 5 | 1.75e-129 | 5 | 7.63e-472 | ||||||
| 8 | 1.50e-294 | 6 | 2.03e-388 | ||||||||
|
| 2.00000 | 3.00000 | 4.00000 | 8.00000 | 8.00000 |
6. Conclusions
We proposed a new derivative-free fourth-order method (GM) which is optimal order of convergence in the sense of Kung-Traub conjecture. Making use of the new technique, we obtain other two eighth-order methods which are an optimal method without derivative functions. Higher order methods can also be constructed using the proposed method, such as sixteenth-order methods. The convergence of the method is proved in the paper. Illustrative numerical examples are shown in this paper to demonstrate the efficiency of the new methods in terms of its efficiency of index and computational efficiency index. The proposed methods are capable of solving various nonlinear equations and can achieve good convergence.
Acknowledgements
The author Y.H. Qian gratefully acknowledge the support of the National Natural Science Foundations of China (NNSFC) through grant No. 11202189, and the financial support of China Scholarship Council (CSC) through grant No. 201408330049. The author Q.W. Guo gratefully acknowledge the support of the National Training Programs of Innovation and Entrepreneurship for Undergraduates. The authors wish to acknowledge the valuable participation of Dr. S.K. Lai in the proof-reading of this paper.
References
[1] Argyros, I. K.: Convergence and Application of Newton-Type Iterations. Spriner, New York, 2008.
[2] Cordero, A., Torregrosa, J.R.: Variants of Newton’s method using fifth-order quadrature formulas. Appl.Math. Comput. 190 (1), 686-698, 2007.
[3] Cordero, A., Torregrosa, J.R.: A class of Steffensen type methods with optimal order of convergence. Appl. Math. Comput. 217(19), 7653-7659, 2011.
[4] Cordero, A., Hueso, J. L., Martínez, E., Torregrosa, J. R.: Steffensen type methods for solving non-linear equations. J. Comput. Appl. Math. 236(12), 3058-3064 (2012).
[5] Cordero, A., Hueso, J. L., Martínez, E., Torregrosa, J.R.: A new technique to obtain derivative-free optimal iterative methods for solving nonlinear equations. J. Comput. Appl. Math. 252, 95-102, 2013.
[6] Dehghan, M., Hajarian, M.: Some derivative free quadratic and cubic convergence iterative formulas for solving nonlinear equations. J. Comput. Appl. Math. 29(1), 19-30, 2010.
[7] Echebest, N., Schuverdt, M. L., Vignau, R. P.: Two derivative-free methods for solving underdetermined nonlinear systems of equations. Comput. Appl. Math. 30(1), 217-245, 2011.
[8] Fernandez-Torres,G., Vasquez-Aquino, J.: Three New Optimal Fourth-Order Iteaive Methods to Solve Nonlinear Equations. Adv. Numer. Anal.2013,Article ID957496, 2013.
[9] Fernandez-Torres,G.: Derivative free iterative methods with memory of arbitraryhigh convergence order. Numer Algor. 67, 565-580, 2014.
[10] Kung, H.T., Traub, J.F.: Optimal order of one-point and multi-point iteration. J. Assoc. Comput. Math. 21, 643-651, 1974.
[11] Liu, Z.L., Zheng, Q., Zhao, P.: A variant of Steffensen’s method of fourth-order convergence and its applications. Appl. Math. Comput. 216, 1978-1983, 2010.
[12] Ortega, J.M., Rheinboldt, W.G.: Iterative Solutions of Nonlinear Equations in Several Variables. Academic Press, New York, 1970.
[13] Ostrowski, A.M.: Solutions of Equations and Systems of Equations. Academic
[14] Păvăloiu, I., Cătinaş, E.: On a Newton-Steffensen type method. Appl. Math. Lett. 26(6), 659-663, 2013.
[15] Ren, H.M., Wu, Q.B., Bi, W.H.: A class of two-step Steffensen type methods with fourth-order convergence. Appl. Math. Comput. 209(2), 206-210, 2009.
[16] Sharma, J.R.: A composite third order Newton-Steffensen method for solving nonlinea equations. Appl. Math. Comput. 169(1), 242-246, 2005.
[17] Sharma, J.R., Arora, H.: An efficient derivative free iterative method for solving systems of nonlinear equations. Appl. Anal. Discrete Math. 7, 390-403, 2013.
[18] Soleymani, F., Karimi Vanani, S.: Optimal Steffensen-type methods with eighth order of convergence. Comput. Math. Appl. 62(12), 4619-4626, 2011.
[19] Soleymani, F., Karimi Vanani, S., Jamali Paghaleh, M.: A class of three-step derivative-free root solvers with optimal convergence order. J. Appl. Math. 2012, Article ID 568740, 2012.
[20] Thukral, R.: New Higher Order Derivative-Free Methods for Solving Nonlinear Equations. J. Numer. Math. Stoch. 4(1), 59-69, 2012.
[21] Wang, H., Li, S.B.: A family of derivative-free methods for nonlinear equation.Rev. Mat. Complut. 24, 375-389, 2011.



