Study of Multilayer Flow of Viscous Incompressible Fluid and Application of Its Results for Capillary Blood Flow Simulation

N. Khomasuridze, N. Zirakashvili^*

I. Vekua Institute of Applied Mathematics of Iv. Javakhishvili Tbilisi State University, 2 University St., Tbilisi, Georgia

Abstract

Linear stationary multilayer flows of a viscous incompressible fluid in tubes bounded by coordinate surfaces of generalized cylindrical coordinates and circular flows of multilayer liquids in a circular cylindrical system of coordinates are investigated. In other words, multilayer flows are studied in rectilinear tubes of rectangular, circular, elliptic and parabolic cross-sections and in circular tubes of rectangular cross-section. Layers of flowing fluids of different viscosity are arranged along one of the coordinates. Related boundary-value contact problems of hydromechanics are stated and their effective solutions are found. The obtained results are used in studies of blood microcirculation.

Keywords

Viscous Incompressible Fluid, Boundary-Value Contact Problem, Fourier Trigonometric Series

Received: March 15, 2015
Accepted: April 2, 2015
Published online: April 6, 2015

@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/

1. Introduction

There are a number of papers studying flows of viscous incompressible fluids in tubes of circular cross-section. A much lesser number of works deal with flows of fluids in tubes of more complex sections and only a few works consider multilayer flows in rectilinear and circular tubes of various cross-section.

In the present paper we consider stationary multilayer flows of a viscous incompressible fluid in tubes bounded by coordinate surfaces of generalized cylindrical coordinates, in particular coordinate surfaces of Cartesian, circular-cylindrical, elliptic-cylindrical, parabolic-cylindrical and bipolar-cylindrical coordinate systems [1], [2]. In a circular-cylindrical system of coordinates multilayer flows of a fluid in circular tubes of rectangular cross-section are considered. Naturally, layers flowing in the tubes are assumed to have different viscosity.

The results obtained in this work can be used in studies of blood microcirculation, mudflows, etc.

The effectiveness of our approach is demonstrated by an example describing blood flows along narrow vessels with lumen (the diameter) of 15-80mμ. But first we must give a short review of works dealing with microcirculation of blood along vessels with the above-given lumen (diameter) of the vessels.

The main resistance to the blood flow in the organism is observed in the microcirculatory bed – very fine capillaries, arterioles and venous [3], [4], with lumen varying from 15 mm to 80 mm. The determinant parameters of blood flow are viscosity of the medium consisting of plasma and erythrocyte flows and erythrocyte flow density in the vessels. The rheological properties of the blood depend on the velocity of the displacement, the radii and geometry of the vessels in which the blood flows [3], [4], [5]. For micro vessels the term "viscosity" is ambivalent since blood is represented by a single flow of plasma and erythrocytes and therefore the term "seeming viscosity" is frequently used [5].

Before we continue our discussion we should highlight the following two theses characterizing blood circulation.

Erythrocytes tend to gather into a rapid axial stream, while plasma flows more slowly in layers adjoining vessel walls. The nature of physical forces that make erythrocytes drift to the axis is little studied.

Although some researchers believe that blood flows in fine arterioles and venous do not have the property of the Newtonian fluid [6], [7], but the low velocity of displacement and small values of the Reynolds number make it possible  to model the flow by  Navier-Stokes equations.

In [8] and [9], the flow of erythrocytes in small capillaries is considered as a flow of individual rigid globules in the plasma. However for arterioles and venous of a diameter varying from 15 mm to 80 mm  this approach is not effective.

As has already been mentioned above, the seeming viscosity and density of the distribution of erythrocytes along radius of a cylindrical tube play a very important role for the definition of the properties of a blood flow. In [10], the flow in narrow vessels is modeled under the assumption that the flow consists of two layers – the core rich in erythrocytes with hypothetic viscosity and the plasma layer that surrounds the core and is free of erythrocytes. Besides an additional rough surface is also introduced to simulate layers with a rarefied content of erythrocytes.

In paper [11], which is most closely related to the present study and is, in our opinion, the best model  among those known to us, an attempt is made on the basis of experimental data (in vitro) and simplified theoretical approach to define   the medium viscosity  in a narrow blood vessel of circular cross-section as a function of the radial coordinate  (naturally, assuming that the flow is axially symmetric), i.e. to define  using a prescribed velocity profile. However, the mathematical definition of the viscosity function does not look convincing in [11] since, according to this work, viscosity appears to be either constant or infinite on the flow axis.

Taken the above into account, we believe that our blood flow model based on a multilayer flow can provide a most exact and simplest representation of blood motion in vessels with lumen diameters from 15 mm to 80 mm. It should be noted that some researchers represent blood flows as three-layer or four-layer liquid flows.

Hence, unlike other authors, we assume that the rectilinear flow in narrow cylindrical vessels of elliptic or circular section is multilayer, where each layer has its own viscosity. The multilayer character, i.e. different viscosity value m for different layers is determined by the fact that densities of erythrocyte layers are different along the radius.

As for vessel cross-section geometry, in [12] preference is given to the elliptic cross-section, which is verified in [3] and [13], which indicate that under certain conditions the circular contour may be broken. Although in the forthcoming we deal with axially symmetrical flows in circular tubes, the obtained results can be extended to multilayer flows in elliptic tubes. This is important since it is much more natural to represent blood vessel cross-section as being elliptical.

Hence using the results obtained in this paper one can define the function  in a more exact and simple way (in particular,  can be represented as a step-function), if we assume, similar to [11], that the so-called velocity profile is defined experimentally.

The above-said indicates that it is advisable to use a multilayer flow in tubes of different cross- sections.

2. Fluid Flow Equations Attributed to Generalized Cylindrical Orthogonal Curvilinear Coordinates

Consider the stationary flow of a viscous incompressible fluid [14] in generalized cylindrical systems of coordinates  [2] with Lame’s coefficients  It is assumed that the displacement velocity vector , where u,v,w are the projections of the vector  on the normals to the coordinate surfaces  contains only the projection , i.e.

                    (1)

In this case, since equalities (1) are valid, the incompressibility condition is fulfilled, and the Navier-Stokes equation (where mass forces are absent) implies [14]

   (2)

Here, where P is hydrostatic pressure,  are normal stresses,  are tangential stresses,

   (3)

 is the fluid viscosity constant coefficient.

From formulas (2) and (3) it follows that

        (4)

Here p and b are constants.

Let us assume that an n-layer fluid flows along the z-coordinate in a four-faced prismatic tube with section

               (5)

(it is understood that the tube faces are not planes); the section of the first layer of the combined domain (5) is

 that of the second layer is  and that of the  n-th layer is  are constants where .

We denote the functions  the hydrostatic pressure  the constants p and b and the viscosity m in the k-th layer by ,  and , where

Let us now formulate the boundary-contact problem for a flow of an n-layer fluid in a prismatic tube. For the first layer

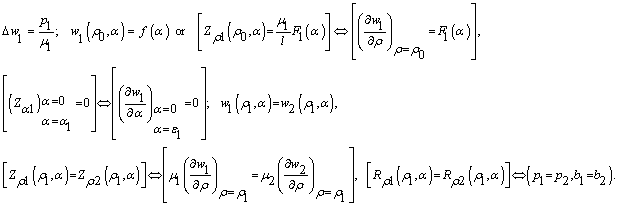        (6)

For the k-th layer when

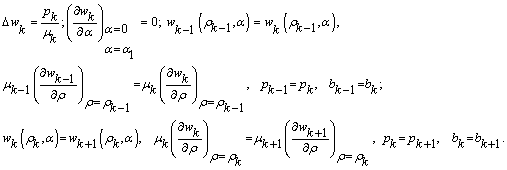                  (7)

For the n-th layer

                (8)

In formulas (6)-(8),  are the given functions. For   the condition    idealizes the tube face , assuming its internal surface is not resisting the fluid flow; in other words, it is assumed that there is no friction between the flowing fluid and the internal side of the tube face.

Note that the conditions

imply the conditions

where  are constants.

The function w is defined in the following manner:

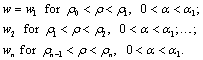            (9)

The functions  are defined analogously through the functions .

3. Solution of Boundary Value-Contact Problems in Various Generalized Cylindrical Coordinates

Cartesian coordinates  In this case, the coordinates  are replaced by the coordinates    .

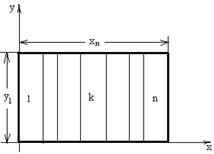
Fig. 1. The section of a rectangular linear tube with a multilayer fluid flowing in it.

Assuming that the functions  and  can be represented by Fourier trigonometric series in cosines, the solution of the boundary-contact problem (6)-(9) takes in the domain  the following form:

     (10)

whereThe constants  are defined from an infinite system of linear algebraic equations, which is obtained when the boundary and contact conditions are satisfied. The matrix of this infinite system of equations is block-diagonal, each block being a non-degenerate matrix.

If the functions  are equal to zero, then  and

,

the constants  being defined from the compatible system of 2n linear algebraic equations with 2n unknowns. It should be mentioned that the authors have never come across any publications dealing with multilayer flows in rectangular tubes.

We must also indicate that when we speak about the solution of this or that problem only analytical solutions are implied. Here and everywhere in the forthcoming what we have in mind are analytical solutions, which in some cases become exact.

Fig. 2. The section of a triangular rectilinear tube  with a multilayer fluid flowing in it.

Circular cylindrical coordinates  In this case, the coordinate r is replaced by the coordinate r, and the operation  is replaced by the operation  l=r,   Assuming the flow to be symmetrical with respect to the vertical plane passing across the coordinate z, we write

By virtue of the arguments used in the paragraph containing formula (10) the solution of the boundary-contact problem (6)-(9) in the circular cylindrical coordinate system takes in the domain  the following form:

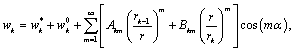   (11)

where  .

If  then the boundary condition  is replaced by the condition  while in formula (11) we should assume

If the functions   are equal to zero, then  and

                                      (12)

Furthermore, if in addition to this,, then

                                    (13)

For  where j=1,n, as has already been said, , and the constants  in formula (12) are defined from the compatible system of  2n (or 2n-1, in the case , in which formula (13) is used) of linear algebraic equations with 2n or (2n-1) unknowns (recall that the system of equations is obtained when the boundary and contact conditions are satisfied).

It should be noted that if the liquid flow is assumed to be homogeneous, we arrive at a well-known Poiseuille flow, though the problem of multilayer flows in circular tubes seems to have been stated and solved for the first time.

System of elliptic cylindrical coordinates  In this coordinate system  where c – is the scale multiplier,     like in the case of circular cylindrical coordinates we assume that

Fig. 3. The section of a semi-elliptic rectilinear tube ( or) with a multilayer fluid flowing in it.

By virtue of the arguments used for formula (10) the solution of the boundary-contact problem (6)-(9) in the elliptic cylindrical coordinate system takes the following form in the domain :

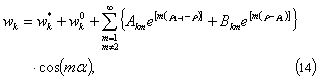
where

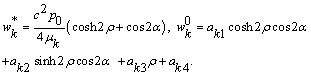
If  then the boundary condition  is replaced by the condition  and in formula (14) it should be assumed that

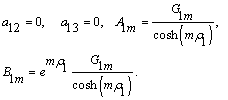
In the case where the functions  and  are equal to zero, we have  and

                           (15)

and if, in addition to this,  then

         (16)

For  where j=1,n, as has already been said, , and the constants  in formula (15) are defined from the compatible system of 4n (or of 4n-2 in the case  when formula (16) is used) of linear algebraic equations with 4n or (4n-2) unknowns.

If the flow is observed in an elliptic tube, then the problem is well-known from scientific publications. As for the liquid flow in confocal elliptic ring tubes, the solution of this kind of problem, as well as that of multilayer liquid flows in elliptic tubes, has been given for the first time.

System of parabolic cylindrical coordinates. In this coordinate system     it is assumed that 

Fig. 4. The section of a parabolic rectilinear tube with a multilayer fluid flowing in it.

In the considered coordinate system

While in formulas (6)-(9) the coordinates  exchange their places. By virtue of this fact and also the arguments used for formula (10), the solution of the boundary-contact problem (6)-(9) in the parabolic cylindrical coordinate system is sought in the domain  in the following form:

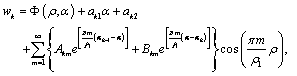  (17)

where We introduce here the notation

and represent the functions  as Fourier series in cosines

     (18)

where  is the natural number which guarantees the prescribed exactness of representation of the function  by trigonometric series in cosines. Note here that integral (18b) can be easily taken in explicit form.

The boundary-contact problem (6)-(9) is solved, i.e. the constants   are defined as a result of the substitution of formula (18a) into (17) and comparison of the respective series.

If  then the boundary condition  is replaced by the condition  and in formula  (17)  it should be assumed that

For  where  the constants  are defined from the compatible system  (or  in the case ) of linear algebraic equations with  or   unknowns.

We should indicate that the problem of stationary flows of homogeneous and multilayer liquids, which is discussed in this section, has been studied for the first time.

System of bipolar cylindrical coordinates r, a, z. In this coordinate system      it is assumed that When considering an n–layer flow in the bipolar cylindrical coordinate system,

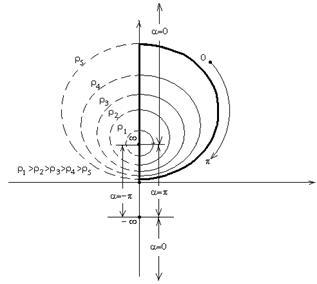
Fig. 5. The section of a semi-circular rectilinear tube with a multilayer fluid flowing in it eccentrically.

Before passing over to the construction of the solution of the boundary-contact problem (6)-(9), we will find a particular solution of equation (4b).

Using the expansion

we obtain

(19)

The latter formula leads to the equation

(20)

where  is the natural number which, according to formula (19), guarantees the prescribed exactness of the representation of the function  by a series.

By a straightaway verification we can make sure that a particular solution  of equation (20) can be represented as

         (21)

Taking into account the arguments used for formula (10), the solution of the boundary-contact problem (6)-(9) about an eccentric flow of a multi-layer fluid in a circular tube in the bipolar cylindrical coordinate system takes, in the domain , the following form

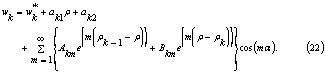
If  then the boundary condition  is replaced by the condition  and in formula (22) it should be assumed that

For the constants    are defined from the compatible system of  (or of  in the case) of linear algebraic equations with  or    unknowns.

Flows of homogeneous and multilayer liquids along tubes of eccentric circular ring cross-sections have been considered for the first time. Naturally, as it has been mentioned above, only analytical solutions are implied.

4. Circular Flows of Multilayer Fluids in Tubes of Rectangular Cross-Sections

In the circular cylindrical system of coordinates r, a, z consider a circular flow (along the coordinate a) of an n-layer fluid in the rectangular tube  ,  It is evident that the tube is bounded by cylindrical surfaces  and  and planes  and

In this case is assumed that

                   (23)

Then  the non-compressibility condition

implies

Besides, taking (23) into account and applying Newton’s law we have

then Navier-Stokes equations take the following form

               (24)

It is well-known that circular motion of a viscous incompressible liquid is plane-parallel ( is only a function of the radial coordinate r) and the general solution of (24) has the form [14]

where  are arbitrary constants.

The tangential stress  can be represented by the formula

Equality conditions of normal stresses on the contour  The following boundary conditions are satisfied

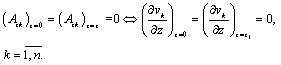
Besides on the boundary , on contact intervals   and on the boundary   the following boundary and contact conditions

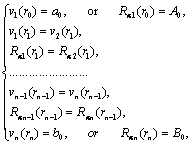          (25)

are imposed  where

  (26)

 (27)

Bearing (27) in mind, by virtue of contact conditions   we have

                        (28)

Hence formulas (26) and (27) take the following form

Substituting (28) in conditions (25) for the case when velocity values are defined on the boundaries  and  we obtain the following linear algebraic system of   equations with respect to coefficients

(29)

It can be easily shown that the determinant of system (29) is non-zero. Thus the stated problem has been solved.

Now consider the case when  Let

In this case

Since  by formula (28) we have

For the given case system of equations (29) takes the following form

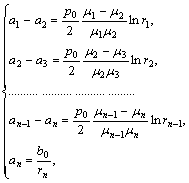
from which coefficients  can be easily obtained. For the velocity and pressure in the k-th layer we have the following formulas

The stress  is constant throughout the multilayer domain   and equals

Homogeneous liquid flows in circular tubes of rectangular cross-sections have been studied by a number of authors [14], while corresponding multilayer flows, like in the above-mentioned cases, have been considered for the first time.

5. Particular Application Example of Multilayer Axially Symmetric Flow

In this section we illustrate effective application of the above-stated and solved problems for the construction of a mathematical model of blood flow in narrow vessels with lumen (diameter) of 15-80 mm.

Let us have a closer look at axially symmetric flows of multilayer liquids in circular tubes, so that we could apply these results to the determination of radial changes of viscosity in circular blood vessels. The radial change of viscosity will be obtained as a piecewise constant function, or, in other words, in the form of a step function. Although it will be a step function, we hope it will provide a better approximation of actual viscosity distribution than a the continuous function in paper [11].

In connection with the above-stated let us consider the following problem: in a circular cylindrical tube based on a defined velocity profile choose a distribution of layers of constant thickness and different viscosity which will provide the closest approximation of the defined velocity profile to the theoretical profile obtained by us.

It should be particularly noted that the involved example does not describe some actual blood flows in blood vessels but rather illustrates the effectiveness and advantages of the proposed mathematical blood flow model.

The radius of the tube for an -layer flow is denoted by . Then from (11) we obtain for each -th layer

or assuming that ,     and mm  is the viscosity of the  -th layer

where

Let the thickness of each layer be The layers of different viscosity are arranged over the section as shown in Fig. 3. For clearness, let us consider the case

Fig. 6. The layers distribution scheme.

From the contact condition on the surface:   we obtain  (this equality follows from the expression    is the tangential stress, where  is a derivative with respect to .

From the condition  we have  and so on. Therefore all

Thus for any layer we have

This formula indicates that of two contact conditions one is the condition of the equality of velocities on the contact surfaces and the other is the condition of the equality of the velocity to zero on the vessel wall.

For each layer of the boundary-contact condition we write

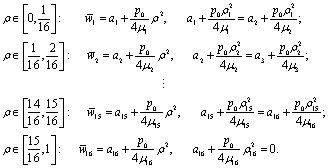
The above system makes it easy to define the coefficients

Using the method of mathematical induction and substituting the found values of   for each -th layer of the -layer fluid we obtain

where and  is a relative viscosity, where  is the viscosity of the -th layer and  is the viscosity of the layer free from plasma particles.

In the proposed model of a viscous fluid flow, the relative viscosities differ from each other because they have a different packing of erythrocytes in a cylindrical ring 1 mm. thick (see [1]).

In Fig.6 the viscosity of the layers   is equal to 10, while that of the layers   to 1.

In Fig.7 the dotted line denotes the given distribution of velocities along the radius and the broken line corresponds to the distribution of velocities along the same radius, we obtained by approximation.

The good coincidence of the continuous and the broken line in Fig. 7 guarantees the definition of the viscosity distribution with sufficiently high precision. This gives us the right to state that the proposed model works well.

 

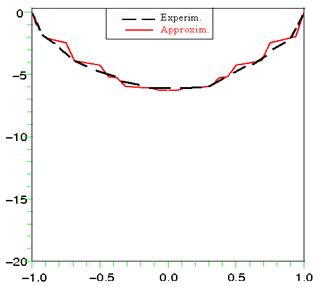
Fig. 7. The experimental and the approximate distribution of velocities with respect to the thickness.

6. Conclusion

In addition to well-known problems  a number of new boundary value problems (that are prevailing here) on stationary multilayer flows of viscous incompressible liquids have been stated and solved for the first time in the given work.  The multilayer flow (each fluid has its own viscosity) is considered in rectilinear tubes bounded by the coordinate surfaces of generalized cylindrical coordinates. The tube section contour, which is perpendicular to the tube generating, may be rectangular, circular, elliptic, parabolic and so on. Besides, the multilayer flow is considered in circular tubes of rectangular section (in the circular cylindrical coordinates) when the tube faces are planes and cylindrical surfaces.

At the end of the paper an example of axially symmetric flows of multilayer liquids is considered in detail, which illustrates the applicability of the proposed approach to blood flow studies in blood vessels of 15-80 mm lumen (diameter). It should be also noted that instead of multilayer axially symmetric flows in circular tubes, one could easily investigate multilayer flows in elliptical tubes, which would be even closer to the actual blood flow in blood vessels.

We mention that the presented model will provide an opportunity to determine such important parameters (values) in micro vessels, as liquid viscosity (more exactly, apparent viscosity), dynamical hematocrit and resistance force, caused by friction. All this are very important for the studies of blood microcirculation. And this, as specialists in biomedicine believe, is a prerequisite for medical clinical investigations.

To conclude the paper, we would like to indicate that the solutions of some of the problems considered by us are given in [17], while the fluid motion in a toroidal tube is considered in [18].

References

1. Happel J., Brenner G.: Hydrodynamics for small Reynolds numbers. Mir, Moscow (in Russian) (1976)
2. Bermant A.F.: Mapping Linear Coordinates. Transformation. Green's Formulas. Fizmatgiz, Moscow (in Russian) (1958)
3. Aleksander S. Popel and Paul C. Johnson: Microcirculation and Hemorheology. Ann..Rev. Fluid  Mech. 37: 43-69 (2005)
4. Mchedlishvili G.: Dynamic Structure of Blood in Microvessels. Microcirculation Endothelium and Lymphatic, vol. 7, Butterworth-Heinemann, 3-49 (1991)
5. Robert M. Berne, Matthew N. Levy.: Cardiovascular Physiology. The C.V. Mosby Company. Saint Louis (1972)
6. Caro C.C., Pedley T.J., Schoter R.C., Seed W.A.: The Mechanics of the Circulation. Oxford University Press. Oxford-New York- Toronto (1978)
7. Mchedlishvili G.  and Nobuji Maeda: Blood Flow Structure Related to Red Cell Flow. A Determinant of Blood Fluidity in Narrow Microvessels. Japanese Journal of Physiology 51: 19-30 (2001)
8. Skalak R.,  Chen P.H. and Chien S.: Effect of Hematocrit and Rouleaux on Apparent Viscosity in Capillaries. Biorheology 9: 67-82 (1972)
9. Masako Sugihara-Seki and Richard Skalak: Numerical Study of Asymmetric Flows of Red Calls in Capillaries. Microvascular Research 36: 64-74 (1988)
10. Sharan M. and Popel A.S.: A two phase model for flow of blood in narrow tubes with increased effective viscosity near the wall. Biorheology 38: 415-428 (2001)
11. David S. Long, Michael L. Smith, Axel R. Pries, Klaus Ley and Edward R. Damiano: Microviscometry reveals reduced blood viscosity and altered shear rate and shear stress profiles in microvessels after hemodilution, PNAS, July 6, vol. 101, no. 27, 10060-10065 (2004)
12. Krasnoperov K.A., Stoyan D.: Second-order stereology of spatial fibre systems. Journal of Microscopy 216(2): 156-164 (2004)
13. El-Kareh A.W., Secomb T.W.: A Model for red blood cell motion in bifurcating microvessels. International Journal of Mult. Phase Flow 26: 1545-1564 (2000)
14. Slezkin N.A.: Dynamics of a viscous incompressible fluid.  Gos. Izdat. Tekh. Teor. Literaturi, Moscow (in Russian) (1955)
15. Brown, J. W. and Churchill, R. V.: Fourier Series and Boundary value problems, 5^th ed. New York: McGraw-Hill (1993)
16. Bitsadze A.V. :Equations of mathematical physics, Mir Publishers  (Translated from Ruusian) (1980)
17. Khomasuridze N.G.: On some stationary multi-layer flows of viscous incompressible liquids. Proceedings of the International Scientific and Technical Conference "Architecture and Construction – Contemporary Problems", 15-18 October, Yerevan-Jermuk, 285-290 (in Russian) (2008)
18. Khomasuridze N., Ninidze K. and Siradze Z.: A steady flow of a viscous multi-layer fluid in a toroidal tube with small radius. Mem. Differential Equations. Math. Phys. 44: 151-154 (2008).