Fuzzy Logic as a Tool for Assessing Human Skills
Michael Gr. Voskoglou*
Department of Applied Mathematics, Faculty of Technological Applications, Graduate Technological Educational Institute of Western Greece, Patras, Greece
Abstract
In this paper we develop a method for assessing the overall performance of groups of individuals participating in any kind of human activities. For this, we represent each of the groups under assessment as a fuzzy subset of a set U of linguistic labels characterizing its members’ performance and we use the centre of gravity defuzzification technique in converting the fuzzy data collected from the corresponding activity to a crisp number. According to the above method the higher is an individual’s performance the more its "contribution" to the corresponding group’s overall performance (weighted performance). Two real life applications are also presented, related to the bridge players’ performance and the students’ assessment respectively, illustrating our assessment method in practice.
Keywords
Fuzzy Sets, Centre of Gravity (COG) Defuzzification Technique, Contract Bridge
Received: February 11, 2015
Accepted: March 7, 2015
Published online: March 12, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
There used to be a tradition in science and engineering of turning to probability theory when one is faced with a problem in which uncertainty plays a significant role. This tradition was justified when there were no alternative tools for dealing with the uncertainty. Today this is no longer the case. Fuzzy logic, which is based on fuzzy sets theory introduced by Zadeh [17] in 1965, provides a rich and meaningful addition to standard logic.
A real test of the effectiveness of an approach to uncertainty is its capability to solve problems which involve different facets of uncertainty. Fuzzy logic has a much higher problem solving capability than standard probability theory. Most importantly, it opens the door to construction of mathematical solutions of computational problems which are stated in a natural language. The applications which may be generated from or adapted to fuzzy logic are wide-ranging and provide the opportunity for modelling under conditions which are inherently imprecisely defined, despite the concerns of classical logicians (e.g. see Chapter 6 of [7], [10], [11] and its relevant references, [12-14], etc).
The methods of assessing the individuals’ performance usually applied in practice are based on principles of the bivalent logic (yes-no). However these methods are not the most suitable ones when dealing with ambiguous cases. In Education, for example, the teacher is frequently not absolutely sure about a particular numerical grade characterizing a student’s performance. Fuzzy logic, due to its nature of characterizing such ambiguous cases with multiple values, offers a wider and richer field of resources for this purpose.
In this paper we shall use principles of fuzzy logic for developing a general method for assessing the skills of groups of individuals participating in any human activity. The rest of the paper is organized as follows: In the next section we develop our fuzzy assessment method. In section three we present two real life applications illustrating our method in practice. Finally the last section is devoted to conclusions and discussion on the future perspectives of research in this area.
For general facts on fuzzy sets we refer to the book [9]
2. The Fuzzy Assessment Method
Let us consider a group, say H, of n individuals, where n is a positive integer, participating in a human activity (e.g. problem-solving, decision making, football match, a chess tournament, etc). Further, let U = {A, B, C, D, F} be a set of linguistic labels characterizing the individuals’ performance with respect to the above activity, where A characterizes an excellent performance, B a very good, C a good, D a fair and F an unsatisfactory performance respectively. Obviously, the above characterizations are fuzzy depending on the user’s personal criteria, which however must be compatible to the common logic, in order to be able to model the real situation in a worthy of credit way.
A classical way for assessing the overall group’s performance with respect to the corresponding activity is to express the levels of the individuals performance in numerical values and then to calculate the mean of their performance in terms of these values (mean group’s performance).
Here, we shall use principles of fuzzy logic for developing an alternative method of assessment, according to which the higher is an individual’s performance, the more its "contribution" to the group’s total performance (weighted group’s performance). For this, we are going to represent H as a fuzzy subset of U. In fact, if nA, nB. nC, nD and nF denote the number of the individuals of H that had demonstrated an excellent, very good, good, mediocre and unsatisfactory performance respectively, we define the membership function m : U ![]() [0,1] as follows:
[0,1] as follows:
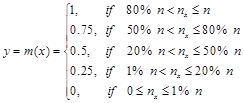 (1)
(1)
for each x in U.
Then H can be written as a fuzzy subset of U in the form: H = {(x, m(x)): x![]() U}.
U}.
In converting the fuzzy data collected from the corresponding activity to a crisp number we shall make use of a very popular in fuzzy logic defuzzification method known as the centre of gravity (COG) technique ([9], etc). For this, we correspond to each x of the universal set U an interval of values from a prefixed numerical distribution, which actually means that we replace U with a set of real intervals. Then, we construct the graph of the corresponding membership function y=m(x). There is a commonly used in fuzzy logic approach to represent the fuzzy data with the pair of numbers (xc, yc) as the coordinates of the COG, say Fc, of the level’s section F contained between the above graph and the OX axis, which we can calculate using the following well-known (e.g. see [15]) formulas:
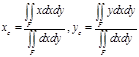 (2)
(2)
Here we shall adapt the COG technique to be used as an assessment method [8,13,14]. For this, we characterize an individual’s performance as unsatisfactory (F), if x ![]() [0, 1), as fair (D), if x
[0, 1), as fair (D), if x ![]() [1, 2), as good (C), if x
[1, 2), as good (C), if x![]() [2, 3), as very good (B), if x
[2, 3), as very good (B), if x ![]() [3, 4) and as excellent (A), if x
[3, 4) and as excellent (A), if x ![]() [4,5] respectively. In other words, if x
[4,5] respectively. In other words, if x ![]() [0, 1), then y1=m(x) = m(F), if x
[0, 1), then y1=m(x) = m(F), if x ![]() [1, 2), then y2=m(x)= m(D), etc.
[1, 2), then y2=m(x)= m(D), etc.
Therefore in our case the graph of the membership function attached to H is the bar graph of Figure 1 consisting of five rectangles, say Si, i=1,2,3, 4, 5, whose sides lying on the X axis have length 1. In this case ![]() is the area of F which is equal to
is the area of F which is equal to![]()
Also
![]()
![]()
![]()
![]() ,
,
and
![]() =
=![]() =
=![]() .
.
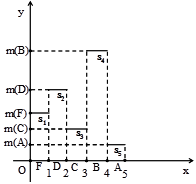
Figure 1. Bar graphical data representation
Therefore formulas (2) are transformed into the following form:
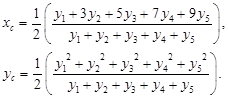
Normalizing our fuzzy data by dividing each m(x), x![]() U, with the sum of all membership degrees we can assume without loss of generality that y1+y2+y3+y4+y5 = 1. Therefore we can write:
U, with the sum of all membership degrees we can assume without loss of generality that y1+y2+y3+y4+y5 = 1. Therefore we can write:
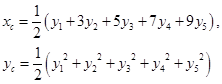 (3)
(3)
with yi = 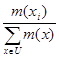 .
.
But, 0![]() (y1-y2)2=y12+y22-2y1y2, therefore y12+y22
(y1-y2)2=y12+y22-2y1y2, therefore y12+y22 ![]() 2y1y2, with the equality holding if, and only if, y1=y2. In the same way one finds that y12+y32
2y1y2, with the equality holding if, and only if, y1=y2. In the same way one finds that y12+y32 ![]() 2y1y3, with the equality holding if, and only if, y1=y3 and so on. Hence it is easy to check that (y1+y2+y3+y4+y5)2
2y1y3, with the equality holding if, and only if, y1=y3 and so on. Hence it is easy to check that (y1+y2+y3+y4+y5)2![]() 5(y12+y22+y32+y42+y52), with the equality holding if, and only if, y1=y2=y3=y4=y5. But y1+y2+y3+y4+y5 =1, therefore 1
5(y12+y22+y32+y42+y52), with the equality holding if, and only if, y1=y2=y3=y4=y5. But y1+y2+y3+y4+y5 =1, therefore 1 ![]() 5(y12+y22+y32+y42+y52) (4), with the equality holding if, and only if, y1=y2=y3=y4=y5=
5(y12+y22+y32+y42+y52) (4), with the equality holding if, and only if, y1=y2=y3=y4=y5=![]() .
.
Then the first of formulas (3) gives that xc = ![]() . Further, combining the inequality (4) with the second of formulas (3), one finds that 1
. Further, combining the inequality (4) with the second of formulas (3), one finds that 1![]() 10yc, or yc
10yc, or yc ![]()
![]() . Therefore the unique minimum for yc corresponds to the centre of gravity Fm (
. Therefore the unique minimum for yc corresponds to the centre of gravity Fm (![]() ,
,![]() ).
).
The ideal case is when y1=y2=y3=y4=0 and y5=1. Then from formulas (3) we get that xc = ![]() and yc =
and yc = ![]() .Therefore the centre of gravity in this case is the point Fi (
.Therefore the centre of gravity in this case is the point Fi (![]() ,
, ![]() ).
).
On the other hand, in the worst case y1=1 and y2=y3=y4= y5=0. Then by formulas (3), we find that the centre of gravity is the point Fw (![]() ,
, ![]() ).
).
Therefore the "area" where the centre of gravity Fc lies is represented by the triangle Fw Fm Fi of Figure 2. Then from elementary geometric considerations it follows that the greater is the value of xc the better is the corresponding group’s performance. Also, for two groups with the same xc ![]() 2,5, the group having the centre of gravity which is situated closer to Fi is the group with the higher yc; and for two groups with the same xc <2.5 the group having the centre of gravity which is situated farther to Fw is the group with the lower yc. Based on the above considerations it is logical to formulate our criterion for comparing the groups’ performances in the following form:
2,5, the group having the centre of gravity which is situated closer to Fi is the group with the higher yc; and for two groups with the same xc <2.5 the group having the centre of gravity which is situated farther to Fw is the group with the lower yc. Based on the above considerations it is logical to formulate our criterion for comparing the groups’ performances in the following form:
• Among two or more groups the group with the higher xc performs better.
• If two or more groups have the same xc ³ 2.5, then the group with the higher yc performs better.
• If two or more groups have the same xc < 2.5, then the group with the lower yc performs better.
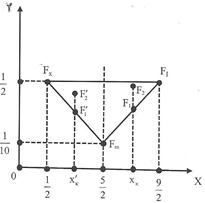
Figure 2. Graphical representation of the "area" of the centre of gravity
3. Applications
In this section we shall present two real life applications illustrating in practice the importance of our results obtained in the previous section. The first of these applications concerns a new assessment method of the bridge players’ performance, while the second one is related to the assessment of students’ performance.
3.1. Anew Assessment Method of the Bridge Players’ Performance
Contract bridge is a card game belonging to the family of trick-taking games. It occupies nowadays a position of great prestige being, together with chess, the only mind sports (i.e. games or skills where the mental component is more significant than the physical one) officially recognized by the International Olympic Committee. Millions of people play bridge worldwide in clubs, tournaments and championships, but also on line (e.g. [1]) and with friends at home, making it one of the world’s most popular card games.
A match of bridge can be played either among teams (two or more) of four players (two partnerships), or among pairs. For a pairs event a minimum of three tables (6 pairs, 12 players) is needed, but it works better with more players. At the end of the match in the former case the result is the difference in International Match Points (IMPs) between the competing teams and then there is a further conversion, in which some fixed number of Victory Points (VPs) is appointed between the teams. It is worthy to notice that the table converting IMPs to VPs has been obtained through a rigorous mathematical manipulation [4].
On the contrary, the usual method of scoring in a pairs’ competition is in match points. Each pair is awarded two match points for each pair who scored worse than it on each game’s session (hand), and one match point for each pair who scored equally. The total number of match points scored by each pair over all the hands played is calculated and it is converted to a percentage. However, IMPs can also used as a method of scoring in pair events. In this case the difference of each pair’s IMPs is usually calculated with respect to the mean number of IMPs of all pairs.
For the fundamentals and the rules of bridge, as well as for the conventions usually played between the partners we refer to the famous book [6] of Edgar Kaplan (1925-1997), who was an American bridge player and one of the principal contributors to the game. Kaplan’s book was translated in many languages and was reprinted many times since its first edition in 1964. There is also a fair amount of bridge-related information on the Internet, e.g. see web sites [2,3], etc.
The Hellenic Bridge Federation (HBF) organizes, on a regular basis, simultaneous bridge tournaments (pair events) with pre-dealt boards, played by the local clubs in several cities of Greece. Each of these tournaments consists of six in total events, played in a particular day of the week (e.g. Wednesday), for six successive weeks. In each of these events there is a local scoring table (match points) for each participating club, as well as a central scoring table, based on the local results of all participating clubs, which are compared to each other. At the end of the tournament it is also formed a total scoring table in each club, for each player individually. In this table each player’s score equals to the mean of the scores obtained by him/her in the five of the six in total events of the tournament. If a player has participated in all the events, then his/her worst score is dropped out. On the contrary, if he/she has participated in less than five events, his/her name is not included in this table and no possible extra bonuses are awarded to him/her.
In case of a pairs’ competition with match points as the scoring method and according to the usual standards of contract bridge, one can characterize the players’ performance, according to the percentage of success, say p, achieved by them, as follows:
• Excellent (A), if p > 65%.
• Very good (B), if 55% < p![]() 65%.
65%.
• Good (C), if 48% < p![]() 55%.
55%.
• Mediocre (D), if 40% ![]() p
p![]() 48%.
48%.
• Unsatisfactory (F), if p < 40 %. 1
Our application presented here is related to the total scoring table of the players of a bridge club of the city of Patras, who participated in at least five of the six in total events of a simultaneous tournament organized by the HBF, which ended on February 19, 2014 (see results in [5]). Nine men and five women players are included in this table, who obtained the following scores. Men: 57.22%, 54.77%, 54.77%, 54.35%, 54.08%, 50.82 %, 50.82%, 49.61%, 47.82%. Women: 59.48%, 54.08%, 53.45%, 53.45%, 47.39%. The above results give a mean percentage of approximately 52.696% for the men and 53.57% for the women players. Therefore the women demonstrated a slightly better mean performance than the men players, their difference being only 0.874%.
The above results are summarized in Table 1, the last column of which contains the corresponding membership degrees calculated with respect to the membership function defined by the formula (1) of the previous section. For example, in the case of men players we have n = 9, 1% n = 0.09, 20% n = 1.8, 50% n = 4.5, 80% n =7.2, nA = nF = 0, nB = nD = 1, nC = 7, which give that m(A) = m(B) )= m(F) = 0, m(B) = m(D) = 0.25 and m(C)= 0.75
Table 1. Total scoring of the men and women players
Men
| % Scale | Performance | Number of players | m(x) |
| >65% | A | 0 | 0 |
| 55-65% | B | 1 | 0.25 |
| 48-55% | C | 7 | 0.75 |
| 40-48% | D | 1 | 0.25 |
| <40% | F | 0 | 0 |
| Total | 9 | 1.25 |
Women
| % Scale | Performance | Number of players | m(x) |
| >65% | A | 0 | 0 |
| 55-65% | B | 1 | 0.25 |
| 48-55% | C | 3 | 0.75 |
| 40-48% | D | 1 | 0.25 |
| <40% | F | 0 | 0 |
| Total | 5 | 1.25 |
Then, normalizing the membership degrees and applying formulas (3) of the previous section, we find that ![]() =2.5 and yc=
=2.5 and yc=![]() = 0.22 for both the men and women players.. Thus, according to our criterion (second case) stated in the previous section, and in contrast to their mean performance, the men demonstrated an identical weighted performance with the women players.
= 0.22 for both the men and women players.. Thus, according to our criterion (second case) stated in the previous section, and in contrast to their mean performance, the men demonstrated an identical weighted performance with the women players.
In concluding, our new assessment method of the bridge players’ performance can be used as a complement of the usual scoring methods of the game (match points or IMPs) in cases where one wants to compare (for statistical or other reasons) the overall performance of special groups of players (e.g. men and women, young and old players, players of two or more clubs participating in a big tournament, etc).
3.2. Students’ Assessment
The students of two different Departments of the School of Management and Economics of the Graduate Technological Educational Institute of Western Greece achieved the following scores (in a climax from 0 to 100) at their common progress exam in the course "Mathematics for Economists I":
Table 2. Students’ scores
Department 1
| % Scale | Grade | Number of Students | m(x) |
| 89-100 | A | 3 | 0.25 |
| 77-88 | B | 21 | 0.5 |
| 65-76 | C | 28 | 0.5 |
| 53-64 | D | 22 | 0.5 |
| Less than 53 | F | 16 | 0.25 |
| Total | 90 | 2 |
Department 2
| % Scale | Grade | Number of students | m(x) |
| 89-100 | A | 1 | 0 |
| 77-88 | B | 10 | 0.25 |
| 65-76 | C | 37 | 0.5 |
| 53-64 | D | 31 | 0.5 |
| Less than 53 | F | 21 | 0.5 |
| Total | 100 | 1.75 |
Normalizing the membership degrees and applying formulas (3), we find
![]()
for the first and
![]()
for the second Department, which means that the first Department demonstrated a better performance.
4. Conclusions and Discussion
In the present paper we developed a general fuzzy method for assessing the overall performance of groups of individuals participating in any kind of human activity. Our method is very simple to its application in practice needing no complicated calculations in its final step, as it happens with other assessment methods (e.g. measurement of the system’s uncertainty [11]). For developing this method we represented each of the groups under assessment as a fuzzy subset of a set U of linguistic labels characterizing their members’ performance and we used the COG defuzzification technique for converting the fuzzy data collected from the corresponding activity to a crisp number. According to the above assessment method the higher is an individual’s performance the more its "contribution" to the corresponding group’s total performance (weighted performance). Thus, in contrast to the mean of the scores of all the group’s members, which is connected to the mean group’s performance, our method is connected somehow to the group’s quality performance. Consequently, when the above two different assessment methods are used in comparing the performance of two or more groups of individuals, the results obtained may differ to each other (e.g. see our bridge application). Two applications were also presented, related to the bridge players’ performance and to the students’ assessment respectively, illustrating the importance of our assessment method in practice.
Our future plans for further research on the subject aim at applying our new assessment method in more bridge matches (including also games played with IMPs) and problem solving (not only mathematical) applications in order to get statistically safer and more solid conclusions about its applicability and usefulness. In a wider spectre, since our method is actually a general assessment method, it could be interesting to be applied in more sectors of the human activity, including other competitive games (e.g. other card games, chess, backgammon, etc), collective and individual sports, human cognition and learning, Artificial Intelligence, Biomedical Sciences, Management and Economics, etc.
References
- Bridge Base Online (BBO), www.bridgebase.com/index.php?d=y, accessed on March 29, 2014
- Bridge rules and variations, www.pagat.com/boston/bridge.html, accessed on March 29, 2014
- Contract bridge, http://en.wikipedia.org/wiki/contract_bridge, accessed on March 29, 2014
- D’Orsi, E. (chair) et al., The New WBF IMP to VP Scales, Technical Report of WBF Scoring,www.worldbridge.org/Data/Sites/1/media/documents/regulations/WBFAlgorithms.pdf, accessed on March 29, 2014
- Hellas Bridge Federation (in Greek), www.hellasbridge.org, accessed on March 31, 2014
- Kaplan, E. (2010), Winning Contract Bridge, Courier Dover Publications, N. Y.
- Klir, G. J. & Folger, T. A. (1988), Fuzzy Sets, Uncertainty and Information, Prentice-Hall, London.
- Subbotin, I. Ya., Badkoobehi, H. & Bilotckii, N. N. (2004), Application of fuzzy logic to learning assessment, Didactics of Mathematics: Problems and Investigations, 22: 38-41.
- van Broekhoven, E. & De Baets, B., Fast and accurate centre of gravity defuzzification of fuzzy system outputs defined on trapezoidal fuzzy partitions, Fuzzy Sets and Systems, 157(7), 904-918, 2006.
- Voskoglou, M. Gr., Fuzzy Sets in Case-Based Reasoning, Fuzzy Systems and Knowledge Discovery, IEEE Computer Society, Vol. 6, 52-256, 2009
- Voskoglou, M. Gr., Stochastic and fuzzy models in Mathematics Education, Artificial Intelligence and Management, Lambert Academic Publishing, Saarbrucken, Germany, 2011
- Voskoglou, M. Gr., Fuzzy Logic and Uncertainty in Mathematics Education, International Journal of Applications of Fuzzy Sets and Artificial Intelligence, 1,45-64, 2011
- Voskoglou, M. Gr., A Study on Fuzzy Systems, American Journal of Computational and Applied Mathematics, 2(5), 232-240, 2012
- Voskoglou, M. Gr. & Subbotin, I. Ya., Dealing with the Fuzziness of Human Reasoning, International Journal of Applications of Fuzzy Sets and Artificial Intelligence, 3, 91-106, 2013
- Wikipedia, Center of mass: Definition, available in the Web at: http://en.wikipedia.org/wiki/Center_of_mass#Definition, visited on October 10, 2014.
- Zadeh, L. A. (1965), Fuzzy Sets, Information and Control, 8: 338- 353.
Footnotes
[1] In an analogous way one could characterize the players’ performance in bridge games played with IMPs, with respect to the VPs gained.



