A Special Class of Tensor Product Surfaces with Harmonic Gauss Map

Azam Etemad Dehkordy^*

Department of Mathematical sciences, Isfahan University of Technology, Isfahan, Iran

Abstract

In this paper, we stat a necessary and sufficient condition for Gauss map of the tensor product of planar unite circle and a special smooth curve in En to be harmonic. In this way, we construct two orthonormal basis for the tangent space and the normal space of the resulting tensor product surface. As a direct consequence of these basis, we also get a result about shape operators of this surface.

Keywords

Tensor Product, Gauss Map, Harmonic Map

Received: February 3, 2015
Accepted: April 9, 2015
Published online: April 17, 2015

@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/

1. Introduction

The tensor product of two immersions of a given Riemannian manifold was introduced by Chen in the late 1970,s ([3]). This notion is a generalization of the quadratic representation of a submanifold.

In a special case, a tensor product surface is obtained by taking the tensor product of two curves. A number of properties such as minimality and totally reality are studied about tensor product of two planar curves ([7]). Moreover, minimal and pseudo- minimal tensor product of Lorentzian planar curve and an Euclidean planar curve is considered by Mihai ([8]).

Gauss map is one of the topics in differential geometry. On the other hand, harmonic functions have very useful properties in advanced mathematics.  So, we study the tensor product surfaces of two curves that have harmonic Gauss map.

2. Preliminaries

In this section, we recall some standard definitions and results from Riemannian geometry. Let M be an n-dimensional manifold, Em be an m-dimensional Euclidean space and  be an isometric immersion, as well as the Levi-Civita connection of  and  the induced connection on  from  We denote the second fundamental form of   in  by  normal connection in the normal bundle of  by  and the shape operator in the direction of normal vector field n by . It is well known that the two later notions are related to each other by

< II(X, Y ),n >=<,Y >                         (1)

where  and  are tangent vector fields to  For an n-dimensional submanifold  in  the mean curvature vector  is given by

If  then the submanifold is said to be minimal. A submanifold is called totally geodesic if  Furthermore, the Gaussian and Weingarten formula are given, respectively, by

                            (2)

                             (3)

Using above notations, we have the following Ricci equation,

1                        (4)

for tangent vector fields and normal vector fields   and

Let  be the Grassmannian consisting of all oriented n-planes through the origin of  For an isometric immersion  the Gauss map  of    is a smooth map which carries  into the oriented n-plane in , which obtained from the parallel  translation of  , the tangent space of   at  in . We known that    canonically imbedded in , the vector space obtained by the exterior product of  vectors in . We can assume  as Euclidean space  where , so the Gauss map at  can be written as  )(p), where  is an adapted local orthonormal frame field in  such that   are tangent to  and  are normal to If   be the set of real smooth functions on , then the Laplacian of  is defined by

                    (5)

Note that in this context, smooth can be replaced by

3. A Special Tensor Product Surface in

Let  be the unit planar circle centered at the origin with parameterization ) and be a unit speed smooth curve in  with parametrization  Here, we consider  for every (index 1 can be replaced by   The tensor product surface  of two curves  and  is given by,

Assume that  defines an isometric immersion of into   Let prime denote derivative with respect to It is easily seen that

and

form an orthonormal frame for tangent space of . Moreover, an orthonormal basis normal to  is given by

where

  and  .

If we use the following abbreviation,

and for

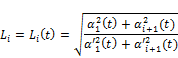
also for we us

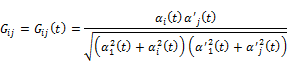
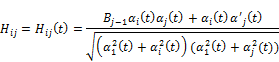
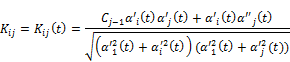
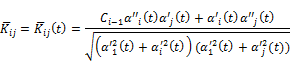
we get,

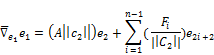
               (6)

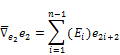
and for  we have,

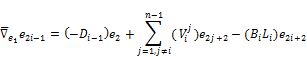
                                                            (7)

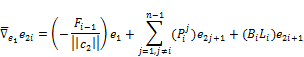
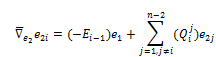
where   and ’s are in

 and

One immediate result that follows from (3) and (7) is following Corollary.

Corollary. Let be the tensor product surface of the circle ) and unit speed smooth curve ,  then for , , we have

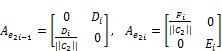              (8)

The following Theorem provides us a necessary and sufficient condition for our special tensor product surface to have harmonic Gauss map

Theorem. Let be a tensor product surface of the circle ) and unit speed smooth curve of plane.

Proof. If we use (5), (6) and (7), then a direct computation shows that the Laplacian of the Gauss map  is given by

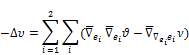
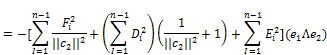
              (9)

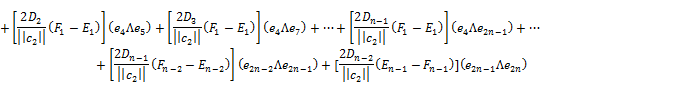
where for

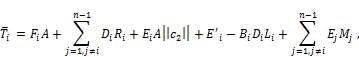
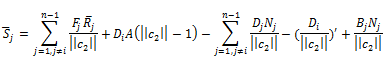
 and .

In definitions of  and , prime means the derivation respect to . If the Gauss map of   is harmonic, i.e. , then (9) implies that

                       (10)

 , ...,   ,

,  

Since all terms on the right-hand side of the first equation in (10) are nonnegative, hence we have

for This result and (8), show that  is a  totally geodesic surface in  and so  is a part of a plane. The converse is obvious.

4. Conclusion

The main conclusion of this paper is a planar surface in even dimensional Euclidean space can be obtained from tensor product of unit circle with a unit speed curve in an Euclidean surface of half dimension.

References

1. Yu. A. Aminov, The Geometry of Submanifolds, Gordon and Breach Science Publications, Amsterdam, 2001.
2. K. Arslan, B. Bulca, B. Kilic, Y. H. Kim, C. Murathan and G.Ozturk; Tensor Product Surfaces with Pointwise 1-type Gauss map, Bull. Korean Math. Soc. 48(2011), 601-607.
3. B. Y. Chen, Geometry of submanifolds, I: General Theory, Pure and Applied Mathematics, 22, Marcel Dekker, New York,1973.
4. B. Y. Chen, Differential Geometry of semiring of immersions, I: General Theory, Bull.Inst. Math. Acad. Sinica 21(1993), 1-34.
5. F. Decruyenaere, F. Dillen, I. Mihai and L. Verstraelen, Tensor products of spherical and equivariant immersions,, Bull. Belg. Math. Soc. Simon Stevin 1(1994), no.5, 643-648.
6. F. Decruyenaere, F. Dillen, L. Verstraelen and L. Vrancken, The semiring of immersions of manifolds, Beltrage zur Algebra und Geometrie, Contributions to Algebra and Geometry, Volume 34(1993), No.2, 209-215.
7. W. Goemans, I. v. deWoestyne, L. Vrancken, Minimal tensor product surfaces of two pseudo-Euclidean curves, Balkan Journal of Geometry and its Applications,Vol.16(2011), No.2, 62-69.
8. Y. H. Kim and D. W. Yoon, On the Gauss map of ruled surfaces in Minkowski spaces, Rocky Mountain J. math. 35(2005), No.5,1555-1581.
9. I. Mihai, R. Rosca, L. Vrstraelen and L. Vrancken, Tensor product Surfaces of Euclidean planar curves, Rendiconti del Seminrio Matematico di Messina, Serie II, 3,18(1994/1995),173-184.
10. I. Mihai, I. Van de Woestyne, L. Verstraelen and J. Walrave, Tensor product surfaces of a Lorentzian plane curve and a Euclidean plane curve, Rendiconti del Seminrio Matematico di Messina, Serie II, 3, 18(1994/1995), 147-158.
11. B. O’Neill, Semi-Riemannian Geometry and Applications to Relativity, Academic press New York,(1983).5.