Chemical Reaction and Soret Effects on Unsteady MHD Flow of a Viscoelastic Fluid Past an Impulsively Started Infinite Vertical Plate with Heat Source/Sink
S. Mohammed Ibrahim, K. Suneetha
Dept of Mathematics, Priyadarshini College of Engineering & Technology, Nellore, A. P, India
Abstract
An analytical solution of unsteady magnetohydrodynamic flow of visco-elastic fluid past an impulsively started infinite vertical plate in presence of chemical reaction, Soret and heat source/sink is studied. The governing equations are solved analytically using a regular perturbation technique. The expressions for velocity, temperature and concentration fields are obtained. With the aid of these, the expressions for the coefficient of skin friction, the rate of heat transfer in the form of Nusselt number and the rate of mass transfer in the form of Sherwood number are derived. Finally the effects of various physical parameters of the flow quantities are studied with the help of graphs and tables.
Keywords
MHD, Heat Source/Sink, Chemical Reaction, Soret Number, Visco-Elastic Fluid
Received: December 16, 2014
Accepted: December 31, 2014
Published online: January 23, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
Viscoelasticity is the property of materials that exhibit both viscous and elastic characteristics when undergoing deformation. Viscous materials, like honey, resist shear flow and strain linearly with time when a stress is applied. Elastic materials strain instantaneously when stretched and just as quickly return to their original state once the stress is removed. The understanding of viscoelastic fluid flow characteristics is of great interest for polymer and food processing industries. Unlike the Newtonian flow that is well understood, the flow of viscoelastic fluids is still a subject of great discussion. Most of the works on viscoelastic fluids found in literature treats internal flows using the geometry known as abrupt planar contraction. This is due mainly because this geometry was adopted as standard for viscoelastic fluids flow studies in 1987 during the fifth international workshop on numeric methods for non-Newtonians fluids (Hassager, [1]). On the other hand, simulations using free surface viscoelastic flow are receiving a special attention mainly in the last two decades (Tomé et al., [2]). Rajagopal et al. [3] examined for a special class of viscoelastic fluids known as second order fluids. Siddappa et al. [4] studied the flow of visoelastic fluids of the type Walter’s liquid B past a stretching sheet.
Many engineering problems are susceptible to MHD analysis .The study of MHD flow problems has achieved remarkable interest due to its application in MHD generators, MHD pumps and MHD flow meters etc. Cowling [5] and Crammer and Pai [6] have presented the importance of magnetohydrodynamic in their literature. Chang and Yen [7] discussed the magnetohydrodynamic flow through a channel under time dependent pressure gradient. MHD flow past an impulsively started infinite vertical plate with radiation was studied by Mazumdar and Deka [8]. Chowdhury and Islam [9] analyzed a two-dimensional unsteady MHD free convection flow of an incompressible, visco-elastic fluid past an infinite vertical porous plate.
The study of heat and mass transfer with chemical reaction is of great practical importance to engineers and scientists because of its almost universal occurrence in many branches of science and engineering. Possible applications of this type of flow can be found in many industries like power industry and chemical process industries. The importance of mass transfer with chemical reaction was explained by Astarita [10]. Apelblat [11] discussed the first order chemical reaction effect of axial diffusion with mass transfer. Saravana et al. [12] presented a finite difference method to the flow of visco-elastic second order Rivilin-Erickson fluid past an impulsively started infinite vertical plate in presence of a foreign mass and constant mass flux on taking into account of viscous dissipative heat at the plate heat and mass transfer under the influence of a uniform transverse magnetic field. The effects of mass transfer on flow past an impulsively started infinite vertical plate with constant heat flux and chemical reaction have been studied by Das et al. [13]. Heat and mass transfer effect on steady MHD viscoelastic fluid flow through a porous medium over a stretching surface in presence of chemical reaction has been studied Alharbi et al [14]. Sivaraj and Rushi Kumar [15] studied the chemical reaction effect on dusty viscoelastic fluid flow in an irregular channel in presence of convective boundary conditions. Unsteady free convective MHD flow of a visco-elastic fluid past an infinite vertical porous plate in rotating frame in presence of chemical reaction is investigated by Dash et al. [16].
The study of heat source/sink effects on heat transfer is very important because its effects are crucial in controlling the heat transfer and in cooling processes. Bodosa and Borkakati [17] have investigated MHD flow and heat transfer of Rivlin-Ericksen fluid through an inclined channel with heat source/sinks. Abo-Eladahab and El-Aziz [18] studied the effects of heat source/sink on MHD mixed convection flow from an inclined continuous stretching surface with blowing/suction. Bataller [19] proposed the heat source/sink and radiation effects on flow of a viscouselastic fluid over a stretching sheet. Abel and Nandeppanavar [20] investigated the heat transfer effect on steady MHD viscoelastic boundary layer flow over a stretching surface in presence of heat source/sink. Vajravelu and Hadyinicolaou [21] studied the convection heat transfer in an electrically conducting fluid near an isothermal stretching sheet with effect of heat source/sink. Umamaheswar et al. [22] considered an unsteady MHD viscoelastic, dissipative fluid flow embedded in a porous medium in presence of ohmic heating and heat source/sink. Kinyanjuli et al. [23] studied the effects of heat generating and radiation absorption on MHD free convection heat and mass transfer fluid past an impulsively started infinite vertical porous plate with hall current.
Fourier’s law, for instance, described the relation between energy flux and temperature gradient. In other format, Fick’s law was determined by the correlation of mass flux and concentration gradient. Moreover, it was noticed that energy flux can also be generated by composition gradients, pressure gradients, or body forces. The energy flux caused by a composition gradient was discovered in 1873 by Dufour and was correspondingly referred to the Dufour effect. It was also named as diffusion-thermo effect. On the other hand, mass flux can also be created by a temperature gradient, as was established by Soret. This is the thermal-diffusion effect. The thermal-diffusion effect has been utilized for isotope separation and in mixtures between gases with very light molecular weight (H2, He) and of medium molecular weight (N2, air). Olajuwon and Oahimire [24] examine the Soret and chemical reaction effects on MHD micropolar fluid with heat generation, heat and mass transfer. Bhavana et al. [25] analyzed the Soret effect on unsteady MHD flow past over a vertical plate in presence of heat source. Unsteady MHD free convection flow of an incompressible non-Newtonian viscoelastic fluid past an infinite vertical plate in presence of a heat source and soret effect was discussed by Choudhary and Sharma [26]. Ahmed [27] considered the effects of Soret and heat source on steady MHD flow in presence of heat and mass transfer. A Soret and radiation effect on MHD free convective flow from an impulsively started infinite vertical plate was studied by Ahmed [28]. Turkyilmazoglu and Pop [29] examined the effects of Soret and heat source on unsteady MHD free convection flow from an impulsively started infinite vertical plate in presence of thermal radiation.
The aim of the present paper was to study the effects of Soret and chemical reaction on unsteady MHD flow of a viscoelastic fluid past an impulsively started infinite vertical plate in presence of viscous dissipation and heat source/sink. The flow is governed by a couple non-linear systems of partial differential equations. These equations are solved by using perturbation technique. The effects of various governing parameters on the velocity, temperature, concentration, skin-friction coefficient, the Nusselt number, and Sherwood number are shown in the figures and tables and analyzed in detail.
2. Formulation of the Problem
Consider the flow of a viscous incompressible, visco-elastic second order Rivlin-Erickson fluid past an impulsively started infinite vertical plate with heat source in the presence of chemical reaction and Soret taking into an account. The ![]() -axis is taken along the plate in the vertically upward direction and the
-axis is taken along the plate in the vertically upward direction and the ![]() -axis is chosen normal to the plate. Initially the temperature of the fluid
-axis is chosen normal to the plate. Initially the temperature of the fluid ![]() , and the species concentration at the plate
, and the species concentration at the plate ![]() and in the fluid throughout
and in the fluid throughout ![]() are assumed to be the same. At time
are assumed to be the same. At time ![]() >0, the plate temperature is changed to
>0, the plate temperature is changed to ![]() causing convection currents to flow near the plate and mass is supplied at a constant rate to the plate and the plate starts moving upward due to impulsive motion, gaining a velocity of
causing convection currents to flow near the plate and mass is supplied at a constant rate to the plate and the plate starts moving upward due to impulsive motion, gaining a velocity of ![]() . A uniform magnetic field of intensity
. A uniform magnetic field of intensity ![]() is applied in the y-direction.
is applied in the y-direction.
Therefore the velocity and the magnetic field are given by ![]() q=(u,0,0) and B=(0,
q=(u,0,0) and B=(0,![]() ,0) the flow being slightly conducting the magnetic Reynolds number is much less then unity and hence the induced magnetic field can be neglected in comparison with the applied magnetic field in the absence of any input electric field ,the flow is governed by the following equations:
,0) the flow being slightly conducting the magnetic Reynolds number is much less then unity and hence the induced magnetic field can be neglected in comparison with the applied magnetic field in the absence of any input electric field ,the flow is governed by the following equations:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
The initial and boundary conditions for the velocity, temperature and concentration field are
![]() for all
for all ![]()
![]() at
at ![]()
![]() as
as ![]() (4)
(4)
Where ![]() is the velocity of the fluid along the plate in the
is the velocity of the fluid along the plate in the ![]() -directions,
-directions, ![]() is the time , g is the acceleration due to gravity, β is the coefficient of volume expansion,
is the time , g is the acceleration due to gravity, β is the coefficient of volume expansion, ![]() is the coefficient of thermal expansion with concentration,
is the coefficient of thermal expansion with concentration, ![]() is the temperature of the fluid near the plate,
is the temperature of the fluid near the plate, ![]() is the temperature of the fluid far away from the plate,
is the temperature of the fluid far away from the plate, ![]() is the temperature of the fluid.
is the temperature of the fluid. ![]() is the species concentration in the fluid,
is the species concentration in the fluid, ![]() is the species concentration in the fluid far away from the plate,
is the species concentration in the fluid far away from the plate, ![]() is the mass flux per unit area at the plate,
is the mass flux per unit area at the plate, ![]() is the kinematic viscosity,
is the kinematic viscosity, ![]() is the coefficient of kinematic visco-elastic parameter,
is the coefficient of kinematic visco-elastic parameter,![]() is the electrical conductivity of the fluid,
is the electrical conductivity of the fluid, ![]() is the magnetic permeability,
is the magnetic permeability,![]() is the strength of applied magnetic fluid,
is the strength of applied magnetic fluid, ![]() is the density of the fluid,
is the density of the fluid, ![]() is the specific heat at constant pressure,
is the specific heat at constant pressure, ![]() is the thermal conductivity of the fluid,
is the thermal conductivity of the fluid, ![]() is the viscosity of the fluid, D is the molecular diffusivity,
is the viscosity of the fluid, D is the molecular diffusivity, ![]() is the velocity of the plate.
is the velocity of the plate.
Equations (1) - (3) can be made dimensionless by introducing the following dimensionless variables and parameters:
In order to write the governing equations and boundary conditions in dimensionless from, the following non-dimensional quantities are introduced.
![]() (5)
(5)
![]()
![]()
Where Gr is the thermal Grashof number, Gc is modified Grashof number, Pr is prandtl number, M is the magnetic field parameter, Sc is Schmidt number, Kr is chemical reaction parameter, k is porous permeability, Q is heat sink parameter and S0 is the Soret number.
In terms of the above dimensionless quantities, Equations (1)-(3) reduces to
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
The corresponding boundary conditions are
![]() for all y ,t ≤ 0
for all y ,t ≤ 0
![]() at y=0 (9)
at y=0 (9)
![]() as
as ![]()
3. Solution of the Problem
Equations (6)-(8) are coupled, non-linear partial differential equations and these cannot be solved in closed –form using the initial and boundary conditions (9). However, these equations can be reduced to a set of ordinary differential equations, which can be solved analytically. This can be done by representing the velocity, temperature and concentration of the fluid in the neighborhood of the fluid in the neighborhood of the plate as
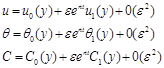 (10)
(10)
Substituting (10) in Equation (6)-(8) and equating the harmonic and non-harmonic terms, and neglecting the higher order terms of 0(![]() ),we obtain
),we obtain
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
The corresponding boundary conditions can be written as![]() at y=0
at y=0
![]() as (17)
as (17)
The equations (11) - (16) are still coupled and non – linear, whose exact solutions are not possible. So we expand ![]() in terms
in terms ![]() of Ec in the following form as the Eckert number is very small for incompressible flows.
of Ec in the following form as the Eckert number is very small for incompressible flows.
![]()
![]()
![]()
![]() (18)
(18)
Substituting (18) in Equations (11) – (16), equating the coefficients of Ec to Zero and neglecting the terms in ![]() and higher order, we get the following equations.
and higher order, we get the following equations.
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
![]() (26)
(26)
![]() (27)
(27)
![]() (28)
(28)
![]() (29)
(29)
![]() (30)
(30)
The respective boundary conditions are
![]() at y=0
at y=0
at (31)
![]() at y=0
at y=0
as (32)
Solving equations (19) –(30) under the boundary conditions (31) and (32) we obtain the velocity, temperature and concentration distributions in the boundary layer as
![]()
![]()
![]()
3.1. Skin-Friction
We now calculate Skin-friction from the velocity field; it is given in non-dimensional form as:
![]() ,
,
![]()
3.2. Rate of Heat Transfer
The dimensionless rate of heat transfer is given by
![]()
![]()
3.3. Rate of Mass Transfer
The dimensionless Sherwood number is given by
![]()
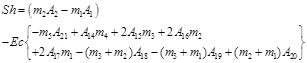
4. Results and Discussion
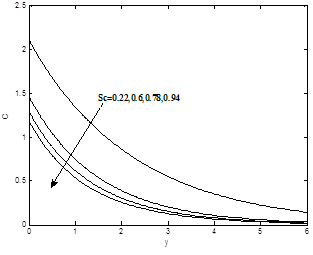
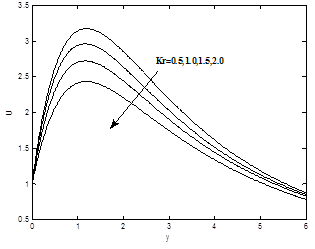
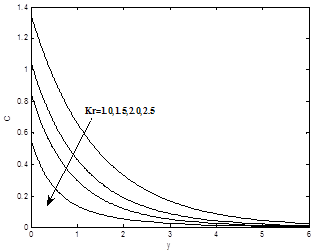
To analyze the results, Analytical computation has been carried out using the method described in the previous paragraph for various governing parameters, namely, thermal Grashof number Gr, modified Grashof number Gc, the magnetic field parameter M, permeability parameter K, Prandtl number Pr, Heat sink Q, Eckert number Ec, Schmidt number Sc, Soret number S0 and chemical reaction parameter Kr. In the present study the following default parameter values are adopted for computation: Gr=10, Gc=5, k=1.0, M=1.0, l=0.1, Pr=0.71, n=0.1, t=1.0, Sc=0.6, Ec=0.001, Q=0.5, S0=1.0, Kr=1.0, ε =0.01. All graphs therefore correspond to these values unless specifically indicated on the appropriate graph.
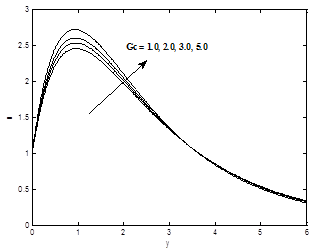
The variation of the thermal Grashof number Gr on the velocity profiles is presented in Figure 1 .It is observed that there is a rise in the velocity due to enhancement of thermal buoyancy force. Figure 2 presents typical velocity profiles in the boundary layer for various values of the solute Grashof number Gc, while all other parameters are kept at some fixed values. As expected, the fluid velocity increases as Solutal Grashof number Gc increase.
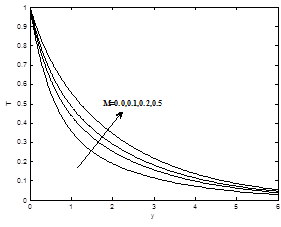
The effects of the magnetic field parameter M on the dimensionless velocity, dimensionless temperature and dimensionless concentration profiles are shown in the Figures 3(a) – 3(b). It is now a well established fact that the magnetic field presents a damping effect on the velocity field by creating drag force that opposes the fluid motion, causing the velocity to decrease for increasing values of magnetic field parameter M whereas temperature and concentration profiles increases as magnetic field parameter M increase.
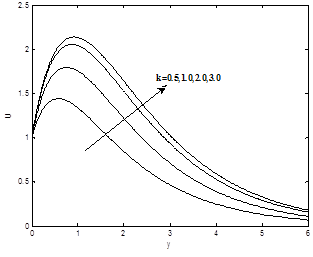
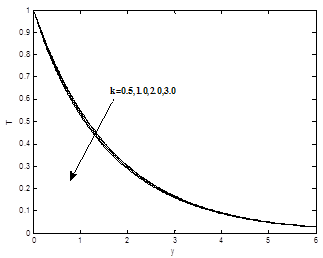
Figures 4(a) – 4(c) show the dimensionless velocity, dimensionless temperature and dimensionless concentration profiles for different values of permeability parameter K. It is noticed that as permeability of porous parameter k increases, the velocity profiles increase, the temperature and concentration profiles are decrease.
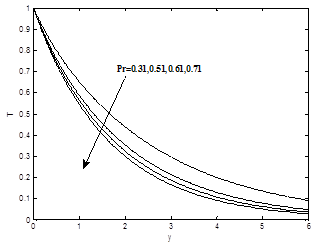
The influence of the Prandlt number Pr on velocity profiles is shown in Figure 5(a). It is obvious that velocity decrease as Prandlt number Pr increases. The influence of Prandtl number Pr on temperature field is shown in Figure 5(b).It is observed that temperature decrease as Prandtl parameter Pr increase.
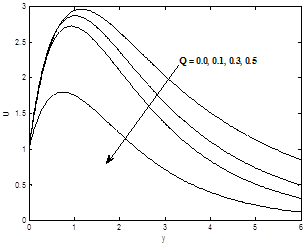
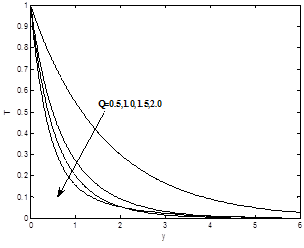
Figures 6(a) and 6(b) show the dimensionless velocity and the temperature profiles for different values of Heat absorption parameter Q. It can be seen that both velocity and temperature profiles decreases as heat absorption parameter Q increase.
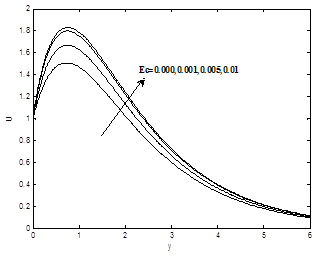
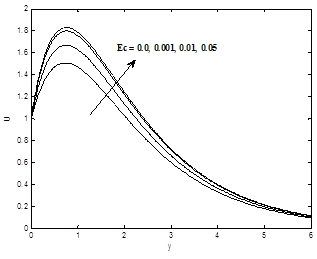
Figures 7(a) and 7(b) depict the effect of Eckert number Ec on the dimensionless velocity and temperature profiles .It is revealed that velocity scores grow with the increasing of the Eckert number Ec. Eckert number, physically is a measure of frictional heat in the system. Hence the thermal regime with large Ec values is subjected to rather more frictional heating causing a source of rise in the temperature. To be specific, Eckert number Ec signifies the relative importance of viscous heating to thermal diffusion, viscous heating may serve as energy source to modify the temperature regime qualitatively. Hence velocity and temperature profiles increase as Eckert number increase.
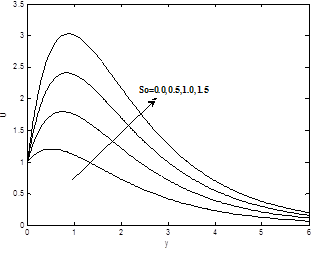
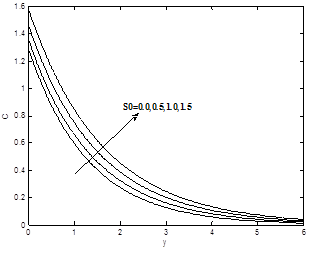
Figures 8(a) and 8(b) show the dimensionless velocity and concentration profiles for different values of soret number So. It can be seen that the velocity and concentration profiles increases with the increase of soret number So.
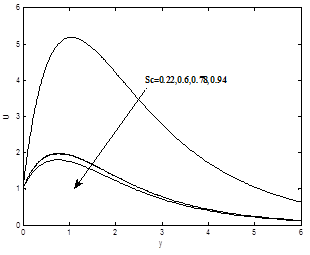
The influence of the Schmidt number Sc on the dimensionless velocity and concentration profiles are plotted in Figs. 9(a) and 9(b) respectively. As the Schmidt number increases the concentration decreases. This causes the concentration buoyancy effects to decrease yielding a reduction in the fluid velocity. The reductions in the velocity and concentration profiles are accompanied by simultaneous reductions in the velocity and concentration boundary layers. These behaviors are clear from Figs. 8(a) and 8(b).
Figure 10(a) and 10(b) show the dimensionless velocity and concentration profiles for different values of chemical reaction Kr. It can be seen that both velocity and the concentration profiles decrease with the increase of chemical reaction Kr.
|
|
|
| Fig 1. Variation of velocity profiles for different values of Gr | Fig 2. Variation of velocity profiles for different values of Gc |
|
|
|
| Fig 3(a). Variation of velocity profiles for different values of M | Fig 3(b). Variation of Temperature profiles for different values of M |
|
|
|
| Fig 3(c). Variation of Concentration profiles for different values of M | Fig 4(a). Variation of velocity profiles for different values of k |
|
|
|
| Fig 4(b). Variation of Temperature profiles for different values of k | Fig 4(c). Variation of Concentration profiles for different values of k |
|
|
|
| Fig 5(a). Variation of velocity profiles for different values of Pr | Fig 5(b). Variation of Temperature profiles for different values of Pr |
|
|
|
| Fig 6(a). Variation of velocity profiles for different values of Q | Fig 6(b). Variation of Temperature profiles for different values of Q |
|
|
|
| Fig 7(a). Variation of velocity profiles for different values of Ec | Fig 7(b). Variation of Temperature profiles for different values of Ec |
|
|
|
| Fig 8(a). Variation of velocity profiles for different values of S0 | Fig 8(b). Variation of Concentration profiles for different values of S0 |
|
|
|
| Fig 9(a). Variation of velocity profiles for different values of Sc | Fig 9(b). Variation of Concentration profiles for different values of Sc |
|
|
|
| Fig 10(a). Variation of velocity profiles for different values of Kr | Fig 10(b). Variation of Concentration profiles for different values Kr |
Appendix
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
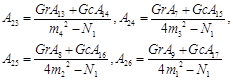
![]()
![]()
References
- O. Hassager. in: Working group on numerical techniques, in: Proceedings of the fifth workshop on numerical methods in non-newtonian flow. J. Non-Newton. Fluid Mech. 1988, 29, 2-5.
- M.F. Tomé; A. Castelo; V.G. Ferreira; S. McKee. J. Non-Newtonian Fluid Mech. 2008, 154, 179–206.
- K. R. Rajagopal, T. Y. Na and A. S. Gupta, "Flow of Visco-Elastic Fluid over a Stretching Sheet," Rheol Acta, Vol. 23, 1984, pp. 213-215.
- B. Siddappa and S. Abel, "Non-Newtonian flow past a stretching plate," Zeitschrift für Angewandte Mathematik und Physik (ZAMP), Vol. 36, 1985, pp. 890-892.
- T.G Cowling (1957), Magnet hydrodynamics, Wiley Inter Science, New York.
- K.P Crammer and S.I Pai (1973), Magneto fluid dynamics for engineering and applied physics, McGraw – Hill Book Co, New York.
- C C Chang and J.T Yen (1961), Magnetohydrodynamic channel flow under time dependent pressure gradient, Phys. Fluids, Vol 4, 1355 – 1361.
- M.K Mazumdar and R.K Deka (2007), MHD flow past an impulsively started infinite vertical plate in presence of thermal radiation, Romanian Journal of Physics, Vol. 52, No. 5 – 6, pp. 529 -535.
- M.K Chowdhury and M.N Islam, (2000) MHD free convection flow of visco-elastic fluid past an infinite vertical porous plate, Heat and Mass Transfer, Vol. 36, pp. 439-447.
- G Astarita (1967), Mass transfer with Chemical reaction, Elsevier Publishing Company, Amsterdam.
- A Apelblat (1982), Mass transfer with a chemical reaction of the first order effect of axial diffusion, The Chemical Engineering Journal, Vol. 23, No. 2, pp. 93 – 103.
- R Saravana., S Sreekanth., S Sreenadh and R Hemadri Reddy (2011), Mass transfer effects on MHD viscous flow past an impulsively started infinite vertical plate with constant mass flux, Advances in Applied Science Research, Vol. 2, No.1, pp. 221 – 229.
- G.C Dash., P.K Rath, N Mohapatra and P.K Dash (2009), Free convective MHD flow through porous media of a rotating visco-elastic fluid past an infinite vertical porous plate with heat and mass transfer in presence of chemical reaction, AMSE Model B, Vol. 78, No. 4, pp. 21-37.
- S.M. Alharbi, Mohamed A. A. Bazid, Mahmoud S. El Gendy, Heat and mass transfer in MHD viscoelastic fluid flow through a porous medium over a stretching sheet with chemical reaction, Applied Mathematics, Vol. 1, pp. 446-455.
- R Sivaraj and B Rushi Kumar (2013), Chemically reacting dusty viscoelastic fluid flow in an irregular channel with convective boundary. Ain Shams Engineering Journal 4, 93-101.
- Das, U.N., R.K. Deka, and V.M. Soundalgekar (1994). Effects of mass transfer on flow past an impulsively started infinite vertical plate with constant heat flux and chemical reaction. Forsch. Ingenieurwes 60, 284-287.
- Bodasa, G. and Borkakati, A. K.: Bulletin of Pure and Applied Sciences. Vol. 21E (No. 2); p. 451-460, (2002).
- Abo-Eladahab Emad M, El-Aziz Mohamed A. Blowing/suction effect on hydromagnetic heat transfer by mixed convection from an inclined continuously stretching surface with internal heat generation/absorption. Int. J. Therm. Sci 2004, 43, 709-719.
- Bataller R.C, Effects of heat source/sink, radiation and work done by deformation on the flow and heat transfer of a viscoelastic fluid over a stretching sheet. Comput Math Appl 2007, 53, 305-316.
- Abel M.S and Nandeppanavar Mahantesh M, Heat transfer in MHD viscoelastic boundary layer flow over a stretching sheet with non-uniform heat source/sink. Commun Nonlinear Sci Numer Simul 2009, 14, 120-131.
- Vajravelu, K and. Hadyinicolaou, A Convective heat transfer in an electrically conducting fluid at a stretching surface with uniform free stream, Internat. J. Engng. Science, Vol. 35, No. 12-13, pp. 1237-1244, 1997.
- M Umamaheswar., S.V.K Varma and M.C Raju (2013), Unsteady MHD free convective visco-elastic fluid flow bounded by an infinite inclined porous plate inn presence of heat source, viscous dissipation and ohmic heating, International Journal of Advanced Science and Technology, Vol. 61, pp. 39 – 52.
- Kinyanjuli., J.K Kwanza and S.M Uppal (2001), Magneto hydrodynamic free convection heat and mass transfer of a heat generating fluid past an impulsively started infinite vertical porous plate with hall current and radiation absorption, Energy Conversion and Management, Vol. 42, No. 8, pp. 917 – 931.
- B.I Olajuwon and J.I Oahimire,(2014) Effect of thermal diffusion and chemical reaction on heat and mass transfer in an MHD micropolar fluid with heat generation. Afrika Matematika 25, 911-931.
- M Bhavana., D Chenna Kesavaiah and A Sudhakaraiah ( 2013), The Soret effect on free convective unsteady MHD flow over a vertical plate with heat source, Int. J. of Innovative Research in Science, Engineering and Technology, Vol. 2. No. 5, pp. 1617 – 1628.
- K Choudhary and A Sharma (2014), Influence of soret effect on MHD mixed convection flow of visco-elastic fluid past a vertical surface with hall effect, Int. J. of Applied Mechanics and Engineering, 2014, vol.19, No.1, pp.79-95.
- N Ahmed (2012), Heat and mass transfer in Hartman flow with Soret effect in presence of a constant heat source, Turkish J of Phy, Vol 33, pp. 446 – 460.
- N Ahmed (2012) Soret and radiation effects on transient MHD free convection from an impulsively started infinite vertical plate, Journal of Heat Transfer (ASME), Vol. 134, pp. 1 – 9.
- M Turkyilmazoglu and I Pop (2012), Soret and heat source effects on the unsteady radiative MHD free convection flow from an impulsively started infinite vertical plate, International Journal of Heat and Mass Transfer, Vol. 55, No. 25-26, pp. 7635-7644.