Ontology Similarity Measuring and Ontology Mapping Algorithms Based on Majorization-Minimization Method
Yun Gao1, *, Wei Gao2
1Department of Editorial, Yunnan Normal University, Kunming, China
2School of Information Science and Technology, Yunnan Normal University, Kunming, China
Abstract
Ontology similarity calculation is important research topics in information retrieval and widely used in science and engineering. In information retrieval, ontology is aiming to find the highly semantic similarity information of the original query concept, and then return the results to the user. Ontology mapping is aiming toconstruct the relationship between two or more ontologies. The core trick of ontology applications is to calculate the similarity between the vertices in the ontology graph. By analyzing the technology of majorization-minimization, we propose the new algorithm for ontology similarity measure and ontology mapping. Via the ontology sparse vector learning, the ontology graph is mapped into a line consists of real numbers. The similarity between two concepts then can be measured by comparing the difference between their corresponding real numbers. The experiment results show that the proposed new algorithm has high accuracy and efficiency on ontology similarity calculation and ontology mapping in biology and physics applications.
Keywords
Ontology, Similarity Measure, Ontology Mapping, Sparse Vector, Majorization-Minimization
Received: April 4, 2015
Accepted: April 24, 2015
Published online: May 28, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
Asa conceptual shared and knowledge representation model, ontologyhas been used in knowledge management, image retrieval and information retrieval search extension. Furthermore, acted as an effective concept semantic model, ontology is employed in other fields except computer science, including medical science, social science,pharmacology science, geography science and biology scienceRef. input by wrong way?(see Przydzial et al., [1], Koehler et al., [2], Ivanovic and Budimac[3], Hristoskova et al., [4], and Kabir et al., [5] for more detail).
The ontology model is a graph G=(V,E) such that each vertex vexpresses a concept and each directed edge e=vivjdenote a relationship between concepts vi and vj. Theaim of ontology similarity measure is to get a similarity function Sim: V×V ![]()
![]()
![]() {0} such that each pair of vertices is mapped to a non-negative real number.Moreover, the aim of ontology mapping is to obtain the link between two or more ontologies. In more applications, the keyof ontology mapping is to get a similarity function Sto determine the similarity between vertices from different ontologies.
{0} such that each pair of vertices is mapped to a non-negative real number.Moreover, the aim of ontology mapping is to obtain the link between two or more ontologies. In more applications, the keyof ontology mapping is to get a similarity function Sto determine the similarity between vertices from different ontologies.
In recent years, ontology similarity-based technologies were employed in many applications. By virtue of technology for stable semantic measurement, a graph derivation representation based trick for stable semantic measurement is presented by Ma et al., [6]. Li et al., [7] determined an ontology representation method which can be used in online shopping customer knowledge with enterprise information. A creative ontology matching system is proposed by Santodomingo et al., [8] such thatthe complex correspondences are deduced by processing expert knowledge with external domain ontologies and in view of novel matching technologies. The main features of the food ontology and several examples of application for traceability aims is reported by Pizzuti et al., [9]. Lasierra et al., [10]pointed out that ontologies can be employed in designing an architecture for taking care of patients at home. More ontology learning algorithms can refer to [11-22].
In this paper, we present the new ontology similarity computation and ontology mapping algorithms relied on sparse vector learning andmajorization-minimizationmethod or Technology. In terms of thesparse vector, the ontology graph is mapped into a real line and vertices are mapped into real numbers. Then the similarity between vertices is measured by the difference between their corresponding real numbers.
2. Basic Idea
Let V be an instance space and ![]() be a n dimensional vector space.For any vertex in ontology graph G, its information (including its attribute, instance, structure, name and semantic information of the concept which iscorresponding to the vertex and that is contained in its vector)is denoted by a vector with p dimension. Let v=
be a n dimensional vector space.For any vertex in ontology graph G, its information (including its attribute, instance, structure, name and semantic information of the concept which iscorresponding to the vertex and that is contained in its vector)is denoted by a vector with p dimension. Let v=![]() be a vector which is corresponding to a vertex v. For facilitating theexpression, we slightly confuse the notations and denotev both the ontology vertex and its corresponding vector.The purpose of ontology learning algorithmsis toget an optimal ontology function f: V
be a vector which is corresponding to a vertex v. For facilitating theexpression, we slightly confuse the notations and denotev both the ontology vertex and its corresponding vector.The purpose of ontology learning algorithmsis toget an optimal ontology function f: V![]()
![]() , then the similarity between two vertices is determined by the difference between two real numbers which they correspond to.Theessence of such algorithmis dimensionality reduction, that is to say, use one dimension vector to represent p dimension vector. From this point of view, an ontology function f can be regarded as a dimensionality reduction map as f:
, then the similarity between two vertices is determined by the difference between two real numbers which they correspond to.Theessence of such algorithmis dimensionality reduction, that is to say, use one dimension vector to represent p dimension vector. From this point of view, an ontology function f can be regarded as a dimensionality reduction map as f: ![]()
![]()
![]() .
.
In the real implement, thesparse ontology functioncan be denotedas
![]() =
=![]() , (1)
, (1)
where ![]() =
=![]() is a sparse vector. For determining the ontology function f, we should get the sparse vector
is a sparse vector. For determining the ontology function f, we should get the sparse vector ![]() first.
first.
3. Main Ontology Algorithms
In this section, it willpresent our main ontology sparse vector learning algorithms for ontology similarity measuring and ontology mapping by virtue ofmajorization-minimization trick.
The ontology sparse vector learning model using fused lasso regression (FLR)was defined by
![]()
![]() , (2)
, (2)
where y![]()
![]() is the response vector, and V
is the response vector, and V![]()
![]() is the ontology matrix; n is the sample number,
is the ontology matrix; n is the sample number, ![]() and
and ![]() are non-negative regularization parameters,and E is the unordered index set of the adjacent pairs of variables specified in the model.
are non-negative regularization parameters,and E is the unordered index set of the adjacent pairs of variables specified in the model.
In thispaper,it will use an MM trick to solve the ontology problem (2). Given the current estimate ![]() of the optimal solution to ontology problem (2), the majorization step finds a majorizing function
of the optimal solution to ontology problem (2), the majorization step finds a majorizing function![]() such that
such that![]() =
= ![]() and
and ![]()
![]()
![]() for
for![]() . The minimizationstep updates the estimate with
. The minimizationstep updates the estimate with
![]() =
=![]() .
.
It has a descent character that![]()
![]()
![]() . Furthermore, if
. Furthermore, if ![]() meets some regularity conditions, the MM produce converges to the optimal solution of
meets some regularity conditions, the MM produce converges to the optimal solution of![]() .
.
The MM technology has been applied to the classical lasso problem such that it propose to minimize a perturbed version of the objective function of theclassical lasso
![]()
![]()
instead of
![]()
to avoid division by zero in the learning. The majorizing function for![]() at
at ![]() is obtained by
is obtained by
![]() =
=![]()
![]() .
.
The sequence ![]() with
with ![]() =
=![]() converges to the minimizer of
converges to the minimizer of![]() , and
, and ![]() converges to
converges to![]() uniformly as
uniformly as ![]() tends to 0.
tends to 0.
Introducing a perturbed version ![]() of the objective (2) and then the majorizing function
of the objective (2) and then the majorizing function ![]() for the ontology problem (2):
for the ontology problem (2):
![]()
![]()
![]() , (3)
, (3)
and
![]() =
=![]()
![]()
![]()
![]() . (4)
. (4)
Since ![]() is a smooth convex function on
is a smooth convex function on![]() , we have that
, we have that ![]() majorizes
majorizes![]() at
at ![]() and has a unique global minimum on the rank of V.
and has a unique global minimum on the rank of V.
Now, let ![]() be the current estimate in the r-th iteration. The majorizing function
be the current estimate in the r-th iteration. The majorizing function![]() is minimized over
is minimized over ![]() if
if ![]() =0, and can be expressed as a linearsystem of equations
=0, and can be expressed as a linearsystem of equations
![]() =
=![]() , (5)
, (5)
where ![]() =
=![]() with
with ![]() =
=![]() for
for ![]() and
and ![]() =
= ![]() is a symmetric and positive semidefinite matrix with
is a symmetric and positive semidefinite matrix with
![]() =
=![]() ,
,![]() ,
,
![]() =
=![]() =
=![]() ,
, ![]() .
.
The procedure presented as Algorithm 1 below.
Algorithm 1. FLR based on MM method.
Input: y, V, ![]() ,
, ![]() , convergence tolerance
, convergence tolerance ![]() , perturbation constant
, perturbation constant ![]() .
.
Step 1: for j=1,…,p do
Step 2:![]()
![]()
![]()
Step 3: end for
Step 4: repeat r=0,1,2,…
Step 5: ![]()
![]()
![]()
Step 6: ![]()
![]()
![]()
Step 7: until ![]()
![]()
![]()
Output: ![]() =
=![]() .
.
If ![]() is tridiagonal or blocktridiagonal, we can use the preconditioned conjugategradient (PCG) trick by using the matrix
is tridiagonal or blocktridiagonal, we can use the preconditioned conjugategradient (PCG) trick by using the matrix ![]() as the preconditioner to efficiently determine the linear system (5). The PCG technology is an iterative trick for solving a linear system
as the preconditioner to efficiently determine the linear system (5). The PCG technology is an iterative trick for solving a linear system![]() =c, where Q is a symmetric positive definite matrix and Mis a preconditioner matrix. For instance, we can use M=
=c, where Q is a symmetric positive definite matrix and Mis a preconditioner matrix. For instance, we can use M=![]() for Q=
for Q=![]() . The PCG methoddeduces the solution via iteratively updating four sequences
. The PCG methoddeduces the solution via iteratively updating four sequences ![]() ,
, ![]() ,
, ![]() , and
, and![]() with
with
![]() =
=![]() ,
,
![]() =
=![]() ,
,
![]() =
=![]() ,
,
![]() =
=![]() ,
,
where![]() =
=![]() ,
, ![]() =
=![]() ,
, ![]() ,
, ![]() =c,
=c, ![]() =
=![]() ,and
,and ![]() =
=![]() . For the standard FLR ontology model, we can solve the linear system
. For the standard FLR ontology model, we can solve the linear system ![]() =
=![]() using LAPACK functions dpbtrf and dpbtrs. Algorithm 2 manifests the proposedMM based ontology algorithm using the PCG method under the standard FLR framework.
using LAPACK functions dpbtrf and dpbtrs. Algorithm 2 manifests the proposedMM based ontology algorithm using the PCG method under the standard FLR framework.
Algorithm 2.MM based ontology algorithm using the PCG method for the standard FLR and the two-dimensional FLR framework
Input: y, V, ![]() ,
,![]() , convergence tolerance
, convergence tolerance ![]() , perturbation constant
, perturbation constant ![]() .
.
Step 1: for j=1,…,p do
Step 2:![]()
![]()
![]()
Step 3: end for
Step 4: repeat r=0,1,2,…
Step 5: ![]()
![]()
![]()
Step 6: ![]()
![]()
![]()
Step 7: ![]()
![]()
![]()
Step 8: ![]()
![]()
![]()
Step 9: ![]()
![]()
![]()
Step 10: repeat j=1,2,…
Step 11: ![]()
![]()
![]()
Step 12: ![]()
![]()
![]()
Step 13: ![]()
![]()
![]()
Step 14: Solve ![]()
Step 15: ![]()
![]()
![]()
Step 16: ![]()
![]()
![]()
Step 17: until ![]()
![]()
![]()
Step 18: ![]()
![]()
![]()
Step 19: until ![]()
![]()
![]()
Output: ![]() =
=![]() .
.
4. Experiments
Two simulation experiments on ontology similarity measure and ontology mapping are designed in this section.For detail implement, onefirst obtain the optimal sparse vector using the algorithm raised in our paper, and then the ontology function is yielded by (1).
4.1. Experiment on Biology Data
The "Go" ontology O1 was constructed byhttp: //www. geneontology. org. (Fig. 1 presents the graph structure of O1). We use P@N (defined by Craswell and Hawking [23]) to determine the equality of the experiment result.
Beside our ontology algorithm, ontology algorithms in Huang et al., [12], Gao and Liang [13] and Gao and Gao[14] are also acted to "Go" ontology. Then, we compare the precision ratio which we have deducedfrom the four tricks. Some parts of experiment results can be seen in Table 1.
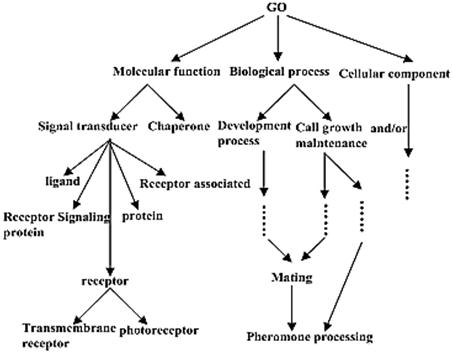
Figure 1. "Go" ontology
Table 1. The experiment data for ontology similarity measure
| P@3 average precision ratio | P@5 average precision ratio | P@10 average precision ratio | P@20 average precision ratio | |
| Simulation or experiment Algorithm | 47.08% | 53.92% | 63.78% | 81.69% |
| Algorithmin [12] | 46.38% | 53.48% | 62.34% | 74.59% |
| Algorithm in [13] | 43.56% | 49.38% | 56.47% | 71.94% |
| Algorithm in[14] | 42.13% | 51.83% | 60.19% | 72.39% |
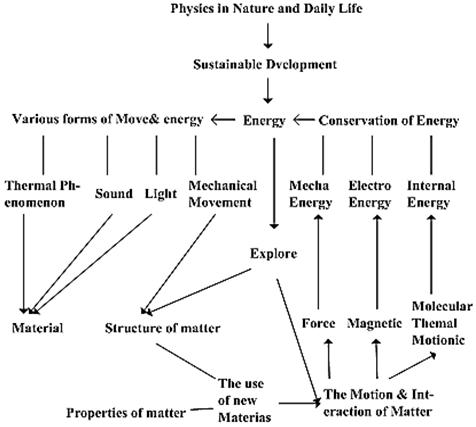
Figure 2. "Physical Education" Ontology O2
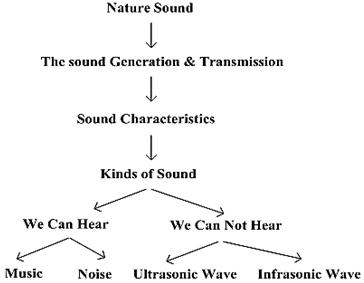
Figure 3. "Physical Education" Ontology O3.
As we can see in the Figure 1, when N= 3, 5, 10 or 20, the precision ratio in view of our algorithmis higher than that got by trickswhich has been determinedin Huang et al., [12], Gao and Liang [13] and Gao and Gao[14].
4.2. Experiment on Physical Education Data
For the second experiment, we use physical education ontologies O2 and O3 (the graph structures of O2 and O3 are raised in Fig. 2 and Fig. 3 respectively). The purpose of this experiment is to construct the ontology mapping between O2 and O3. Again, P@N criterion is applied to measure the equality of the experiment results.
Furthermore, ontology technologiesrefer to Huang et al., [12], Gao and Liang [13] and Gao et al., [16] are employed to "physical education" ontology. At last, we compare the precision ratio that we have obtained from four tricks. Table 2 present several resultsfor this experiment.
From what we have obtained in Table 2, we find itmore efficient to use our Algorithmthan algorithms determinedbyHuang et al., [12], Gao and Liang [13] and Gao et al., [16],especially whereN is sufficiently large.
Table 2. The experiment data for ontology mapping
| P@1 average precision ratio | P@3 average precision ratio | P@5 average precision ratio | |
| Algorithm | 69.13% | 80.65% | 92.26% |
| Algorithm in [12] | 61.29% | 73.12% | 79.35% |
| Algorithm in [13] | 69.13% | 75.56% | 84.52% |
| Algorithm in [16] | 67.74% | 77.42% | 89.68% |
5. Conclusions
In this article, a new algorithmfor ontology similarity measure and ontology mapping application is presented by virtue ofmajorization-minimization method. Furthermore, experiment resultsreveal that our new algorithm has high efficiency in both biology and physics education. The ontology algorithmpresented in our paper illustrates the promising application prospects forontology use.
Acknowledgment
We thank the reviewers for their constructive comments in improving the quality of this paper.The research is financed by: NSFC (No.11401519).
References
- J. M. Przydzial,B.Bhhatarai, and A. Koleti, GPCR ontology: development and application of a G protein-coupled receptor pharmacology knowledge framework. Bioinformatics, 29(24)(2013) 3211-3219.
- S.Koehler, S. C.Doelken, and C. J. Mungall, The human phenotype ontology project: linking molecular biology and disease through phenotype data. Nucleic Acids Research, 42(D1)(2014)966-974.
- M.Ivanovicand Z.Budimac, An overview of ontologies and data resources in medical domains. Expert Systerms and Applications, 41(11)(2014) 5158-15166.
- A.Hristoskova, V.Sakkalis, andG.Zacharioudakis,Ontology-driven monitoring of patient's vital signs enabling personalized medical detection and alert. Sensors, 14(1)(2014)1598-1628.
- M. A.Kabir, J.Han, and J.Yu, User-centric social context information management: an ontology-based approach and platform. Personal and Ubiquitous Computing, 18(3)(2014) 1061-1083.
- Y. L.Ma, L.Liu,K.Lu, B. H.Jin, andX. J.Liu, A graph derivation based approach for measuring and comparing structural semantics of ontologies. IEEE Transactions on Knowledge and Data Engineering, 26(3)(2014) 1039-1052.
- Z.Li, H. S.Guo, Y. S.Yuan, andL. B. Sun, Ontology representation of online shopping customers knowledge in enterprise information. Applied Mechanics and Materials, 483(2014) 603-606.
- R.Santodomingo, S., Rohjans, M.Uslar, J. A.Rodriguez-Mondejar, andM.A.Sanz-Bobi,Ontology matching system for future energy smart grids. Engineering Applications of Artificial Intelligence, 32(2014) 242-257.
- T.Pizzuti,G.Mirabelli,M. A.Sanz-Bobi, and F.Gomez-Gonzalez,Food Track & Trace ontology for helping the food traceability control. Journal of Food Engineering, 120(1)(2014) 17-30.
- N.Lasierra, A.Alesanco, and J.Garcia,Designing an architecture for monitoring patients at home: Ontologies and web services for clinical and technical management integration. IEEE Journal of Biomedical and Health Informatics, 18(3)(2014)896-906.
- Y. Y.Wang, W. Gao, Y. G. Zhang, andY. Gao,Ontology similarity computation use ranking learning Method.The 3rd International Conference on Computational Intelligence and Industrial Application,Wuhan, China, 2010, pp.20-22.
- X.Huang,T. W. Xu, W.Gao, andZ. Y. Jia,Ontology similarity measure and ontology mapping via fast ranking method.International Journal of Applied Physics and Mathematics, 1(2011)54-59.
- W.Gao, andL.Liang,Ontology similarity measure by optimizing NDCG measure and application in physics education.Future Communication, Computing, Control and Management,142(2011)415-421.
- Y.Gao,and W.Gao,Ontology similarity measure and ontology mapping via learning optimization similarity function.International Journal of Machine Learning and Computing,2(2)(2012)107-112.
- X.Huang,T.W.Xu,W.Gao,andS.Gong,Ontology similarity measure and ontology mapping using half transductive ranking.In Proceedings of 2011 4th IEEE international conference on computer science and Information technology, Chengdu, China,2011, pp.571-574.
- W. Gao, Y.Gao, andL. Liang, Diffusion and harmonic analysis on hypergraph and application in ontology similarity measure and ontology mapping.Journal of Chemical and Pharmaceutical Research, 5(9)(2013) 592-598.
- W. Gao and L. Shi, Ontology similarity measure algorithm with operational cost and application in biology science.BioTechnology: An Indian Journal, 8(11)(2013) 1572-1577.
- W. GaoandT. W. Xu, Ontology similarity measuring and ontology mapping algorithm based on MEE criterion. Energy Education Science and Technology Part A: Energy Science and Research, 32(3)(2014) 3793-3806
- W.Gao,Y. Gao, andY. G. Zhang,Strong and weak stability of k-partite ranking algorithm.Information,15(11A)(2012)4585-4590.
- W.GaoandT. W. Xu, Stability analysis of learning algorithms for ontology similarity computation.Abstract and Applied Analysis, 2013, 9 pages, http://dx.doi.org/10.1155/2013/174802.
- W. Gao and L.L. Zhu, Gradient learning algorithms for ontology computing. Computational Intelligence and Neuroscience, 2014, 12 pages, http://dx.doi.org/10.1155/2014/438291.
- W.Gao,L. Yan, and L. Liang,Piecewisefunctionapproximationand vertexpartitioningschemes formulti-dividingontologyalgorithm in AUCcriterionsetting (I).International Journal of Computer Applications in Technology, 50 (3/4)(2014)226-231.
- N. Craswell andD.Hawking, Overview of the TREC 2003 web track. Proceeding of the Twelfth Text Retrieval Conference, Gaithersburg, Maryland, NIST Special Publication, 2003, pp. 78-92.



