Analysis of Cosmic Rays from Inter-Electronic Structure of the Electron-Revised Version

D. P. Nandedkar^*

Department of Electrical Engineering, Indian Institute of Technology, Bombay, Powai, Mumbai, India

Abstract

Here an analysis of cosmic rays from inter-electronic structure of the electron is reconsidered with respect to a previous paper by Nandedkar, where electromagnetic nature of cosmic rays is analyzed along with complex charge and complex mass of an electron. Here it is interesting to note that the moving mass of the electron inside and / on periphery of the electron has a velocity of 4.239(4) x 10⁸ m/ sc which is greater than velocity of light in free space. Thus a world of Tachyon (where particle velocity can exceed velocity of light in free space) exit inside and / on periphery of the electron. In this paper strength of magnetic flux density required for reversal of spin angular momentum is reconsidered with real part of complex charge, of the moving electron along periphery of the circle of electron having radius of 1.878(8) x 10^-15 m, illustrating spin of the electron diagrammatically. This electron radius of 1.878(8) x 10^-15 m called "reduced radius" is (2/3) times so called "classical radius" of electron. Distribution of complex charge and complex mass of the electron is confined to the circle of "reduced radius" of the electron. Strength of magnetic flux density required for reversal of spin angular momentum is 1.877 x 10¹⁴Wb / m². Sudden alternate reversals of magnetic flux densities in this case of equal to or greater than above value, generate continuous waves of cosmic rays of frequency ~ 1.795(6) x 10²² Hz by complex mass/ complex charge inter-electronic structure, which is reconsidered.

Keywords

Cosmic-Rays, Electron, Complex-Mass, Complex-Charge

Received:June 3, 2016
Accepted: June 21, 2016
Published online: August 5, 2016

@ 2016 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY license. http://creativecommons.org/licenses/by/4.0/

1. Introduction

Cosmic rays are extremely penetrating radiations/ charged particles, coming from where we do not know for certain as yet, but doubtless from regions far away from earth, and continually bombarding it on all sides with more or less of uniform intensity.

It is considered that the cosmic rays have terrestrial origin. As regards nature of charged particles of which cosmic rays are composed of, whether positive or negative, protons or electrons, study of the latitude effect on earth, by itself, gives no indication whatever; nor does it excludes the possibility of the presence of photons or neutrons, [1-7].

In a previous paper by Nandedkar [8], an analysis of cosmic rays from inter-electronic structure of the electron is considered, where electromagnetic nature of cosmic rays is analyzed along with complex charge and complex mass of an electron. Here it is interesting to note that the moving mass of the electron inside and / on periphery of the electron has a velocity of 4.239(4) x  m / sc which is greater than velocity of light in free space. Thus a world of Tachyon [9] (where particle velocity can exceed velocity of light in free space) exit inside and/ on periphery of the electron. In this paper strength of magnetic flux density required for reversal of spin angular momentum is reconsidered with real part of complex charge, of the moving electron along periphery of the circle of electron having radius of 1.878(8) x  m, illustrating spin of the electron diagrammatically. This electron radius of 1.878(8) x  m called "reduced radius" is (2/3) times so called "classical radius" of electron.  Distribution of complex charge and complex mass of the electron is confined to the circle of "reduced radius" of the electron. Strength of magnetic flux density required for reversal of spin angular momentum is  Wb/. Sudden alternate reversals of magnetic flux densities in this case of equal to or greater than above value, generate continuous waves of cosmic rays of frequency ~ 1.795(6) x  Hz by complex mass/ complex charge inter-electronic structure, which is reconsidered.

Frequencies higher than about  Hz of Electromagnetic Waves are classified in Cosmic Rays. In this research-paper, aspect of electromagnetic nature of the cosmic rays is re-considered in detail incorporating some additional data with reference to previous paper by Nandedkar [8].

Figures in this article are in, Plane of Paper for hard-copy version/ Plane of Flat Monitor of Computer for soft-copy version, unless otherwise specified.

The article is developed in following Sections:

1. Introduction

2. Radius of an Electron

3. Complex Charge and Complex mass of an Electron

4. Electromagnetic Radiation Generation by the Electron

5. Numerical Analysis and

6. Conclusions

2. Radius of an Electron

Let a small uniformly charged sphere O i.e. the electron of radius  and charge e moves along the X-axis with a steady velocity u. If this velocity is not large, it may be assumed that the sphere carriers its Faradays tubes along with it, undisturbed as the electromagnetic induction that tends to distort the tubes of force, depends on the velocity of motion - (Fig 1).

As the moving charge O is equivalent to a current i of strength i = eu, the magnetic field H due to it at a point P, distant r from O is given by Biot (Ampere) Law as follows,

                                                                        (1)

where  is the angle between r and X-axis. Therefore energy density w of magnetic field [10] at P, is given by,

                                                                        (2)

where is permeability of free space.

Now consider a small element PQRS at P (Fig. 1) with PQ = dr and PS subtending at O an angle , so that PS = r . The area of the element PQRS (in the plane of the Fig. 1) = r  x dr. Dropping a perpendicular PN = r  on the X-axis from P, if the small area PQRS considered above at P, be revolved about OX-axis then it will enclose a ring, every bit of which lies upon the circumference of the circle whose radius is PN = r and whose plane is perpendicular to OX and hence has the same value for H.

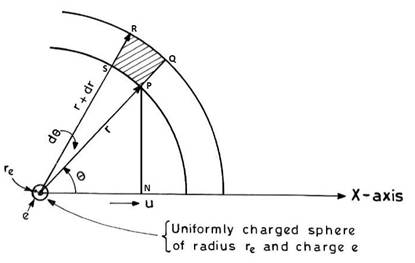
Fig. 1. Diagram for considering of magnetic field energy of a moving electron of finite size with velocity u along X-axis.

The volume of this ring is d, where

d= x d [

which gives,

d =                             (3)

The contribution to the differential energy of the magnetic field dw at d is given, using eqns. (1), (2) and (3), by

             (4)

Integrating (Fig. 1) the above quantity given by eqn. (4), for all values r i.e. from OP =  to ∞ (where  is the radius of electron), and for all values of q, i.e. from 0 to , total energy due to the moving charged sphere i.e. the electron, is given by,

W.        (5)

The above energy, is also the kinetic energy E of electron, given by,

                                     (6)

here  is rest mass of electron, assuming,

                                            (7)

where c is the velocity of an electromagnetic wave in free space.

Equating eqns. (5) and (6) gives,

= ,                                       (8)

here the mass  is due to motion where eqn. (7) holds good and, energy associated with the field is given by eqn. (6), in Newtonian World.

Now [10],

,                                        (9)

so,

= ,                                 (10)

using eqns. (8) and (9). Eqn. (10) gives radius of an electron. Here  is permittivity of free space. Now classical radius of electron  is given [11] by,

= .                             (11)

From eqns. (10) and (11),

/= 2/ 3.                            (12)

In view of eqn. (12),  of eqn. (10) is called "reduced radius" of the electron, whereas eqn. (11) gives "classical radius" of the electron. In this analysis "radius" word is used for "reduced radius" of the electron, unless otherwise specified.

3. Complex Charge and Complex Mass of an Electron

From eqn. (10),

.                              (13)

In eqn. (13),  is the total energy associated with rest ma-ss  of the electron [12]. Here  gives Potential E-nergy of either charges  or  due to  or separated by a distance  - (here also refer to Secn. 4), such that,

 +  = e,                                (14)

and,

 =                              (15)

The solution of simultaneous equations denoted by eqns. (14) and (15) in  and  gives that,

 = ,                         (16)

and,

 = ,                          (17)

where i = .

Let  be the rest mass of charge  and  be the rest mass of charge , such that total rest mass of charges and  is  =  and total rest mass energy of them is,

 = .            (18)

And then eqn. (13) can be rewritten as follows:

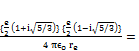{,(19)

where,  is rest mass of charge  = , and  is rest mass of charge  =  using eqns. (15), (16), (17) and (18).

4. Electromagnetic Radiation Generation by the Electron

Fig. 2. Complex charge and complex mass structure of electron of radius  in (p, ϕ)-plane of a system of polar co-ordinates. Here imaginary-axis is not shown in above Figure. Entities associated with a factor i =  are mathematical operators only.

In this model of electron, the charge  with rest mass is present at origin O of a system of polar co-ordinates (p, ϕ). And charge  rotate along circle of radius  with charge  hinged at O - (Fig. 2), forming a stable system, is the assumption. The plane of Fig. 2 is Plane of Paper.

Now potential energy of charge  on circumference of circle of radius  due to potential of charge  at O (Fig. 2) is    [refer to eqns. (13) and (15)]. Similarly potential energy of charge  at center O due to potential of charge  on circumference of circle of radius  (Fig. 2) is   [refer to eqns. (13) and (15)]. So this rest mass energy of the electron  is also effective pair potential energy that describes the interaction which acts along the line of length equal to the radius  of electron connecting the (two point) charges  and .

Let  be the moving mass of charge. Now the assumption is that, this charge of moving mass moves with uniform velocity v along the circumference of the circle of radius (Fig. 2). Then,

,                               (20)

by Einstein theory of relativity [12].

If I is the moment of Inertia of the spinning electron about O, then

I = .                                     (21)

And spinning energy associated with this charge  is then,

,                     (22)

where  is the angular velocity of the spinning/rotating electron in the circle of radius .

Further energy associated with moving charge of mass  by Einstein theory of relativity [12], is given as follows:

 = .                                  (23)

Here  of eqn. (22) and,  of eqn. (23) are same. Hence equating the two, the result is.

                                      (24)

But spin angular momentum of charge  is,

 = I = ,                             (25)

using eqn. (21).

Further, the spin angular momentum of the electron is considered to be given by,

,                                    (26)

where, ±1/2 is spin quantum number, say +1/2 for clockwise spin & -1/2 for anti-clockwise spin of the electron and, h is Plank constant, in analogy with Uhlenbeck and Goudschmidt (1925-1926) model of spinning electron [13]. Eqn. (26) is the assumption of this analysis.

From eqn. (26) choosing +1/2 spin quantum number, eqn. (25) gives,

.                            (27)

Substituting the value of from eqn. (24) in eqn. (27), eqn. (27) gives,

                             (28)

where,

ℏ = h/2p,                                    (29)

is reduced Planck constant.

Further, since

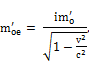
which is eqn. (20) and,

 c,                          (30)

using eqn. (24), hence eqn. (20) using eqn. (30), gives,

 =                           (31)

using eqn. (28).

Energy associated with spin angular momentum + (1/2)  [refer to eqn. (26) and eqn. (29)] is , say in clockwise spin of the electron [refer to eqn. (23)]. Similarly, energy associated with spin angular momentum  (1/2)  [refer to eqn. (26) and eqn. (29)] is - , say in anticlockwise spin of the electron [refer to eqn. (23)]. So change of energy of the electron when its spin momentum changes from + (1/2) to  (1/2)  is given by,

 ()] = 2 .          (32)

The above difference of energy of the electron is radiated with a photon of frequency n of energy hn, by Planck hypothesis. Whence Eqn. (32) gives,

hn = 2                                  (33)

Using eqn. (31), eqn. (33) gives,

n = .                                    (34)

Equation (34) gives frequency of electromagnetic radiation from the electron as its spin angular momentum changes from + (1/2) to  (1/2).

5. Numerical Analysis

Here numerical values of various entities with reference to previous paper by Nandedkar [8] are mentioned below (for ready reference), using "Data / Table 16/ General Physical Constants" of Appendix 9, pp. 1003 [14]:

[1]. Radius of the electron (:

=  = 1.878(8) x  m,        (35)

refer to eqn. (10).

[2]. Velocity of the electron ():

 c = 4.239(4) x  m/ sc,           (36)

refer to eqn. (30).

This velocity is greater than velocity of electromagnetic radiation in free space, which can happen in Tachyon world [9].

[3]. Angular velocity of the electron (:

 c/ = 2.256(4) x  rad/ sc,         (37)

refer to eqn. (30).

[4]. Moving mass of the electron (

 Kgm,      (38)

refer to eqn. (31).

[5]. Frequency of electromagnetic radiation from the electron (n):

n =  = 1.795(6) x  Hz            (39)

[refer to eqn. (34], which is due to reversal of spin momentum of the electron. n is in the range of cosmic rays.

[6]. Wavelength of electromagnetic radiation from the electron (

 =  =  = 1.669(5) x          (40)

[refer to eqn. (39)], which is due to reversal of spin momentum of the electron.  is in the range of cosmic rays.

[7]. Strength of magnetic field required for reversal of spin angular momentum (B):

Here, value of magnetic flux density due to circulation of complex electronic current giving Real part of current due to Real charge along positive Y-axis (Fig. 3) is carried out in following steps.

Now magnetic flux density B [where instantaneous position of the electron denoted by arbitrary point Q coincides with point A on the circular electronic path shown in Fig. 3] developed normal to and entering along negative Z-axis towards O and in the XY-plane of circular motion of the moving (say, clockwise) real charge  of Complex Charge (moving),  =  of eqn. (17) with velocity v of the electron which is in XY-plane of the paper, of the Fig. 3 produces Lorentz Force  (assumed to hold good) acting radially towards Centre O (Fig. 3) and along negative X-axis in XY-plane of paper of the Fig. 3, that is given by following relationship:

 = B  v.                              (41)

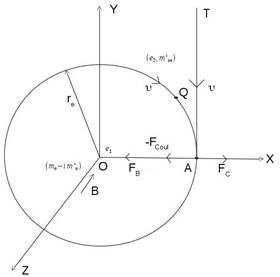
Fig. 3. Charge  = (e/2)  of electron rotating clockwise in a circle of electron radius  with moving mass  and velocity v in XY- plane, where imaginary-axis is not shown in above Figure. Entities associated with a factor i =  are mathematical operators only. Charge  = (e/2)  of electron with its rest mass  is at Center O of the circle of electron radius . Here B = magnetic flux density developed (due to circulation of Real part of current due to Real charge along positive Y-axis is assumption, acting along negative Z-axis towards O,  = Lorentz Force acting towards O along negative X-axis in XY-plane,  = Coulomb Force of Repulsion acting towards O along negative X-axis in XY-plane, and  = Centrifugal Force acting away from O along positive X-axis in XY-plane. Orientation of X-axis in XY-plane is to be chosen such that v is always instantaneously tangential to path of circular motion of electron in XY-plane (say at A) and OX is normal to v along the tangent TA at A. Here Q denotes an arbitrary point on circular orbit of the electron of Fig. 3. Origin O of the system of Polar co-ordinates (p, ϕ) with (p, ϕ) - plane of Fig. 2, is same as origin O of the system of Cartesian co-ordinates (X, Y) with (X, Y) – plane of Fig. 3. Plane of Fig. 2 is same as plane of Fig. 3, which is the plane of paper. Radius of electron  is same in circles of the radius  (Fig. 2 & Fig. 3) and Center O of Fig. 2 coincides with Center O of Fig. 3, although both Figures are drawn with different scales.

Whereas Coulomb Force  (assumed to hold good) of repulsion between Charge (stationary),  =  of eqn. (16) and Charge (moving),  =  of eqn. (17), separated by distance of  of electron radius of Fig. 3 [where instantaneous position of the electron denoted by arbitrary point Q coincides with point A on the circular electronic path shown in Fig. 3 as mentioned before], is given by Coulomb Law, viz.,

 = /,                (42)

where,

 = ,   (43)

and where  and  are given by eqns. (16) and (17) respectively, [here refer also to eqn. (15)]. And here  is given by eqn. (10). -  acts radially towards Centre O along negative X-axis in XY-plane of the paper of Fig. 3.

Thus a force due to difference of Lorentz and Coulomb forces, viz.,

 - ,                                (44)

acts towards Center O of circular path of electron of Fig. 3 along negative X-axis in XY-plane of the paper.

Further Centrifugal Force  (assumed to hold good) acting on the above electron in the XY-plane of the paper [where instantaneous position of the electron denoted by arbitrary point Q coincides with point A on the circular electronic path shown in Fig. 3 as mentioned before], and radially away from Centre O along positive X-axis due to circular motion of the electron, is given by,

 = ,                                (45)

where , v and  are given by eqns. (28), (30) and (10) respectively.

Expressions given by eqns. (44) and (45) are the same. Whence equating them gives,

 -  = .                              (46)

Eqn. (46) using eqns. (41), (42) and (45), gives,

B = 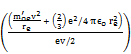 = 1.877(1) x  Wb/ (47)

6. Conclusions

An analysis of cosmic rays from inter-electronic structure of the electron is reconsidered with respect to a previous paper by Nandedkar [8], where electromagnetic nature of cosmic rays is analyzed along with complex charge and complex mass of an electron. Here it is interesting to note that the moving mass  Kgm of the electron [eqn. (38)] inside and/ on periphery of the electron has a velocity of 4.239(4) x  m/ sc [eqn. (36)] which is greater than velocity of light in free space. Thus a world of Tachyon [9] (where particle velocity can exceed velocity of light in free space) exit inside and/ on periphery of the electron. In this paper strength of magnetic flux density required for reversal of spin angular momentum is reconsidered with real part of complex charge, of the moving electron along periphery of the circle of electron having radius of 1.878(8) x  m [(eqn. (35)], illustrating spin of the electron diagrammatically (Fig. 3). This electron radius of 1.878(8) x  m called "reduced radius" is (2/3) times so called "classical radius" of electron [refer to eqns. (10, 11 & 12]. Distribution of complex charge and complex mass of the electron is confined to the circle of "reduced radius" of the electron (Fig. 2). Strength of magnetic flux density required for reversal of spin angular momentum is  Wb/ [eqn. (47)], as per (assumed) quantum condition of spin angular momentum  of eqn. (26). Sudden alternate reversals of magnetic flux densities in this case of equal to or greater than above value, generate continuous waves of cosmic rays of frequency ~ 1.795(6) x  Hz [eqn. (39)] by complex mass/ complex charge inter-electronic structure reconsidered herewith.

Here note that potential energy of charge  on circumference of circle of radius  due to potential of charge  at O (Fig. 2) is    [refer to eqns. (13) and (15)]. Similarly potential energy of charge  at center O due to potential of charge  on circumference of circle of radius  (Fig. 2) is   [refer to eqns. (13) and (15)]. So this rest mass energy of the electron  is also effective pair potential energy that describes the interaction which acts along the line of length equal to the radius  of electron connecting the (two point) charges  and .

This research-paper illustrates diagrammatically spin of electron [Fig. 2 and Fig. 3 which are assumed to hold good. Here the assumption is that, the charge of moving mass  {eqn. (31)} moves with uniform velocity v {eqn. (30)} along the circumference of the circle of radius {Fig. 2 and Fig. 3)}] with all entities associated therein with a factor i =  as mathematical operators only, in Tachyon world [9] for the electron of charge e and mass  of Newtonian world.

In this analysis Lorentz Force [eqn. (41)], Centrifugal Force [eqn. (45)] and Coulomb Force of Repulsion [eqn. (42)], are all assumed to hold good and are all Real. Balancing for moving electron (Fig. 3) under these Forces for inward Lorentz Force towards Center O of circle (Fig. 3) against outward Centrifugal Force & Coulomb Force of Repulsion with reference to stationary charge at Center O of circle of ‘reduced radius’ of electron away from Center O of circle (Fig. 3) considering say, instantaneous position of the electron denoted by arbitrary point Q coinciding with point A on the circular electronic path shown in Fig. 3, gives magnetic flux density as Real & positive required for reversal of spin angular momentum as given by eqn. (47) of value  Wb/.

If different species of electrons with different charge/ mass ratios and hence different radii be considered to exit in this vast universe, then a continuous/ desecrate band of cosmic rays of various frequencies may be generated, depending upon what different species of electrons with different charge/ mass ratios and hence different radii are available in this vast universe. Data on energy spectra of cosmic ray (photons) at Cosmic Ray Observatory corresponding to Wikipedia, the free encyclopaedia, can also considered to be due to production of cosmic rays mentioned in this article.

Acknowledgements

The author is thankful for the interesting discussions with reference to this research-paper given herewith he had, with his Guru (the Teacher) Dr. Ing. G. K. Bhagavat, [(now) Late] Professor of Electrical Engineering Department, Indian Institute of Technology (IIT), Bombay, Powai, Mumbai, India.

Further he gives thanks also to Electrical Engineering Department, IIT, Mumbai, India for giving permission to publish this research-work.

References

1. Michael A. DuVernois (Editor) (1999): "Topics in Cosmic-Ray Astrophysics", Nova Science Publishers Inc, USA.
2. Ringuet L. L., (1950): "Cosmic Rays", Prentice-Hall, New York.
3. A. Dauvillier, (1954): "Les Rayons Cosmiques", Dunod publisher, Paris, France.
4. Wilson J. G.-Editor, (1952): "Progress in cosmic ray physics", Vol. I, North Holland, Amsterdam.
5. Wilson J. G.-Editor, (1954): "Progress in cosmic ray physics", Vol. II, North Holland, Amsterdam.
6. Wilson J. G.-Editor, (1956): "Progress in cosmic ray physics", Vol. III, North Holland, Amsterdam.
7. Mewaldt, R. A., (1996): "Comic Rays", Macmillan Encyclopaedia of Physics.
8. Nandedkar, D. P. (2016): "Analysis of cosmic rays from inter-electronic structure of the electron", Vol. 2, No. 3, pp.220-225, Phys. Journal (PSF), (AIS), USA.
9. Feinberg, G. (1967). "Possibility of Faster-Than-Light Particles". Physical Review 159 (5): 1089–1105.
10. Ramo, S., Whinnery, J. R. and Van Duzer, T., (1970): "Fields and Waves in Communication Electronics", Wiley Eastern Private Limited", First Edition, First Wiley Eastern Reprint, New Delhi.
11. French, A. P., (1958): "Principles of Modern Physics", Wiley International Edition, New York, London etc.
12. Richtmyer, F. K., Kennard, E. H., and Lauritsen, T., (1955): "Introduction to Modern Physics", Fifth Edition, International Student Edition, MaGraw Hill Book Co, Inc., New York, Toronto, London etc.
13. Jain, G. C., (1967): "Properties of Electrical Engineering Materials", Harper & Row, Publishers, New York, Evanston and London.
14. Parker, P., (1957): "Electronics", Reprinted Published First Edition, Edward Arnold Publishers Ltd., London.