A Solution to the Dark Matter-Baryon Conspiracy

Man Ho Chan^*

Department of Science and Environmental Studies, the Hong Kong Institute of Education, Hong Kong, China

Abstract

Observations indicate that the total density distribution is almost isothermal in many galaxies. In this article, I show that if the feedbacks from supermassive black hole and photon-baryon interaction are important, the total density distribution would become isothermal naturally. This explains why most rotation curves in galaxies are generally flat for the outer region and provides a solution to the dark matter-baryon conspiracy.

Keywords

Dark Matter, Supermassive Black Hole, Galaxies, Velocity Dispersion

Received: August 9, 2015
Accepted: August 27, 2015
Published online: September 7, 2015

@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/

1. Introduction

In the past few decades, observations indicate that there are some universal properties exist in galaxies. In particular, the most important feature is that the rotation curves of galaxies are nearly flat in the outer region [1,2]. Although dark matter dominates the mass of a galaxy, the contribution of baryonic mass to total mass is not negligible. The baryonic mass can account for 10-20 % of the total mass. Interestingly, the combination of the contributions of dark matter and baryons results in a flat rotation curve. The transition from disk to halo domination is very smooth. It seems that the dark matter and baryons cooperate with each other to achieve a flat rotation curve [3]. This problem is known as the halo-disk conspiracy (for spiral galaxies) [3] or the dark-spheroid conspiracy (for elliptical galaxies) [4]. Here, I call it the dark matter-baryon conspiracy.

Unfortunately, the collisionless dark matter model does not produce the observed flat rotation curves. Numerical simulations indicate the dark matter density profile goes like  near the center and  at large radius (known as the NFW profile), which does not match the observed flat rotation curves [5]. For example, Gentile et al. (2007) and de Naray et al. (2009) point out that the NFW profile is unable to bring the data into agreement with observations. The NFW fits are generally poor for many galaxies [8,9]. Instead, many recent studies indicate that the dark matter density distribution follows isothermal distribution  rather than the NFW profile. Koopmans et al. (2009) analysed 58 early-type galaxies and obtained the total density . Later, Grillo (2012) studied a sample of 39 massive early-type lens galaxies and obtained . Recently, Chae et al. (2014) study 2000 nearly spherical SDSS galaxies and get , which is very closed to the isothermal distribution.

In fact, the NFW profile can get good agreement with observations in clusters of galaxies [13,14]. If the NFW profile is really universal for dark matter in all scales, there may exist some mechanisms such that the dark matter density is altered and becomes isothermal distribution.

Historically, the effects of baryons were seen as merely a passive component during the assembly of galaxies because the total baryonic mass is much less than the total dark matter mass [15]. Nevertheless, recently, many studies start to realize that the effects from baryons can significantly affect the dark matter component. For example, Blumenthal et al. (1986) show that the baryonic infall can explain the contraction of dark matter halo. Also, the dark matter core can be formed due to various baryonic processes, such as supernova feedback [17,18] and dynamical friction [19] (see Pontzen and Governato (2014) for a review on this issue). Therefore, it is possible for the dark matter density changed from the NFW profile to the isothermal profile during the galaxy formation due to baryonic effects [20].

Recently, Remus et al. (2013) simulate the elliptical galaxies formed in isolated binary mergers within the cosmological framework. They find that all galaxies have flat intrinsic combined stellar and dark matter velocity dispersion profiles, which is equivalent to the isothermal distribution. The combined system of stars and dark matter act as a natural attractor in the process [4]. In this article, I show by an analytic framework that the isothermal distribution of total density profile in a galaxy is a consequence of photon baryon interactions. If the photon-baryon interactions and the feedback from supermassive black hole are important, the isothermal distribution would arise naturally.

2. The Total Mass Density Distribution

By using Virial theorem, we notice that the temperature at the early stage of galaxy formation is high ( K) due to gravitational attraction, where  50 kpc and  are the size and mass of a typical galaxy respectively, and  is the average mass of a baryonic gas particle.

It is commonly believed that each galaxy have a supermassive black hole at the center. The power emitted by the accretion disk L around the supermassive black hole is very high and thus heat up the surrounding gas. The flux of the power outflow from the accretion disk is . In equilibrium and for such a high temperature, the cooling rate of the baryons by Bremsstrahlung radiation balances the heating rate by the power outflow. The power absorbed by a thin shell with thickness  is directly proportional to the optical depth , where  is the number density of baryons and σ is the energy absorption cross section. Therefore we have

,                   (1)

where  is the efficiency of energy absorption and erg cm^-3 s^-1 is the coefficient of Bremsstrahlung radiation.

In fact, the photons emitted by the Bremsstrahlung radiation would interact with the baryonic gas particles again so that a temperature gradient is established. The mean free path of a photon is about 10 kpc, which means a photon would interact with gas particles by several times before escaping from a galaxy. The temperature gradient can be obtained by

,                                  (2)

where  J K^-4 m^-3 and  is the Thomson cross section. For erg s^-1,

 K and  cm^-3, we get K kpc^-1, which is extremely small throughout a galaxy. Due to this small temperature gradient, the heat transfer by conduction is also very small. Therefore, the temperature profile can be regarded as a constant.

Since T and L are constants and we assume that  and  do not vary with , we get

,                       (3)

which is an isothermal distribution.

On the other hand, the total density distribution  can be described by the Jeans equation [21]:

,                             (4)

where  is the velocity dispersion of baryons and  is the total gravitational potential, which includes the information of . By Virial theorem, we have  [22]. Therefore,  is also a constant. By using the Poisson equation and Eq. (4), we can get

,               (5)

From Eq. (3), we get . Putting this relation into Eq. (5), we get

,                               (6)

which is also an isothermal distribution. Therefore, if the temperature is high and the mean free path is short enough, the baryonic density and total matter density would become isothermal distribution (). This result is consistent with the observations that most galaxies have isothermal distribution and flat rotation curves. In Fig. 1, we compare our result with the data of a dwarf galaxy DDO 39. By adding a small core (2 kpc) to match the data for small , our result agrees with the observed data, especially for large . We can see that the enclosed mass increases linearly with  for  pc, which agrees with the result in Eq. (6).

Moreover, since the baryon to total mass ratio is given by , we have

,                            (7)

where we have applied Virial theorem . Therefore, our analysis predicts  at the very beginning during the galaxy formation.

Nevertheless, the above analysis is mainly focusing on the energy balance. At the central part of a galaxy, the outflow and the momentum transferred from the accretion disk is important. It is now believed that the baryonic outflow causes the formation of core at the galactic center [15]. Therefore, the isothermal distribution obtained from the above analysis cannot be applied to the central region of a galaxy.

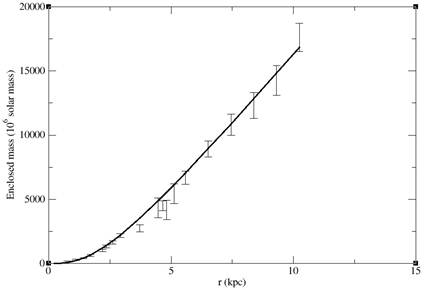
Fig. 1. The enclosed mass of dwarf galaxy DDO 39 (we use the data from ref. [23]). The solid line is the empirical fit using Eq. (6) with a core-size of 2 kpc.

3. Discussion and Conclusion

We show in this article that the density distribution would become isothermal if the photon-baryon interactions and the power from the supermassive black hole are important. This result is consistent with the observations that the total density distribution is isothermal in many galaxies (see Fig. 1 for an example). Previously, Remus et al. (2013) have already shown that the isothermal distribution is a stable attractor under non-equilibrium interactions between baryons and dark matter. Here, we show that even in equilibrium, isothermal distribution is also a stable configuration during galaxy formation. Hence, this result provides a solution to the dark matter-baryon conspiracy in galaxies. Moreover, this result also supports the suggestions that the feedbacks from supermassive black hole and baryons have essential roles in galaxy formation [11,24]. The dark matter distribution can be significantly altered by these feedbacks, just similar to effect on core formation at the center of galaxy.

Note that the total density distribution is globally isothermal only, which means that the rotation curve is generally flat. In fact, local density fluctuations throughout a galaxy are always possible so that most rotation curves are fluctuating about a constant value. On the other hand, we show that both baryonic and dark matter distributions are isothermal. Therefore, the ratio of the baryonic to total mass should be constant throughout a galaxy. This result is confirmed recently by observations that the ratio of the baryonic to total rotation velocity is nearly constant for a long distance from galactic center within a galaxy [25].

To conclude, we provide a simple analytic framework to address the dark matter-baryon conspiracy. This suggests an attractor for isothermal distribution of total matter. The resulting density profiles of both baryons and total matter are also consistent with recent observational data. Moreover, we predict , which can be tested by data from high-redshifted galaxies in the future observations.

References

1. Y. Sofue, ApJ 458 (1996), 120.
2. Y. Sofue, and V. Rubin, Annu. Rev. Astron. Astrophys. 39 (2001), 137.
3. E. Battaner, and E. Florido, E., Fund. Cosmic Phys. 21 (2000), 1.
4. R.-S. Remus, A. Burkert, K. Dolag, P. H. Johansson, T. Naab, L. Oser, J. Thomas, ApJ 766(2013), 71.
5. J. F. Navarro, C. S. Frenk, and S. D. M. White ApJ 490 (1997), 493.
6. G. Gentile, C. Tonini, and P. Salucci, Astron. Astrophys. 467 (2007), 925.
7. R. K. de Naray, S. S. McGaugh, and J. C. Mihos, ApJ 692 (2009), 1321.
8. S. A. Kassin, R. S. de Jong, and B. J. Weiner, ApJ 643 (2006), 804.
9. L. Chemin, W. J. G. de Blok, and G. A. Mamon, AJ 142 (2011), 109.
10. L. V. E. Koopmans, et al., ApJ 703 (2009), L51.
11. C. Grillo, ApJ 747 (2012), L15.
12. K.-H. Chae, M. Bernardi, and A. V. Kravtsov, MNRAS 437 (2014), 3670.
13. E. Pointecouteau, M. Arnaud, and G. W. Pratt, Astron. Astrophys. 435 (2005), 1.
14. A. B. Newman, T. Tommaso, R. S. Ellis, D. J. Sand, C. Nipoti, J. Richard, and E. Jullo, ApJ765 (2013), 24.
15. A. Pontzen, and F. Governato, Naure 506 (2014), 171.
16. G. R. Blumenthal, S. M. Faber, R. Flores, and J. R. Primack, ApJ 301 (1986), 27.
17. A. V. Macció, G. Stinson, C. B. Brook, J. Wadsley, H. M. P. Couchman, S. Shen, B. K.Gibson, and T. Quinn, ApJ 744 (2012), L9.
18. J. Peñarrubia, A. Pontzen, M. G. Walker, and S. E. Koposov, ApJ 759 (2012), L42.
19. A. El-Zant, I. Shlosman, and Y. Hoffman, ApJ 560 (2001), 636.
20. M. Velliscig, M. P. van Daalen, J. Schaye, I. G. McCarthy, M. Cacciato, A. M. C. Le Brun,and C. D. Vecchia, ArXiV:1402.4461.
21. N. W. Evans, J. An, and M. G. Walker, MNRAS 393 (2009), L50.
22. C. L. Sarazin, X-Ray Emission from Clusters of Galaxies (New York: Cambridge Univ. Press,1988).
23. R. A. Swaters, M. A. W. Verheijen, M. A. Bershady, and D. R. Andersen, ApJ 587 (2003), L19.
24. N. J. McConnell, C.-P. Ma, K. Gebhardt, S. A. Wright, J. D. Murphy, T. R. Lauer, J. R.Graham, and D. O. Richstone, Nature 480 (2011), 215.
25. T. P. K. Martinsson, M. A. W. Verheijen, K. B. Westfall, M. A. Bershady, D. R. Andersen,and R. A. Swaters, Astron. Astrophys. 557 (2013), A131.