On the Bell–Kochen-Specker Paradox

Koji Nagata^{1, *}, Tadao Nakamura²

¹Department of Physics, Korea Advanced Institute of Science and Technology, Daejeon, Korea

²Department of Information and Computer Science, Keio University, Hiyoshi, Kohoku-ku, Yokohama, Japan

Abstract

We use the validity of Addition and Multiplication for a hidden variables theory. First, we provide an example that the two operations Addition and Multiplication do not commute with each other as revealed by the analyses that are performed in a finite set of numbers. Our discussion leads to an initial conclusion that Sum rule and Product rule do not commute with each other in a hidden variables theory. If we accept this conclusion, we do not get the Bell-Kochen-Specker paradox. In more detail, quantum mechanics may accept the hidden variables theory. Next, we discuss the validity of operators under an assumption that Sum rule and Product rule commute with each other. In this case, we indeed get the Bell-Kochen-Specker paradox. We got the non-classicality of macroscopic experimental data observed in the Stern-Gerlach experiment and the double-slit experiment. If we detect  and then we detect , the experiments cannot accept the hidden variables theory. We considered whether we can assign the predetermined "hidden" result to numbers 1 and -1 as in results of measurements with the number of measurements finite (e.g., twice) in the experiments. It turned out that we cannot assign the predetermined hidden result to such results of measurements. The next conclusion indicates interestingly that the Stern-Gerlach experiment cannot accept classical mechanics. The double-slit experiment had led to the same situation, and they were indeed quantum mechanical phenomena.

Keywords

Quantum Nonlocality, Algebra, Set Theory, Formalism

Received: July 29, 2015
Accepted: August 22, 2015
Published online: September 10, 2015

@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/

1. Introduction

The quantum theory (cf. [1-5]) gives accurate and at times remarkably accurate numerical predictions. Much experimental data has explained well the quantum predictions for long time.

On the other hand, the incomplete argument of Einstein, Podolsky, and Rosen (EPR) [6] for a hidden variable interpretation of the quantum theory has been an attractive topic of research [2, 3]. There are two main approaches to study the hidden-variable interpretation of the quantum theory.

One is the Bell-EPR theorem [7]. This theorem says that the quantum predictions violate the inequality following the EPR-locality condition. The EPR-locality condition tells that a result of measurement pertaining to one system is independent of any measurement performed simultaneously at a distance on another system. The dependency has been proved by the entanglement. However, the locality is set by in priori.

The other is the no-hidden-variables theorem of Kochen and Specker (KS theorem) [8]. The original KS theorem says the non-existence of a real-valued function which is multiplicative and linear on commuting operators. In general, the quantum theory does not accept the KS type of hidden-variable theory. The proof of the original KS theorem relies on intricate geometric argument. And, the KS theorem becomes very simple form (see also Refs. [9-13]).

Mermin considered the Bell-EPR theorem in a multipartite state. He derived the multipartite Bell inequality [14]. Greenberger, Horne, and Zeilinger discovered [15, 16] the so-called GHZ theorem for four-partite GHZ state. The quantum predictions by n-partite GHZ state violate the Bell-Mermin inequality by an amount that grows exponentially with n. After all, several multipartite Bell inequalities were reported [17-25]. They also revealed that the quantum predictions violate the local hidden-variable theories by an amount that grows exponentially with n.

The KS theorem was begun with research for the validity of itself by using the inequalities (see Refs. [26-29]). To find such inequalities to test the validity of the KS theorem is particularly useful for experimental investigation [30]. The KS theorem is related to the algebraic structure of a set of quantum operators. The KS theorem is independent of a quantum state under study. One of the authors derives an inequality [29] as tests for the validity of the KS theorem. The quantum predictions violate the inequality when the system is in an uncorrelated state. An uncorrelated state is defined in Ref. [31]. The quantum predictions by n-partite uncorrelated state violate the inequality by an amount that grows exponentially with n.

We cannot assign definite value into each quantum datum. This gives the very simple reason why Bell-Kochen-Specker inequalities are violated in real experiments.

Leggett-type nonlocal hidden-variable theory [32] is experimentally investigated [33-35]. The experiments report that the quantum theory does not accept Leggett-type nonlocal hidden-variable theory. These experiments are done in four-dimensional space (two parties) in order to study nonlocality of hidden-variable theories.

Many researches address non-classicality of observables. And non-classicality of quantum state itself is not investigated at all (however see [36, 37]). Non-classicality of macroscopic quantum datum is not investigated very well.

In this paper, we use the validity of Addition and Multiplication for a hidden variables theory. First, we provide an example that the two operations Addition and Multiplication do not commute with each other as revealed by the analyses that are performed in a finite set of numbers. Our discussion leads to an initial conclusion that Sum rule and Product rule do not commute with each other in a hidden variables theory. In this case, we do not get the Bell-Kochen -Specker paradox. Next, we discuss the validity of operators under an assumption that Sum rule and Product rule commute with each other. In this case, we get the Bell-Kochen-Specker paradox. We got the non-classicality of macroscopic experimental data observed in the Stern-Gerlach experiment and the double-slit experiment. If we detect  and then we detect , the experiments cannot accept the hidden variables theory. We considered whether we can assign the predetermined "hidden" result to numbers 1 and -1 as in results of measurements with the number of measurements finite (e.g., twice) in the experiments. It turned out that we cannot assign the predetermined hidden result to such results of measurements. The next conclusion indicates interestingly that the Stern-Gerlach experiment cannot accept classical mechanics. The double-slit experiment had led to the same situation, and they were indeed quantum mechanical phenomena.

2. The Two Operations Addition and Multiplication Do Not Commute with Each Other

We consider a value V which is the sum of the results of trials. Result of trials is 1 or -1. We assume the number of -1 is equal to the number of 1. The number of trials is 2m. We have

V=2m - 2m=0.                     (2.1)

We derive the possible value of the product  of the value V. It is

.                      (2.2)

We assign the truth value "1" for the following proposition

.                       (2.3)

We have

.                  (2.4)

The value (V=0) which is the sum of the results of the trials is given by

.                     (2.5)

We assume that the possible value of the actually measured results  is 1 or -1. We have

.                 (2.6)

The same value is given by

.                     (2.7)

We only change the notation as . The possible value of the actually measured results  is 1 or -1. We have

   (2.8)

and

.  (2.9)

Here . By using these facts we derive a necessary condition for the value given in (2.5). We derive the possible value of the product  of the value V given in (2.5). We have the following under the assumption that the two operations Addition and Multiplication commute with each other.

             (2.10)

                (2.11)

            (2.12)

               (2.13)

       (2.14)

            (2.15)

The step (2.10) to (2.11) is OK. The step (2.11) to (2.12) is valid under the assumption that the two operations Addition and Multiplication commute with each other. We insert parentheses. The step (2.12) to (2.13) is true since we have only changed the notation as . The above inequality (2.13) is saturated since

   (2.16)

and

. (2.17)

We derive a proposition concerning the value given in (2.5) under the assumption that the possible value of the actually measured results is 1 or -1, that is . We derive the following proposition

.                (2.18)

We do not assign the truth value "1" for the two propositions (2.4) and (2.18) simultaneously. We are in a contradiction. Thus we have to give up the assumption that the two operations Addition and Multiplication commute with each other. Our discussion leads to an initial conclusion that Sum rule and Product rule do not commute with each other in a hidden variables theory. If we accept this conclusion, we do not get the Bell-Kochen-Specker paradox. In more detail, quantum mechanics may accept the hidden variables theory. In what follows, we discuss the validity of operators under an assumption that Sum rule and Product rule commute with each other. In this case, we indeed get the Bell-Kochen-Specker paradox and quantum mechanics does not accept the hidden variables theory, in general.

3. Easy Example That We Cannot Assign Definite Value into Each Experimental Datum

We consider a mean value V to an expected value which is the sum of data in some experiments. The actually measured results of trials are 1 or -1. We assume the number of -1 is equal to the number of 1. The number of trials is 2. Then we have

V=-1+1=0.                       (3.1)

First, we assign definite value into each experimental datum. In this case, we consider the Bell-Kochen-Specker realism.

By using , ,  and , we can define experimental data as follows: , ,  and . Let us write V as follows

.                     (3.2)

The possible value of the actually measured results  is 1 or -1. The same value is given by

.                    (3.3)

We change the notation as . The possible value of the actually measured results  is 1 or -1.

In the following, we evaluate the maximum value of the product  and derive a necessary condition under an assumption that we assign definite value into each experimental datum. We have

VV= (=

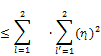
=4     (3.4)

The above inequality (3.4) is saturated since

    (3.5)

and

.   (3.6)

Hear . We derive an assumption concerning the value given in (3.2) under an assumption that the possible value of the actually measured results is 1 or -1, that is . We derive the following assumption concerning the Bell-Kochen-Specker realism

.                 (3.7)

Next, we derive the other maximum value of the product  of the value V under an assumption that we do not assign definite value into each experimental datum. This is quantum mechanical case. From V=0, we have

.                  (3.8)

Thus,

.                   (3.9)

We have the following assumption concerning quantum mechanics

.                  (3.10)

We cannot assign the truth value ``1'' for the two assumptions (3.7) and (3.10). We are in the BKS contradiction. Thus we cannot assign definite value into each experimental datum even though the number of data is two.

4. More General Example That We Cannot Assign Definite Value into Each Experimental Datum

We consider a mean value V to an expected value which is the sum of data in some experiments. The actually measured results of trials are 1 or -1. We assume the number of -1 is equal to the number of 1. The number of trials is 2m. m=1,2,… We have

V=2m-2m=0.                  (4.1)

First, we assign definite value into each experimental datum. Let us write the value (V=0) as follows

.                    (4.2)

We assume that the possible value of the actually measured results  is 1 or -1.

The same value is given by

.                   (4.3)

We change the notation as . The possible value of the actually measured results  is 1 or -1.

By using these facts we derive a necessary condition for the value given in (4.2). We derive the maximum value of the product VV of the value V given in (4.2). We have the following under an assumption that we assign definite value into each experimental datum:

VV=(=

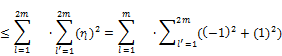
=4             (4.4)

The above inequality (4.4) is saturated since

    (4.5)

and

. (4.6)

Here .We derive an assumption concerning the value given in (4.2) under an assumption that the possible value of the actually measured results is 1 or -1, that is . We derive the maximum value concerning the Bell-Kochen-Specker realism

.                (4.7)

Next, we derive the other maximum value of the product  of the value  under an assumption that we do not assign definite value into each experimental datum. This is quantum mechanical case. From V=0, we have

.                 (4.8)

Thus,

.                 (4.9)

We have the following assumption concerning quantum mechanics

.                (4.10)

We cannot assign the truth value "1" for the two assumptions (4.7) and (4.10). We are in the contradiction. Thus we cannot assign definite value into each experimental datum.

We say the following statement:

We cannot assign definite value into each experimental datum when the number of measurement is even and finite.

Otherwise we are in the BKS contradiction. We are not in the BKS contradiction if we cannot assign definite value into each experimental datum when the number of measurement is even and finite.

5. Conclusions

In conclusions, we have used the validity of Addition and Multiplication for a hidden variables theory. First, we have provided an example that the two operations Addition and Multiplication do not commute with each other as revealed by the analyses that are performed in a finite set of natural numbers. Our discussion has led to an initial conclusion that Sum rule and Product rule do not commute with each other in a hidden variables theory. We do not have got the Bell-Kochen-Specker paradox if we accept the first conclusion. In more detail, quantum mechanics may have accepted the hidden variables theory. It has been not easy to contest the Bohm’s hidden variable theory which is still in a great debate process. We have tried to validate our point on the hidden variable theory using the operators: Additive and Multiplicative. It has been hoped that this article induces further debates on our approach and simplistic determinism.

Next, we have discussed the validity of operators under an assumption that Sum rule and Product rule commute with each other. In this case, we indeed get the Bell-Kochen-Specker paradox. We have got the non-classicality of macroscopic experimental data observed in the Stern-Gerlach experiment and the double-slit experiment. If we detect  and then we detect , the experiments cannot have accepted the hidden variables theory. We have considered whether we can assign the predetermined "hidden" result to numbers 1 and -1 as in results of measurements with the number of measurements finite (e.g., twice) in the experiments. It has turned out that we cannot assign the predetermined hidden result to such results of measurements. The next conclusion indicates interestingly that the Stern-Gerlach experiment cannot accept classical mechanics. The double-slit experiment had led to the same situation, and they were indeed quantum mechanical phenomena.

Acknowledgement

We thank the reviewer of the paper.

References

1. J. J. Sakurai,Modern Quantum Mechanics(Addison-Wesley Publishing Company, 1995), Revised ed.
2. A. Peres,Quantum Theory: Concepts and Methods(Kluwer Academic, Dordrecht, The Netherlands, 1993).
3. M. Redhead,Incompleteness, Nonlocality, and Realism(Clarendon Press, Oxford, 1989), 2nd ed.
4. J. von Neumann,Mathematical Foundations of Quantum Mechanics(Princeton University Press, Princeton, NewJersey, 1955).
5. M. A. Nielsen and I. L. Chuang,Quantum Computation and Quantum Information(Cambridge University Press,2000).
6. A. Einstein, B. Podolsky, and N. Rosen, Phys. Rev.47, 777 (1935).
7. J. S. Bell, Physics1, 195 (1964).
8. S. Kochen and E. P. Specker, J. Math. Mech.17, 59 (1967).
9. C. Pagonis, M. L. G. Redhead, and R. K. Clifton, Phys.Lett. A155, 441 (1991).
10. N. D. Mermin, Phys. Today43(6), 9 (1990).
11. N. D. Mermin, Am. J. Phys.58, 731 (1990).
12. A. Peres, Phys. Lett. A151, 107 (1990).
13. N. D. Mermin, Phys. Rev. Lett.65, 3373 (1990).
14. N. D. Mermin, Phys. Rev. Lett.65, 1838 (1990).
15. D. M. Greenberger, M. A. Horne, and A. Zeilinger, inBell’s Theorem, Quantum Theory and Conceptions of theUniverse, edited by M. Kafatos (Kluwer Academic, Dordrecht, The Netherlands, 1989), pp. 69-72.
16. D. M. Greenberger, M. A. Horne, A. Shimony, and A. Zeilinger, Am. J. Phys.58, 1131 (1990).
17. S. M. Roy and V. Singh, Phys. Rev. Lett.67, 2761 (1991).
18. M. Ardehali, Phys. Rev. A46, 5375 (1992).
19. A. V. Belinskii and D. N. Klyshko, Phys. Usp.36, 653 (1993).
20. R. F. Werner and M. M. Wolf, Phys. Rev. A61, 062102 (2000).
21. M. Zukowski, Phys. Lett. A177, 290 (1993).
22. M. Zukowski and D. Kaszlikowski, Phys. Rev. A56, R1682 (1997).
23. M. Zukowski and C. Brukner, Phys. Rev. Lett.88, 210401 (2002).
24. R. F. Werner and M. M. Wolf, Phys. Rev. A64, 032112 (2001).
25. R. F. Werner and M. M. Wolf, Quantum Inf. Comput.1, 1 (2001).
26. C. Simon, C. Brukner, and A. Zeilinger, Phys. Rev. Lett.86, 4427 (2001).
27. J.-A. Larsson, Europhys. Lett.58, 799 (2002).
28. A. Cabello, Phys. Rev. A65, 052101 (2002).
29. K. Nagata, J. Math. Phys.46, 102101 (2005).
30. Y. -F Huang, C. -F. Li, Y. -S. Zhang, J. -W. Pan, and G. -C. Guo, Phys. Rev. Lett.90, 250401 (2003).
31. R. F. Werner, Phys. Rev. A40, 4277 (1989).
32. A. J. Leggett, Found. Phys.33, 1469 (2003).
33. S. Groblacher, T. Paterek, R. Kaltenbaek, C. Brukner, M. Zukowski, M. Aspelmeyer, and A. Zeilinger, Nature (London)446, 871 (2007).
34. T. Paterek, A. Fedrizzi, S. Groblacher, T. Jennewein, M. Zukowski, M. Aspelmeyer, and A. Zeilinger, Phys. Rev. Lett.99, 210406 (2007).
35. C. Branciard, A. Ling, N. Gisin, C. Kurtsiefer, A. Lamas-Linares, and V. Scarani, Phys. Rev. Lett.99, 210407 (2007).
36. M. F. Pusey, J. Barrett, and T. Rudolph, Nature Phys.8, 475 (2012).
37. K. Nagata and T. Nakamura, International Journal of Emerging Engineering Research and Technology, Volume 3, Issue 6, 78 (2015).