On the Definition of Dark Exciton’s Spins Interactions: Based on Quantum Field Theory

Arezu Jahanshir^*

Department of Eng. Physic, Buein Zahra Technical University, Qazvin, Iran

Abstract

The mechanism of electron-hole interactions of the exciton system in GaAs and GaAlAs, semiconductors could be described by the quantomechanical approaches. The main study based on a two-body Coulomb system comprising electron-hole in an external magnetic field. Todays, modern technology allows semiconductor nanostructures like quantum dots and quantum wires to be synthesized in which a finite number of electrons are confined in a bounded volume of the order of atomic sizes. Controlling over the properties of exciton system is very important in spintronics technology. As electron-hole have spin, so in the external magnetic field we should present new quantum characteristics like different spin 1/2 and 3/2. On the other hand, exciton system separated on bright (electron-light hole system) and dark quasi-systems. A dark exciton is a quasi-system formed from a single electron bound to a single heavy hole with spin projection ± 3/2. Based on spins interactions in electron-hole system, we got too many different states in bounding electron with different type of hole that given us new characteristics in exciton system. The characteristics of this type of fundamental excitation, if confined inside a semiconductor, could be advantageous in modern spintronics technology and future super computers. As we know electron/hole with spin ± 1/2 are scalar charged particles. The description of the bound state characteristics of dark exciton is one of the main interesting subjects in quanto-optical mechanics; therefore calculation of relativistic corrections becomes necessary. We will consider this problem, according to the asymptotic behavior of the loop function in the scalar electrodynamics field and method oscillator representation in quantum physics. The method presented in this paper considers relativistic with Coulomb interaction. This work paves the way for the exploration of the fundamental properties and of the potential relevance of heavy-hole spin in quantum technologies. Therefore, according to the basis investigation of the asymptotically behavior of the loop function of scalar particles in the external electromagnet field and quantum field theory (QFT), the theoretical information on the exciton exotic quasi-system’s Hamiltonian, including the relativistic (spins) and nonperturbative effects were described.

Keywords

Exotic Bound State, Spin Orbital Interactions, Heavy Hole, Green’s Function

Received: July 29, 2015
Accepted: August 21, 2015
Published online: September 10, 2015

@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/

1. Introduction

We describe the creation of spins interactions in the dark exciton by using QFT methods and determine how relativistic and quantum characters of particles could be effect on bounding states and give new characteristic in nanoscales devices [1-3]. Quanto-optical properties and effects of dark exciton are crucial in spintronics technology [3,4]. We investigate the relationship between the spins and relativistic structures effects in total Hamiltonian. The exciton binding energies and quanto-optical interactions in semiconductors will be described based on Coulomb interactions and principles calculations based on the oscillator representation method (ORM), functional path integral theory and using Green’s functions [5-7]. Our results clearly show that relativistic interactions are the important parameters to determine exact and total eigenvalue of Hamiltonian interactions in exciton bound state. These effects are quantized by electronic structures obtained from the quantum theory; thus, our approach can be applied to understand the heavy hole effects in complex semiconducting materials. The result of the relativistic and electrostatic Coulomb interactions between electrons and holes because of the requirement that the wave function of a pair of electron-holes be symmetric or anti-symmetric with respect to the interchange of electron-hole coordinates and spins become spin-dependent. If the electron-hole spins are parallel, we have dark exciton system in the opposite case, when the spins are antiparallel will have bright exciton bound states or exciton-polariton system. Therefore in spintronics theories, parallel and antiparallel spins have different and separated characteristics in space or inside semiconductors. Therefore, the description of the electron and heavy-hole is one of the general problems in spintronics technology and theoretical quantum information subjects. This bound state is studied in QED by many authors. To exact description and find electron-hole bound characteristics, we need introduce with new methods based on QFT, nonrelativistic quantum electrodynamics and relativistic quantum dynamics. In this case, we try to study electron-hole bounding system based on QFT and ORM [5-8] One of the corrections in QFT and QED can be classified as quanto-optical effects that exit from relativistic character of nanoscale systems [11-12] At present the technical achievements in spintronics technology make it possible to create the exotic electron-hole systems with both conduction and valence band edge hole states. However, the interactions is not strong because of small range of the Coulomb coupling constant (α= 1/137), the calculation of relativistic corrections is not necessary. But it is better to study relativistic effects on electron-hole bound states [11,12]. So the subjects of the relativistic nature interaction and total Hamiltonian within the frame work of the phenomenological potential model of fermions based on QFT and QED will be describe and determined in this paper. We will consider these subjects (spins interactions), according to the asymptotic behavior of the loop function in the scalar electrodynamics field and ORM in quantum physics.

2. Origin of Spins Interactions Hamiltonian

Determination the energy spectrum and eigenvalue of the total Hamiltonian of systems that contain of nonrelativistic, spins, nonperturbative and perturbative Hamiltonian usually are described by the Schrödinger equation with a special potential [12-14]. The basic subject in exotic and non-exotic bound states system is to complete solution of this equation for the Coulomb potential. One of the methods is ORM. In ORM a wave function is expanded over the oscillator basis in which coordinate and momentum are expressed through the creation and annihilation operators [5-6]. The ORM in the nonrelativistic/relativistic Schrödinger equation is proposed to calculate the energy spectrum for central symmetric potential allowing the existence of bound state. The method applied to describe and calculate the energy spectrum and spin interactions coefficients of exotic bound systems in Coulomb potential (for details see [7-9]). It is well known that for determining the energy and these coefficients one should determine the eigenvalue of the each Hamiltonian interaction with Coulomb potential in the one equation that named total Hamiltonian of bounding system. For this aim we consider the Schrödinger equation for the wave function of orbital excitation because of include spins interactions. For the Coulomb potential the asymptotic behavior of wave function at large distance, is known [10-12]. Therefore we just modify the variables in the Schrödinger equation by substituting new parameters that describe new space of interactions and give us some conditions that we could find total Hamiltonian based on QFT and ORM. So the nonrelativistic/relativistic Schrödinger equation in oscillator representation method for the Coulomb potential will be obtained. The result of Coulomb energy spectrum in the zero approximation of oscillator representation for electron-hole system was determined and it is in good agreement with the exact values. In relativistic limit, the total Hamilton of particles should be determined through surveying spin-spin and spin-orbital effect between particles in electron-hole system in a quantum dots. Hence, force between electron-hole is the force which is result of holes effects, quadrupole forces and the force resulted from electron and holes relative movements. To have simplicity, we have only considered the potential resulted from first two forces. So final potential in quantum dots will be equal to vector potential resulted from uni-photon transaction and the potential resulted from electrons’ confinement and spin effect. Therefore spins interactions using ORM with moving to spherical coordination system would be determined. Spins interactions and equations formed by two scalar particles are provided in 1991, so we will use them for electron-hole spins interactions in dark exciton. Spins interactions in exciton are a phenomenon that manifest in lifting the degeneracy of electron-hole energy levels in semiconductors. In semiconductor quantum dots, the relativistic Schrödinger equation is frequently used as a first approximation in electron-hole structures. Relativistic Hamiltonian interactions lead to describe spins interactions and nonperturbative correction via relativistic effects of bounding states. Therefore spins interactions and new added part to the total Hamiltonian can be included as a relativistic correction to the Schrödinger equation [9]. For this purpose one has to consider the equation, which is the basic equation in spintronics physics, including the electron-hole spins and its nonperturbative-relativistic behavior in semiconductors.

3. QFT and Interactions

We can determine characteristic and principals of fundamental particles effects by using usual field theories and characteristics. But when particles interact to each other usual theories could not completely describe interactions. Hence, we have to examine more complicated theories that include interaction terms and interaction space like QED, QCD and etc. This theory in micro-world is sum of QFT, QED and QCD (for colored particle). QFT and QED are the mathematical framework for all elementary particle physics. They are the powers theories for describing interactions between charged particles in electromagnetics field. As we know relativity characteristic is inside the total Hamiltonian of fundamental particles interactions. On the other hand, relativistic correlation is in the particle’s wave function. Description of relativistic characteristic in charged interactions like electron-hole, electron-positron and etc., will be based on QFT and QED that exist in the total Hamiltonian interaction. Relativistic Hamiltonian is more appealing for describes all interactions of spins. Spin–spin and spin-orbital coupling is a main relativistic effect and essential for the calculation total Hamiltonian. In dark exciton system containing electron and heavy-hole the effects on total Hamiltonian affected by spins coupling tend to have the 1/2 and 3/2 order of magnitude as those caused by electron-hole correlation. Therefore, the starting points for all theoretical calculations are the relativistic quantum mechanical equation of motion, for electrons and holes. In the paragraph we have briefly presented an alternative approaches to obtain the exact total Hamiltonian interactions in dark exciton system and described relativistic Hamiltonian and relativistic effects of two particles. In a rather informal sense QFT and QED are the extension of quantum mechanics and electromagnetics, dealing with charged particles, over to fields. These will take the form of higher order terms in the Lagrangian and Hamiltonian interactions. So many parameters like perturbation and relativistic effects, we can add to the interaction principals via QFT/QED and its methods. QFT is a theory that is useful for understanding exact aspects of bound states system in particle physics. In this paper we will determine relativistic Hamiltonian and spin coefficients based on QFT and ORM [5-9], which have the start point method on using functional path integrals and creation/annihilation operators.

4. Nonperturbative and Spins Hamiltonian

In general exciton is relatively a stable structure and has a relatively long lifetime (ps to ns), and is important from physical & technological points of view especially in spintronics technology. Nowadays, many academics think that exciton family (dark exciton, bright exciton, diexciton, positive trion and negative trion) become engineers’ toy in a few years. In this section we define and describe Hamiltonian of electron-hole interactions and determine spins or nonperturbative effects in dark exotic exciton system in a semiconductor. As we know, absorption of energy by electrons in semiconductor can describe as immigration of activating electron from capacity band to conductive ban. Electron moves to conductive band and establish a connection with its position in capacity band under Coulomb potential gravity (hole: hole with positive charge). Electron and the heavy-hole with ±3/2 projection of spin start to spin around each other and create a dark exciton system. Interaction, bound state effects, spin effects and particles’ complementary effects are explained through electrostatic forces, electron relative potential and relativistic correlations which result to formation of related electromagnetic field between electron and hole. Schrödinger equation for exciton system is [15-19]:

                                   (1)

Now, based on QFT, QED and QRM, we will present the alternative method to describe the spin properties of the exotic exciton bound state systems by using the investigation of the asymptotic behavior of the polarization loop function for electron-hole in an electromagnetic field. The relativistic and spins interactions are determined via eigenvalues of nonrelativistic and relativistic Hamiltonian in which the kinetic energy term is defined by the constituent mass of bound state, and the potential energy term is determined by Feynman diagrams. The eigenvalues of nonrelativistic/relativistic Hamiltonian derived from the Schrödinger equation are used for determination of the mass and constituent mass of the bound state systems and QFT teqnics which are based on the asymptotical behavior of scalar-charged particles in external gauge field. So, loop function of particles with different masses is considered by averaging on external statistical field and using the Green’ function relation in QFT. The polarization operator in an external electromagnetic field for electron-hole looks like [17,18]:

                 (2)

The Green function  for electron-hole system is determined from equations:

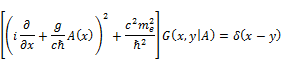
   (3)

For determination of the spins Hamiltonian interactions of the electron-hole exotic system based on QFT, we should define this part of interaction through the exciton mass. In QFT the mass of the bound state is usually defined through the loop function. Correlation between mass and loop function is

                   (4)

and loop function for electron-hole system in the determine as following way

                           (5)

Where

                 (6)

is the interactions potential between electron-electron, electron-hole and hole-hole.

Based on functional and Feynman path integral we simplify the electron-hole loop function and got the bound state mass of exciton system in ORM:

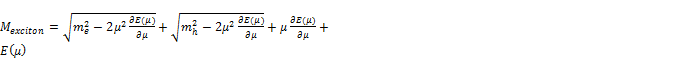                                        (7)

The constituent mass (parameter) is determined by the equation:

             (8)

is the eigenvalue of the total Hamiltonian which is defined by

                                  (9)

By theoretically method that described in the previous rows, we should find the eigenvalue for total Hamiltonian interactions which contain spins interactions. We will use this definition to determine relativistic and spins interactions that is very important subjects in spintronics technology and fundamental theories. As we know spins equations formed by electron and hole, could be determined by separated parts of relativistic, spin-orbital and spin-spin Hamiltonian interactions [19, 5-9]. Election of distance between electron-hole () and effective radius  in dark exciton system () for calculating spin-spin and spin-orbital effects will be so that total vector potential effect resulted from uni-photon exchange  have overlap with the potential resulted from electron converge. Therefore spins Hamiltonian interactions could be calculated by these equations [18,19]:

            (10)

and

                         (11)

where  are mass of electron/hold,  are effective mass of electron /hole , is oscillator frequency of electron, is spin-orbit and is spin-spin Hamilton constant coefficient,. Hamiltonian of relativistic effect will be as follow:

         (12)

where .

5. Conclusion

Semiconductor quantum dots can act as convenient hosts of electron spins, hole spins or excitons. Exciton in the semiconductor quantum dots are considered as main building blocks for quantum and spintronics technologies. A single hole confined in the ground state in semiconductor quantum dot usually has dominant heavy hole character due to quantum confinement. All theoretical studies presented so far have been dealing with dark exciton system. This is because quantum confinement lifts the valence band degeneracy and leads to states with heavy hole character which are energetically well above the bright exciton states. In this article we determined dark exciton total interaction Hamiltonian which contains nonrelativistic and relativistic effects based on the investigation of the asymptotic behavior of the polarization loop function for electron-hole particles in exciton system. Using QFT, QED and ORM we defined the relativistic and nonperturbative Hamiltonian interactions which depend on the speed. Exciton system consists from electron and hole, which move rather from each other by constant by a velocity. From (12), we can see that the nonperturbative component gives orbital-excited state. Thus nonperturbative component is connected to a relativistic nature of a system. Therefore, based on total Hamiltonian new descriptions of spins and nonperturbative effects in nanostructure could be rapidly increase which directly effected on spintronics technology.

References

1. D. L. Owen, In-place bonding ofGaAs/InGaAs/GaAs heterostructures to GaAs, Semicond, Sci. Technol. 24, 035011, 2009.
2. J. D. Plumhof, et al. Experimental investigation and modeling of the fine structure splitting of neutral excitons in strain-free GaAs/AlxGa1-xAs quantum dots. Phys. Rev. B 81, 121309, 2010.
3. G. Bester, Electronic excitations in nanostructures: an empirical pseudopotential based approach, J. Phys.: Cond. Matter 21, 023202, 2009.
4. M. Bayer, et al., Fine structure of neutral and charged excitons in self-assembledIn(Ga)As/(Al)GaAs quantum dots, Phys. Rev. B 65, 195315, 2002.
5. M. Dineykhan,G.V. Efimov, "The Schrodinger equation for the BoundStateSystems in the Oscillator Representation", Reports on Mathematical Physics, 36, 287-307, 1995.
6. M Dineykhan, R.G. Nazmitdinov, "On analytical solutions to the problem of the Coulomb and confining potentials", Yad. Fiz. 62, 143-148, 1999.
7. A. Jahanshir, "Mesonic hydrogen mass spectrum in the oscillator representation", Journal of Theoretical and Applied Physics, 3(4), 14-17, 2010.
8. M. Dineykhan, A. Jahanshir, et al., "Effective Hamiltonian in scaler electrodynamics", Preprint, 197(p2-2002 -197), Dubna, Russian, 1-20, 2002.
9. M. Dineykhan, A. Jahanshhir, et al., "Mass spectrum bound state system with relativistic corrections", Journal of physics B: Atomic, Molecular and Optical Physics, 42(1), 145001, 2009.
10. A. Jahanshir, "Exotic pi-atom", First ICP, Iran, 679-682, 2004.
11. A. Jahanshir, "Hamiltonian Multiplex Interaction Based on Excitons Effect in Semiconductor QCs", Scientific Journal of Pure and Applied Sciences, 3(11), 878-880, 2014.
12. A. Jahanshir, "Spin-Orbital Effect of Diexciton in Quantum Dots", American Journal of Condensed Matter Physics, 2(3), 57-62, 2012.
13. P.Y. Yu, M. Cardona, "Fundamental of Semiconductors", 3^rd edn., Springer, Berlin, 2001.
14. J.M. Luttinger, "Quantum Theory of Cyclotron Resonance in Semiconductors: General Theory" Phys. Rev. 102, 1030, 1956.
15. W.Greiner and Y.Reinhort, Quantum Electrodynamic", 1^st edition, Springer- Verleg, 1992.
16. M. Dineykhan, G.V. Efimov and Kh. Narmsrai, "Investigation of Green’s Functions and the Parisi-Wu Quantization Method in Background Stochas­tic Fields", Fortsh. Phys., 39, 259-318, 1999.Springer- Verlag, Berlin, 1995.
17. R.P. Feynman, A. P. Hibbs, "Quantum Mechanics and Path Integrals", New York McGraw-Hill, 1965.
18. W. Lucha, F. Schoberl, D. Gromes," Bound states of quarks", Phys. Rep. 200, 127-135, 1991.
19. M.I. Dyakonov, V.I. Perel, Z. Eksp., "Theory of optical spin orientation of electrons", Teor. Fiz. 60, 1954, 1971; Sov. Phys. JETP 33, 1053, 1971.