Temperature Dependent Spectral Systematic Error in Optical Measuring Systems

A. V. Polyakov^*

Department of Radio Physics and Computer Technology, Belarussian State University, Minsk, Belarus

Abstract

The method of theoretical estimation of the optoelectronic measurement systems systematic error, arising due to temperature changes is proposed. Mathematical models of the temperature dependence of the Ge -and InGaAs-photodiodes spectral responsivity, correction factor and noise equivalent power for optical time domain reflectometer was developed. It showed significantly better correlation of the results with experimental data in comparison with the triangular and Gaussian approximation. The developed model permits further improvement of accuracy in fiber-optic measurements based on Ge- and InGaAs- photodiodes, especially in the near-infrared wavelength region.

Keywords

Optical Measurement, Semiconductor Photodetector, Spectral Responsivity, Temperature Error

Received: July 9, 2015
Accepted: August 28, 2015
Published online: September 14, 2015

@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/

1. Introduction

Optical measurements play an important role in a variety of scientists, medical, and industrial application. For last decades the direction using optical radiation and unique properties of optical environments for registration of various physical influences was generated. The successes in the field of semiconductor radiation sources, photoreceivers and optical fiber with small attenuation have resulted in occurrence and rough development optoelectronic measuring systems (OMS) on the basis of fiber-optic sensor (FOS). Now process of creation OMS begins with development of mathematical model of FOS functioning with the subsequent computer modeling of FOS work. It allows to estimate, how selected constructive decision corresponds to the given specifications. At this stage it is very important to use adequate and exact mathematical models.

The transformation function of FOS represents complex multistage dependence of registered value on an output of FOS X from external influence :

,      (1)

where  is optical radiation power created by a radiation source at course on it a current ;  is photodiod converter function;  is integrated spectral responsivity of the photoreceiver; kl is losses index of optical radiation power at .

As the fiber-optic channel is enough thermostable, the basic contribution to a temperature error will bring transmitter-receiver block. In this case for an estimation of a temperature error of FOS the finding of the analytical expressions describing temperature dependence of parameters of semiconductor injection lasers (IL) and semiconductor photodetectors is necessary.

An analytical theory based on a model of the internal quantum efficiency of the silicon photodiode and the temperature dependence of the absorption coefficient of silicon is developed [1] and experimental research are carried out [2, 3] to predict the temperature dependence of the spectral responsivity in the wavelength range from 400 to 1020 nm near room temperature. For fiber-optic measurements it is now more commonly used range 1500-1600 nm, corresponding to the maximum spectral responsivity G - and InGaAs-photodiodes. For a theoretical description of the spectral responsivity used triangular [4] or Gaussian function [5]. However, the real spectral characteristics of semiconductor photodiodes intended for fiber optics have a more complex form [6,7]. In addition, we must remember that the change in temperature can significantly affect the output signals of the photodiode especially in the area of 1,55 mm.

2. Calculation of Spectral Characteristics of Semiconductor Photodetectors

According to (1) one of basic FOS regular errors is dependence of semiconductor photodiode (PD) spectral responsivity S(l,q) on wavelength radiation l and temperature q. This error is most essential at the l = 1,55 mm, appropriate to the optical fiber (OF) minimal losses and a maximum of spectral sensitivity for Ge - and InGaAs-PD. For definition  in most cases use empirical curves at any fixed parameters received with the help of expensive certification equipment or a reference material. The basic lack of such approach is its complexity caused besides attraction of certain means, calculation n-order approximation polynomial (depending on desirable accuracy), and also impossibility to look after with its help continuous dynamics of function change depending on temperature. In the given work the approach based on reception of analytical expressions for functions  is offered proceeding from physical laws underlying functioning of the semiconductor photodiode. As a sample the pin-photodiode of a series J16 and С30617, produced by "EG&G Optoelectronics" was chosen. These detectors are high-quality germanium and InGaAs photodiodes designed for the 0,8 to 1,8 mm wavelength ranges. The PD responsivity is determined by a ratio [8]:

,     (2)

where e is electron charge; h is Planck constant; с is light speed, T_tr is transmission coefficient of radiation, a is absorption coefficient, L_pd is thickness of the depleted layer of FD material, x is depth location from a surface of the depleted layer.

As for Ge under action of falling near IR range radiation most probable are the indirect transitions with emitting of Raman phonon, the expression for interzoned absorption coefficient looks like [9]:

  (3)

where N^* = N_AN_D / (N_A + N_D) is reduced impurity concentration, N_A is acceptor concentration, N_D is donor concentration; l_c = 1,24 / [DE(q) + E_R] is long-wave infrared border of radiation absorption, DE is band gap width, DE = 0,66 eV at q = 300 K; E_R –energy of Raman phonon, E_R = 0,037 eV;  is boundary value of photoionization cross-sectional  sm² [10].

Value T_tr is connected with Fresnel reflection of light from border of section of air with refraction index n_a=1 and semiconductor PD with refraction index n_f=3,6. The PD reflection coefficient can achieve 30 %. To reduce this effect, PD surface usually covered by antireflection transparent quartz dioxide film for Ge-FD or silicon nitride (Si₃N₄) film for InGaAs-PD with a thickness in a quarter of wavelength and refraction index n₀=1,46. The transmission coefficient in this case can increase up to 0,82‑0,91, and the maximal sensitivity of a photodetector will be equal S=0,85…0,9 A/W. The transmission coefficient in this case can be calculated according to the following formula:

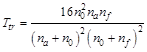.            (4)

Functions  for Ge-PD (solid curve) and InGaAs-PD (dotted line) calculated with the help of the expressions (2) – (4) are submitted in Figure 1. At accounts the following meanings were used for Ge-PD:  sm,  sm, sm^-3, sm^-3, q = 293 K, T_tr = 0,6…0,65 and for InGaAs-PD:  sm,  sm, T_tr = 0,8. The border of PD responsivity in the range of the large wavelength is determined in basic of the width of material forbidden zone, and the fall of responsivity in the range of short waves is connected to absorption of light near to a surface and increase of losses at the expense of superficial recombination of the photoexited carriers. Experimental magnitudes received at research germanium pin-photodiodes of a series J16 (daggers) and InGaAs pin-photodiodes of a series С30617 (triangles) are shown in Figure 1. As it is visible from a Figure 1, experimental and calculated values differ no more than on 5 % in all spectral range. Than the received analytical approximation is much accurately then known Gaussian or triangular approximation.

1 – Ge-PD, 2 – InGaAs-PD

Figure 1. Spectral responsivity of pin-photodiodes.

The offered mathematical model for account is fair not only for Ge-PD, but also for others indirect zone semiconductor photoreceivers consideration of the appropriate parameters describing a material of the semiconductor. It is due to note, that for other types of semiconductor PD it is necessary to take into account, that near to edges of fundamental absorption , where g = 1/2 for the solved direct transitions, g = 3/2 for the forbidden direct transitions g = 2 for indirect transitions.

3. Temperature Dependence of Spectral Responsivity

Depth of the depleted layer L_pd in PD with sharp asymmetrical p-n-junction does not depend on radiation wavelength and is determined by a doping level of the semiconductor, its relative dielectric permittivity e, concentration of intrinsic carriers n_i, return displacement voltage U and temperature:

,(5)

where k is Boltzmann constant, e₀ is electric constant.

For calculations following values, characteristic for Ge-PD were used: U=21 V, e=16.

Dependence of concentration of intrinsic carriers n_i from temperature looks like:

,           (6)

where  and  are effective mass of electron and hole. For germanium of state calculations , , m₀ is free electron mass, kg. Therefore, B= and at q=300 К n_i=.

The temperature dependence of the band gap width is approximated by the expression [11]

.         (7)

where DE(0) is the band gap at 0 K, α_z and β_z are fitting parameters characteristic of a given material. For Ge E(0)=0,74 eV, α_z=4,774×10⁻⁴ eV/K, and β_z=235 K [9].

Between refraction index of the semiconductor n_f and width of forbidden zone DE there is the empirical ratio known as a Moss rule . As DE depends on temperature, hence n_f and T_tr will depend also on temperature. However the lead calculations have shown, that value T_tr decreases approximately for 0,1% at increase in temperature at 10 degrees and such change T_tr it is possible to take no account.

Substituting expressions (3), (5) in the formula (2), we receive expression for S(l,q):

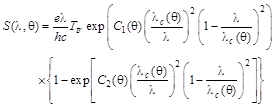, (8)

where ;

Calculate (full and a dash-dot curves) and experimental (circles and crosses) data of spectral responsivity for germanium photodiode at various temperatures are resulted in Figure 2. The temperature factor of spectral responsivity displacement at a point of wavelength 1,5 mm composes 1 nm/K, about the same displacement it is possible to observe in InGaAs-PD in area of 1,65 mm. The analysis of the results given in Figure 2 has shown, that the greatest change of photosensivity with change of temperature will be observed in the measuring systems working on =1,55 mm, and it will be most appreciable given effect to be shown at cooling PD or increase of the radiation wavelength.

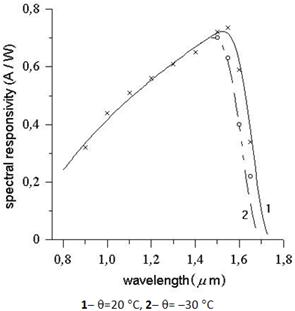
Figure 2. Dependence of germanium PD spectral responsivity from wavelength at various temperatures.

Temperature changes have little effect on the detector responsivity at wavelengths below the peak, but can be important at the longer wavelengths (Figure 3). For example, at 1,2 µm the change in response of a room temperature detector is less than 0,1% per °C, while at 1,7 µm the change is approximately 1,5% per °C (Figure 3). Uniformity of response within the active region of a room-temperature detector is typically better than ± 0,5% at 1,55 mm.

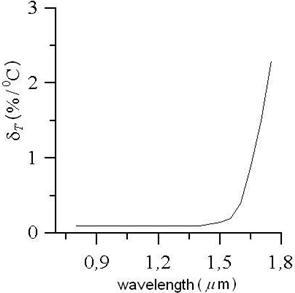
Figure 3. Temperature coefficient of responsivity at 25ºC.

4. Error at Measurement of Optical Radiation Power

Reliability of information transfer on lengthy fiber-optical lines (FOL) is connected with a total level of losses of optical power. The magnitude of these losses is caused both characteristics of fiber optical paths, and losses, introduced due to welding or mechanical connection of optical fiber, the microbends formed during lining FOL, etc. It determines that demanded level of optical power radiated by the semiconductor injection laser which provides necessary probability of an error at reception of information sequence. For definition of losses in field conditions registering optical returnable losses (ORL) are usually used mobile optical time domain reflectometer (ОTDR) type СМА-8800. ORL determined as the relation of power P_e entered in OF to power P_r reflected from OF opposite end and are connected with losses in FOL k_l as follows:

.          (9)

ORL concern to all FOL components, summarizing effects of all sources of losses in system of transfer, being that one of basic FOL characteristics.

The problem of definition ORL by means of OTDR is reduced to exact definition of power of the reflected pulse under condition of stabilization IR radiation power. One of the basic regular errors of power measurement is dependence of responsivity of the photodiode on wavelength of a detected radiation. In that case when spectral distribution of IL radiation power and the specified dependence of PD spectral responsivity are known, the given error can be lowered considerably introduction of corresponding correction.

Considering, that true P_t=P_r and received as a result of measurements valid P_v values of power accordingly are equal:

,    (10)

where P₀ is level of power on the central radiation wavelength l₀, f(l) is the function describing spectral distribution of radiation power and equal f(l₀)=1 for the central wavelength, S(l) is spectral responsivity of the photodiode; expression for correction factor K can be written down as

.        (11)

The analysis of the given expression shows, that the error will be absent in case of a symmetric spectrum of radiation of the laser and linear dependence of the photodiode responsivity on wavelength. However in practice the given conditions are seldom carried out. The formula (11) is fair for LED and multimode injection lasers described a wide radiation spectrum. For singlemode IL, having a narrow radiation spectrum, the formula (11) will become:

.              (12)

Usually for updating results of measurements in methods of data processing OTDR during calibration value K corresponding S(l₀) at a room temperature (25°С) is loaded. However, as testing FOL is carried out in field conditions at an ambient temperature in a range ‑30°С…+40°С, at change of temperature IL generation wavelength l₀ and PD spectral responsivity S(l) will change both wavelength of generation. Therefore in OTDR, intended for work in field conditions, it is necessary to use the correction factor considering not only spectral, but also temperature dependence of FD spectral responsivity.

Substituting the formula (8) in (12), we receive:

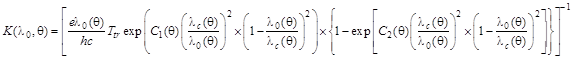  (13)

At definition of correction factor according to (13) at value definition of a temperature error it is necessary to take into account that fact, that change of temperature influences not only spectral responsivity FD, but also wavelength of IL generation. Temperature dependence of radiation wavelength is expressed as follows:

,          (14)

For InGaAsP/InP –IL d_l = 0,09 nm/К for l₀ = 1,55 mm and d_l = 0,11 nm/К for l₀ = 1,3 mm at q=q₀.

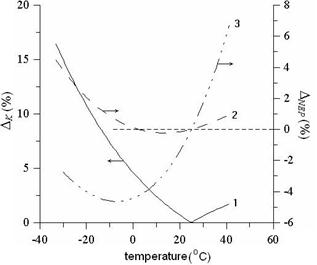
Figure 4. Temperature error of correction factor (1). Temperature relative NEP change of PD (2). Temperature relative NEP change of APD (3).

From Figure 2 follows, that for l₀=1,3 mm change of temperature practically does not influence magnitude S(l) and in this case correction factor K(l₀,q)=K(l₀,q₀)=const in all researched temperature range. However, the majority of measurements by means of OTDR is carried out on l₀=1,55 mm. It is connected by that on the given wavelength is observed not only maximal FD responsivity, but also the minimal optical losses quartz optical fiber. Use IL with l₀=1,55 mm allows to test FOL in the length up to several hundreds kilometers. In this case change of temperature according to Figure 2 will to render essential influence on accuracy of OTDR indications. Сurve 1 in Figure 4 illustrates the value of a regular error arising owing to change of temperature and calculated in view of (13) under formula:

.     (15)

From the schedule follows, that without taking into account influence of temperature the error of correction factor can achieve 15 % that entails an error both at measurement of radiation power, and at definition of losses in FOL. At the same time, according to modern requirements to OTDR, the total regular error in such systems should not exceed 2‑5 %.

One of restrictions of achievement of authentic results of optical power measurement in a wide dynamic range is nonlinearity of PD transformation function. Usually it is considered, that photodiodes are characterized by high linearity in a range of six and more decades of optical power, however exist a number of factors which can break the given law. One of them is noise at registration of low power levels. Nose characteristics of PD are usually expressed in the form of noise equivalent power (NEP):

 (16)

where I_d is dark current, Df is equivalent band of noise frequencies, R_l is load resistance.

For the avalanche photodiodes (APD) working at constant factor of avalanche multiplication M=const, NEP will look like:

,         (17)

,,

where k_i is ratio of electron and holes ionization coefficient (k_i=0,8 for Ge), I_d(q₀) is dark current at room temperature q₀, a is constant factor equal 1‑2 (a=1 for  and a=2 for ).

To similarly expression (15) on the basis of formulas (16) and (17) for PD and APD we shall calculate changes NEP rather NEP (l₀,q₀) under influence of temperature according to expression:

.     (18)

From comparison of plots 2 and 3 in Figure 4 follows, that for PD to make updating OTDR indications in view of increase NEP follows for temperatures q<+3°С and q>+25°С. At the same time at use APD updating should be carried out, only when q>+25°С.

5. Conclusion

The analytical expressions allowing calculating temperature dependence spectral responsivity of Ge- and InGaAs-semiconductor receivers of optical radiation are developed. The received model is much accurately then known Gaussian or triangular approximation and experimental and calculated values differ no more than on 5 % in all spectral range.

Thus, as a result of the lead researches the method of theoretical estimation of the optoelectronic measurement systems systematic error have been received not only to consider spectral properties of semiconductor photodetectors, but also to minimize influence of temperature change on accuracy of FOS measurements. The developed analytical model allows estimating for a design stage a temperature error of any optoelectronic information-measuring systems as which except for fiber-optic sensors can be optical pulse reflectometer, optical measuring equipment of radiation power, measuring equipment of losses in a fiber optical path, etc. The account of the presented correcting dependences in algorithms of data processing in OTDR will allow improving metrological characteristics of such equipment at testing lengthy FOL in field conditions.

References

1. Hartmann, J., Fischer, J., Johannsen, U. and Werner, L. (2001) "Analytical model for the temperature dependence of the spectral responsivity of silicon", J. Opt. Soc. Am. B, Vol. 18, pp. 942–947.
2. Lovinskii, L. S. and Sorokin, V. I. (1992) "Dependence of photodiode spectral sensitivity on temperature", Measurement Techniques, Vol. 35, pp 1288–1290.
3. Sawsan Ahmed Elhouri Ahmed, and Mubarak Dirar Abd-Alla (2013) "Responsivity of silicon photodiodes light & dark current under influence of different magnetic flux intensity and temperature", Elixir Condensed Matter Phys., Vol. 65, pp. 19771–19778.
4. Huck F. O. and Davis, R. E. (1981) "Computational modeling for multispectral sensor design", Proc.SPIE, Vol. 278, pp. 23–31.
5. Sotnikova, G.Yu., Gavrilov, G.A. and Aleksandrov, S.A. (2009) "Performance analysis of diode optopair gas sensors", Proc. SPIE, Vol. 7356, pp. 73561T-1–73561T-11.
6. Shaw, P-S., Larason, T. C., Gupta, R., Brown, S. W. and Lykke,K. R. (2000) "Improved near-infrared spectral responsivity scale", Journal of Research of the National Institute of Standards and Technology, Vol. 105, pp. 689–700.
7. López, M., Hofer, H., Stock, K. D., Bermúdez, J. C., Schirmacher, A., Schneck, F. and Kück Spectral, S. (2007) "Reflectance and responsivity of Ge- and InGaAs-photodiodes in the near-infrared: measurement and model", Applied Optics, Vol. 46, pp. 7337–7344.
8. Gowar, J. (1993) "Optical Communication Systems", Prentice Hall, 696 p.
9. Polyakov, A. V. and Ksenofontov, M. A. (2007) "Temperature error of fibre-optical measuring systems", J. of Engineering Physics and Thermophysics, Vol. 80, pp. 781–785.
10. Polyakov, A.V. and Ksenofontov, M.A. (2010) "Influence of semiconductor photoreceiver spectral responsivity at different temperature on optical measurements", Proc. 5-th International Conference on Advanced Optoelectronics and Lasers (CAOL’2010), Sevastopol, Ukraine, 10–14 September 2010, pp. 199–201.
11. O’Donnell, K. P. and Chen X. (1991) "Temperature dependence of semiconductor band gaps", Appl. Phys. Lett., Vol. 58, pp. 2924–2926.