Liquid Drop Model Prediction for Fusion Interaction Cross Section, Binding Energies and Fission Barriers on the Nucleus–Nucleus Interactions

A. Abel-Hafiez^*

Experimental Nuclear Physics Dept., Nuclear Research Centre, AEA, Cairo, Egypt

Abstract

The liquid drop model(LDM) is used to calculate and describe the binding energies (BE) as a function of the mass number (A) for the most stable nuclei, liquid-drop fission barriers for some heavy nuclei, b-coefficients for the isobaric mass multiplet equation (IMME), Probability profile of ²⁰⁸pb, fusion cross section of some nuclear reactions and calculations for root mean square (rms) charge radii as a function of the atomic number. Some of our calculated characteristics are compared with experimental data, it`s found that there is a good agreement between our calculations and that data. Also, our LDM calculations gave a good agreement with the quantum molecular dynamic (QMD) calculations.

Keywords

Modeling, Liquid Drop Model, Nucleus-Nucleus Interactions

Received:June 10, 2015
Accepted: June 17, 2015
Published online: July 15, 2015

@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/

1. Introduction

The liquid drop model (LDM) of the nucleus was historically the first model to be proposed as an explanation of the different properties of the nucleus. Since it has regained interest in recent times. The idea of considering the nucleus as a liquid drop originally came from considerations about its saturation properties and from the fact that the nucleus has a very low compressibility and a well defined surface. For instance, the mean distance of two particles in a liquid is roughly given by the value at which the interparticle force has its minimum value, which for nuclei would be ~0.7 fm. However, nucleons in nuclei are, on the average, ~2.4 fm apart. One reason for this big difference as compared with an ordinary Liquid is that the nucleons obey Fermi statistics and a nucleus is thus a quantum fluid. The Pauli principle prevents the nucleons from corning too close to one another. Thus scattering events are very scarce in a quantum fluid, whereas in an ordinary fluid they are predominant.

It is more than 60 years now since the first successful application of the charged liquid-drop model to describe the nuclear binding energies. Brilliant extensions of the Bethe-Weizsacker nuclear drop concept by Meitner and Frisch and by Bohr and Wheeler have been obtained in 1939 and used to explain the nuclear fission phenomenon. Since then many papers have been devoted to the nuclear liquid-drop model formalism and its improvements. Various new terms in the corresponding energy expressions have been proposed but the basic concept of the charged liquid drop which could deform and fission remained valid. It is worth reminding at this point that already in 1953 Hill and Wheeler concluded on the basis of the Fermi gas model, that a curvature dependent term proportional to A^1/3should exist in the liquid-drop energy functional. The curvature term was later studied, where its magnitude was adjusted to the experimental fission-barrier heights known at that time [1-4].

Temporary Address: Faculty of Education, Hadramout University, Yemen Republic

Nuclei are bound due to the overall attractive strong interactions between nucleons. The strong interaction arises from the exchange of mesons. The interactions are short ranged and occur mainly between neighboring nucleons. In addition, the nuclear interaction saturates, resulting in a nearly constant interior nucleon density and a surface radius approximately equal to 1.2 A^1/3. The analogy of this situation with a droplet of liquid, results in the liquid drop model for the nuclear binding energies in which the binding energy is expressed in the form[5-7]:

The four terms on the right-hand side are referred to as the volume, surface, Coulomb. and symmetry energy terms, respectively. The first term represents the nearest neighbor attractive interaction between nucleons, and the second term represents the correction due to the fact that the nucleons on the surface only interact with those in the interior. The third term is due to the Coulomb repulsion between protons. The fourth term called the symmetry energy arises because the proton-neutron strong interaction is on the average more attractive than the proton-proton or neutron-neutron strong interactions and because the total kinetic energy is minimized when N = Z. The constant a3=0.697 MeV is fixed by the Coulomb interaction and the nuclear size. Typical values of the liquid-drop constants that reproduce the average trends in the experimental data are given by a1 = 15.49 MeV, a2 = 17.23 MeV and a4 = 22.6 MeV

The fission shapes were investigated long time ago by minimizing the sum of the Coulomb and surface energies using mainly a development of the radius in Legendre polynomials. This leads to fission valley through very elongated shapes with shallow necks and difficulties to precise the position of the scission point where the rupture of the bridge of matter between the nascent fragments occurs. Figure 1 shows the schematic diagram for the LDM of fission and binding energy of a nuclei.

The interest in heavy ion fusion reactions at sub-barrier energies has grown considerably in recent years. This interest has arisen from the possibility that such reactions could lead to the formation of super heavy elements, and also from the information they could provide about the interaction of heavy ions in close proximity.

The aim of the present work is using the classical version of the liquid drop model in prediction and calculation of some characteristics for nuclei and nuclear reactions. That version of the liquid-drop model adjusted to the up-to-date experimental masses and fission barriers.

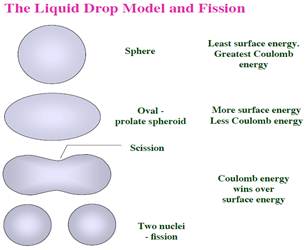
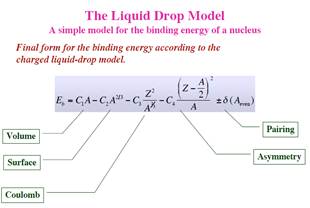
Fig. 1. Scheme for the LDM of fission (upper) and binding energy of a nuclei (lower).

2. Theory

The macroscopic total energy is the sum of the Rotational Liquid-Drop Model energy and the nuclear proximity energy [8]. Constant density and volume conservation are assumed [9-11].

Where the volume E_V, surface E_S and Coulomb E_C energies are given by:

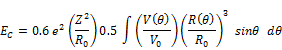
where A, Z and I = (N - Z )/A are the mass, charge and relative neutron excess of the compound nucleus. V (θ) is the electrostatic potential at the surface of the shape and V₀ the surface potential of the sphere. The volume and surface coefficients a_v, a_s and the effective sharp radius R₀ are defined as:

The surface and volume asymmetry coefficients take on the values:

When the two fragments (or colliding nuclei) are separated:

where A_i, Z_i, R_i and I_i are the masses, charges, radii and relative neutron excesses of the fragments and r the distance between the mass centers. The discontinuity of a few MeV which appears at the contact point when Z₁/A₁ and Z₂/A₂ are very different has been removed linearly from the contact point to the sphere since it is due to the progressive rearrangement of the nuclear matter.

The rotational energy has been determined within the rigid body ansatz. Indeed, it has been shown that corrective terms arising from the orbital motion and the spin degrees of freedom roughly cancel each other, particularly at large deformations.

The shell corrections have been introduced as defined in the Droplet Model with an attenuation factor given by [12,13]

The distortion αa is the root mean square of the deviation of the surface from a sphere, a quantity which incorporates all types of deformation indiscriminately. Using this approach, shell corrections only play a role near the ground state of the compound nucleus and not at the saddle-point.

To describe the continuous transition from one spherical nucleus to two tangent spherical nuclei [14,15].

c₁ and c₂ are the two radial elongations and a the neck radius. Assuming volume conservation, the two parameters s₁ = a / c₁ and s₂ = a / c₂ completely define the shape.

3. Fission Barriers

As with any other decay width, the fission width (Γ_f ) for an excited nucleus is determined by the product of the excited level spacing (Dc) and the sum of the transmission coefficients over all channels leading to fission [16]:

Most measurements of the fission cross sections were performed at energies above the fission barriers. Fission widths for such energies can be written in the form:

where ρ_c and ρ_f are the level densities for the equilibrium compound and saddle configurations, respectively, and B_f is the fission barrier height.

Generally, fission barriers are approximated by the equation:

where B_ld is the liquid-drop component of the fission barrier, δE₀ is the ground state shell correction, and δE_f is the corresponding shell correction for the saddle configuration of the fissioning nucleus.

Measured barriers for about 120 nuclei were fitted by the formula:

where S = A^2/3(1−kI²) is proportional to the nuclear surface energy with I = (N−Z)/A, and the surface symmetry coefficient k is defined as k = 1.9 + (Z − 80)/75. The fission parameter (X) is proportional to the ratio of the Coulomb and surface energies, and can be defined as [17]:

Function F is cubic, and joined smoothly to a straight line at X = X₁:

with X₀ = 48.5428 and X₁ = 34.15.

4. The Root Mean Square Radii

The mean-square radius is defined by [18-20]:

and the rms radius is the square root of this quantity denoted by

In the liquid-drop model the density is given by a constant density

The rms radius for this sharp-surface distribution is given by

The sharp-surface model could be improved when the surface allowed to be diffuse. This can be do with the Fermi distribution shape:

The rms radius is given by

Where . In the Fermi distribution model for A nucleons the interior density is given by:

For large A we neglect the  term, and if we assume that the rms radius for neutrons is the same as that for the protons then

5. Results

Figures 2 and 3 shows binding energies as a function of A. LDM calculations are in comparison with experimental data and the quantum molecular dynamic model calculations. We could see that there is a good agreement between LDM calculations and both experimental data and QMD model [21] as a theoretical calculations.

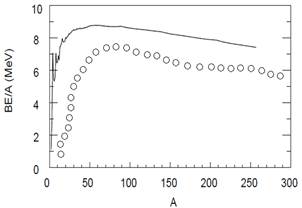
Fig. 2. Experimental values for the BE/A as a function of A for the most stable.

Nuclei (solid line). Liquid drop model calculations (open circles).

Fig. 3. The liquid-drop model for BE/A (closed circles). QMD model for BE/A ( open circles).

In Figure 4 the fission barriers is obtained. Liquid-drop models are plotted for ²³²Th and ²⁴⁰Pu. The barriers are plotted as functions of distance R₁₂ (in R₀ units) between the fission fragments.

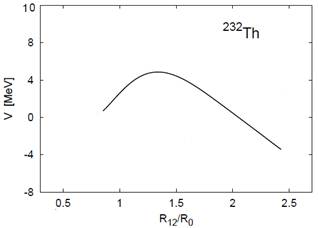
Fig. 4. Liquid-drop fission barriers for ²³²Th (top) and ²⁴⁰Pu (bottom).

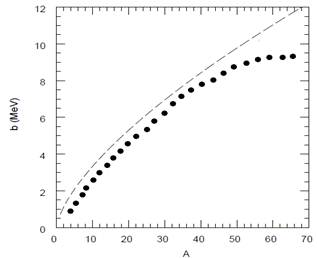
Fig. 5. b-coefficients for the isobaric mass multiplet equation. The closed symbols show the values obtained from experimental binding energies. The dashed line is the prediction of the liquid drop model.

In figure 5, The b coefficients obtained from the experimental binding energy are shown. They are compared with the prediction of the liquid drop model. The liquid drop model is always higher than experiment. The reason is that the observed displacement energy is related to a change in proton-neutron occupancy of the orbits near the Fermi surface which have an rms radius which is larger than the average rms radius implicit in the liquid drop model.

Figure 6 shows the probability density of ²⁰⁸pb which taken from ref. [22, 23 ]. If one were to put the 208 nucleons of ²⁰⁸Pb into a simple cubic lattice, a density of 0.16 nucleons/fm² corresponds to a lattice spacing of 1.85 fm. The data drawing Gaussian distributions for several nucleons each of which has an rms radius of 0.88 fm and which are spaced a distance of 1.85 fm. The data is compared with LDM and QMD model. We could see LDM gives more nice agreement with the data and the calculations of QMD model gives somewhat agreement with both LDM and the experimental data.

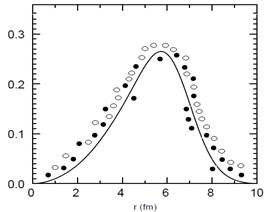
Fig. 6. Probability profile of ²⁰⁸pb (solid line ), liquid drop model calculations (open circles) and QMD model calculations (closed circles ).

In figures 7-10, the fusion cross sections of the nuclear reactions ⁹ Be + ¹⁴⁴Sm, ¹⁶ O + ¹⁶O, ⁴⁸ Ca + ⁹⁶Zr and ⁶⁴ Ni + ⁶⁴Ni are calculated using our LDM and the QMD model. In fact i decided to choose light, medium and heavy systems to see and get a general impression. As we could see there is a good agreement between both models, and in all cases the LDM calculation is higher than the results given by QMD. In figure 11, the LDM calculation for the rms radii as a function of the atomc number is presented. It's clear that the results is fitted as proportionality linear function.

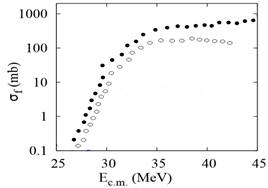
Fig. 7. Fusion cross section of ⁹ Be + ¹⁴⁴Sm. Liquid drop model calculations (closed circles) and QMD model calculations (open circles).

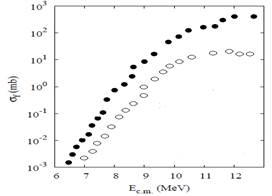
Fig. 8. Fusion cross section of ¹⁶ O + ¹⁶O. Liquid drop model calculations (closed circles) and QMD model calculations (open circles).

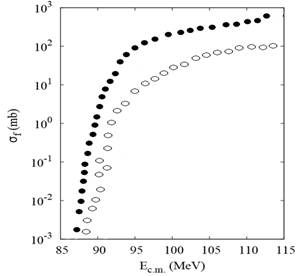
Fig. 9. Fusion cross section of ⁴⁸ Ca + ⁹⁶Zr. Liquid drop model calculations ( closed circles) and QMD model calculations ( open circles).

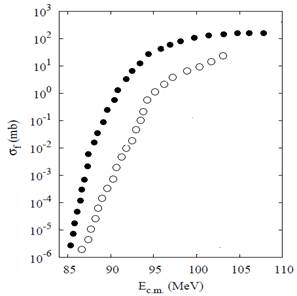
Fig. 10. Fusion cross section of ⁶⁴ Ni + ⁶⁴Ni. Liquid drop model calculations (closed square) and QMD model calculations (open circles).

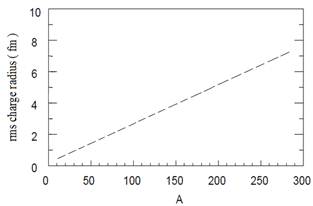
Fig. 11. Liquid drop model calculations for rms charge radii as a function of the atomic number.

6. Summary

Rotational Liquid-Drop Model with the volume, surface  and Coulomb energies is introduced to calculate many characteristics of nuclear reactions for light, medium and heavy systems. The binding energies as a function of the mass number for the most stable nuclei, liquid-drop fission barriers for some heavy nuclei, b-coefficients for the isobaric mass multiplet equation, probability profile of ²⁰⁸pb, fusion cross section of some nuclear reactions and root mean square charge radii as a function of the atomic number are calculated on the frame of LDM calculations. LDM calculations are compared with experimental results and QMD model calculations as well. The comparison was somewhat good and this is indicate that LDM is a good predication for all these characteristics.

References

1. C.F. von Weizsacker, Z. Phys. 96, (1935) 431.
2. H.A. Bethe and R.F. Bacher, Rev. Mod. Phys. 8, (1936) 82.
3. L. Meitner and O.R. Frisch, Nature London, 143, (1939) 239.
4. N. Bohr and J.A. Wheeler, Phys. Rev. 56, (1939) 426.
5. K. Pomorski and J. Dudek, Phys. Rev. C67 (2003) 044316.
6. Royer G.,Generalized Liquid Drop Model and Fission, Fusion, Alpha and Cluster Radioactivity and Super heavy Nuclei,Current Problems in Nuclear Physics and Atomic Energy, Kiev, Ukraine (2012)
7. Hofmann, S., Munzenberg, G., Rev. Mod. Phys. 72 (2000) 733.
8. Moretto, L.G., Physics and Chemistry of Fission, IAEA, Vienna, Vol. 1 (1974) 329.
9. Freiesleben, H., Britt, H.C., Huzenga, J.R., Physics and Chemistry of Fission, IAEA, Vienna, Vol. 1 (1974) 421.
10. Ignatyuk, A.V., Itkis, M.G., Okolovich, V.N., Smirenkin, G.N.,Tishin, A.S., Sov. J. Nucl. Phys. 21 (1976) 612.
11. Ignatyuk, A.V., Istekov, K.K., Smirenkin, G.N., Sov. J. Nucl. Phys. 30 (1979) 1205.
12. Dahlinger, M., Vermeulen, D., Schmidt, K.H., Nucl. Phys. A376(1982) 94.
13. Ignatyuk, A.V., et al., Sov. Part. Nucl. 16 (1985) 709.
14. Smirenkin, G.N., INDC(CCP)-359, IAEA, Vienna (1993).
15. Oganessian, Yu.Tc., Lazarev, Yu.A., Treatise on Heavy-Ion Science,Bromley, D. (Ed.), Vol. 4 (1987) 3.
16. Sierk, A.J., Phys. Rev. C33 (1986) 2039.
17. Myers, W.D., Swiatecki, W.J., Phys. Rev. C60 (1999) 014606.
18. Vigdor, S.E., Karwowski, H.J., Jacobs, W.W., Kailas, S., Singh,P.P., Soga, F. Throwe, T.G., Phys. Rev. C26 (1982) 1035.
19. Ignatyuk, A.V., Istekov, K.K., Smirenkin, G.N., Sov. J. Nucl. Phys. 36 (1982) 54.
20. Royer G., Remaud B. Static and dynamic fusion barriers in heavy-ion reactions, Nucl. Phys. (1985)Vol. A444, P. 477.
21. Kh Abdel-Waged, A Abdel-Hafiez and V V Uzhinskii,J. Phys. G: Nucl. Part. Phys. 26, No. 8 (2000) 1105.
22. Lecture Notes in Nuclear Structure Physics, B. Alex Brown, 2011.
23. Frégeau M. O. et al. X-Ray fluorescence from the element with atomic number Z = 120, Phys. Rev. Lett. (2012) Vol. 108, P. 122701.