The Group Theory as an Algebraic Approach for Prediction of Some Nuclear Structure Characteristics

A. Abdel-Hafiez^*

Experimental Nuclear Physics Department, Nuclear Research Center, AEA, Cairo, Egypt

Abstract

An algebraic model depends upon the group theory emphasizes the coherent behavior of all of the nucleons. Among the kinds of collective motion that can occur in nuclei are rotations or vibrations that involve the entire nucleus. In this respect, the nuclear properties can be analyzed using the same description that is used to analyze the properties of a charged drop of liquid suspended in space. The algebraic collective model can thus be viewed as an extension of the liquid drop model, the algebraic collective model provides a good starting point for nuclear structure and then one could understand fission. For that purpose I have discussed and calculated some characteristics as the energy per particle, charge distribution, energy spectra for nuclei. Also, the collective potential-energy as a function of the internuclear distance and the potential as a function of the control parameter could be explained successfully as well.

Keywords

Group Theory, Algebraic Collective Model, Nuclear Structure

Received: June 10, 2015
Accepted: June 25, 2015
Published online: July 16, 2015

@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/

1. Introduction

The ACM (algebraic collective model) [1–7] is an algebraic version of the Bohr model [8] based on a dynamical group SU(1, 1)×SO(5) for which all the matrix elements needed in applications of the model are calculated analytically. It is a development of the computationally tractable version of the collective model [2] that enables collective model calculations to be carried out efficiently by use of wave functions that span modified oscillator series of SU(1,1) irreps (irreducible representations) [9,10] and complementary SO(5) wave functions. Modified oscillator SU(1,1) irreps, used previously by Davidson [11] in molecular physics, give bases of wave functions in which the expansions of collective model wave functions for deformed nuclei are an order-of-magnitude more rapidly convergent than in a conventional harmonic oscillator basis. The method used in [2] for calculating model SO(5) wave functions was subsequently used [10] to develop an algorithm for computing SO(5) spherical harmonics and from them the SO(5) Clebsch-Gordan coefficients needed for a complete algebraic expression [4] of the Bohr model. It followed that, with access to the required SO(5) Clebsch-Gordan coefficients, there was no longer any need to calculate wave functions or carry out integrations in applications of the ACM because they could all be expressed in terms of given analytical SU(1,1) matrix elements and SO(5)-reduced matrix elements [4–6, 11]. Thus, the SU(1, 1) × SO(5) dynamical group structure of the ACM enables the effective, but computationally intensive, methods of Bohr model calculations in a conventional U(5) ⊃ SO(5) basis [12,13], as used in the Frankfurt code [14,15], to be avoided.

The algebraic collective model has been very successful in describing a variety of nuclear properties, especially energy levels in nuclei with an even number of protons and neutrons. These even nuclei can often be treated as having no valence particles so that the Shell Model does not apply [16,17]. These energy levels show the characteristics of rotating or vibrating systems expected from the laws of quantum mechanics. Commonly measured properties of these nuclei, including broad systematics of excited state energies, angular momentum, magnetic moments, and nuclear shapes, can be understood using the collective model [18]. The shell model and the collective model represent the two extremes of the behavior of nucleons in the nucleus. More realistic models, known as unified models, attempt to include both shell and collective behaviors.

The two most important developments in nuclear physics were the shell model and the collective model. The former gives the formal framework for a description of nuclei in terms of interacting neutrons and protons. The latter provides a very physical but phenomenological framework for interpreting the observed properties of nuclei. A third approach, based on variational and mean-field methods, brings these two perspectives together in terms of the so-called unified models. Together, these three approaches provide the foundations on which nuclear physics is based. They need to be understood by everyone practicing or teaching nuclear physics, and all those who wish to gain an understanding of the foundations of the models and their relationships to microscopic theory as given by recent developments in terms of dynamical symmetries.

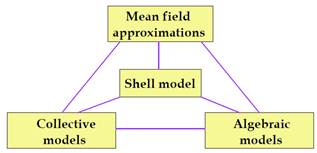
Fig. 1. Flowchart for how algebraic models create related to collective and shell models.

Some researches provided a simple presentation of the models and theory of nuclear collective structure, with an emphasis on the physical content and the ways they are used to interpret data. It also describes the extensions of these models to parallel unified models in which neutrons and protons move in a mean-field with collective degrees of freedom. The collective model (developed by Aage Bohr and Ben Mottleson), extends the liquid drop model by including motions of the whole nucleus such as quantized. Algebraic models is consider one of the mean field approximations and is related to both of the shell model and collective models by the way on figure 1. The harmonic oscillator shell model provides the formal framework for the description of nuclear structure. It is an exceedingly rich algebraic model with a wealth of dynamical subgroups chains and solvable submodels.

2. Theory

2.1. Derivation of the Hamiltonian for the Algebraic Collective Model

Bohr considers the radius of a liquid drop model nucleus expanded in quadrupolar spherical harmonics

          (1)

R₀ is the mean radius and  is a second order spherical harmonic with  and  the usual polar angles. The parameters then give the shape, restricted of course to only quadrupolar deformation. We will adopt an equivalent set of shape parameters, given by the quadrupole moments of the nuclear density [19].

               (2)

Where {q_m, m=0, ±1, ±2 }Rotate from the laboratory (space-fixed) coordinates q to an intrinsic (body-fixed) frame of principal axes with coordinates

                         (3)

where  is a five dimensional Wigner rotation matrix and  represents the three Euler angles relating the intrinsic frame to that of the laboratory. Introducing the variables b and g such that  and we can write the original coordinates in terms of these new variables

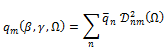
  (4)

From the definition of  , g is independent of the orientation and so gives the intrinsic shape, while the orientation is given by the three Euler angles W. Quadrupole deformations of a sphere yield ellipsoidal distributions, and Bohr shows [9] that gÎ[0,p/3] with g=0 for a prolate (rugby football shaped) nucleus and g=p/3 for an oblate (discus shaped) nucleus; (figure2). For intermediate values of g the nucleus is triaxial, that is, it has no axis of symmetry

The kinetic energy is proportional to the  Laplacian which in these coordinates is given by

         (5)

Where , .Where  is the quadratic SO(5) Casimir operator. are the SO(3) angular momentum operators in the intrinsic frame. SO(5) acts in  as orthogonal transformations that leave the magnitude b fixed. Thus SO(5) can affect only the shape coordinate g or the orientation W, and any potential independent of these coordinates must therefore be SO(5) invariant. SO(3) acts in  as a physical rotation of the nuclear distribution. Thus it affects only the orientation W, and since it leaves b fixed it is a subgroup of SO(5). The embedding of SO(3) in SO(5) is specified up to conjugacy by requiring the irreducible three dimensional SO(3) rotations of a distribution in  to induce an irreducible five dimensional SO(3) action upon the quadrupole space .

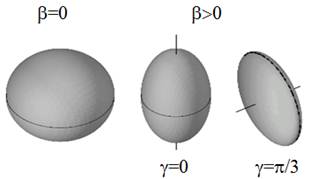
Fig. 2. Nuclear shape for various limiting values of the parameters b and g. The two deformed cases depicted with b > 0 have axial symmetry indicated by the axes.

Consider a nucleus with a spherical equilibrium shape that makes only small displacements in q. This is a five dimensional harmonic oscillator, since there are five independent modes of oscillation q_m. This is not to be confused with oscillations in physical 3-space we are in the space of quadrupole moments .

The Hamiltonian is that of a simple harmonic oscillator in the quadrupole coordinates

         (6)

where classically p^m=Bq^m. B is a mass parameter and w is an angular frequency, both independent of mode m. In practice these can be determined from experiments with nuclei that exhibit such vibrational spectra. In theory they can be computed using

hydrodynamical arguments in the liquid drop picture, although such calculations must be corrected for various single particle shell effects such as pairing.

We can make the usual transformation to boson creation and annihilation operators

 ,                                              (7)

With . These excitations are viewed as phonons each carrying angular momentum 2.

The Hamiltonian in equation (6) becomes

                     (8)

and in the algebraic collective model coordinates the Hamiltonian becomes

                     (9)

2.2. Algebraic Collective Model

The eigen functions of g-independent Hamiltonians can be classified according to the chain [20].

   (10)

where l labels a SU(1, 1) irreducible representation and  a basis. SU(1, 1) acts as scale transformations on the radial coordinate b, and SO(5) acts as orthogonal transformations in the space of quadrupole moments. The situation is analogous to that of a particle interacting with a central potential in real 3-space, such as an electron in a hydrogen atom where the symmetry group is SU(1, 1) ´ SO(3).  is the analogue of the principal quantum number and u is the analogue of the angular momentum quantum number.

The algebraic model adopts the SU(1, 1) ´ SO(5) decomposition of the Bohr model Hilbert space. Basis states, labelled according to the subgroup chain (1), are of the form

              (11)

The states {  , are a basis of an irrep  of SU(1,1). We include the subscript u on the SU(1,1) label because in our generalized basis these labels depend upon the seniority. The states {  are a basis for an irrep of SO(5). The  values appropriate for a state of seniority u are given by the SO(5)  SO(3) branching rule. Tensor products of these states therefore span a representation of the direct product group SU(1,1) ´ SO(5). We can give these states realizations in the collective coordinates {b,g,W}as

         (12)

 is a radial wave function and  is a hyperspherical harmonic.

For a particle of mass m in under the influence of a central potential V (r) the Hamiltonian is

                         (13)

Where  is the Laplacian on  . In spherical coordinates we have

                     (14)

Where  is the quadratic SO(3) Casimir operator

       (15)

The Hamiltonian  is rotationally invariant, i.e., it has static SO(3) É SO(2) symmetry and solutions are labeled with the two quantum numbers . The wave functions are separable  and the functions  which satisfy the eigenvalue equation

           (16)

are the spherical harmonics. The standard definition has

          (17)

where  is an element of the coset space SO(3) / SO(2) and is a Wigner –function [14].

2.3. Algebraic Collective Shape Phase Transition Potential

In this part we investigate of deformation in the Bohr collective model by studying a spherical vibrator to soft rotor shape phase transition. The general Hamiltonian of a system exhibiting a transition is of the form

                     (18)

where a is the tunable parameter. The two non-commuting Hamiltonians  possess different dynamical symmetries, each corresponding to a phase of the system.

Using equation (9) we get

                 (19)

where we've included a unit of quadrupole length b. From equation (18), the phase transition Hamiltonian is therefore

        (20)

Where  is the  Laplacian of equation (5), B is a collective mass parameter, and

is a vibrational angular frequency. It will be convenient to set  equal to 1

and write B = M B₀, so that the mass parameter M is dimensionless, and to set the unit

of energy. The Hamiltonian then becomes

               (21)

Then the phase transition potential is

                          (22)

This phase transition potential exhibits a critical point a=0.5 at which the coefficient of the b² term vanishes. For a £ 0.5 the minimum is at b=0, while for a > 0.5 it is b = [(2a-1)/2a]^1/2.

2.4. The Collective Model Wavefunctions

We give the ground state  itsproper time development

                            (23)

and its density distribution

        (24)

Consider the time-dependent wave function

            (25)

for infintismal , where  is an excited eigenstate of the nucleus. The density distribution for this time-dependent wave function, unlike that for a stationary state, oscillates harmonically about its ground state distribution

      (26)

Where  is the transition density

            (27)

Now  is a good time-dependent wave function for the Hamiltonian. Thus it follows that the motion is not damped, it cannot lose its energy to any other mode, and it is therefore meaningfully described as a normal oscillation.

3. Results and Discusions

The energy per particle as a function of density for symmetric nuclear matter is shown in Fig.3 we noticed that the energy per nucleon is negligible for low densities and become more and more significant as the densities increases.

The symmetry energy is defined from the energy per nucleon E/A as follows

 where  is the so called asymmetry parameter and . In Fig. 4 we show the results for the energy per particle in the case of a system composed of neutrons only. We find that E/A is sharply increasing at very high densities. In Fig.5 Charge distribution of ²⁰⁸pb is calculated in comparison with experimental data, we could see that there is a great agreement between my calculations and the given experimental data.

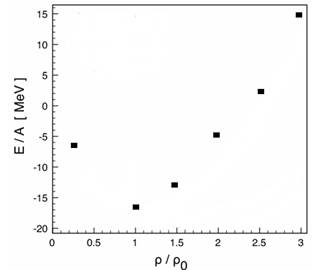
Fig. 3. Energy per particle in symmetric nuclear matter as a function of density (in units of the nuclear saturation density r₀ = 0.16 fm^-3).

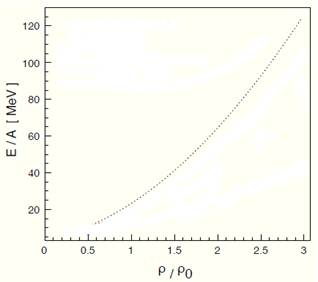
Fig. 4. Energy per particle in neutron matter as a function of density (in units of the nuclear saturation density r₀ = 0.16 fm⁻³)

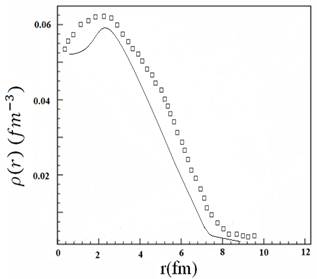
Fig. 5. Charge distribution of ²⁰⁸pb. The experimental charge distribution(open square ) is that of Ref. [21].

The tendency of particles to couple pairwise to zero spin configurations has been recognized for a long time for the following reasons:

(i)      Even-even nuclei invariably have zero spin ground states.

(ii)     The low-lying spectra for even-even nuclei are particularly simple. There is an energy gap corresponding to the energy required to break a zero spin pair, below which only collective states appear. Figure 6 contrasts the spectra for some typical neighbouring even-even, even-odd, and odd-odd nuclei.

(iii)   The last nucleon is less strongly bound in an odd-mass nucleus than in the neighbouring even-even nuclei, where it can form part of a pair.

Figure 7 shows the ¹²C + ¹²C nuclear molecule along with the collective potential energy landscape as a function of the internuclear distance and the alignment between the two deformed nuclei. The potential curves are presented for fixed orientation of the two ¹²C intrinsic symmetry axis relative to the internuclear axis, the three axes being coplanar.

Figure 8 shows a plot of the phase transition Potential as a function of the transition parameter a which clearly shows the emergence of a potential well for a > 0.5. This well serves to stabilize a nonzero mean value of b and so gives rise to deformation.

Fig. 6. Energy spectra for neighboring even-even, even-odd and odd-odd nuclei.

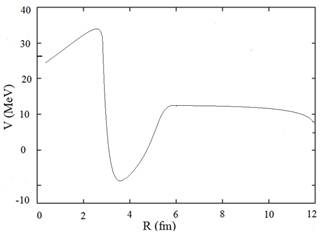
Fig. 7. The collective potential-energy landscape for the ¹²C + ¹²C nuclear molecule as a function of the internuclear distance and alignment, V(R, θ1, φ1 = 0, θ2, φ2 = 0).

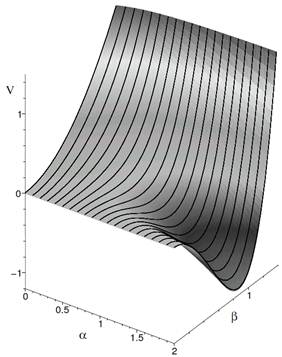
Fig. 8. The potential as a function of the control parameter a. A critical point is reached as a passes through 0.5, whereafter there is a well about b = [ (2a-1)/2a]^1/2.

4. Conclusion

I have presented an algebraic collective model and illustrated its utility in several nuclear structure calculations. The purpose of my calculations was not only to find agreement with any particular experiment, but also to refine the Bohr model so that it can be brought to bear on a wider class of topics currently of interest. The results from our investigation indicate that the collective model has more to contribute to nuclear structure physics than might have been thought.

I have presented the energy per particle in both symmetric nuclear matter as function of density and in neutron matter as a function of density. At high densities the nucleon spectral function is modified significantly. Also, Charge distribution of ²⁰⁸pb could be calculated. Energy spectra for neighboring even-even, even-odd and odd-odd nuclei could be explained. The collective potential-energy landscape for the ¹²C + ¹²C nuclear molecule as a function of the internuclear distance and The potential as a function of the control parameter could be explained successfully as well.

References

1. M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions, (Dover Publications, New York, 1968).
2. D.J. Rowe, Nucl. Phys. A735, 372 (2004).
3. D.J. Rowe, Nucl. Phys. A745, 47 (2004).
4. D.J. Rowe and P.S. Turner, Nucl. Phys. A753, 94 (2005).
5. D.J. Rowe, J. Phys. A: Math. Gen. 38, 10181 (2005).
6. D.J. Rowe, T.A. Welsh, and M.A. Caprio, Phys. Rev. C79, 054304 (2009).
7. D.J. Rowe and J.L. Wood, Fundamentals of Nuclear Models; Foundational Models (World Scientific, Singapore, 2010).
8. A. Bohr and B.R. Mottelson, Nuclear Structure Vol. 1: 1969, Vol. 2: 1975 (Benjamin, New York and Reading, Mass.; republished by World Scientific, Singapore, 1998).
9. A. Bohr, Mat. Fys. Medd. Dan. Vid. Selsk. 26, no. 14 (1952).
10. D.J. Rowe, P.S. Turner, and J. Repka, J. Math. Phys. 45, 2761 (2004).
11. M.A. Caprio, D.J. Rowe and T.A. Welsh, Comput. Phys. Commun. 180, 054304 (2009).
12. J. Cizek and J. Paldus, Int. J. Quant. Chem., XII, 875 (1977).
13. T.H. Cooke and J.L. Wood, Am. J. Phys. 70, 945 (2002).
14. A.R. Edmonds, Angular Momentum in Quantum Mechanics, 2nd ed. (Princeton University Press, New Jersey, 1960).
15. C.L. Jiang et al, Phys. Rev. Lett. 110, 072701 (2013).
16. E. Cha´con, M. Moshinsky and R.T. Sharp, J. Math. Phys. 17, 668 (1976); E. Cha´con and M. Moshinsky, J. Math. Phys.18, 870 (1977).
17. J.M. Eisenberg and W. Greiner, Nuclear Models, 3rd ed. (North-Holland, Amsterdam, 1987).
18. P.O. Hess, J. Maruhn and W. Greiner, J. Phys. G7, 737 (1981); D. Troltenier, J.A. Maruhn and P.O. Hess, in: Computational Nuclear Physics 1, eds. K. Langanke, J.A. Maruhn and S.E. Koonin (Springer, Berlin, 1991).
19. D. J. Rowe, Prog. Part. Nucl. Phys. 37 (1996), 265.
20. Peter Shipley Turner, The Algebraic Collective Nuclear Model and SO(5), Ph. D. thesis,Graduate Department of Physics University of Toronto, 2005.
21. D. Vautherin and D.M. Brink, "Hartree-Fock Calculations with Skyrme’s Interaction. I. Spherical Nuclei", Phys. Rev. C 5, 626 (1972)