Speckle Correlation Fringes Phase Extracted by Spiral Phase Transform from Bidimensional Empirical Mode Decomposition
R. Rhanim, A. Gholaifan, V. Dembele, K. Assid, A. Nassim*
Instrumentation Measure and Control laboratory, Chouaib Doukkali University, Sciences Faculty, El Jadida, Morocco
Abstract
In this paper, we propose a 2D phase extraction algorithm to retrieve optical phase from a single correlation fringe pattern by employing the Bidimensional Empirical Mode Decomposition (BEMD) followed by the Spiral Phase Transform (SPT). The SPT transform extracts the modal phase from every BIMF which is a zero mean 2D AM–FM component obtained by BEMD decomposition, and then the total phase is computed adding all modal phases. The first BIMF of speckle correlation fringe pattern is dominated by residual speckle noise. Hence, the speckle noise can easily be removed by just skipping the first BIMF. The employ of the BEMD decomposition allowed generating an exact quadrature fringe pattern, and then generates a good accuracy in phase extraction by SPT. Numerical simulation study demonstrate the validity of the proposed method and real fringe patterns of carbon fiber deformation gives results in close agreement with those produced by the phase shifting method.
Keywords
Phase Extraction Methods, Spiral Phase Transform SPT, AM-FM Model, Bidimensional Empirical Mode Decomposition BEMD, Speckle Correlation Fringes
Received:May 18, 2015
Accepted: May 29, 2015
Published online: July 9, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
Many interferometry optical techniques provide the measurement data codified in fringe pattern as the phase of a periodic intensity profile. It has become one of the principal world-wide research topics of optical metrology and considered as a powerful tool for industrial measurements. The fringe pattern analysis consists of the phase evaluation methods [1,2] employed to measure various physical magnitudes. The developments of more sophisticated phase evaluation algorithms are continuously needed [3-6].
In this paper, we consider a 2D phase extraction algorithm to retrieve the phase from a single fringe pattern by employing the Spiral Phase Transform (SPT) and the BEMD decomposition. The SPT transform extracts the modal phase from every BIMF which is 2D AM–FM component obtained by BEMD decomposition, and then the total phase is computed from the sum of modal phases. The SPT transform is the complex Riesz transform introduced by Larkin [7,8] and has been pointed out in different studies such as analysis of fringe pattern [9-11] and recently for speckle patterns analysis [12]. It is an extension of the Hilbert transform in higher dimensions.
The employ of the BEMD decomposition allowed generating an exact quadrature fringe pattern. It was developed to minimize the specific limitations set by the Bedrosian-Nuttall theorems and has helped to overcome many of the difficulties of the regular Hilbert transform. The comprehensive review can be found in [13]. The Empirical Mode Decomposition EMD was introduced by Huang [14] for one dimensional data and then extended to images [15] under the name Bidimensional Empirical Mode Decomposition BEMD. The BEMD decompose an image into a set of images called Bidimensional Intrinsic Mode Function BIMF and a residue. Adding all the BIMFs with the residue reconstructs the original image without distortion or loss of information.
In this study, we consider the speckle correlation fringe pattern that arises in the context of Digital speckle pattern interferometry DSPI [16,17] where the displacement fields is obtained digitally by subtracting two speckle images recorded before and after deformation. The speckle [18] which is a granular structure resulting from the self-interference of a coherent waves randomly scattered from a rough surface, is used for the measurement of displacements with accuracy of order of wavelength.
The proposed method is validated by numerical simulation study and then applied to real fringe patterns of carbon fiber deformation which are compared to Wyant-Phase Shifting algorithm which is based on four π/2 shifted images.
In order to generate the speckle patterns diffracted by a surface, we simulate the clean imaging optical system [19] as an out of plane interferometer. Within the paraxial approximation, optical propagation through any complex optical system, described by an ABCD ray transfer matrix, can be formulated by Collins formulas [20]. Collins has obtained an analytic form for the resulting complex field amplitude.
To provide a continuous phase distribution over its definition domain, an unwrapping procedure must be applied. We used in this work, a fast phase unwrapping algorithm [21] to unwrap the extracted phase by SPT.
The paper is organized as follows. Section 2 is devoted to a presentation of the Spiral Phase Transform applied to 2D AM-FM model. In this section, we expose the Bidimensional Empirical Mode decomposition BEMD to extract BIMF modes which are 2D AM-FM components and the Spiral Phase Transform. In section 3 we present results from simulated speckle correlation fringes for the validity of the method and results of carbon fiber deformation study. Finally, a conclusion is presented in section 4.
2. Phase Extraction Technique by SPT from BIMF Mode
2.1. Bidimensional Empirical Mode Decomposition BEMD
The Bidimensional Empirical Mode Decomposition BEMD is an extension of the Empirical Mode Decomposition EMD introduced by Huang [14] for one dimensional data. Details of the BEMD concept are fully available in [15]. The BEMD technique extracts, directly from the data a finite number of zero-mean 2D AM–FM components, called Bidimensional intrinsic mode function (BIMF). The BEMD acts as filter bank and decompose an image into a set of images or BIMFs obtained by sequential extraction of frequency modes associated with various intrinsic space scale of the image starting from the high frequency modes to low ones. Each BIMF has two specific properties [22]: the same number of zero-crossings and extrema, and also has symmetric envelopes defined by the local maxima, and minima, respectively. Each BIMF component is extracted by the sifting process and representing the fast fluctuating and the residue component representing a slower fluctuating. The same sifting is then applied to the residue as new input to extract the next BIMF and produce a new residue. Ideally the last residue should stand for the DC component or bias of the original image data. The total sum of the BIMFs with the residue matches the image very well and therefore reconstructs the original image without loss of information. The sifting process depends on how to detect local extrema, how to interpolate scatter data points, and what stopping criteria to use.
In this paper we have used neighboring window to detect the image extrema and thin-plate spline RBF (radial basis function) to compute the surface interpolation [23]. Extremas points are extracted by comparing the candidate data point with its nearest 8-connected neighbors. An extension of the image adding extra data points permit the determination of extremas at the borders. Stopping criteria controls the number of iterations thus balancing performance versus computation time. We have limited the size of the standard deviation SD [24] to guarantee that each BIMF component retain enough physical sense of both amplitude and frequency modulations.
2.2. Spiral Phase Transform
The Spiral phase Transform noted SPT is the complex Riesz transform which is an extension of the Hilbert transform in higher dimensions introduced by Larkin and has been used in different studies such as analysis of fringe pattern and speckle patterns analysis. The SPT operator corresponds mathematically to
![]() (1)
(1)
Where f is an input image, (x,y) are the pixel coordinates. FT means 2D Fourier transformation (resp. FT-1 means 2D Fourier inverse transformation), j denotes complex operator which obey the following rules j2= -1 and h is the spatial spiral phase kernel function defined as
![]() (2)
(2)
In Fourier space, the spiral phase kernel expressed in frequency coordinates (u,v) is given by
![]() (3)
(3)
The spiral phase kernel can also be interpreted as the complex sum of two 2D Riesz kernels Rx and Ry which are the imaginary and real components of spiral phase kernel h, respectively given by
![]() (4)
(4)
The spiral phase operator has the following effect on the BIMF mode as
![]() (5)
(5)
The phase is an unknown quantity and therefore, it is not possible to determine the direction map η defined as [10]
![]() (6)
(6)
Instead of the direction map η, we can obtain the orientation map θ as
![]() (7)
(7)
That orientation map θ and direction map η are related by the following expression as
![]() (8)
(8)
The modal phase extracted by SPT from BIMF which are a zero-mean 2D AM–FM component affected by the local sign ambiguity is given by
![]() (9)
(9)
3. Results
3.1. Numerical Simulation
The simulation consists in generating numerically speckle correlation fringes of a given phase change resulting from surface displacement. This simulation computed by MATLAB, permits to verify the ability of our method to extract the phase distribution.
Speckle correlation fringes are obtained by subtraction of a reference speckled image from image of displaced surface. The intensity distribution of speckle correlation fringes is given by
![]() (10)
(10)
Where, b0 is a visibility function. The terms φ and φs are the phase (or test phase) change in the light resulting from the displacement and the original phase from the speckle that appears as the high frequency and apparently random pixel-by-pixel intensity variation, respectively. The test phase function we used is
![]() (11)
(11)



(a) (b) (c)




(d (e) (f) (g)
Fig. 1. (a) Simulated spee correlation fringes and (b) to (g) their BIMFs obtained by BEMD decomposition.
In Fig.1 we illustrate the simulated speckle correlation fringes and their BIMFs obtained by BEMD decomposition. The original image can be obtained by adding all BIMFs and residue. We noted that the first BIMF (finest mode) contains all the residual speckle noise which can be removed by just skipping this first BIMF and The DC component of the correlation fringe pattern is contained in the last BIMF that is the residue [25,26].




(a) (b) (c) (d)
Fig. 2. The modal phases extracted by SPT from each BIMF.

Fig. 3. The wrapped phase obtained by adding all modal phases.
In Fig.4 we present the unwrapped retrieved phase and the test phase. To judge the unwrapped retrieved phase image quality assessment, we use the SSIM index (Structural Similarity) [27,28] that compares local patterns of pixel intensities that has been normalized for luminance and contrast. In the spatial domain, the SSIM index between two patches x and y (an image with its reference) is defined as
![]() (12)
(12)
where μ and σ are the sample mean, standard deviation and covariance terms of x, y and xy, respectively, and C1 and C2 are two small positive constants to avoid instabilities. The maximum value 1 is achieved if and only if the image is similar to its reference. The comparison between the unwrapped phase and the test phase give the SSIM value equal to 0.937 which demonstrated the agreement of the method.
To emphasize the speckle size effect on this technique, we conducted a series of DSPI simulations for different average speckle sizes [29]. The results are presented in Table 1. In all the cases of large average speckle sizes, we have found a good agreement.
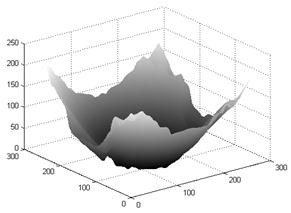
(a)
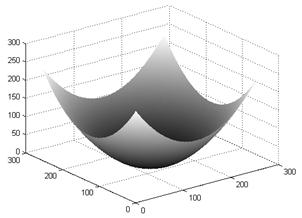
(b)
Fig. 4. (a) The unwrapped retrieved phase and (b) the test phase.
Tab. 1. SSIM values for different average speckle sizes.
| Speckle size (pixels) | SSIM |
| 1 | 0.937 |
| 2 | 0.935 |
| 3 | 0.932 |
| 4 | 0.930 |
3.2. Experimental Results
The performance of our algorithm was tested on real speckle correlation fringes of carbon fiber provided by 4D Technology, which depicted the deformation realized by pushing with a micrometer the center of the carbon fiber target toward the interferometer. The carbon fiber deformation fringes and their BIMFs obtained by BEMD decomposition are presented in Fig.6. From each BIMF, the modal phase is extracted by SPT and illustrated in Fig.7. The first mode and the last mode were removed where the residual speckle noise and the DC component are localized respectively.


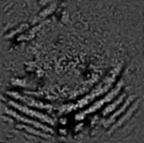
(a) (b) (c)

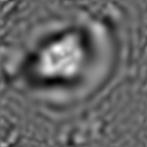


(d) (e) (f) (g)
Fig. 5. (a) Carbon fiber deformation fringes and (b) to (g) their BIMFs obtained by BEMD decomposition.




(a) (b) (c) (d)
Fig. 6. The modal phase extracted by SPT from each BIMF.

Fig. 7.. The wrapped retrieved phase obtained by adding all modal phases.
The wrapped retrieved phase obtained simply by adding all modal phases is presented in Fig.8. The unwrapped retrieved phase and phase extracted by phase-shifting method are illustrated Fig.9. Our extracted phase is in close agreement with those produced by the phase-shifting method.

(a)

(b)
Fig. 8. (a) The unwrapped retrieved phase and (b) phase extracted by phase-shifting method.
4. Conclusion
In this work we present a method to extract the optical phase from speckle correlation fringes. This algorithm which performed BEMD decomposition followed by Spiral Phase Transform, was validated on simulated correlation fringe and tested on real fringes of carbon fiber deformation. The proposed method can effectively extract with a good accuracy the phase distribution from a single speckle correlation fringes contaminated by a strong residual speckle noise. The obtained results are in close agreement with those produced by the phase-shifting method.
Acknowledgments
The authors want to thank Dr. Neal Brock and Dr. J. C. Wyant from 4D Technology for providing them the experimental shifted fringe patterns. The Bidimensional Empirical Mode Decomposition BEMD software was provided by Anna Linderhed: http://www.icg.isy.liu.se/~anna/emdcoding.html.
References
- S. Sirohi and S. Chau, ‘Optical Methods of Measurement’, Marcel Dekker, New York, NY, USA (1999)
- B. V. Dorrio and J. L. Fernandez, ‘Phase-evaluation methods in whole-field optical measurement techniques’, Measurement Science and Technology, vol. 10, no. 3, pp. R33–R55 (1999)
- MS. Tageda, S. Kobayashi, ‘Fourier transform methods of fringe pattern analysis for computer based topography and Interferometry’, Opt. Soc. Am, Vol. 72, pp.1156-1160 (1982)
- M. Afifi, FA. Fassi, M. Marjane, K. Nassim, M. Sidki, S. Rachafi, ‘Paul wavelet based algorithm for optical phase distribution evaluation’, Opt Commun, Vol. 211, pp. 47-51 (2002)
- K. Creath, ‘Phase – measurement interferometry techniques’, In Wolf E (ed.): Progress in optics Vol. XXVI. pp. 349–393 Elsevier Science, Amsterdam (1988)
- K. Assid, F. Alaoui, V. Dembele, S. Houmairi, M. Sidki, A. Nassim, ‘Normalized Hilbert Huang Transform-NHHT applied to Phase extraction in Wavelet Domain’, The Open Optics Journal.Vol.6, pp 9-13 (2012)
- K. G. Larkin, D. J. Bone, and M. A. Oldfield,‘Natural demodulation of two- dimensional fringe patterns. I. General background of the spiral phase quadrature transform’, J. Opt. Soc. Am. A 18, 1862–1870 (2001)
- K. G. Larkin,‘Natural demodulation of two-dimensional fringe patterns. II. Stationary phase analysis of the spiral phase quadrature transform’, J. Opt. Soc. Am. A 18, 1871–1881 (2001)
- J. Villa, I. De la Rosa, G. Miramontes, and J. A. Quiroga, ‘Phase recovery from a single fringe pattern using an orientational vector-field-regularized estimator’, J. Opt. Soc. Am. A, 22, 2766–2773 (2005).
- J. Vargas, R. Restrepo, J. C. Estrada, C. O. S. Sorzano, Yong-Zhao Du and J. M. Carazo, ‘Shack–Hartmann centroid detection using the spiral phase transform’, Applied Optics, Vol. 51, No. 30, 20 October (2012)
- M. Trusiak, K. Patorski, and M. Wielgus, ‘Adaptive enhancement of optical fringe patterns by selective reconstruction using FABEMD algorithm and Hilbert spiral transform’, Opt. Express 20, 23463-23479 (2012)
- Wei Wang, T. Yokozeki, R. Ishijima, A. Wada, Y. Miyamoto, M. Takeda, S. G. Hanson, ‘Optical vortex metrology for nanometric speckle displacement measurement’, Opt. Express 14, 120–127 (2006).
- N.E. Huang, Z. Wu, ‘A review on Hilbert-Huang transform: Method and its applications to geophysical studies’, Geophys 2008; RG2006, 23PP
- N.E. Huang, Z. Shen, S.R. Long, M.C. Wu, H.H. Shih, Q. Zheng, N.C. Yen, C.C. Tung, H.H. Liu, ‘The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis’, Proceedings of the Royal Society London, Part A 454 903–995 (1998)
- J.C. Nunes, Y. Bouaoune, E. Delecheslle, O. Niang, P. Bunel, ‘Image analysis by bidimensional empirical mode decomposition’, Image and Vision Computing 21 (November) 1019–1026 (2003)
- J. N. Butters and K. A. Leendertz, ‘Speckle pattern and holographic techniques in engineering metrology’, Meas. Control, 4, 349-354 (1971)
- J. W. Goodman, ‘Laser Speckle and Related Phenomena’, Vol. 9 of Topics in Applied Physics, Springer-Verlag, Berlin (1975)
- R. Jones and C. Wykes, ‘Holographic and Speckle Interferometry’, 2nd ed. Cambridge U. Press, Cambridge, England (1989)
- H.T. Yura, S.G. Hanson, J Opt Soc Am A 1987; 4:1931.
- S.A. Collins, J Opt Soc Am 1970; 60:1168–77.
- M.A. Schofield and Y. Zhu, ’Fast phase unwrapping algorithm for interferometric applications’,Optics Letters, Vol. 28, No. 14, July 15 (2003)
- A. Linderhed, ‘Image Empirical Mode Decomposition: a New Tool for Image Processing’, Advances in Adaptive Data Analysis 1(2), pp. 265-294 (2009)
- A. Linderhed, ‘Variable sampling of the empirical mode decomposition of two-dimensional signals’, Int. J. Wavelets Multiresolution Inf. Process. 03(03), 435–452 (2005)
- N.E. Huang, ‘Beyond the Fourier transform: coping with nonlinear, nonstationary time series’, NASA Goddard Space Flight Center, USA, 28 pp. http://www.Physiconet.org/events/hrv-2006/huang.pdf (accessed 26 May, 2006)
- M. B. Bernini, A. Federico and G. H. Kaufmann, ‘Noise reduction in digital speckle pattern interferometry using bidimensional empirical mode decomposition’, Appl. Opt. 47(14), 2592–2598 (2008)
- K. Assid, V. Dembele, F. Alaoui, and A. Nassim, ‘Bidimensional empirical mode decomposition BEMD applied to speckle denoising for wavelet phase evaluation’, Physical Chemical News, vol. 61, pp. 17–23, (2011)
- Z. Wang and A. C. Bovik, ‘A universal image quality index’, IEEE Signal Process. Lett., vol. 9, no. 3,pp. 81–84, Mar. (2002)
- Z. Wang, A.C. Bovik, H.R. Sheikh, E.P. Simoncelli, ‘Image quality assessment: from error visibility to structural similarity’, IEEE Trans. Image Processing, vol. 13, n. 4, pp. 600–612, apr. (2004)
- E. M. Barj, M. Afifi, A. Idrissi, S. Rachafi, A. Nassim,’Speckle Correlation Fringes Denoising using Stationary Wavelet Transform: Application in Wavelet phase evaluation technique’, Optics and Laser Technology, Vol. 38, issue 7, pp 506-511 (2006)



