A Computed Solution to the Schrödinger Equation in the One-Dimensional Non-Relativistic Electron Case Using a Polynomials Expansion Scheme

Ayşe Yumak¹, Karem Boubaker^{2, *}

¹Physics Department, Faculty of Arts and Sciences, Marmara University, Istanbul, Turkey

²Unity of Physics of Semi-Conductings Disposals UPDS, Tunis EL MANAR University, Tunisia

Abstract

In this paper, travelling wave solutions to the nonlinearly dispersive Schrödinger equation are computed in the case of one-dimensional non-relativistic electron confined to a cylindrical quantum well. Investigations gave evidence to the possibility of simplified continuous solutions which are in good agreement with the probabilistic interpretation of this equation.

Keywords

Schrödinger Equation, Non-Relativistic Electron, Quantum Well, Boubaker Polynomials Expansion Scheme BPES, Rogue-Langmuir Traveling Wave

Received: March 1, 2015 / Accepted: March 21, 2015 / Published online: May 5, 2015

@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/

1. Introduction

The well-known nonlinearly dispersive Schrödinger equation [1-8], described as:

              (1)

where is the unknown function which determines the probability distribution,  is a given parameter and m and n are positive integers and denote the intensity of the nonlinear term. This equation arises in a large number of mathematical and engineering problems such fluid mechanics, solid state physics, optic, chemical physics and plasma physics [5-12]. They also successfully represent an important class of nonlinear equations with many applications in updated physical sciences. i. e. for describing pulse propagation with equal mean frequencies in bi-refringent nonlinear fibres.

Exact and analytical solutions for nonlinearly dispersive Schrödinger equation have attracted considerable attention [9-16]. Nevertheless, most of provided standard results of boundary value problems for the nonlinear Schrödinger equation studies were not sufficient to investigate finite geometry configurations since coefficients of the differential equations have been usually chosen such as bounded and measurable functions. Several attempts yielded in this context, families of exact analytical solutions which were obtained using elementary functions [11-14].

 In the present work, a polynomial expansion scheme is performed in order to obtain Rogue-Langmuir-type traveling wave solution to Eq. (1). This paper is organized as follows. In Section 2, the resolution protocol is presented along with the studied system patterns.. In Section 3, plots of the are shown ad discussed. Last section is the conclusion.

2. Resolution Protocol

Schrödinger’s equation is introduced here in the case of a one-dimensional non-relativistic electron e^-of mass m, moving inside a cylindrical quantum well (C) of radius R (Fig. 1).

The potential in the whole space is defined as:

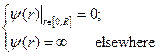     (2)

The situation is such as there is an infinitely high R-radius cylindrical surface at r = R zone .

Schrödinger’s equation in cylindrical co-ordinate system for the non-relativistic electron in quantum well is:

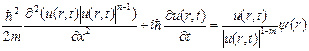 (3)

where  represents the probability of finding the electron anywhere .

As long as the purpose consists of yielding a Rogue-Langmuir traveling wave solution, an intermediary wave variable is introduced so that:

                             (4)

Consequently it comes that:

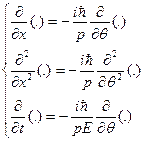            (5)

It comes, for n = 2 and m = 3, that Eq. (1) alters to:

 (6)

According to the problem geometry, we have the trivial condition. Consecutively, and starting from the formulation of the Boubaker Polynomials Expansion Scheme BPES [17-33], the expression of the unknown term of the traveling wave solution is proposed as following:

        (7)

where are the 4k-order Boubaker polynomials, are minimal positive roots [19-36],  is a prefixed integer, and  are unknown pondering real coefficients.

According to precedent studies [22-32], Boubaker Polynomials Expansion Scheme BPES protocol ensures validity of spatial boundary conditions prime to the resolution of the main equation.

This particularity of the protocol has been confirmed earlier by Barry et al. [30], Agida et al. [31], Yildirim et al. [32], Kumar [33], Fridjine et al. [34] and Benhaliliba et al. [35]. In fact these patterns were based on the properties of the Boubaker polynomials [19-33]:

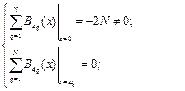           (8)

and:

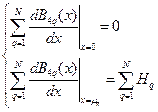                (9)

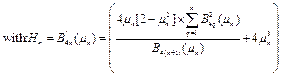
By combining the formulation Eq.(6) and that of Eq.(6), we obtain,  for the given potential expression in Eq. (2):

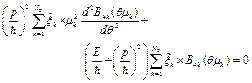 (10)

The BPES solution is obtained by determining the non-null set of coefficients  that minimizes the absolute fuctional :

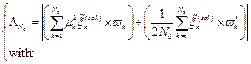  (11)

and

Finally the solution of Eq. (3) is:

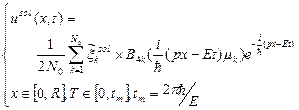  (12)

3. Computed Solution Plots and Patterns

Figure 2 shows plots of the obtained solution, for increasing values of  (and), while Figure 3 corresponds to the convergent solution modulus, obtained for . All the solutions have been represented with  and as space and time ranges, respectively.

It may be appropriate to point out that Eq. (3) is derived for short amplitude quasi-stationary slow motion describing the Rogue-Langmuir pondero-motive force. Most of classical solutions, which describe a classical-type particle motion under the action of such forces, consist of linear sums of wave functions corresponding to different energies [39,40] . The present solution accounts for the trapping of such waves in an infinite well, and oppositely to many other results, it concentrates the electron energy into a small region near at the vicinity of the central zone (Fig.4). This paradox can be explained by the nonlinear properties of the medium as well as the abrupt potential discontinuity at the envelop r=R.

Figure 4 presents the probability distribution within the cylinder (C). It monitors a typical single energy wave function having a static probability distribution in good agreement with the results of Banica et al. [1], Bégout et al. [2], Nadin [4], Gui et al. [3], Liu [41], Liang et al. [42-43] and Khang et al. [41].

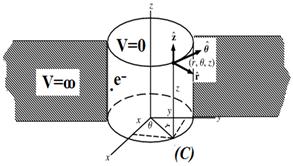
Figure 1. Non-relativistic electron moving inside a cylindrical quantum well

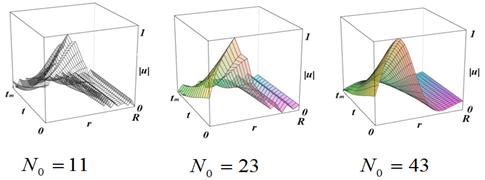
Figure 2. Solution convergence patterns (plots for and)

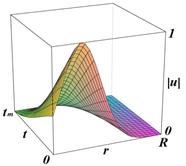
Figure 3. Convergent solution plots for

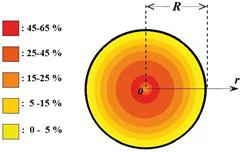
Figure 4. Probability distribution ()within the cylinder (C)

4. Conclusion

In this paper, we have proposed piecewise continuous and uni-modal Rogue-Langmuir-type traveling wave solution to the well known Schrödinger equation. The performed polynomial scheme has ensured the verification of boundary condition in advance to resolution process. The obtained solutions have been expressed in terms of wave function modulus and presented the singular advantage of imposing no quantification for both particle momentum and energy oppositely to most classical solutions. The convergence of the protocol has been discussed and enhanced accordingly.

References

1. V. Banica, L. Vega, Annales de l'Institut Henri Poincare (C) Non Linear Analysis, 25( 4) (2008), 697
2. P. Bégout, Jesús I. Díaz , Annales de l'Institut Henri Poincare (C) Non Linear Analysis, 29(2012) 35
3. C. Gui, M. Zhao, Annales de l'Institut Henri Poincare (C) Non Linear Analysis, Available online 9 May 2014, ISSN 0294-1449, http://dx.doi.org/10.1016/j.anihpc.2014.03.005.
4. G. Nadin, Critical, Annales de l'Institut Henri Poincare (C) Non Linear Analysis, Available online 9 May 2014, ISSN 0294-1449, http://dx.doi.org/10.1016/j.anihpc.2014.03.007
5. T. A. Davydova, A. I. Fishchuk, Ukrainian J Phys 1995;40:487-94.
6. T. A. Davydova, A. I. Fishchuk, Phys Scripta 1998;57:118-26.
7. Y. F. Chen, C. Y. Wang, S. H. Wang, I. A. Yu, Phys Rev Lett 2006;96:043603.
8. X. Wang , D. Brown, K. Lindenberg, Phys Rev A 1988;37:3557-66.
9. Kh. I. Pushkarov, D. I. Pushkarov, and I. V. Tomov: Opt. Quant. Electr. 11(1979) 471.
10. J. M. Zhu and Z. Y. Ma: Chaos, Solitons & Fractals 33 (2007) 958.
11. S. Tanev and D. I. Pushkarov: Opt. Commun. 141 (1997) 322.
12. L. Gagnon: J. Opt. Soc. Am. A 6 (1989) 1477.
13. H. W. Schürmann: Phys. Rev. E 54 (1996) 4312.
14. Z. Birnbaum and B. A. Malomed: Physica D 237 (2008) 3252.
15. J. Fujioka and A. Espinosa: J. Phys. Soc. Jpn. 65 (1996) 2440.
16. S. L. Palacios: Chaos, Solitons & Fractals 19 (2004) 203.
17. A. Milgram, J. of Theoretical Biology, (2011), 271, 157-158.
18. J. Ghanouchi, H. Labiadh and K. Boubaker, Int. J. of Heat and Technology, 26 (2008), 49-53
19. S. Slama, J. Bessrour, K. Boubaker, M. Bouhafs, Eur. Phys. J. Ap. Ph. 44, (2008), 317-322
20. S. Slama, M. Bouhafs and K. B. Ben Mahmoud, Int. J. of Heat and Techn., 26(2), (2008),141-146.
21. S. Lazzez, K.B. Ben Mahmoud, S. Abroug, F. Saadallah, M. Amlouk, Current Applied Physics, 9 (5), (2009) 1129-1133
22. T. Ghrib, K. Boubaker and M. Bouhafs, Modern Physics Letters B, 22 (2008) 2893-2907
23. S. Fridjine, K.B. Ben Mahmoud, M. Amlouk, M. Bouhafs, Journal of Alloys and Compounds, 479 (2009) (1-2), 457-461
24. C. Khélia, K. Boubaker, T. Ben Nasrallah, M. Amlouk, S. Belgacem, Journal of Alloys and Compounds, 477(1-2) (2009) 461-467
25. K.B. Ben Mahmoud, M. Amlouk, Materials Letters, 2009, 63 (12), 991-994
26. M. Dada, O.B. Awojoyogbe, K. Boubaker, Current Applied Physics, Volume 9, Issue 3 (2009) 622-624.
27. S. Tabatabaei, T. Zhao, , O. Awojoyogbe, F. Moses, Int.J. Heat Mass Transfer, 45 (2009) 1247-1255.
28. A. Belhadj, J. Bessrour, M. Bouhafs, L. Barrallier, J. of Thermal Analysis and Calorimetry, 2009, 97, 911-920.
29. A. Belhadj, O. Onyango, N. Rozibaeva, J. Thermophys. Heat Transf. , 23 (2009) 639-642.
30. P. Barry, A. Hennessy, Journal of Integer Sequences, 13 (2010),1-34.
31. M. Agida, A. S. Kumar, El. Journal of Theoretical Physics, 7, (2010) 319-326.
32. A. Yildirim, S. T. Mohyud-Din, D. H. Zhang, Computers and Mathematics with Applications, 59 (2010) 2473-2477.
33. A. S. Kumar, Journal of the Franklin Institute, 2010, 347, 1755-1761.
34. S. Fridjine, M. Amlouk, Modern Phys. Lett. B, 23 (2009) 2179-2182
35. M. Benhaliliba, Benouis, C.E. Boubaker, K. Amlouk M. Amlouk, A. A New Guide To Thermally Optimized Doped Oxides Monolayer Spray-grown Solar Cells: The Amlouk-boubaker Optothermal Expansivity ψab in the book: Solar Cells - New Aspects and Solutions, Edited by: Leonid A. Kosyachenko, [ISBN 978-953-307-761-1, by InTech], (2011) 27-41.
36. H. Rahmanov, Studies in Nonlinear Sciences, 2 (1) (2011) 46-49.
37. N. Fabien II, M. Alidou, K. T. Crépin. Modulational instability in the cubic–quintic nonlinear Schrödinger equation through the variational approach. Optics Commun 2007;275(2):421-8.
38. V. E. Zakharov, E. A. Kuznetsov. Optical solitons and quasisolitons. Sov Phys JETP 1998;86:1035-46.
39. G. S. Agarwal and S. D. Gupta: Phys. Rev. A 38 (1988) 5678.
40. J. Fujioka and A. Espinosa: J. Phys. Soc. Jpn. 66 (1997) 2601.
41. C. Liu, Computer Physics Communications, 181, (2010) 317-324
42. S. Liang, D. J. Jeffrey, Computer Physics Communications, 180 ( 2009) 1429-1433
43. S. Liang, D. J. Jeffrey, Computer Physics Communications, 178 (2008) 700-712
44. T. Khang Nguyen, F. Rotermund, I. Park, A traveling-wave stripline dipole antenna on a substrate lens at terahertz frequency, Current Applied Physics, 14( 8) 2014, s 998-1004