Quantum Molecular Dynamics Simulation for Multifragmentation Resulting from an Expanding Nuclear Matter
A. Abdel-Hafiez*, M. E. Medhat
Department of Experimental Nuclear Physics, Nuclear Research Center, Atomic Energy Authority, Cairo, Egypt
Abstract
Quantum molecular dynamics (QMD) is used to investigate multifragmentation resulting from an expanding nuclear matter. Equation of state, the structure of nuclear matter and symmetric nuclear matter is discussed. Also, the dependence of the fragment mass distribution on the initial temperature (Tinit) and the radial flow velocity (h) is studied. When h is large, the distribution shows exponential shape, whereas for small h, it obeys exponentially falling distribution. The fragmentation mechanism in an expanding system is found to be different from the one in a thermally equilibrated system. The used Hamiltonian has a classical kinetic energy term and an effective potential term composed of four parts.
Keywords
Quantum Molecular Dynamics, Expanding Nuclear Matter, Multifragmentation, Fragment Mass Distribution
Received: February 26, 2015
Accepted: March 7, 2015
Published online: March 12, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
Multifragmentation has been a long-standing topic in nuclear physics. In particular, a fragment mass distribution has been extensively investigated both theoretically and experimentally as a phenomenon which might have some connection with nuclear phase transition1-6. Among the theoretical approaches, Fisher’s droplet model 7 is a familiar one which predicts the fragment mass distribution.
According to this model, the exponential falling distribution is derived under the condition that each fragment can be regarded as a thermally equilibrated droplet. This exponential falling distribution behavior has attracted many authors’ interest because the exponential falling distribution is a signature of a second order phase transition 8-13.
In order to investigate the relation between the fragmentation mechanism and the fragment mass distribution, many heavy ion collision experiments have been conducted 3–6. In these experiments, two types of fragment mass distribution have been observed. The exponential falling distribution is one of them and is originating from a spectator region where thermal equilibrium is often assumed 3,4. On the other hand, in a participant region, the source of fragments undergoes strong compression and each nucleon has large collective momentum at its decompression stage. Thus, we cannot regard this source of fragments as thermal equilibrated object that Fisher’s droplet model assumes. In this region, the mass distribution does not obey the power law but obeys an exponential distribution and the shape of which strongly depends on the collision energy 5,6.
There are several factors to prevent the direct understanding of fragmentation mechanism in heavy ion collision experiments. The finiteness of heavy ion collision is a source of complication. For instance, the surface effect during fragment formation might affect the distribution significantly. Moreover, it is doubtful whether thermal equilibrium is achieved even in a spectator region. To check the basic mechanism of fragmentation, therefore, it is desirable to adopt a model which does not assume a thermal equilibrium and is free from the complication arising from the finiteness of the system.
The analysis of nuclear matter is useful to avoid the complication coming from finiteness. Instability of nuclear matter against multifragmentation has been studied based on the Boltzmann-Langevin approach 14, classical molecular dynamics 11, kinetic equation 1, and linear response theory 15. These are simulations of an infinite system studying under what condition the instability against the multifragmentation occurs at high excitation. These studies, however, have not taken into account the collective expansion of the system explicitly. In 16, the effect of collective expansion have been treated in the framework of Boltzmann-Langevin approach and the fragmentation is discussed for a finite system. The instability to multifragmentation is also treated in the quantal RPA approach17.
The aim of this work is to investigate multifragmentation by using an expanding nuclear matter. When the matter expands slowly, it simulates a spectator region where each nucleon moves slowly. On the other hand, the rapid expansion simulates a participant region where the system has a rapid collective motion. The rate of expansion is controlled by only one parameter (h). By changing h we can investigate both spectator and participant regions. In the case of h=0, the system is just in a static thermal equilibrium state with temperature (T). Such a system is similar to what is assumed in Fisher’s droplet model. Our main purpose is to know how the fragment mass distribution depends on the expansion velocity and the temperature.
The used quantum molecular dynamics (QMD) and the nuclear matter at the saturation density r0 and a temperature Tinit .
On the basis of QMD, a series of simulations is carried out. There are four steps in the calculation.
1. The nuclear matter at the saturation density r0 and a temperature Tinit is prepared by Metropolis sampling method.
2. To this thermal matter with Tinit , a radial flow velocity (h) is imposed.
3. The time evolution of the system is calculated from r0 to 0.001 r0 by QMD.
4. A fragment mass distribution is calculated at 0.001 r0.
The Hamiltonian has a classical kinetic energy term and an effective potential term composed of four parts:
![]() (1)
(1)
![]()
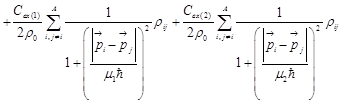 (2)
(2)
![]() (3)
(3)
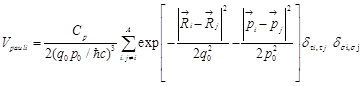 (4)
(4)
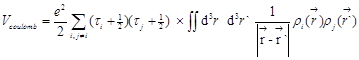 (5)
(5)
where si is the nucleon spin and ti is the isospin [ti =1/2 for protons and -1/2 for neutrons], áriñ is an overlap of one body density ri for ith nucleon with other nucleons defined as
![]() (6)
(6)
and the explicit form of ri is given by
![]() (7)
(7)
Where L is the squared width of the wave packet, L=1.95 fm2. This wave packet with fixed width is characteristic of the QMD model. It has the advantage of dealing with the many body correlation directly but imposes considerable restrictions on the instability of the nuclear matter.
We approximate the fermionic nature of the system by introducing the Pauli potential between two identical nucleons18,19, instead of antisymmetrization. The nuclear potential Vnucl has several components: The first two terms are Skyrme type nuclear interactions. The term with Cs0 is a symmetry potential where Ci is 1 for protons and 0 for neutrons. The last two terms with Cex(1) and Cex(2) are momentum dependent potentials originating from the exchange term of the Yukawa interaction. The term Vsurface stands for a surface interaction to describe the fragment property. The values of the parameters in the interaction are fitted to give good agreements with the nuclear matter saturation properties, the real part of optical potential, the rms radii of nuclei, and their binding energies.
The incompressibility constant K at the saturation point is simulated to the following parabolic form 20
![]()
Equation of state and the structure of nuclear matter
In this section we study properties of nuclear matter at several conditions. It is desirable to use a cell large enough to include several periods of structure and to avoid the spurious effects of the boundary condition on the structure of matter. Though our calculation with typically 1024 particles in a cell is not fully satisfactory in this respect, we consider it is enough for semi qualitative discussions at the beginning of this study. Actually, the global quantities, e.g., the ground state energy of the system, are well saturated at this number of particles in a cell.
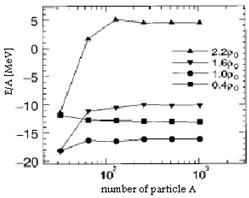
Fig. 1. Particle number dependence of the energy per nucleon of the infinite system for four average densities from r=0.4 r0 to 2.2 r0
In Fig. 1, we show the energy per nucleon of the infinite system as a function of the particle number in a cell for four average densities from r=0.4 r0 to 2.2 r0. For all densities, the energy of the system has already approached the asymptotic value above 256 particles within 100 keV/ nucleon. In this study we simulate an infinite system by the periodic boundary condition mainly with 1024 or 2048 particles in a cell, and investigate the ground state properties of nuclear matter.
Figure 2 shows the energy per nucleon as a function of the average density. The solid squares indicate the energy of ‘‘uniform’’ nuclear matter while open squares are the results of energy-minimum configurations.
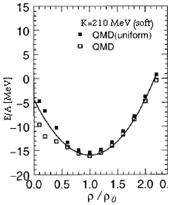
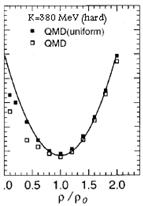
Fig. 2. The energy per nucleon of symmetric nuclear matter [Z/A=0.5] at zero temperature as a function of the average densities.
The ‘‘uniform’’ matter energy is calculated as follows: First we distribute nucleons randomly and cool the system only with the Pauli potential. The Pauli potential is repulsive and does not spoil the uniformity of the system. Then we impose the other effective interactions and cool only in the momentum space, fixing the positions of particles. The system turns out to be approximately uniform with this procedure. Note that simulated ‘‘uniform’’ matter is not exactly the same as ideal nuclear matter since the latter is continuous and completely uniform. Both cases of uniform and energy-minimum configurations have almost the same energy per nucleon for the higher densities as is seen in this figure. Below the saturation density r0, the energy per nucleon of the energy-minimum configuration is lower than the uniform case. The deviation amounts to about 5 MeV. As we see in the following, this is due to the structure change of matter from uniform to nonuniform such as a clusterized one21,22 .
From the left, the open squares are the results with soft [K=210 MeV] and hard EOS [K=380 MeV] obtained by the damping equation of motion searching the energy-minimum configuration in the full phase space. The solid squares indicate results obtained from the spatially uniform distribution. The kinetic energy of the electron is not included. We use 1024 particles in a cell for all cases.
If a system is finite and has high temperature and/or pressure, it expands spontaneously. However, an infinite matter cannot expand without an initial collective motion even if it has high temperature and pressure. Therefore, we give a collective momentum to each constituent nucleon so that the matter could expand homogeneously. This collective momentum is expressed in terms of one parameter h as
 (8)
(8)
where ![]() is the position of ith particle [the center of wave packet] measured from the center of the primitive cell and PF is the Fermi momentum at r0. The distance is normalized by using r0-1/3. The nearest neighbor pair of nucleons, on average, have a relative momentum hPF under this condition. Time evolution from r0 to 0.001 r0 by QMD
is the position of ith particle [the center of wave packet] measured from the center of the primitive cell and PF is the Fermi momentum at r0. The distance is normalized by using r0-1/3. The nearest neighbor pair of nucleons, on average, have a relative momentum hPF under this condition. Time evolution from r0 to 0.001 r0 by QMD
Table 1. Effective interaction parameter set
| K=210 MeV[soft] | K=380 MeV[hard] | |
| a [MeV] | -121.9 | -21.21 |
| b[MeV] | 197.3 | 97.93 |
| t | 1.33333 | 1.66667 |
| Cs0 [MeV] | 25.0 | 25.0 |
| Cex[1] [MeV] | -258.5 | -258.54 |
| Cex[2] [MeV] | 375.6 | 375.6 |
| m1 [MeV] | 2.35 | 2.35 |
| m2 [MeV] | 0.4 | 0.4 |
| VSF [MeV] | 20.68 | 20.68 |
| CP [MeV] | 115.0 | 115.0 |
| p0 [MeV] | 120.0 | 120.0 |
| q0 [fm] | 2.5 | 2.5 |
| L [fm2] | 1.95 | 2.05 |

Fig. 3. Snapshots of expanding nuclear matter at different densities. [a] An initial state with r=1.0 r0. [b] An intermediate state at r =0.05 r0 during the expansion. [c]
The time evolution of the nuclear matter with a given temperature Tinit and radial flow velocity with [h,Tinit] by QMD has been followed by Shinpei Chikazumi, et.al.23. Figure 3[a] shows a snapshot of an initial state at r=r0. Fig.3[b] shows a part of the whole system at r=0.05r0 during the expansion. The expansion is stopped when the average density reaches r=0.001r0 shown in Fig. 3[c]. In this procedure, the normal periodic boundary condition is not applicable to the expanding matter. Therefore, we introduce an extended periodic boundary condition.
2. Fragment Mass Distribution
The matter leave to expand until the average density becomes small enough so that each fragment can be identified. All the fragments are isolated when the average distance between nearest neighbor pair reaches about 5 fm at 0.05 r0. However, we noticed that the intrinsic expansion of fragments is not yet stopped at r=0.05r0 especially when h is large. Therefore, we set the final density equal to 0.001r0. At this density, all the fragments are stabilized so that we can identify them only by their positions.
We show our main result of the fragment mass distribution. The distribution strongly depends on the radial flow velocity h whereas the initial temperature has little effect on the distribution. First, we concentrate on the distribution for Tinit =30 MeV and investigate how the radial flow affects the distribution
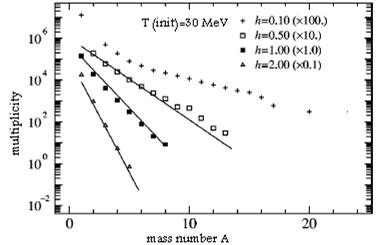
Fig. 4. The fragment mass distribution obtained in our QMD simulation in case of semi logarithmic scale.
Figure 4 shows the distributions calculated for h =0.1,0.5,1.0,2.0 with the initial temperature Tinit=30 MeV. In this figure, all the distributions follow straight lines except for h=0.1. These straight lines in the semi logarithmic scale mean that the number of large fragments decreases exponentially as fragment size increases. This exponential shape can be understood as the manifestation of random distribution24. When h is large enough to suppress the interaction, the final distribution is simply an enlarged copy of the initial configuration. Under this limit, the particles are randomly distributed irrespective of the interaction because the initial configuration is prepared at saturation density and the particles are randomly distributed under any temperature. The value of h directly corresponds to the radial flow velocity in the participant region. Actually, this kind of heavy ion collision is investigated by a simulation of a finite system with a radial flow velocity25. Figure 5 shows the same quantity as Fig. 4 in double-logarithmic scale. In our method, we can discuss most clearly the effect of radial flow because our system is an infinite expanding nuclear matter which is free from any finite size effect of the parent nucleus.
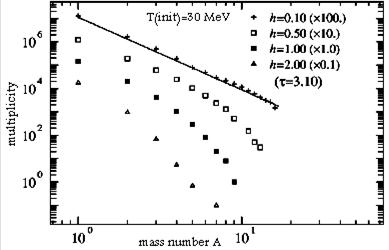
Fig. 5. The fragment mass distribution obtained in our QMD simulation in case of double logarithmic scale.
When h is small, the interaction must play an important role in fragmentation. In this case, h=0.1 follows a straight line whereas the others do not. The straight line in double-logarithmic scale refers to the so-called exponential falling distribution. The exponential falling distribution has been discussed in many works in connection with critical phenomena. Usually, exponential falling distribution is thought to be a manifestation that the system undergoes a second order phase transition. In the model assuming thermal equilibrium, the power law appears only when the second order phase transition happens. However, we must remember that the expanding system is completely in nonequilibrium.
Even when h=0.1, the system does not have enough time to reach thermal equilibrium where the temperature can be determined. Therefore this exponential falling distribution we obtained must be explained in a different way.
3. Expanding Fragmentation vs Isothermal Fragmentation
It is significant to compare two types of the exponential falling distribution, i.e., dynamical and isothermal ones. The isothermal fragmentation can be investigated by Metropolis sampling method. Like creating initial configuration, we prepare 1000 samples with a fixed temperature T at r=0.05 r0 instead of r=r0. From investigation of isothermal pressure, we have already known that the critical temperature is around 8 MeV. Fig. 6 shows how fragment mass distribution depends on the temperature T=5,8,18 MeV at r=0.05 r0. For T=5 MeV, the distribution shows the U-shape where large fragments and small fragments exist but there is no middle size fragments. T=8 MeV is just a critical temperature in which the exponential falling distribution appears. The exponent t, i.e., the slope of distribution, is around 2.5 which is consistent with the Fisher’s droplet model. As the temperature increases beyond the critical temperature Tc=8 MeV, the distribution deviates from the exponential falling distribution and becomes an exponential shape. In the bottom figure [T=18 MeV], thermal motion completely overcomes attractive interaction. Therefore, a random distribution appears like the rapid expansion case.
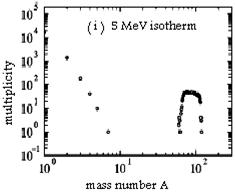
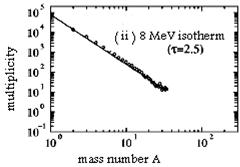
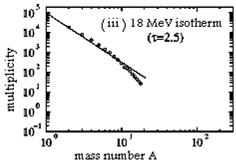
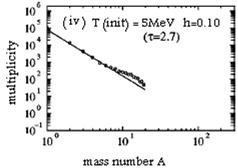
Fig. 6. The comparison between isothermal fragmentation and expanding fragmentation. The three figures [[i], [ii], and [iii]] are isothermal distributions [T=5,8 and 18 MeV] at r=0.05 r0. The two figures on the right hand side [ [iv] and [v] ] are the distributions obtained by the expansion [h=0.10].
4. Summary
In this paper we have presented the QMD approach for studying multifragmentation resulting from an expanding nuclear matter. We can reproduce well the finite nuclear properties for various mass ranges by inclusion of the Pauli and surface potential. We have investigated the EOS of nuclear matter by simulating an infinite system with the used QMD. The fragmentation during expansion can be classified according to the speed of expansion h. Also, the symmetric nuclear matter is discussed.
Our QMD model contains a further possibility for the simulation of the dynamical evolution of infinite nuclear matter such as supernova explosions, the glitch of the neutron star, and the initial stage of the universe. An intensive and systematic study of nuclear matter with the present model will be important since it contains fewer assumptions than the foregoing models as to the structure of matter.
References
- J. Schmelzer, G. Ro¨pke, and F.-P. Ludwig, Phys. Rev. C 55, 1917 [1997]
- A. Strachan and C. O. Dorso, Phys.Rev. C 59, 285 [1999]
- M. L. Gilkes et al., Phys.Rev. Lett. 73, 1590 [1994]
- P. F. Mastinu et al., Phys. Rev. Lett. 76, 2646 [1996]
- M. Petrovici et al., Phys.Rev. Lett. 74, 5001 [1995]
- W. Reisdorf et al., Nucl. Phys. A612, 494 [1997]
- M. E. Fisher, Rep. Prog. Phys. 30, 615 [1967]; in Critical Phenomena, Proceedings of the International School of Physics, Enrico Fermi Course LI, edited by M. S. Green [Academic, New York, 1971]
- I. N. Mishustin, Nucl. Phys. A630, 111c [1998]
- M. Belkacem, V. Latora, and A. Bonasera, Phys. Rev. C 52, 271 [1995]
- M. Colonna and Ph. Chomaz, Phys. Lett. B 436, 1 [1998]
- P. Finocchiaro, M. Belkacem, T. Kubo, V. Latora, and A. Bonasera, Nucl.Phys. A600, 236 [1996]
- A. Ohnishi and J. Randrup, Phys. Lett. B 394, 260 [1997]
- Y. Sugawa and H. Horiuchi, Phys. Rev. C 60, 064613 [1999]
- M. Colonna and Ph. Chomaz, Phys. Rev. C 49, 1908 [1994], and references therein
- V. Baran, M. Colonna, M. Di Toro, and A. B. Larionov, Nucl.Phys. A632, 287 [1998]
- A. Guarnera, M. Colonna, and Ph.Chomaz, Phys. Lett. B 373, 267 [1996]
- S. Ayik, M. Colonna, and Phys. Lett. B 353, 417 [1995]
- C. O. Dorso, S. Duarte, and J. Randrup, Phys. Lett. B 188, 287 [1987]
- T. Maruyama, K. Niita, K. Oyamatsu, T. Maruyama, S. Chiba, and A. Iwamoto, Phys. Rev. C 57, 655 [1998]
- Toshiki Maruyama, Koji Niita, Kazuhiro Oyamatsu, Tomoyuki Maruyama, Satoshi Chiba and Akira Iwamoto, Phys. Rev.C, Vol.57, No.2 [1998]
- S.Das Gupta, A.Z.Mekjian and B.Tsang, Advances in Nuclear Physics, V26, 89, 2001 ( J.Negele and E.Vogt, editors)
- C.B.Das, S.Das Gupta, W.Lynch, A.Z.Mekjian and B.Tsang, Phys. Reports, 406,1 (2005)
- Shinpei Chikazumi, Toshiki Maruyama, Satoshi Chiba, Koji Niita, and Akira Iwamoto, phys. Rev.C 63, 024602[2001]
- B. L. Holian and D. E. Grady, Phys. Rev. Lett. 60, 1355 [1988]
- W. Reisdorf et al., Nucl. Phys. A612, 494 [1997]



