Numerical Simulation of Free Liquid-Induced Vibrations in Elastic Shells
K. Degtyarev*, P. Glushich, V. Gnitko, E. Strelnikova
Strength and optimization department, A. N. Podgorny Institute for Mechanical Engineering Problems of the National Academy of Sciences of Ukraine, Kharkov, Ukraine
Abstract
The problem of dynamics analysis for shells of revolution partially filled with an ideal incompressible liquid was reduced to solving the system of singular integral equations. The direct formulation of boundary integral equation method was applied. The authors have elaborated the method of numerical simulation of the process and approved it by comparison of numerical and analytical solutions. They considered the shell vibrations coupled with liquid sloshing in presence of gravity forces. The free vibrations of elastic cylindrical shell were analyzed using the proposed technique.
Keywords
Fluid-Structure Interaction, Finite and Boundary Element Methods, Systems of Singular Integral Equations
Received: June 16, 2015
Accepted: July 4, 2015
Published online: July 22, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
Different engineering areas such as aerospace and chemical industry, power machine building, wind power engineering and transport extensively use thin-wall structural elements operated under excess process loads. In many circumstances these shells and shell structures are subjected not only to static loads but also to dynamic disturbances and filled with an internal fluid. The influences of both shell and fluid on each other must not be neglected in stress-strength analysis of these structural elements. So the interaction between the sloshing liquid and the shell structure has been the challenging field of research in many engineering applications. Fluid-structure interaction has been studied extensively in the last decade [1]-[3], etc.
Liquid sloshing is an interesting physical phenomenon of enormous practical interest that has far reaching applications in a wide field of technologies and engineering disciplines. It occurs in moving tanks with contained liquid masses such as rocket tanks, marine and space vehicles as well as in seismically excited storage tanks, dams, reactors, and nuclear vessels. The term "sloshing" means here the low frequency oscillation of free surface of liquid in a partially filled container. These oscillations can significantly influence the dynamic response of structures containing liquid. This interaction with sloshing liquid may lead to instabilities. Usually liquid storage tanks contain oil, flammable or toxic liquids. Destruction of these tanks by seismic action or shockwaves from a nearby explosion can lead to environmental catastrophe. So seismic design of liquid storage tanks requires knowledge of sloshing frequencies and hydrodynamic pressure on the walls [1]. Complex experimental investigation of loading processes is difficult and sometimes impossible for various reasons. Hence, mathematical modeling of physical processes with the help of advanced computer techniques is a basic approach for these problems. Numerical methods are especially useful when the geometry of container is complicated and the sloshing in the container cannot be investigated analytically. Various approaches have been proposed to research fluid-structure interaction, including the finite difference methods [4], the finite element methods (FEM) [3], the boundary element methods (BEM) [5-11]. The research findings are summarized in [12].
The dynamic analysis of shell structures is usually accomplished by usage of finite element programs. However, such 3D finite element analysis including the contained fluid is complex and extremely time consuming. In [8-10] authors offer the approach, based on the boundary element method, to the problem of free vibrations of fluid-filled shell of revolution as well as to the problem of liquid sloshing in rigid tank.
In this paper, analysis of elastic cylindrical shell vibration coupled with liquid sloshing is carried out. For this, here we use combination of reduced finite and boundary element methods. The analysis consists of several stages, and each represents a separate task. The frequencies and modes of empty shell vibrations are defined in the first stage. Displacement vector that is the solution of the hydrodynamic problem is sought as a linear combination of natural modes of empty shell. First, we define the frequencies and free vibration modes of fluid-filled elastic shell neglecting the force of gravity. Then we obtain the same, this time involving gravity, but assuming the shell rigid. Two latter problems are solved using reduced BEM. Then we come to the problem of coupled analysis of liquid sloshing and structural vibrations.
2. Problem Statement
Let us consider the coupled problem for the shell of revolution interacting with a liquid (Figure 1). We denote the wetted part of the shell surface by S1 and the free surface of a liquid by S0. Let us suppose that the shell geometry is defined in global Cartesian coordinate system x,y,z and free surface lies in xOy plane in the state of rest.
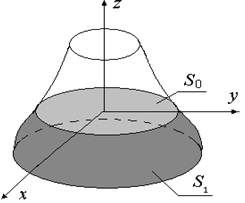
Fig. 1. Shell of revolution partially filled with a liquid.
The main objective of this paper is to find out and evaluate modes and frequencies of elastic shell of revolution free vibrations coupled with liquid sloshing.
In this study, liquid contained in the shell is assumed inviscid and incompressible one and its flow induced by vibrations of the shell is assumed irrotational.
Under these suppositions, there exists a velocity potential Φ defined as
This potential satisfies the Laplace equation.
The equations of motion of the two media (the shell,![]() , and the fluid with free surface,
, and the fluid with free surface, ![]() , (see Fig. 1)) can be written in the following form
, (see Fig. 1)) can be written in the following form
![]() (1)
(1)
where U is the vector-function of displacements, P is the fluid pressure on a moistened surface of the shell, and L and M are the operators of elastic and mass forces.
Let us consider the right-hand side of Eqn. (1). It should be noted that the vector P is normal to the considered shell, what is the feature of the ideal fluid. We will denote ![]() . Assuming that the natural velocity of the fluid is zero, the value
. Assuming that the natural velocity of the fluid is zero, the value ![]() , according to the Cauchy-Lagrange integral, can be represented as follows
, according to the Cauchy-Lagrange integral, can be represented as follows
![]()
where Φ is the velocity potential, g is the free fall gravity acceleration, z is the vertical coordinate of a point in liquid, ![]() is the atmospheric pressure and
is the atmospheric pressure and ![]() is the fluid density.
is the fluid density.
To obtain the boundary equations over the free surface we have formulated dynamic and kinematics boundary conditions. The dynamic boundary condition consists in equality of liquid pressure at its free surface to atmospheric one. The kinematics boundary condition requires that particles of liquid free surface remain there all the time of subsequent motion. So, we have
![]() ,
,
where an unknown function ![]() describes the form and location of free surface.
describes the form and location of free surface.
Thus, to find the velocity potential Φ, we obtain the following boundary value problem:
![]() ,
, ![]() ,
, ![]() .
.
Here ![]() is for normal component of shell deflection, n is for external unit vector normal to the shell wetted surface.
is for normal component of shell deflection, n is for external unit vector normal to the shell wetted surface.
So we reduce the problem under consideration to the following system of differential equations:
![]() ;
; ![]() ;
; ![]()
with the next set of boundary conditions relative to Φ
![]() ,
, ![]()
![]()
and shell fixation conditions relative to U.
To define coupled modes of harmonic vibrations we represent the vector U in the form U=u exp(iwt) , where w is an own frequency and u is a mode of vibration of the considered shell containing some fluid.
3. The Mode Superposition Method for Coupled Dynamic Problems
We will seek vibration modes for shell with liquid in the form
![]() (2)
(2)
where ![]() are unknown coefficients and
are unknown coefficients and ![]() are the normal modes of vibrations of the empty shell. In other words, a mode of vibration of the shell filled with fluid is determined as a linear combination of normal modes of its vibration without liquid.
are the normal modes of vibrations of the empty shell. In other words, a mode of vibration of the shell filled with fluid is determined as a linear combination of normal modes of its vibration without liquid.
Let us note that the following relations are valid
![]() (3)
(3)
Hence
![]() (4)
(4)
where ![]() is the
is the ![]() -th frequency of empty shell vibrations. The above relations (3) and (4) show that the modes of shell vibrations
-th frequency of empty shell vibrations. The above relations (3) and (4) show that the modes of shell vibrations ![]() are orthonormalized with respect to the mass matrix.
are orthonormalized with respect to the mass matrix.
We will seek Φ as a sum of two potentials ![]() as it was proposed in [9].
as it was proposed in [9].
Let us represent the potential Φ1 as the following series expansion
![]() (5)
(5)
Here time-dependant coefficients ![]() are the same as in Eqn. (2).
are the same as in Eqn. (2).
To determine j1k we have the following boundary value problems:
![]() ,
,![]() ,
, ![]() (6)
(6)
It would be noted that the solution of boundary value problem (6) was done in [10].
To determine the potential F2 we have to solve the problem of fluid vibrations in rigid vessel taking into account gravitational force. It leads to following representation of potential F2:
![]() (7)
(7)
where functions j2k are natural modes of liquid sloshing in the rigid tank. To obtain these modes we have solved the following sequence of boundary value problems:
![]() ;
; ![]() (8)
(8)
![]() (9)
(9)
We have differentiated with respect to t the second of equations (9) and substituted there ![]() by the left-hand side from the first one. Let us suppose hereinafter that
by the left-hand side from the first one. Let us suppose hereinafter that ![]() . Then we obtain for each j2k the sequence of eigenvalue problems with following conditions over the free surface:
. Then we obtain for each j2k the sequence of eigenvalue problems with following conditions over the free surface:
![]() . (10)
. (10)
The effective numerical procedure for solution of these eigenvalue problems using boundary element method was introduced in [7].
Finally, we obtain the following expression for potential F:
![]() (11)
(11)
It follows from Eqn. (11) that function ![]() can be written as
can be written as
![]() (12)
(12)
So, the total potential F satisfies the Laplace equation and non penetration boundary condition
![]() ;
; ![]()
due to validity of relations (6),(8). Noted that F also satisfies the condition
![]()
as a result of representation (12).
Satisfying the condition
![]()
over the free surface, one can obtain the next equality
![]() (13)
(13)
When functions j1k and j2k are found, we substitute them in Eqn (1) by corresponding expressions and obtain the following relations
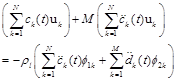 (14)
(14)
![]() .
.
Here we have simplified Eqn (13) taking into account Eqns (6),(10).
The first equation in (14) is valid over the wetted surface of the shell and the second one – over the free surface of liquid.
Considering the result of dot product of first equation in (14) by uj and second one by ![]() , and taking into account relations (3),(4) and orthogonality of natural modes of fluid vibrations in rigid vessel, we come to the fpllowing set of n+m second order differential equations, which determine unknown coefficients
, and taking into account relations (3),(4) and orthogonality of natural modes of fluid vibrations in rigid vessel, we come to the fpllowing set of n+m second order differential equations, which determine unknown coefficients ![]() :
:
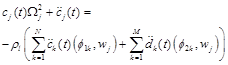 (15)
(15)
![]()
So, to solve coupled problem of elastic shell of revolution free vibrations with liquid sloshing inside it is necessary to obtain three systems of basic functions: natural modes of empty shell; modes of fluid-filled elastic shell without force of gravity; and modes of liquid in rigid shell under force of gravity.
To find coupled modes of harmonic vibrations we represent the time-dependant unknown coefficients as
![]() (16)
(16)
where w is the natural frequency, and ![]() are unknown constants.
are unknown constants.
Taking into account Eqns (16), one can express the Eqns (15) as
 (17)
(17)
![]()
Introducing the following matrixes and vectors
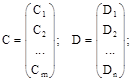
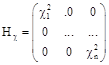
 ;
;
![]() ;
;
![]() ;
; ![]() ,
,
we come to the following problem:
![]() ;
;
![]() .
.
Let also introduce for simplicity vectors and matrix of dimension ![]()
![]() ;
; ![]() ;
;![]()
It brings us to the following eigenvalue problem
![]() (18)
(18)
So, analysis of elastic shell free vibrations coupled with liquid sloshing is reduced to solution of eigenvalue problem (18). It should be emphasized that hereinbefore we did not assume that our shell must be a shell of revolution.
Hereinafter we will use finite element method to find basic functions wj, and boundary element method to find basic functions j1k , j2k.
The proposed technique allows us to carry out numerical simulation for different value of gravitational acceleration g.
4. Systems of the Boundary Integral Equations and Some Remarks About Their Numerical Implementation
Now and hereinafter we consider the shells of revolution only.
The basic procedure is to start with the standard boundary integral equation for surface potential [5], replace the Cartesian co-ordinates (x, y, z) with cylindrical co-ordinates (r, q, z), and integrate with respect to z and q.
We use furthermore the cylindrical coordinate system and represent unknown functions as Fourier series by circumferential coordinate
![]() (19)
(19)
where a is a given integer (the number of nodal diameters).
We will seek both harmonic functions j1k and j2k as the sums of potentials of single and double layers [6], i.e., we will use the direct boundary element method formulation. Hereinafter we will drop indexes ij for simplicity. So we have
![]() (20)
(20)
It is assumed here that S = S1 È S0 and the points P and P0 belong to the surface S. The value êP – P0 ê represents the Cartesian distance between the points P and P0.
For the mixed boundary value problem defined by Eqs. (6), the representation (20) leads to the following system of the singular integral equations for unknown functions j and q:
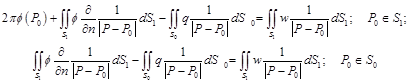 (21)
(21)
In this system, function j defined over the surface S1 represents the pressure on the moistened shell surface, and the function q defined over the free surface of liquid S0 is the velocity normal component of this surface particles.
Let G be a generator of the surface S1. It has been proved in [7,9] that system (21) can be written in the form
![]() (22)
(22)
![]()
Here
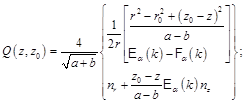
![]()
![]() ;
;
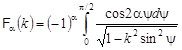 ;
;![]()
![]() .
.
To find potentials j2k we use representation (20) and introduce the next integral operators:
![]() ;
; ![]()
![]() ;
;
![]() ;
; ![]() (23)
(23)
Then the boundary value problem (8),(10) takes the form
![]() ;
; ![]() ;
;![]() ;
; ![]() .
.
After excluding function y1 from these relations, we obtain the following eigenvalue problem, solution of which gives natural modes and their frequencies for liquid sloshing in rigid tank
![]() .
.
Numerical solution of integral equation system (22) and evaluation of integral operators (23) is obtained by BEM with constant approximation of unknown j and q inside elements.
It would be noted that internal integrals in (22),(23) are complete elliptic integrals of first and second kinds. As the first-kind elliptic integrals are non-singular, one can successfully use standard Gaussian quadratures for their numerical evaluation. For second-kind elliptic integrals we have applied the approach based on characteristic property of the arithmetic geometric mean AGM(a,b) (see [13]). This property is the following:
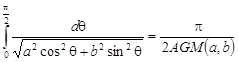 .
.
To find AGM(a,b) there exist the simple Gaussian algorithm, described below
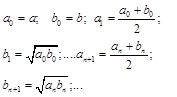
![]() (24)
(24)
It is a very effective method to evaluate the elliptic integrals of the second kind. Convergence ![]() is achieved after 6 iterations (namely, n=6 in (24)).
is achieved after 6 iterations (namely, n=6 in (24)).
So we have the effective numerical procedures of inner integrals evaluation, but integral equations (22), (23) involve external integrals of logarithmic singularity and thus numerical treatment methods for these integrals must also take into account the presence of this integrable singularity. Here integrands have strongly nonuniform distribution over the element, and standard integration quadratures show low accuracy. So we treat these integrals numerically by special Gauss quadratures [6,14] and applying technique proposed in [15].
5. Some Numerical Results
The study of axisymmetric free vibration characteristics of elastic cylindrical shell interacting with a liquid is presented below. In this special case, parameter a in Eqns (19), (22), (23) is supposed equal to zero.
Let our shell be the circular cylindrical tank with flat bottom. Its geometry is shown in Figure 2. The shell has the following characteristics: the radius R = 1 m, thickness h = 0.01 m, the length L = 2 m, Young’s modulus E = 2·105 MPa, Poisson’s ratio ν = 0.3, density of material r = 7800 kg/m3, the fluid density rl = 1000 kg/m3. The filling level of the fluid is denoted as H. The shell is assumed pin-connected over its contour and boundary conditions are following: ![]() to z = 0 and r = R.
to z = 0 and r = R.
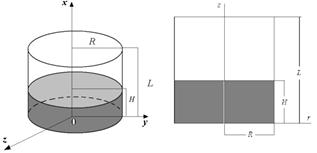
Fig. 2. Cylindrical shell partially filled with a liquid.
The three systems of basic functions mentioned in section 3 above have been built.
The first one - normal modes of the empty shell vibrations - was obtained using finite element method (FEM) as it was described in [9].
The second system represents normal modes of liquid sloshing in the rigid tank with taken into consideration gravity force. To verify the proposed numerical algorithm described further, we have used the analytical solution [11] that can be expressed in the form
![]()
![]() (25)
(25)
The values ![]() in (25) are the roots of the first kind Bessel function
in (25) are the roots of the first kind Bessel function ![]() derivative,
derivative, ![]() are our sought-after frequencies and modes of liquid sloshing in the rigid cylindrical shell.
are our sought-after frequencies and modes of liquid sloshing in the rigid cylindrical shell.
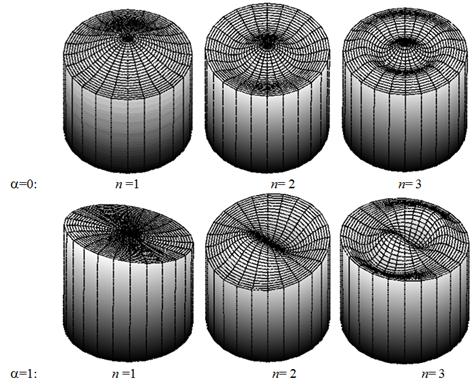
Fig. 3. Modes of liquid sloshing in the rigid cylindrical shell.
The numerical solution was obtained by using BEM as it was described beforehand. Some numerical results were also provided in [15]. In present numerical simulation we used 60 boundary elements along bottom, 60 elements along wetted cylindrical part and 100 elements along the radius of free surface. Figure 3 shows the first three modes of liquid sloshing on free surface in the rigid cylindrical shell.
Table 1 below provides the numerical values of the natural frequencies of liquid sloshing for nodal diameter a =0. The obtained numerical results are compared with those received using formulae (25).
Table 1. Comparison of analytical and numerical results.
| n=1 | n=2 | n=3 | n=4 | n=5 | ||
| a=0 | BEM | 3.815 | 7.019 | 10.180 | 13.333 | 16.480 |
| (23) | 3.815 | 7.016 | 10.173 | 13.324 | 16.470 | |
| a=1 | BEM | 1.657 | 5.332 | 8.540 | 11.711 | 14.889 |
| (23) | 1.657 | 5.329 | 8.536 | 11.706 | 14.863 | |
Figures 4 and 5 also demonstrate good agreement between numerical and analytical data.
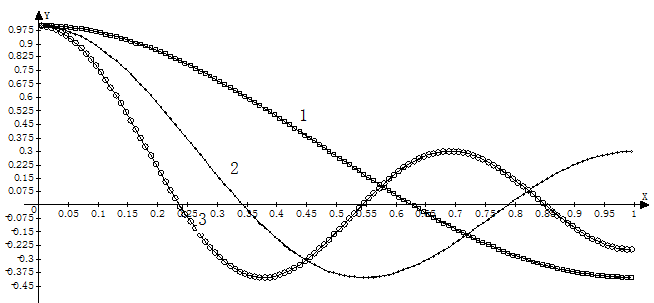
Fig. 4. Numerically and analytically obtained modes
In Figure 4 the distribution of first three sloshing modes over the free surface is shown. The solid lines correspond to modes obtained with the help of analytical expression (25) at z = H.
Figure 5 demonstrates the distribution of these modes over the rigid vertical wall of the shell.
The lines plotted with circles and squares correspond to numerical solutions. Numbers 1,2,3 mark the first, second and third mode of liquid sloshing, respectively. Accuracy ε of order 10-4have been achieved in numerical data calculation.
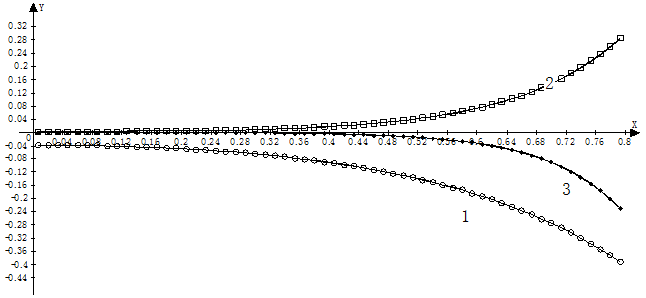
Fig. 5. Sloshing modes on the vertical wall
Functions j1k were calculated by BEM based method developed in [9].
Table 2 provides the numerical values of natural frequencies of vibration for empty and for fluid-filled cylindrical tanks. Here coefficients nS, nL indicate number of shell modes and quantity of liquid involved in coupled vibrations, n is the number of coupled mode. For numerical simulation represented here, we have used 4 shell modes and 5 sloshing modes.
Table 2. Frequencies of empty and fluid-filled tanks.
| a =0 | a =1 | |||||||
| n | nS | nL | Empty elastic tank | Fluid-filled tank | nS | nL | Empty elastic tank | Fluid-filled tank |
| 1 | 1 | 6.11932 | 1 | 4.03300 | ||||
| 2 | 1 | 1,2 | 23.233 | 7.94464 | 2 | 7.2328 | ||
| 3 | 2 | 8.29916 | 3 | 9.15547 | ||||
| 4 | 3 | 9.99588 | 4 | 10.7233 | ||||
| 5 | 4 | 11.4410 | 5 | 12.0857 | ||||
| 6 | 5 | 12.7239 | 1,2 | 48.5207 | 21.9555 | |||
| 7 | 2,1 | 91.1011 | 43.8628 | 2,1 | 139.708 | 79.7191 | ||
| 8 | 3,2 | 205.252 | 119.627 | 3,2,1 | 232.443 | 178.422 | ||
| 9 | 4,3,2 | 365.795 | 238.695 | 4,3 | 277.303 | 210.007 | ||
The numerical analysis demonstrates that the lowest frequency corresponds to liquid sloshing at a = 1. The frequencies of the fluid-filled shell are essentially lower than those of the empty shell. It also would be noted that there exist an interaction between both liquid and wall vibrations. It was observed for the first shell mode. This does not allow us to consider separately the spectra of frequencies of the shell and liquid sloshing.

Fig. 6. Conical shell partially filled with a liquid.
The next problem is concern with liquid sloshing in the conical tank (figure 6) Analytical solution of this problem was based on the formulas obtained in [14]. Numerical solution was done by the method described above
To solve the problem a grid of n boundary elements on the shell meridian and m boundary elements on the free surface of the liquid was created. Table. 3 contains the calculation results for the first two eigenvalues ![]() when
when ![]() , b= R/2 for a= 0 and a = 1 depending on the parameters n and m.
, b= R/2 for a= 0 and a = 1 depending on the parameters n and m.
Table 3. Split-depended convergence of eigenvalues.
| n+ m | a=0 | a=1 | ||
| 1 | 2 | 1 | 2 | |
| 10+10 | 3.54 | 6.93 | 1.39 | 5.15 |
| 20+20 | 3.50 | 6.78 | 1.38 | 5.05 |
| 30+30 | 3.48 | 6.74 | 1.37 | 5.02 |
| 40+40 | 3.47 | 6.71 | 1.37 | 5.01 |
| 3.46 | 6.70 | 1.36 | 4.97 | |
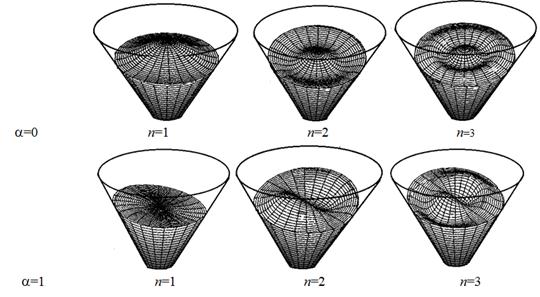
Fig. 7. Natural modes of liquid sloshing in conical shell.
Figure 7 shows up free surface eigenmodes of sloshing liquid in conical shell for two lowest frequency parameters. The good agreement and convergence of results in both examples demonstrate the reliability of the received data, the efficiency of the method and algorithm for solving the problem.
6. Conclusions
The shell vibrations coupled with liquid sloshing under force of gravity were considered. The free vibration analysis of the elastic cylindrical shell was carried out using proposed techniques. We introduce the representation of the velocity potential as the sum of two potential, one of them corresponds to problem of the fluid free vibrations in the rigid shell and another one corresponds to problem of fluid-filled elastic shell vibrations without including the gravitational component. The spectrum of frequencies for cylindrical tank was analyzed.
The main conclusion is following. Vibrations consist of two components: one of which is produced by liquid sloshing, but another caused by elastic shell vibrations. Hence these components are both essential. It means that we do not have to consider these components separately. Thus instead two separate problems one general problem has to be considered.
Acknowledgments
The authors gratefully Carlos Brebbia, Wessex Institute of Technology, United Kingdom, for his constant support and interest to our research.
References
- G. Popov, S. Sankar, T.S. Sankar, G.H. Vatisin, Liquid Sloshing in Rectangular Road Container. Computers & Fluids. V.21, N 4, pp.551-569. 1999.
- Kumar,V. &Ganesan,N.,Dynamic analysis of conical shells conveying fluid. Journal of Sound and Vibration, 310(1-2), pp.38–57,2008.
- Tezduyar T. E. Finite Element Methods for Fluid Dynamics with Moving Boundaries and Interfaces. Encyclopedia of Computational Mechanics, (3): Fluids, pp.1-55, 2004.
- Dukowicz, J. K., Dvinsky, and A. S., Approximate Factorization as a High Order Splitting for the Implicit Incompressible Flow Equations, J. Comput. Phys., 102 , pp. 330-336, 1992.
- Recent Advances in Boundary Element Methods A Volume to Honor Professor Dimitri Beskos Manolis, George; Polyzos, Demosthenes Eds., XXXVIII, 470 p., 2009.
- Brebbia, C.A., Telles, J.C.F. & Wrobel, L.C. Boundary Element Techniques, Springer-Verlag: Berlin and New York, 1984.
- J. Cappello, A. Sauret, F. Boulogne, E. Dressaire, H. Stone, Damping of liquid sloshing by foams: from everyday observations to liquid transport, Journal of Visualization, pp. 1-3, 2014.
- Strelnikova E., Yeseleva E., Gnitko V., Naumenko V. Free and forced vibrations of the shells of revolution interacting with the liquid Proc. of XXXII Conference "Boundary elements and other mesh reduction methods" WITPress, Transaction on Modeling and Simulation, pp. 203-211, 2010.
- Ventsel E.,. Naumenko V, Strelnikova E., Yeseleva E. Free vibrations of shells of revolution filled with a fluid. Engineering analysis with boundary elements, 34, pp. 856-862, 2010.
- Gnitko V., Marchenko U., Naumenko V., Strelnikova E. Forced vibrations of tanks partially filled with the liquid under seismic load. Proc. of XXXIII Conference "Boundary elements and other mesh reduction methods" WITPress, Transaction on Modeling and Simulation, pp. 285-296, 2011.
- Chen, Y.H., Hwang, W.S. & Ko, C.H., Numerical simulation of the three-dimensional sloshing problem by boundary element method. Journal of the Chinese Institute of Engineers, 23(3), pp. 321-330, 2000.
- Ibrahim R. A. Liquid sloshing dynamics: theory and applications Cambridge University Press, 957p., 2005.
- David A. Cox. The Arithmetic-Geometric Mean of Gauss. L’Enseignement Mathemaique, t. 30, pp. 275 -330, 1984.
- Stroud A.H., Secrest D. Gaussian Quadrature Formulas. Prentice-Hall, Englewood, N.J., Cliffs, 206 p., 1966.
- Naumenko V.V., Strelnikova H.A. Singular integral accuracy of calculations in two-dimensional problems using boundary element methods. Engineering analysis with boundary elements. №26, pp. 95-98, 2002.



