Diamagnetism of Longitudinal Autosoliton in p-InSb in Longitudinal Magnetic Field

I. K. Kamilov, A. A. Stepurenko^*, A. E. Gummetov

Dagestan Institute of Physics after Amirkhanov, Dagestan Scientific Center of the Russian Academy of Sciences, Makhachkala, Russia

Abstract

A longitudinal thermal-diffusion autosoliton generated in the non-equilibrium electron-hole plasma in p-InSb is shown to be diamagnetic in an external longitudinal magnetic field. The phenomenological estimate of the question allows deriving an expression for the magnetization, magnetic induction, and diamagnetic susceptibility of the autosoliton under an external magnetic field. Plots for these expressions, and computations and numerical estimations of the diamagnetism are performed.

Keywords

Autosoliton, Semiconductors, Non-Equilibrium, Dissipative Structure, Oscillations, Electron-Hole Plasma, Diamagnetism, Magnetic Field

Received: June 2, 2015
Accepted: June 13, 2015
Published online: July 23, 2015

@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/

1. Introduction

It is known [1] that all materials are magnetic. Their huge variety occurs in nature. A main contribution into the magnetism is made by electrons revealing intrinsic resultant magnetic moments – spin, orbital. In an external magnetic field, spin magnetic moments are oriented in the direction of the field generating a paramagnetic magnetization, while orbital magnetic moments are directed against the field creating a diamagnetic magnetization. As for InSb, it can be referred to weakly magnetic materials.

Cr-compensated InSb-samples with carrier concentrations of p ~ 10¹² cm³ measured under a strong electric field [2,3] exhibit a consistently high conductance triggered by autosolitons (AS) formed in a non-equilibrium and excited electron-hole plasma (EHP) generated by the joule heat­ing in the electric field. AS is a steady isolated intrinsic stable state of a system, in our case, of non-equilibrium carriers in semiconductors and semiconducting structures. In other words, AS is localized areas of extreme carriers concentrations and their temperatures. The EHP generated by the impact ionization, injection or traveling Gunn domain in GaAs thin films stratifies for current filaments and domains of electric field [4,5,6,7]; longitudinal ASs are found in n-Ge in EHP photogenerated, warmed by the electric field [8]; space-time structures in the form of static and pulsing current filaments in p-i-n diodes are studied in works [9,10]. The longitudinal autosoliton – the current filament implemented in p-InSb – we are interested in is a microlocalized region of enhanced carriers concentration and lower temperature (a cold AS) [11]. The estimation of autosoliton carriers concentration n_AS in studied samples gives a value of n_AS~10¹⁸ cm^-3, while the initial specific carriers concentration in the sample is n = 10¹² cm^-3. Facts pointed out allow to consider that the conductivity and all electrical physical properties of the sample may be substituted by AS and its behavior under an external influence.

2. Review Experimental Results

Due to the fact that in the cold AS [11], the carrier concentration is higher in the center than in the periphery, a diffusional outflow from AS center to the periphery happens. Since the electron mobility considerably exceeds the hole mobility µ_е ≈ 100µ_р [12] the diffusional flow of electrons from AS center to the periphery will occur and a region along an AS central axis will be hole-rich. In an external longitudinal magnetic field, the electrons of this flow will start to rotate in spiral around the hole-enriched central area and simultaneously the electrons are involved in an ambipolar drift together with holes in the electric field applied to the sample.

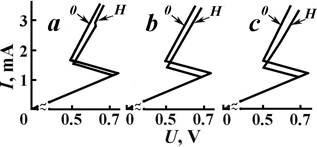
Fig. 1. Dynamic voltage-current characteristics of p-InSb at constant values of the applied longitudinal magnetic field: a – H1 = 2.4 104 A/m, b – H2 = 3.7 ·104 A/m, с – H3 = 6.2 104 A/m.

If we regard each turn of the spiral as an electron orbit around the positively charged center we could liken the indicated orbit to the electron orbit in atom. All orbits in AS in the longitudinal magnetic field are parallel to each other; lie in a plane perpendicular to the current and mag­netic field directions. Possessing the orbital magnetic moment the turns define a total magnetic moment of the AS M_AS. Summing up, we can conclude that the longitudinal AS becomes a diamagnet in the external longitudinal magnetic field. The experimental investigations on a behavior of AS current in Cr-compensated p-InSb under the longitudinal magnetic field show the voltage-current characteristics exhibiting the formation of AS and a change in the current with increase in the electric field to be different from the voltage-current characteristics (VCC) obtained at the external longitudinal magnetic field (Fig. 1). The AS current change in the magnetic field occurs at lower values than in the absence of that. When increasing the magnetic field, the difference of the current change on VCC rises. As is evident from Fig.1, a change in the sample conductivity in the longitudinal magnetic field does not occur in the ohmic region, i.e. when the AS lacks. In the case of AS presence (the non-linear region of VCC), the change of the sample conductivity or the AS current under the longitudinal magnetic field is associated with a change either in AS carriers concentration or in carriers mobility. A decrease in the longitudinal current with the increase of the longitudinal magnetic field is caused, on the one hand, by a fall in the mobility because of the path curvature of radially moving electrons, on the other hand, by a de­crease in the mobility in accordance with µ ~ 1/n for a densifying initial plasma as a result of the current filament compression in the longitudinal magnetic field. And the carrier concentration in AS remains unaltered, but the specific concentration of carriers in AS changes due to the variation of an AS transversal size.

Work [13] reported that the longitudinal AS implemented in p-InSb can move in the Lorentz force direction at application of transversal magnetic field to the sample. Works [14,15] reported that the longitudinal AS formed in the non-equilibrium EHP in p-InSb moves in the direction of the sample periphery under the influence of the transversal magnetic field. On the other hand, it is experimentally shown [16] that the flow of the current filament in samples realized in the transversal magnetic field with a simultaneous effect of the longitudinal magnetic field fails. Put it in other words, the galvanomagnetic Ettingshausen effect appeared in the longitudinal AS in the longitudinal magnetic field inducing a AS flow in the sample is entirely blocked by the diamagnetism occurred in AS in the external longitudinal magnetic field.

Fig. 2. Gauss-ampere characteristics for different currents of the longitudinal AS under the transversal magnetic field in the absence and presence of the longitudinal magnetic field _|| = 7.2 10⁴ A/m = const.

Fig. 2 exhibits dependences of three different currents of the longitudinal AS on the transversal magnetic field H_⊥ (Gauss ampere characteristics – GAC) with the longitudinal mag­netic field (straight lines) and without that (curve lines).

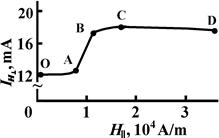
Fig. 3. Dependence of the longitudinal AS current under transversal magnetic field I_H⊥ on the longitudinal magnetic field Н_||.

As is evident from Fig. 2, the longitudinal AS current in the transversal magnetic field does not vary at a simultaneous effect of the constant longitudinal magnetic field. In the absence of the longitudinal magnetic field, the influence of the transversal magnetic field on the longitudinal AS current is essential [14,16].

Fig. 3 demonstrates the dependence of AS current in the specified transversal magnetic field I_H⊥ (H_⊥ = const) with a change in a longitudinal magnetic field value GAC. As is evident from Fig. 3, when increasing the longitudinal magnetic field the I_H⊥ smoothly rises (OA segment) first and then abruptly jumps (AB segment) with a following transition for saturation or even decreasing (CD segment). The OA segment indicates a linear slowing-down in the AS flow in the transversal magnetic field. The AB segment – the abrupt positive jump of the current – testifies to a sharp slowing-down and a failure of the current filament flow. The BD segment shows a change in the AS current to be occurred only under the longitudinal magnetic field though the transversal magnetic field presents.

The observed effect is implemented due to simultaneous realization of two phenomena considered in works [13,14,17]. As works [13,14] depict, the current filament gains a temperature gradient in the Lorentz force direction under the influence of the transversal magnetic field by reason of the Ettingshausen effect. It is this temperature gradient that provides the transfer of the AS in the direction of the sample periphery characterized by a low temperature. In the dependence of transversal dimensions of the sample the AS achieves a sample boundary or such a temperature region where the longitudinal AS vanishes. It is experimentally observed a sharp decrease in the current or the instability of the longitudinal AS. On the other hand, in the longitudinal magnetic field, the longitudinal AS becomes a diamagnet, i.e. it is a cylinder consisting of electron path spirals moving around the hole-enriched region generating a self-magnetic field [17]. Spinning electrons are able to the heat transport from a hot current filament to a cold one. The higher the longitudinal magnetic field is, the faster the electrons spin, and the greater the heat transport is. Consequently, the temperature gradient difference of current filament fronts provided the flow of current is smoothed, what causes the slowing of the filament. The temperature gradient in the current filament disappears at a certain sufficient value of the longitudinal magnetic field and, consequently, the current filament fails to drift though the same transversal magnetic field presents. So, the Ettingshausen effect is blocked by the longitudinal magnetic field.

3. Phenomenological Consider, Results and Discussion

It can be suggested the longitudinal AS will change into the diamagnet in the longitudinal magnetic field of a minimum value H₀ when the cyclotron radius r of electron spinning diffusing in the transversal direction with respect to the hole-rich region will be equal to an electron diffusion length L_e, i.e. r = L_e = m_eυ_d µ₀eH₀, υ_d = 2πL_e  τ_е. We obtain τ_е = 2πm_e µ₀eH₀, f = µ₀eH₀ 2πm_e, where υ_d is the electron diffusive drift rate, τ_е is the time of electron one turn in an orbit or the electron lifetime, f is the rate of electron orbital rotation, µ₀ is the magnetic permeability of the vacuum. When a value of the longitudinal magnetic field is H₀ = 2πm_e µ₀eτ_е, the longitudinal AS is a cylinder consisting of electron path spirals spinning around the hole-enriched region generating a self-magnetic field. Fig. 4 presents the oscillograms of dependences differing by initial values of AS currents from the longitudinal magnetic field applied to the sample as triangular impulse – the dynamic GAC. The determination of a minimum magnetic field H₀ at which the AS is changed into the diamagnet is the goal of the creation of such GAC. Measurements made using this and other methods provide the value of the magnetic field H₀ ≈ 2000 A/m. We obtain the value of AS electron lifetime t = 2πm_e µ₀eH₀ from known expression for τ_е= 4.3 ∙ 10^-10 s. This value is close to the results obtained in [12]. Let`s consider each spiral turn as the orbit of electron motion in the atom. All orbits are mutually parallel and perpendicular to the direction of the external magnetic field. Possessing the magnetic moment M_е the turns define the total magnetic moment of AS.

Fig. 4. Gauss-ampere characteristics for different currents of the longitudinal AS under the longitudinal magnetic field.

M_AS = ΣⁿM_n = nM_e, where M_e is the magnetic moment of a turn, n is the number of turns. The magnetic moment of an electron spinning around the hole with the rate f will be: M_e = – I_eS = – ef S, where S = πL_e² is the area of an electron turn.

M_e = – µ₀e²L_e²H₀ 2m_e                      (1)

The magnetic moment direction of a turn generated by the spinning of radially moving electron in the AS under the external longitudinal magnetic field is shown in Fig. 5. When the direction of the external magnetic field is such as shown in Fig. 5a, the Lorentz force, in accordance with the left-hand rule, is directed in such a way that a circular current triggered by the electron rotation flows in a clockwise order, what, in compliance with the right-hand screw, provokes the appearance of the magnetic moment oppositely directed to the external magnetic field. A change in the direction of the external magnetic field H₀ into the opposite (Fig. 5b) entails the variation of the turn magnetic moment. So, the directions of induced magnetic moment M_e in AS and the external magnetic field, as could be expected, are oppositely directed.

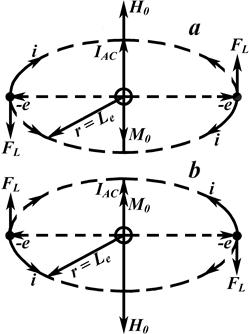
Fig. 5. The appearance of the diamagnetism in the longitudinal AS under external longitudinal magnetic field H₀.

Radii of spinning electrons will be 0 ≤ r ≤ L_е by virtue of the spread of diffusing electron directions. Let`s change this inequality with the concept of the average radius of spinning electrons. We consider an AS cell with sizes as follows: a cell radius is r = L_е, a cell height is h = L_e. The volume of the cell is νc = πL_e³. The number of electrons in the cell is n_с = n_eν = πL_e³n_e, n_e is the specific concentration of electrons in AS. The unit radius of a spinning electron in this cell is r_k = L_еcosα_k, where α_k is the angle between the diffusing electron direction and the plane perpendicular to the AS current direction. The number of turns k can be taken as the number of electrons since we allow for only the num­ber of electrons irrespective of the orbit number, i.e. k = n_e. α_k = m(π2 k), where m is a direc­tion number from 0 to k, (π2 k) = π 2. Averaged radius is =_kk = L_е (π2k)]k. Numerical calculations (π 2k)] k yield a value of 0.637, whence it follows 0,637L_е. The magnetic moment of spinning electrons for the considered cell is M_c = M_en_c = – (µ₀e²²H₀ 2m_e)∙πL_e³n_e = – 0.2πµ₀e²L_e⁵n_e H₀ m_e. The magnetic moment of spinning electrons for all AS is:

– 0.2πµ₀e²L_e⁴ln_e H₀  m_е          (2)

A magnetization J₀ of AS gets:

J₀ν = πL_e²l = – 0.2µ₀e²L_e²n_e H₀  m_е = – 0.2αH₀ ,                                (3)

Where α = µ₀e²L_e²n_е  m_е

A magnetic induction of AS becomes:

B₀ = H₀ + J₀ = (1 – 0.2α)H₀                 (4)

Let`s take 1 – 0.2α = µ_АS, where µ_АS is the magnetic permeability of AS.

We write B₀ = µ_АS ∙H₀.

An additional diamagnetic moment of electrons appeared at the application of the external mag­netic field to spinning electrons is [18]:

M_e^d = – µ₀e²r²B₀ 4m_е                     (5)

In case of H = H₀ r = L_e. However, the spinning electron radii are r_k = L_еcosα_k because of the spread of diffusing electron directions. Since the angular rate variation of the electron turn in the orbit is similar for all electrons irrespective of their orbit radii and linear travel we can employ the concept of the averaged radius. Following the preceding reasoning and allowing for the unit cell with a height of h = L_е, a square of S = πL_e², we change r_k   into the averaged radius 0,637 L_е. We yield:  M_c^d = – 0.4µ₀e²L_e²n_cB₀ 4m_е = (– 0.4µ₀e²L_e²B₀ 4m_е ) πL_e³n_e= – 0.1πµ₀e²n_e L_e⁵B₀  m_е. The diamagnetic moment of spinning electrons for whole AS becomes:

M_АS^d = M_c^d(lL_e) = – 0.1πµ₀e²L_e⁴ln_eB₀  m_е       (6)

Determine the diamagnetic moment per AS unit volume, i.e. a diamagnetic magnetization J_d  of AS. It will be equal to the quotient of the whole AS induced diamagnetic moment and the AS volume ν = πL_e²l.

J_d = M_AS^d/ ν = – 0.1µ₀e²L_e²n_eB₀ / m_е = – 0.1αB₀     (7)

A magnetic susceptibility for the diamagnetic effect of AS is evaluated by an expression:

χ_d = J_d B₀ = – 0.1α                            (8)

At the outset of the presentation, we suggest the physical nature of the AS diamagnetism is simi­lar to the nature of the diamagnetism atom like an electron systems moving around the nu­cleus in specified closed orbit. For simplicity, it is usually assumed that one electron moves in an orbit with an angular rate ω = 2πf. If the magnetic field is applied to spinning electron, the angu­lar rate varies and the orbital radius remains unaltered. A change in the angular rate leads just to the generation of the magnetic moment M_d and motivates always negative susceptibility.

We get expressions for the AS magnetic moment (2), AS magnetization (3), AS diamag­netic moment (6), diamagnetic magnetization (7), and AS diamagnetic susceptibility (8) in the longitudinal magnetic field at such a value of H₀, when the cyclotron radius of electron spinning becomes equal to the diffusion length L_e and the turn of spinning electrons appears as a closed cycle. The Larmor radius of the electron spinning will decrease with an increase in the longitudi­nal magnetic field strength. One can find such a value of the magnetic field H₂, at which we obtain two closed cycles at the electron diffusion length L_e during the lifetime of electron τ_e: 2πL_e = 2πr₂+2πr₂, where r₂ = L_e2. It is known, r₂ = m_еυ_d  eH, υ_d = 4πr₂  τ_е = 4π L_е  2τ_е. From the condition of the cycle closeness we derive: r₂ = 4πm_еr₂  eτH₂, H₂ =4πm_е  eτ_е = 2H₀. Write the expression (1) at a value of the magnetic field strength H₂ = 2H₀, when L_e=2r₂: M_e = – µ₀e²∙r₂ ²H₂ 4m_е = – µ₀e² (L²_e 2²) ∙2H₀ 4m_е = – µ₀e²L_e²2H₀2 ²4m_е. Further increasing of the  longitudinal magnetic field strength produces the occurrence of three, four, n cycles of the  elec­tron spinning in the AS, and correspondingly, we get:

M_en = – µ₀e²L_e²nH₀ n ²4m_е = –   (1′)

The values of the magnetic field strength are: H_n= nH₀, n = 1, 2, 3…n.

Correspondingly, an expression for  M_ASn  is:

H_nm_e  = ()        (2′)

The AS magnetization becomes:

J_nν = – 0.2µ₀e²L_e²n_e  m_е = – 0.2α   (– 0.2α                                (3′)

The magnetic induction is written as:

B_n = H_n + J_n =(1 – 0.2α)H_n = µ_ASn H_n,       (4′)

Where µ_ASn = 1 – 0.2α

The electron diamagnetic moment in AS at =  is:

M_еn^d   = µ₀e²(L_e /n)² B_n 4mе                            (5′)

M_cn^d = – 0.4µ₀e²(L_e /n)²  B_n 4m_е =   B_n m_е = B_n m_е

The diamagnetic moment of the whole AS at =  is expressed as:

M_АSn^d = M_cn^d  =  B_n m_е   (6′)

The diamagnetic magnetization becomes:

J_n^d– 0.1µ₀e²L_e²n_eB_n  m_e =– 0.1α B_n                                   (7′)

The diamagnetic susceptibility in this case is defined by an expression:

χ_n=  = – 0.1α                       (8′)

For each AS the n_e is a particular value. The specific carriers concentration in the longitudinal AS can be derived from n_АS = I_АSl  Seµ_aV (I_АS = jS = Sen_АSµ_aE), where I_АS is the AS current, l is the sample length, S = πL_e² is the area of AS transversal section, V = lE is the electric field strength applied to the sample, µ_a is the ambipolar mobility of carriers. µ_a = 2µ_е(µ_е+µ_р), µ_е ≈ 100µ_р, then µ_а = 2µ_р. Consequently, n_АS = I_АSl  2Seµ_рV. The specific carriers concentration involving in the AS conductivity is n_е = n_АS 2 = I_АSl  4Seµ_рV. In accordance with that, the magnetic moment of the cell is: M_c  = – µ₀eL_e³lI_АSH₀ 20µ_рV.  The magnetic moment for the whole AS is:

M_АS  = M_c ∙ (l  L_e ) =  µ₀eL_e²l²I_ASH₀²  20m_еµ_рV     (2′′)

Then the AS magnetization is equal to:

  =  =              (3′′)

With n_е = I_АSl  4Seµ_рV, in mind, the previous expression can be written as:  , where    =  .

We have:  = ∙10^-7kg∙m/k², е = 1.6∙10^-19k,  = 10^-3 сm = 10^-5m, l = 0.05 сm = 5∙10^-4m,  = 8.7∙10^-3 А,  = 0.03∙9.1∙10^-31kg,  = 1694 сm²/ V∙s = 0.1694 m²/V∙s, V = 0.97 V. The calculations of expressions for the AS magnetization  (3′), AS magnetic induction B_n (4′), diamag­netic magnetization J_n^d(7′) and diamagnetic susceptibility (8′) yield following values at H₁ = H₀ = 2000 А/m (n = 1),  =  6.2∙ 10³ А/m, B₁ =  4.8∙10³ А/m,  6.5 ∙ 10³ А/m, χ₁= 1.56. The evaluation of the expression for the AS magnetic induction B₀ = (1 – 0.2)H₀ shows that it becomes equal to zero at  = 4.25 ∙ 10¹⁶сm^-3, i.e. the value of the induced magnetic field in the AS achieves the value of the external magnetic field H₀. It should be noted, however, the existence of AS is failure at such a concentration of electrons. When increasing the applied magnetic field H_n the AS magnetization  fast falls (~ 1/n), Fig. 6a, the AS magnetic induction B_n first decreases in the range of negative values, Fig. 6b, passes the zero value at n = 0.2 when the magnetic permeability is µ_АSn = 0, next increases with a value close to H_n, since µ_АSn → 1. When increasing the external magnetic field H_n, the AS magnetic magnetization J_n^dfirst rapidly decreases (~ 1/n³) in the positive value range and tends to the zero in the negative range (~ 1/n), Fig. 6c. The derived considerable value for the AS diamagnetic susceptibility (χ= 1.56 at H = H₀) is caused by a large dimensions of electron spin orbits (r ~ 10^-3 сm), in the longitudinal magnetic field. Nevertheless, the AS diamagnetic susceptibility conditioned on the magnetic field (8′), rather quickly decreases (~ 1/n²) with a rise in the magnetic field H_n, Fig. 6d, and at H_n ≈ 7.96 ∙ 10⁵ А/m becomes comparable to the diamagnetic susceptibility (χ ~ 10^-5) of a regular magnetic.

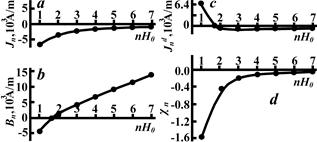
Fig. 6. Characteristics of longitudinal AS magnetic properties under external longitudinal magnetic field nH₀ (H₀ = 2000 A/m).

4. Conclusions

So, the longitudinal thermodiffusion AS formed in the non-equilibrium electron-hole plasma in p-InSb under the external longitudinal magnetic field is shown to gain diamagnetic properties. The point of departure for this statement is the diffusion of electrons for considerable distance from the axis of AS current filament stemmed from a high mobility in regard to holes in the thermodiffusion AS. In the longitudinal magnetic field, the electrons spin around the central hole-enriched region forming the closed orbits and create the magnetic moment M_e. All orbits are mutually parallel and in total define the general magnetic moment of the whole AS M = ∑ M_e.

The phenomenological treatment of the problem allows obtaining the expressions as follows:

The AS magnetization in the external magnetic field:

J_n (– 0.2α ;

The AS magnetic induction in the external magnetic field:

B_n = (1 – 0.2α)H_n = µ_ASnH_n;

The AS diamagnetic magnetization in the external magnetic field:

J_n^d– 0.1α · B_n  ;

The AS diamagnetic susceptibility in the external magnetic field:

χ_n=  = – 0.1α  ,

where α = µ₀e²L_e²n_е  m_е =  .

The computation of the diamagnetic susceptibility χ_nand its estimation provide the large value of χ= 1.56 at H₀, primarily, stemmed from large dimensions of electron spinning orbits (r ~ 10^-3 сm), in the AS in the longitudinal magnetic field. Though, when increasing the external mag­netic field H_n, the orbit radii vigorously decrease what leads to the same decreasing (~1/n²) in the diamagnetic susceptibility.

References

1. S.V. Vonsovskii. Magnetizm. Izdatel'stvo «Nauka», Moscow, 1971, p.1032.
2. A.A. Stepurenko, Fiz. Tekh. Poluprov. 28, 402 (1994).
3. A.A. Stepurenko, Fiz. Tekh. Poluprov. 30, 76 (1996).
4. B.S. Kerner and V. V. Osipov, Sov. Phys. JETP 36, 359 (1982).
5. V.A. Vashchenko, B.S. Kerner, V.V OsipovandV.F. Sinkevich.Fiz. Tekh. Poluprov., 23, 1378 (1989).
6. T. Hayashi, T. Morita, M. FukayaandE. Hasegawa. Japan J. Appl. Phys., 13. № 10. 1667 (1974).
7. B.S. Kerner, V.V Osipov, M.T. Romanko, V.F. Sinkevich.Sov. Phys. JETP, 44, v. 2, 77 (1986).
8. M.N. Vinoslavskii.Fiz. tverd. Tela., 31, 315 (1989).
9. R. Symanczyk, E. PieperandD. Jäger. Phys. Lett. A, 143, 337 (1990).
10. R. Symanczyk, S. GaelingsandD. Jäger. Phys. Lett. A, 160, 397 (1991).
11. I.K. Kamilov, A.A. StepurenkoandA.S.Kovalev.Fiz. Tekh. Poluprov., 36, 187 (2002).
12. C. Hilsum and A. C. Rose-Jnnes, Semiconducting III – V Compounds., Pergamon Press. Oxford / London / New York / Paris. 1961, (p.323).
13. A.K. ZvezdinandV.V. Osipov.JETP, 58, 160 (1970).
14. I.K. Kamilov, A.A. Stepurenko, A.E. GummetovandA.S. Kovalev.Fiz. Tekh. Poluprov., 42, 393 (2008).
15. I.K. Kamilov, A.A. Stepurenko, A.E. GummetovandA.S. Kovalev.Fiz. Tekh. Poluprov., 41, 286 (2007).
16. I.K. Kamilov, A.A. StepurenkoandA.E. Gummetov.  Fiz. Tekh. Poluprov., 45, 456 (2011).
17. I.K. Kamilov, A.A. StepurenkoandA.E. Gummetov.Fiz. Tekh. Poluprov., 44, 721 (2010).
18. YU.K. Shalabutov. Vvedeniye v fiziku poluprovodnikov. Izdatel'stvo «Nauka», Leningrad, 1969, p.292.