Numerical Simulation of Water Droplet Falling onto a Liquid Pool Under Zero Gravity Conditions Using Level Set Method

Ashraf Balabel^*

Mechanical Engineering Dept., Faculty of Engineering, Taif University, Al-Haweiah, Taif, Saudi Arabia

Abstract

The present paper presents a numerical simulation of a water droplet falling under a constant velocity onto a liquid pool. The governing equations are solved using the control volume approach on a non-staggered grid system. The topological changes of the liquid droplet and the liquid surface are predicted by means of the level set method. The obtained results showed that the numerical method developed is capable to predict the resulting dynamics of such complex phenomenon in a simplified and accurate way. The remarkable capability of the developed numerical method in predicting two-phase flow dynamics enables us to predict further a wide range of two-phase flow industrial and engineering applications.

Keywords

Droplet Dynamics, Level Set Method, Zero Gravity, Numerical Simulation, Two-Phase Flows

Received: May 15, 2015
Accepted:June 3, 2015
Published online: July 15, 2015

@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/

1. Introduction

Two phase flow are encountered in a wide range of industrial as well as engineering applications, e.g. bubble and droplet dynamics [1], atomization and spray of liquid jet [2], and other multiphase flow systems [3]. Due to the importance of droplet dynamics in most of two-phase flow systems, there is an increased attention being given for the prediction of deformation and disintegration of droplets either numerically, analytically or experimentally. It is well known that the combustion efficiency in diesel engines, gas turbine engines, oil burners and liquid rockets is strongly dependent on liquid fuels atomization process [4].

Consequently, two-phase flow remains a challenging topic of research [5] due to the existence of interfacial surface force such as surface tension and shear stress. Such stresses usually interact with other mechanisms, such as surface instabilities, ligament formation, stretching and fragmentation to transform large scale coherent liquid structures into small scale droplets [6].

The numerical simulations of the two-phase dynamics are scarcely due its computational challenges [7,8]. Although drops seldom occur in isolation, it is essential to understand the behavior of single and binary droplets before a full knowledge on interacting can be achieved. Disturbances, which cause disintegration of drops, include: rapid acceleration and high shear stresses.

Although several papers have recently reported experimental efforts to understand the physics of the droplet deformation, disintegration and its related dynamics in two-phase flow, however, experimental measurements and the observation of dense and small region with high spatial-temporal resolution in such applications have been difficult [9].

In the numerical simulation of droplet dynamics, it has been difficult to predict the physical processes occurred due to the requirement of high resolution, especially for high Weber and Reynolds number. The severe resolution required in such simulation is essentially in order to resolve the important role played by surface tension in ligament and drop formation. Consequently, in order to obtain an insight in such dynamics, the numerical treatments of such processes are carried out in a number of sequential steps starting from the investigation of the surface instability that leads to droplet deformation followed by ligament formation and drop separation from a single ligament till the secondary break-up of liquid droplets.

More recently, carefully executed simulations in such context can virtually replace experiments. In general, the numerical predictions of droplet dynamics have been limited in accuracy partly by the performance of three key elements, viz.: development of the computational algorithm, interface tracking methods, and turbulence prediction models.

During the last decade, a variety of computational fluid dynamics techniques have been developed to study two-phase flow dynamics. A comprehensive review of the numerical models applied for two-phase flow up to 1996 can be found in [10]. More extended review up to 2010 for the atomization process and its related dynamics can be found in [11].

Usually, in the numerical simulation of two-phase flows, the Navier-Stokes equations are coupled to one of the available tracking methods in order to predict the complex topological changes of the phase interface, see for more details [12,13]. Given examples for such tracking methods, Volume-Of-Fluid (VOF) method [14] and Level Set Method (LSM) [15] are the most popular interface capturing methods. Although the VOF method has been widely applied for predicting different complex two-phase flows, it suffers from several numerical problems such as interface reconstruction algorithms and the difficult calculation of the interface curvature [16]. These numerical problems can, in particular, limit the accuracy and the stability of the numerical method adopted for calculation of two-phase flows, especially when the surface tension is included. A comprehensive review for the different VOF methods and their numerical constraints can be found in [17].

In contrast to the VOF methods, the level set methods offer highly robust and accurate numerical technique for capturing the complex topological changes of moving interfaces under complex motions. The basic idea of LSM is the use of a continuous, scalar and implicit function defined over the whole computational domain with its zero value is located on the interface. The LSM divides the domain into grid points that contain the value of the scalar function; therefore, there is an entire family of contours. The interface is then described as a signed distance function at any time and, consequently, the geometric properties of the highly complicated interfaces are calculated directly from level set function. Moreover, the complex topological changes of interfaces such as merging and breaking-up are handled automatically in a quite natural way without any additional procedure. In addition, the extension of the LSM to three-dimensional problems is easy and straightforward.

Referring to the previous discussion, the LSMs have seen tremendously in different CFD-applications of diverse areas, e.g. two-phase flows, turbulent atomization, grid generation and turbulent combustion [18]. However, the LSMs suffer from numerical diffusion which may cause a smoothing out of sharp edges of interface. The level set function is usually evolved by a simple Eulerian scheme and, consequently, the final implementation of LSM does not provide full volume conservation, so highly accurate transport schemes are required. In our previous work [19-27], a new technique for solving the level set equation has been developed and validated by performing a number of challenge test cases.

The problem under consideration is extensively reviewed in [28], where the different regimes encountered in the impinging process of a droplet on a liquid surface is numerically investigated. A regime map is established for Weber numbers ranging from 50 to 300 and Froude numbers from 25 to 600. However, in the present numerical simulation we consider the Weber number, We=300 and the Froud number equals zero.

2. Governing Equations

The problem under consideration can be shown in Fig.1, where a free droplet falls with an initial velocity onto a liquid pool, initially with a specified length L and a water height H. The diameter of the droplet is denoted by D, where the distance between the droplet and the water surface is given by H_d.

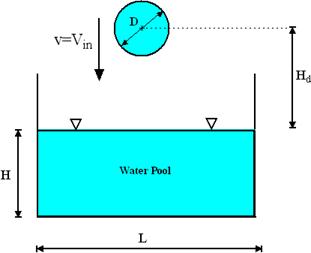
Figure 1. The configuration domain of falling droplet onto liquid pool.

The governing equations for incompressible two-phase flow are mathematically expressed by the conservation equations of the mass and momentum at each point of the flow field. These equations can be written in the primitive variables formulation in form of continuity equation and Navier-Stokes equations, respectively, as follows:

                                            (1)

                 (2)

where r, u, p, m are the density, velocity vector, pressure and viscosity of the fluid. The subscript i denotes the liquid phase (i=1) and the gas phase (i=2), respectively. It is known that, for two–phase flows, the pressure and velocity field inside the droplet are caused by the external gas stresses in the tangential and normal directions. Therefore, the dynamic balance between both phases can be obtained by solving the complete set of the governing equations in the gas phase for the velocity and pressure around the droplet surface and using these values as boundary conditions for solving the interior droplet phase to specify the exact level of pressure and velocity components inside the droplets. The obtained normal velocity component at the droplet interface is then used to obtain the topological changes and deformation of the droplet surface via the level set method.

The fact that there is no pressure transport equation necessitates the consideration of the continuity equation as a means to obtain the correct pressure field. This is done by a proper coupling between the pressure and velocity field through the Poisson equation for pressure:

                     (3)

The Poisson equation is solved by means of the Successive Over-Relaxation method in each phase to obtain the pressure level inside the considered phase.

In our algorithm, the implicit fractional step-non iterative method is applied to obtain the velocity and pressure filed by presuming that the velocity field reaches its final value in two stages; that means in each phase the following algorithm is applied:

                                      (4)

where by,  is an imperfect velocity field based on a guessed pressure field, and  is the corresponding velocity correction. Firstly, the 'starred' velocity will result from the solution of the momentum equations. The second stage is the solution of Poisson equation for the pressure:

                                     (5)

where  will be called the pressure correction. Once this equation is solved, one gets the appropriate pressure correction, and consequently, the velocity correction is obtained according to:

                                     (6)

This fractional step method described above ensures the proper velocity-pressure coupling for incompressible flow fields, see for more details [27].

3. Level Set Method

Generally, the numerical simulations of two-phase flow could become quite challenging problem and face significant difficulties. In particular, an accurate tracking of complex interfaces, where large deformations and inter-penetration of phases occur, is required. In addition, the basis of improving such numerical simulations lies in satisfying the interface- normal and tangential stress boundary conditions more accurately.

In order to describe the complex topological changes of the interface separating the two phases with an elegant, robust and efficient method, the level set approach is applied. Since the original work of the level set method introduced in [8], a large amount of bibliography on this subject has been published and several types of problems have been tackled with this method; for instance one can see the cited review [11,12] and the more recent developments of the level set method [27].

In the formulation of the level set, a smooth function f is typically initialized as a signed distance function from the interface, i.e., its value at any point is the distance from the nearest point on the interface and its sign is positive on one side and negative on the other. Let us set f as positive in liquid and negative in gas. The location of the interface is then given by the zero level set of the function f. In absence of the interfacial mass transfer such as evaporation or condensation, the equation of the level set method can be written as:

                           (7)

From the level set function, the normal vector and the interface curvature can be calculated as:

                                 (8)

It should be pointed out that, the curvature of the interface is calculated only on the main grid points. However, the exact curvature should be calculated at the interfacial markers located on the intersection points of the computational grid with the interface. Consequently, the interpolation scheme applied for obtaining the fluid variables at the interface is also applied for calculating the interfacial curvature, for more details one can see [27]

By projecting the velocity vector onto the direction normal to the interface, and by using the definition of the normal vector described above, the level set equation becomes

                               (9)

A variety of methodologies have been proposed for solving the above advection equation of the level set function. One of the most recently developed numerical methods is proposed in [27]. In this method the normal velocity V_n in Eq. (15) is replaced by some velocity field F_ext known as the extension velocity, which at the zero level set G, equals the given speed V_n. In other words, the level set equation can be written as:

                                (10)

where,

                                     (11)

The present time-stepping procedure applied for the level set equation is based on the second-order Runge-Kutta method. An important step in the solution algorithm of the level set function is to maintain the level set function as a distance function within the two fluids at all times, especially near the interface region, i.e. the Eikonal equation,, should be satisfied in the computational domain. That can be achieved each time step by applying the re-initialization algorithm described in [8] for a specified small number of iterations.

4. Result and Discussions

Figure 2 shows important dynamics of the considered problem of droplet falling onto a liquid pool. It can be seen that as the droplet approaches the liquid surface, both of the droplet and the liquid surface are deformed.  The deformation is continued after the impact process until the droplet is completely falls inside the liquid pool. The water surface forms a nearly sinusoidal waveform. After that, the water surface continues deformation until it reaches to the flat interface form due to the existence of the surface tension force.

Figure 3, shows the velocity vectors plot at later stage of the deformation process of the water surface where it can be seen the existence of different recirculation zones outside and inside the liquid surface. The recirculation zones are responsible for the final deformation of the water surface.

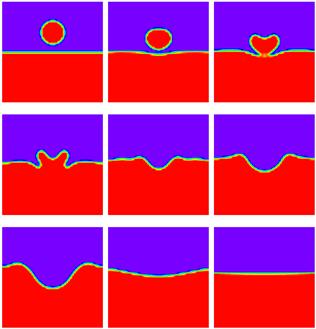
Figure 2. The predicted dynamics of falling droplet onto liquid pool.

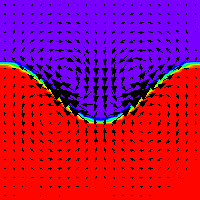
Figure 3. Velocity vectors in both phases after impact process.

After completion of the impact process, the water surface increases with a small amount according to the additional mass of the impact droplet. This can be seen in Fig. 4., where the height of the initial water surface increases with a specified height according to the mass of the initial droplet.

The most important parameter during the present numerical simulation is the mass lost from the droplet and the water surface due to the numerical diffusion error. This parameter controls the accuracy of the numerical simulation of two-phase flow, especially, when a level set method is applied for tracking the moving interface. Figure 5 shows the transient mass of the droplet in addition to the water quantity made dimensionless by the initial mass. The figure shows that the mass lost is about 0.01 of the initial mass during the complete numerical simulation and that can be considered in the accepted range of the numerical errors.

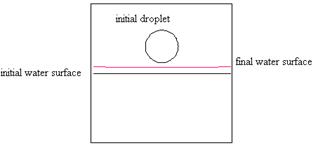
Figure 4. Comparison of the initial and final water surface level.

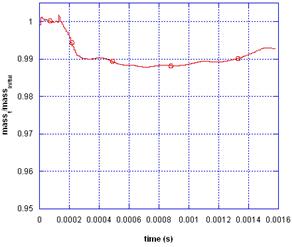
Figure 5. The loss of droplet mass during the numerical simulation.

5. Conclusions

In the present paper, one of the most important problems of two-phase flow is numerically simulated; namely, the falling of a single droplet onto liquid pool under zero gravity conditions. The governing equations are solved by the control volume approach while the moving interfaces are tracked with the level set method. The numerical results showed a remarkable accuracy of the developed numerical method. That can be extended further to include much more complex geometries of two-phase flow applications.

References

1. Fuster, D., Agbaglah, G., Josserand, C., Popinet, S. and Zaleski, S., Numerical simulation of droplets, bubbles and waves: state of the art, Fluid Dyn. Res. 41: 1-24, 2009.
2. Lefebvre, A. H., Atomization and sprays, Hemisphere Publishing Corporation, 1989.
3. Kolev N.I., Multiphase flow dynamics: Thermal and Mechanical Interaction", Springer, 2007.
4. Yang V., Habiballah M., Hulka J. and Popp M., Liquid Rocket Thrust Chambers: Aspects of Modeling, Analysis, and Design", American Institute of Aeronautics and Astronautics, Inc., 2004.
5. Linne M., Paciaroni M., Hall T., and Parker T., Ballistic imaging of the near field in a dense spray", Exp. Fluids., 49(4): 911-923, 2006
6. Menard T., Tanguy S. and Berlemont A., Coupling level set/VOF/ghost fluid methods: Validation and application to 3D simulation of the primary break-up of a liquid jet, Int. J. Multiphase Flow, 33: 510-524, 2007.
7. Desjardins, O., Moureau, V. and Pitsch, H., An accurate conservative level set/ghost fluid method for simulating turbulent atomization, Journal of Computational Physics, 227: 8395–8416, 2008.
8. Sussman, M. , Smereka, P. and Osher, S., A level set approach for computing solutions to incompressible two-phase flows, J. Comp. Physics, 114, 146-159, 1994.
9. Eggers, J., Nonlinear Dynamics and Breakup of Free-Surface Flow, Rews. Modern Phys., 69(3): 865–929, 1997.
10. Crowe C. T., Troutt T. R. and Chung J. N., Numerical models for two-phase turbulent flows", Annu. Rev. Fluid Mech., 28:11-43, 1996.
11. Shinjo J. and Umemura A., Simulation of liquid primary breakup: Dynamics of ligament and droplet formation", Int. J. Multiphase Flow, 36(7): 513-532, 2010.
12. Osher, S. and Fedkiw, R. P.., Level set methods: An overview and some recent results, J. Comp. Phys., 169, 463-502, 2001.
13. Sethian, J. A. and Smereka, P., Level set methods for fluid interfaces, Annu. Rev. Fluid, Mech., 35, 341-372, 2003.
14. Nichols B. D. and Hirt C. W., Methods for calculating multi-dimensional, transient free surface flows past bodies, Proc. First Int. Conf. Num. Ship Hydrodynamics Gaithersburg, 20–23, 1975.
15. Osher S. and Sethian J. A., Fronts propagating with curvature-dependent speed: algorithms based on Hamilton–Jacobi formulations, Journal of Computational Physics, 79: 12–49, 1988.
16. Li, Z., Jaberi, F. A. and Shih, T., A hybrid Lagrangian–Eulerian particle-level set method for numerical simulations of two-fluid turbulent flows, Int. J. Num. Methods in Fluids, 56: 2271-2300, 2008.
17. Scardovelli, R. and Zaleski, S., Direct numerical simulation of free-surface and interfacial flow, Annu. Rev. Fluid Mech., 31: 567–603, 1999.
18. Peters N., Turbulent combustion", Cambridge University Press, Cambridge, UK, 2000.
19. Balabel, A., Binninger, B., Herrmann, M., and Peters, N., Calculation of Droplet Deformation by Surface Tension Effects using the Level Set Method, Combust. Sci. Technology, 174(11-12): 257–278, 2002.
20. Balabel A., Numerical prediction of droplet dynamics in turbulent flow, using the level set method, International Journal of Computational Fluid Dynamics, 25(5): 239-235, 2011.
21. Balabel, A., Numerical simulation of two-dimensional binary droplets collision outcomes using the level set method, International Journal of Computational Fluid Dynamics, vol. 26, no. 1, pp. 1-21, 2012.
22. Balabel, A., Numerical modeling of turbulence-induced interfacial instability in two-phase flow with moving interface Applied Mathematical Modelling, vol. 36, pp. 3593–3611, 2012.
23. Balabel, A., Numerical Modelling of Turbulence Effects on Droplet Collision Dynamics using the Level Set Method. Computer Modeling in Engineering and Sciences (CMES), vol. 89, no.4, pp. 283-301, 2012.
24. Balabel, A., Numerical modeling of turbulence-induced interfacial instability in two-phase flow with moving interface, Applied Mathematical Modelling, vol. 36, no. 8, pp. 3593-3611, 2012.
25. Balabel, A., Numerical prediction of droplet dynamics in turbulent flow, using the level set method. International Journal of Computational Fluid Dynamics, vol. 25, no. 5, pp. 239-253, 2012.
26. Balabel, A., Numerical Modelling of Liquid Jet Breakup by Different Liquid Jet/Air Flow Orientations Using the Level Set Method, Computer Modeling in Engineering and Sciences (CMES), vol. 95, no.4, pp. 283-302, 2013.
27. Balabel, A., A Generalized Level Set-Navier Stokes Numerical Method for Predicting Thermo-Fluid Dynamics of Turbulent Free Surface. Computer Modeling in Engineering and Sciences (CMES), vol. 83, no. 6, pp. 599-638, 2012.
28. Bahni R., Gautam B. and Ashutosh S., Regimes during liquid drop impact on a liquid pool, J. Fluid Mech., vol. 768, pp. 492-523, 2015.