Algebraic Studies for Electronic Structures and Photodissociation of Bromine Molecule
A. Abdel-Hafiez*
Department of Experimental Nuclear Physics, Nuclear Research Center, Atomic Energy Authority, Cairo, Egypt
Abstract
I have theoretically studied the nonadiabatic transitions among the lower states with W=1u symmetry (1u(1) to 1u(3)) in the photodissociation of Br2 using the Comlete Active Space Self-Consistent Field (CASSCF) computations and the time-independent SchrÖdinger equations. The CASSCF wave function is formed from a complete distribution of a number of active electrons in a set of active orbitals, which in general constitute a subset of the total occupied space. From the configuration analysis of the CASSCF wavefunctions, we found that the nonadiabatic transition between 1u(2) and 1u(1) is a noncrossing type, while that between 1u(2) and B3P0+u is a crossing type. The spectroscopic constants for the X1Sg+, A3P1u and B3P0+u states of Br2 is calculated. The absorption cross-section for the ground and the lower excited states in the photodissociation of Br2 molecule is presented as well as the numerical estimates of nonadiabatic transition probabilities. Also, the five highest occupied and the five lowest unoccupied orbitals of Br2 have been calculated.
Keywords
Algebraic technique / Quantum dynamics/ Electronic structure
Received: February 26, 2015
Accepted: March 7, 2015
Published online: March 12, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
Classical investigations of the discrete absorption spectrum of halogen molecules, specially Br2 and I2, have resulted in the accurate identification of transitions between specific vibrational and rotational levels of these diatomics1. Such analyses have permitted the precise characterization of the potential curves for the bound X1Sg+ ground and B3P0+u excited states. A drawback, common to the above methods, is that such techniques cannot, however, to be used for the study of repulsive states or those portions of bound excited states which lie above the thermochemical threshold for dissociation into open-shell atomic fragments in ground configuration with which they correlate.
Diatomic halogen and interhalogen molecules continue to serve as benchmark systems to study photodissociation dynamics. Recent experimental activity has been devoted to the study of the orientation and alignment, namely the mj distributions, of the product angular momentum. Details of the nonadiabatic transition probabilities have been estimated from such analysis for Cl22-5 and Br24. Also, recent advances in both experimental and theoretical studies of molecular photodissociation enable us to investigate quite detailed information on the dissociation dynamics.
Yukako Asano and Satoshi Yabushita6 calculated the potential curves of I2 by the spin-orbit configuration interaction (SOCI) method, and evaluate the radial derivative coupling elements among the five lower states with W=1u symmetry (1u(1) to 1u(3)) to examine the nonadiabatic transition processes and to compare the results with those of Cl2 and Br2. Also, Yukako Asano and Satoshi Yabushita5 evaluated the nonadiabatic transition probabilities of Cl2 and Br2 by solving the semiclassical time-dependent coupled SchrÖdinger equations.
Balasubramanian et al.7 calculated the spectroscopic properties and potential curves of I2 by the complete active space SCF method followed by the nonrelativistic first-order and second- order configuration interaction (CI), and rtecent relativistic many-body perturbation methods. Teichteil and Pelissier8 calculated the potential curves of I2 with an ab initio relativistic atomic pseudo- potential method and analyzed the available experimental data. Nieuwpoort et al.9 employed an all-electron Dirac- Fock method followed by the CCSD(T) calculations. However, none of the previous workers has studied the nonadiabatic transitions in the photodissociation of I2.
The ability to accurately describe complicated molecular wave functions with only few terms has often been claimed to be one of the major advantages of the MCSCF mrthod10. This simple picture is usually contrasted to the very long expansions encountered in conventional CI methods where the orbitals are not variationally optimized. In the CASSCF method, the philosophy is quite different from that of traditional MCSCF methods, in that it should involve complete sets of multiconfigurational wave functions although it tends to be rather time consuming, thus providing an ideal path for the systematic study of electron correlation effects in excitation processes involve not only one photon.
A potential energy surface is a mathematical relationship linking molecular structure and the resultant energy. For a diatomic molecule, it is a two-dimensional plot with the internuclear separation on the X-axis, and the energy at that bond distance on the Y-axis, producing a curve. For larger systems, the surface has as many dimensions as there are degree of freedom within the molecule.
Potential energy surfaces may be determined by ab initio electronic structure calculations. In this method one performs a large number of electronic structure calculations (which may be very expensive) and then fits the results using a least square procedure. The reliability of the PES depends on the basis set completeness and how well electron correlation is accounted for.
In the paper10the CASSCF method was presented in detail. In this study, we introduce the brief discussion of the method and presents some experience from an application to the bromine molecule, we calculate the ground and some excited states of Br2 by the Comlete Active Space Self-Consistent Field (CASSCF) computations at 6-31+G(d,p) level and the semiclassical time-dependent coupled SchrÖdinger equations.
2. Computational Methods and Theory
The CASSCF program used is a part of the GAUSSIAN 0311 suite of programs. A CASSCF calculation is a combination of SCF computation with a full configuration interaction calculation involving a subset of the orbitals. The orbitals involved in the CI are known as the active space. In this way, the CASSCF method optimizes the orbitals appropritely for the excited state.
All calculations have been performed using the implementation of the CASSCF procedure and the standard 6-31+G(d,p) basis set available in the Gaussian 0311 Locations of excited-state minima and transition structures have been carried out by using the methods available in the same program package.
The numerical estimates of nonadiabatic transition probabilities are calculated by using the program of Yukako Asano and Satoshi Yabushita6. That program depends on the semiclassical theory, in which the total wavefunction ye(R(t),r) satisfies the following time – dependent Schrodinger equation
![]()
where He is the electronic Hamiltonian, r is the electronic co-ordinate, and R(t) is the internuclear distance, and the molecular rotation is not considered here. If ye is expand in terms of the adiabatic wavefunctions, 1u(1) through 1u(5), the expansion coefficients Cn(t) satisfy a set of the first-order coupled equations,
![]()
where Ek are the eigenvalues of He, u is the relative nuclear velocity, gkn= á1u(k) çd / dRê1u(n)ñ are the radial derivative (nonadiabatic) coupling elements between 1u(k) and 1u(n) and çCn(t)ê2 stands for the probability of finding the system in the adiabatic state 1u(n). The relative nuclear motion is described by the classical equation of motions.
![]() ,
,
where m is the reduced mass and Ei is the adiabatic potential energy on which the photodissociation takes place.
3. Results and Discussion
The calculated adiabatic potential curves of Br2 are shown in Figure 2. Spectroscopic constants of the X1Sg+, A3P1u and B3P0+u states of Br2 are shown in Table 1, and are in reasonable agreement with the experimental results15, 16. We thus expect that quantitative results can be obtained for the photodissociation processes with these ab initio potential energy curves.
Table 1. Our calculations in comparison with experimental spectroscopic constants15, 16 for the X1Sg+, A3P1u and B3P0+u states of Br2
| Re(Å) | De(kJ/mol) | we(cm-1) | wexe(cm-1) | ||
| X1Sg+ | This work | 2.304 | 188.53 | 320.7 | 1.24 |
| Experiment | 2.280 | 190.17 | 325.3 | 1.08 | |
| A3P1u | This work | 2.758 | 22.57 | 144.8 | 2.85 |
| Experiment | 2.690 | 24.77 | 153 | 2.7 | |
| B3P0+u | This work | 2.760 | 43.51 | 163.1 | 1.91 |
| Experiment | 2.677 | 44.96 | 167.6 | 1.64 |
Re, De, we, and wexe are the equilibrium bond length, the dissociation energy at equilibrium R for the corresponding state, vibrational frequency characterize, and the anharmonic spectroscopic constants, respectively. Our calculations for these characterestics is explored by performing a potential energy surface scan on the model chemistry CASSCF /aug-cc-pVTZ level, where the notation (10,8) defines the complete active space: 10 electrons distributed over 8 molecular orbitals (MOS) {σBr-Br*, πx(Br), πx*(Br), πy(Br), πy*(Br), 2nBr, σBr-Br}
The calculated potential curves of Br2 are shown in Fig.1. Note that the A3P1u (1u) and 1Pu (1u) states correlate to the ground state Br+Br limit, whereas the B3P0+u (0u+) state correlates to the Br+Br* limit. The potential energy curve for another repulsive 1u state, correlating to the Br+Br* limit, what it mean that potential is implicated in the propsed explanation for the non-limiting b values observed for the Br+Br* product recoil velocity distributions17
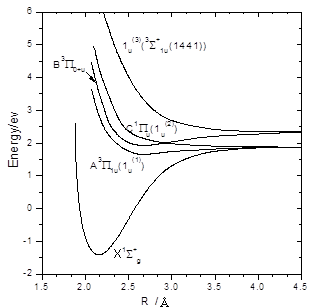
Fig. 1. Potential energy curves for ground state Br2 and for the three excited states determined by CASSCF calculations
In the numerical calculation of the absorption cross-section for the photodissociation of Br2 molecule, we used the program by Balint-Kurti et al.18 employing the time-dependent quantum dynamical method. The mechanism is assumed to involve the absorption of a photon of ultraviolet radiation which causes an electronic transition in the molecule from a bound to a repulsive electronic state. The two atoms then fly apart under the influence of the forces on the repulsive electronic state causing the molecule to break up into its atomic fragments. This program permits the calculation of cross-sections for molecules in different initial vibrational states.
Our programmed calculations of the total absorption cross section to the A, B, and C states are shown in Fig.2a, also portrayed are the partial absorption coefficients from these discrete state, which corresponding to the schematic deconvolution of the total absorption spectrum and indicate that the A-X and, particulary, B-X transitions contribute to the continuous absorption at shorter wavelengths(l<510 nm); the latter is deemed responsible for the inflexion in the absorption profile at l » 460 nm. Electronic absorption spectrum of Br2 recorded over the wavelength range 300-600 nm (solid lone),together with an illustrative decomposition into contributions associated with excitations to the A3P1u (1u), B3P0+u (0u+) and 1Pu (1u) states ( dot lines).
It also apparent that the first absorption band has a peak at 421.4 nm due to the excitation to the C1Pu (1u(2)) state and agrees well with both of ref 5in which it has a peak at 419.6 nm and the experimental value of 420 nm17,18.The calculated absorption cross section to the ![]() state in Fig.2b has a maximum at 235.3 nm, which is in reasonable agreement with both of ref6in which it has a peak at 234.8 nm and with the experiment, supporting the tentive assignment19.
state in Fig.2b has a maximum at 235.3 nm, which is in reasonable agreement with both of ref6in which it has a peak at 234.8 nm and with the experiment, supporting the tentive assignment19.
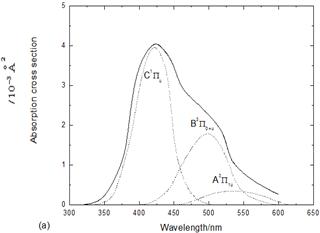
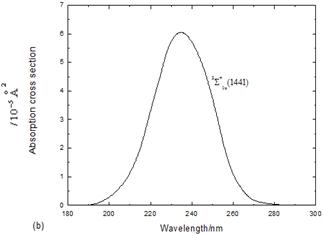
Fig. 2. (a) Absorption cross sections to the lower excited states of Br2. (b) Absorption cross section to the![]() state of Br2.
state of Br2.
Fig.3a Show the probabilities after the photoexcitation to the C1Pu(1u(2)) state at 355 nm for Br2 and the nonadiabatic transition from 1u(2) takes place only to 1u(1). Fig.3b show the probabilities after the vertical excitation to the ![]() (1u(3) ) state and the nonadiabatic transition takes place only to 1u(4).
(1u(3) ) state and the nonadiabatic transition takes place only to 1u(4).
Table 2 summarizes the low-lying excitations of the parent Br2 molecule. According to the TD-DFT computations, in both states, the transition σz(Br)® πz*(Br-Br) calculated at 8.6373 eV (143.54 nm) and nx(Br)® πz*(Br-Br), ny(Br)® πz*(Br-Br) calculated at 2.6446 eV (468.81 nm) are found to dominate the absorption from the estimated oscillator strength f=0.8774 and f=0.0004 respectively. Because the excitation energies to the σz(Br)® πz*(Br-Br) transition lies very close to the Rydberg transition, the measured spectrum band can be ascribed mainly to the transitions nx(Br)® πz*(Br-Br) and ny(Br)® πz*(Br-Br). This indicates that experimental absorption profile will show a maximum cross-section nearby the wavelength of 460 nm.
In order to help better explore the photodissociation channels correlate to the low lying excited states of Br2, we have examined the relevant molecular orbitals. Fig.4 Shows the five highest occupied and the five lowest unoccupied orbitals calculated at the TD-DFT/6-311++G(3df,2pd) level of theory.
The five highest occupied orbitals 31-33 correspond to the lone-pair of nonbonding p electrons of the bromine atoms and 34-35 correspond to the bonding p electrons of the bromine atoms. The five lowest unoccupied orbitals 36, 39, 40 correspond to the excited nonbonding p electrons of the bromine atoms, but 39 and 40 are of higher order, the unoccupied orbitals 37,38 can be described as the σ*Br-Br.

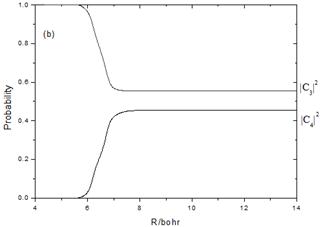
Fig. 3. Semiclassical probabilities as a function of R with 355 nm photon of Br2 from the initial excitation to the 1u(2)(C1Pu) state(Fig.3a) and from the initial excitation to the 1u(3) (![]() ) state (Fig.3b).
) state (Fig.3b).
Table 2. TD-DFT calculated excitation energies ΔE (in eV), corresponding main excitations and oscillator strengths f, for the Br2 molecule in the equilibrium geometry.
| Br2 | Main excitation | Transition energies ΔE (eV) | Excitation wavelength/ nm | oscillator strengths |
| State | ||||
| 1Πx | nx(Br)® πz*(Br-Br) | 2.6446 | 468.81 | f=0.0004 |
| 1Πy | ny(Br)® πz*(Br-Br) | 2.6446 | 468.81 | f=0.0004 |
| 1Σ- | σy(Br)® πz*(Br-Br) | 4.6611 | 266.00 | f=0.0000 |
| 1Σ+ | σx(Br)® πz*(Br-Br) | 4.6611 | 266.00 | f=0.0000 |
| 1Δ | σz(Br)® πz*(Br-Br) | 8.6373 | 143.54 | f=0.8774 |
| 3Πx | nx(Br)®πz*(Br-Br) | 1.8508 | 669.90 | f=0.0000 |
| 3Πy | ny(Br)®πz*(Br-Br) | 1.8508 | 669.90 | f=0.0000 |
| 3Σ- | σy(Br)® πz*(Br-Br) | 3.9168 | 316.55 | f=0.0000 |
| 3Σ+ | σx(Br)® πz*(Br-Br) | 3.9168 | 316.55 | f=0.0000 |
| 3Δ | σz(Br)® πz*(Br-Br) | 5.1270 | 241.83 | f=0.0000 |
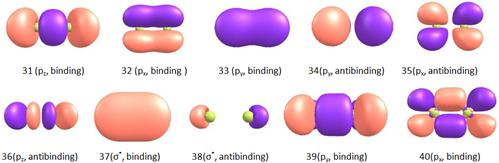
Fig. 4. The five highest occupied and the five lowest unoccupied orbitals of Br2 at TD//B3LYP/6-311++G(3df,2pd) level of theory.
4. Conclusion
We calculated the ground and low-lying excited states of Br2 by using the Comlete Active Space Self-Consistent Field (CASSCF) computations, and examined the spectroscopic constants of the X1Sg+, A3P1u and B3P0+u states which are found in reasonable agreement with experimental results. Numerical calculations of the absorption cross-section to the A, B, and C states for the photodissociation of Br2 molecule, have been done employing the time-dependent quantum dynamical approach, and agree well with experimental results. The nonadiabatic transition probabilities have been also evaluated in the frame of the semicalssical theory.
The five highest occupied and the five lowest unoccupied orbitals of Br2 could to obtain to explore the photodissociation channels at TD//B3LYP/6-311++G(3df,2pd) level of theory. Finally, we can say that CASSCF is quite good method to investigate structures on the electronic excited states and photodissociation of bromine molecule and also, produce results of high accuracy.
Acknowledgment
Many thanks to H. Studzinski, Institute for Physical Chemistry, University of Kiel, Germany for his comments and fruitful discusions.
References
- T. G. Lindeman and J. R. Wiesenfeld; J. Chem.Phys. Vol. 70, No.6, 1979, 2882]
- Bracker, A. S.; Wouters, E. R.; Suits, A. G.; Vasyutinskii, O. S. J. Chem. Phys. 1999, 110, 6749.
- Alexander, A. J.; Kim, Z. H.; Kandel, S. A.; Zare, R. N.; Rakitzis, T. P.; Asano, Y.; Yabushita, S., J. Chem. Phys. 2000, 113, 9022..
- Rakitzis, T. P.; Kitsopoulos, T. N. J. Chem. Phys. 2002, 116, 9228.
- Bass, M. J.; Brouard, M.; Clark, A. P.; Vallance, C.; Martinez- Haya, B. Phys. Chem. Chem. Phys. 2003, 5, 856.
- Yukako Asano and Satoshi Yabushita, Bull. Korean Chem. Soc. 2003, Vol.24, No. 6, 703.
- Li, J.; Balasubramanian, K. J. Mol.Spectrosc. 1989, 138, 162.
- Teichteil, C.; Pelissier, M. Chem.Phys. 1994, 180, 1.
- de Jong, W. A.; Visscher, L.; Nieuwpoort, W. C. J. Chem. Phys. 1997, 107, 9046.
- Per E.M. Siegbahn; Jan Almlof; Anders Heiberg; Bjorn O. Roos, J. Chem. Phys. 1981, Vol.74, No.4, 2384.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, et. al, Gaussian 03, Revision B.01, Gaussian, Inc., Pittsburgh PA, 2003.
- J.Paldus, in Theoretical Chemistry: Advances and perspectives, edited by H. Eyring and D. Henderson
- Complete Active Space SCF(CASSCF) and Multiconfiguration SCF (MCSCF) Wavefunctions, by Yukio Yamaguchi, Center for Computational Quantum Chemistry, School of Chemical Sciences, The University of Georgia, Athens, Georgia 30602, spring, 1996.
- Colby Chemistry, Pauel J. Schuef Computational Chemistry Lab. 2005, Holland.http://www.colby.edu.
- Huber, K. P.;Herzberg, G. Constants of Diatomic Molecules: Van Nostrand Reinhold: New York, 1979.
- Coxon, J. A. In Low-lying Electronic States of Diatomic Halogen Molecules; Barrow, R. F.; Long, D. A.; Millen, D. J., Eds.; Molecular Spectroscopy Vol. 1; The Chemical Society: London, 1973; p177
- M.J. Cooper, E. Wrede, A.J. Orr-Ewing, M.N.R. Ashfold, J. Chem. Soc. Faraday Trans. 94 (1998) 2901
- Balint-Kurti, G. G.; Mort, S. P.; Marston, C. C. Comput.Phys. Commun. 1993, 74, 289.
- S. Hubinger, J.B. Nee, J. Photochem. Photobiol. A:Chem.86(1995)1. (Academic, New York, 1976), Vol.2, p. 131.



