Thermo-Mechanical Vibration Analysis of Micro-Nano Scale Circular Plate Resting on an Elastic Medium
Titikshya Biswal, L. Bhaskara Rao*
School of Mechanical and Building Sciences, VIT University, Chennai Campus, Tamil Nadu, India
Abstract
The study of effect of temperature change and pre stress in plane load on natural frequency of single layered circular graphene sheet fixed on an elastic medium is discussed in this paper. The small scale parameters are taken into consideration to study the impact. This paper deals with classical boundary conditions such as free and guided boundary conditions. The governing differential equations of motion are derived using nonlocal plate model and newton-raphson method of numerical method solving is used to solve the corresponding equations.
Keywords
Circular Graphene Sheet, Classical Boundary Condition, Newton-Raphson Method
Received: July 9, 2015
Accepted: July 27, 2015
Published online: August 5, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
Plate structures are major load carrying elements in structural mechanics, both in aeronautics, on land and in naval engineering. Such plates are frequently subjected to significant in plane compression forces. Graphene is a new form of two-dimensional carbon nanostructure with excellent electronic and mechanical properties, holding great promise for the endless applications in numerous innovative technological fields. It is one of the new materials for the cutting edge nano-electronic devices. There is information related to its applications as mass sensor, pressure and strain sensors, atomic dust detectors and enhancer of surface image resolution. Various plate theories are available to describe the static and dynamic behavior of such plates. At nanometer scales, size effects often become prominent. So it is important to include non-local elasticity theories in the graphene sheets vibration analysis, because here small scale effects are caught by supposing that the stress at a point is a function of the strains at all other points in the domain.
Graphene which is a crystalline allotrope of carbon with two dimensional properties forms the basic structure of other allotropes like carbon nano tubes. The atoms here are arranged in a hexagonal manner, they are transparent, good conductors of heat and electricity and around hundred times stronger than steel [1]. These extraordinary properties of graphene and its contribution to nanotechnology make it an interesting and important area of study.
Effect of temperature change on fundamental frequency of micro beams and effect of elastic medium on vibration, buckling and bending of micro plates were studied by using the modified couple stress theory [2]. These are the non-classical elasticity theories. Importance of small scale effect and effects of boundary conditions on vibration of graphene sheets was studied using non-local elasticity theory. Various numerical methods were used to solve the differential equations. Non-local continuum theory [3] provided expressions for natural frequencies in case of in plane vibration of micro nano plates. They also provided the significance of non-local effect on vibration and buckling loads of graphene sheets [4]. The effect of small scale parameters, temperature change, elastic medium (both Winkler and Pasternak) [5], boundary conditions and in plane compressive load on natural frequencies and buckling of circular as well as annular graphene sheets was studied using non-local plate theory [6]. These studies provided the relation of the small scale effect and mode numbers, temperature effect and the compressive load. The frequency equations were derived for the cases of clamped and simply supported boundary conditions and solved using numerical methods of finding roots.
So far all the researches have been done on classical boundary conditions. This paper deals with some more classical boundary conditions such as free and guided and can as well be extended to non-classical boundary conditions such as elastically restrained edges against translation and elastically restrained edges against rotation. The governing differential equations of motion are derived using the nonlocal plate model and newton-raphson method of numerical method solving is used to solve the corresponding equations.
2. Nonlocal Plate Model
Nonlocal elasticity theory is significant because the stress at any location in an elastic domain is dependent not only on that location; rather it depends on strains at every other location [7]. The most general equation of motion for a nonlocal homogeneous linear elastic body is given by Eq. (1):
![]() (1)
(1)
Where,
![]() is the stress,
is the stress,
![]() is the strain and
is the strain and
![]() is the elasticity tensor of the fourth order.
is the elasticity tensor of the fourth order.
The nonlocal effect is incorporated using the nonlocal modulus ![]()
![]() is a material constant
is a material constant
![]() is a constant for approximation of results with other models. It’s the nonlocal parameter [8].
is a constant for approximation of results with other models. It’s the nonlocal parameter [8].
a is the radius of the circular plate
![]() is the external length
is the external length
The integro-differential equation (1) can be simplified to [9]:
![]() (2)
(2)
where![]()
![]() is the laplacian operator
is the laplacian operator
According to the principle of virtual work [10] the governing EOM is given as:
![]() (3)
(3)
Here,
![]() is the flexural rigidity of the SLGS
is the flexural rigidity of the SLGS
![]() is the transverse displacement of the nanoplate
is the transverse displacement of the nanoplate
![]() is the density of the plate
is the density of the plate
![]() is the boundary tension given by:
is the boundary tension given by: ![]() (load per unit length)
(load per unit length)
![]() is the resultant thermal stress given by:
is the resultant thermal stress given by: ![]()
The displacement of the plate for free vibration can be expressed in terms of polar coordinates as:
![]() (4)
(4)
Where ![]() is the natural frequency with which the circular plate oscillates.
is the natural frequency with which the circular plate oscillates.
Inserting equation (8) into equation (7) and solving using separation of variables method, we obtain the general solution as:
![]() (5)
(5)
where,
m is the mode number and ranges from 0 to n
![]() and
and ![]() are the eigen values
are the eigen values
![]() and
and ![]() are bessel functions of first and second kind of order m
are bessel functions of first and second kind of order m
![]() and
and ![]() are modified bessel functions of first and second kind of order m
are modified bessel functions of first and second kind of order m
3. Boundary Conditions
3.1. Guided Boundary Condition
Let us consider a circular nano plate of radius a sliding across two roller supports as shown in Figure 1 [11].
To avoid stresses and deflection on the center of the circular nano plate, the terms ![]() and
and ![]() should be considered as zero.
should be considered as zero.
The boundary conditions are:
![]() (6)
(6)
![]() (7)
(7)
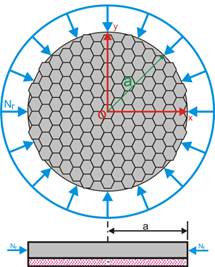
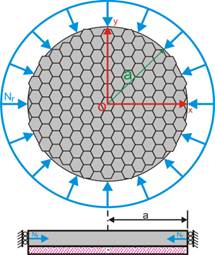
Figure 1. Nonlocal plate model of circular graphene sheet with guided and free boundary condition.
Substituting equations (6) and (7) in equation (5) and equating the determinant of the matrix to zero, the characteristics frequency equation becomes:
![]()
- ![]() (8)
(8)
3.2. Free Boundary Condition
Let us consider a circular nano plate of radius a subjected to free vibrations as shown in the Figure 1.
The boundary conditions are:
![]() (9)
(9)
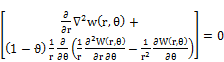 (10)
(10)
Substituting equations (9) and (10) in equation (5) and equating the determinant of the matrix to zero, the characteristics frequency equation becomes:
![]()
![]() (11)
(11)
The frequency and other non-dimensional parameters are given as:
![]() ,
, ![]() ,
, ![]() ,
,
![]()
4. Results and Discussion
Table 1. Comparison of non-dimensional fundamental natural frequencies of square and circular nano plate (simply supported BC).
| Results | (nm) | |||||||
| 0.25 | 0.5 | 0.75 | 1.0 | 1.25 | 1.5 | 1.75 | 2.0 | |
| Pradhan and Phadikar [8] | 2.000 | 1.992 | 1.969 | 1.952 | 1.932 | 1.909 | 1.857 | 1.827 |
| Mohammadi et al.[7] | 2.000 | 1.990 | 1.964 | 1.944 | 1.921 | 1.895 | 1.835 | 1.802 |
| Present | 2.000 | 1.990 | 1.964 | 1.944 | 1.921 | 1.895 | 1.835 | 1.802 |
This paper investigates the effect of thermal and small scale factors on the vibration of circular nanoplate under in-plane pre-stressed load. The small scale coefficients is assumed to be between 0 - 2.0 nm. The properties are E = 1060 GPa, υ = 0.25, ρ = 2250![]() . For room or low temperature case thermal coefficient is α = –1.6*
. For room or low temperature case thermal coefficient is α = –1.6*![]() and for high temperature case thermal coefficient is taken α = l.l*
and for high temperature case thermal coefficient is taken α = l.l*![]() . These are the values which were used for CNTs [12-14]. Single layered circular graphene sheets are considered for the present nonlocal study. The radius of the circular grapheme sheet is taken as 20 nm [9].
. These are the values which were used for CNTs [12-14]. Single layered circular graphene sheets are considered for the present nonlocal study. The radius of the circular grapheme sheet is taken as 20 nm [9].
It is seen that frequency parameters decrease as nonlocal parameter increases, implying that the there is a decrease in the stiffness of structure as the nonlocal parameter increases for a fixed value of temperature. But non-dimensional frequency increases with increasing temperature change for all temperature cases. A scale coefficient ![]() ranging from 0.25 nm to 2.0 nm is used in the analysis. The nonlocal parameter effect on frequency of vibration without temperature change compared to the frequency with temperature change is more important. As the temperature change increases from 0-100 K, the nonlocal effect decreases [15]. As the environment temperature increases, there is an increase in the average distance between atoms and this causes a decrease in small scale effects [7].
ranging from 0.25 nm to 2.0 nm is used in the analysis. The nonlocal parameter effect on frequency of vibration without temperature change compared to the frequency with temperature change is more important. As the temperature change increases from 0-100 K, the nonlocal effect decreases [15]. As the environment temperature increases, there is an increase in the average distance between atoms and this causes a decrease in small scale effects [7].
The variation of non-dimensional frequency with nonlocal parameters for different boundary conditions and increasing temperature change are shown in Figure 2, Figure 3, Figure 4 and Figure 5.

Figure 2. Variation of non-dimensional frequency with nonlocal parameter for free boundary condition and ![]() K.
K.
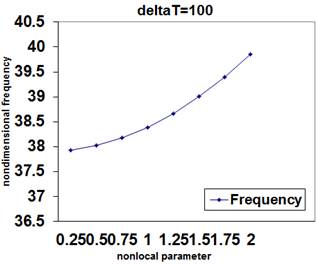
Figure 3. Variation of non-dimensional frequency with nonlocal parameter for free boundary condition and ![]() K.
K.
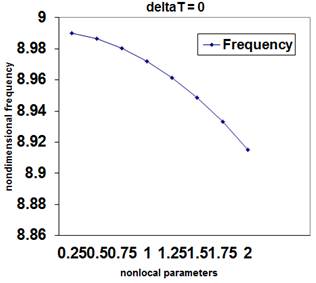
Figure 4. Variation of non-dimensional frequency with nonlocal parameter for guided boundary condition and ![]() K.
K.
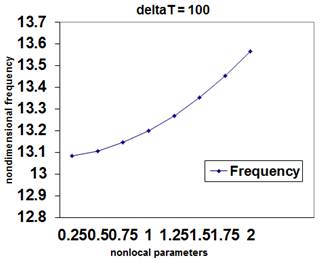
Figure 5. Variation of non-dimensional frequency with nonlocal parameter for guided boundary condition and ![]() K.
K.
Results show that the frequency of the single layered circular graphene sheet increases with the increase in the temperature change at high temperature for both free and guided boundary conditions. And there is an increase in values of frequency by increasing the nonlocal parameter.
Relationships between non-dimensional frequency versus temperature change for different boundary condition and low and high temperature cases demonstrated that the non-dimensional frequency increases as the change in temperature increases at higher temperature but decreases as the change in temperature increases at room or low temperature.
The variation of non-dimensional frequency with temperature change for different boundary conditions and temperature cases and varying nonlocal parameters are shown in Figures 6-13.
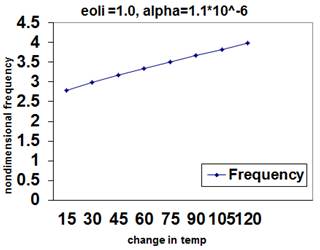
Figure 6. Variation of non-dimensional frequency with temperature change for free boundary condition in the case of high temp and nonlocal parameter as 1.
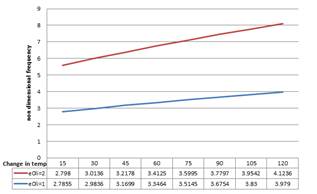
Figure 7. Variation of non-dimensional frequency with temperature change and varying nonlocal parameters for free boundary condition in the case of high temp.
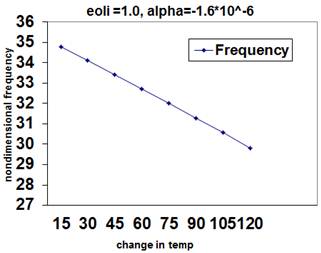
Figure 8. Variation of non-dimensional frequency with temperature change for free boundary condition in the case of room temp and nonlocal parameter as 1.
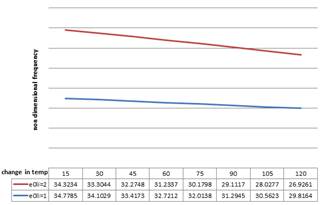
Figure 9. Variation of non-dimensional frequency with temperature change and varying nonlocal parameters for free boundary condition in the case of room temp.
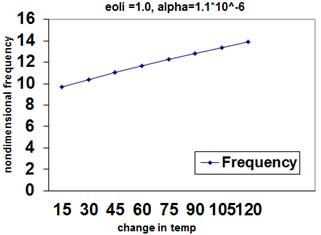
Figure 10. Variation of non-dimensional frequency with temperature change for guided boundary condition in the case of high temp and nonlocal parameter as 1.
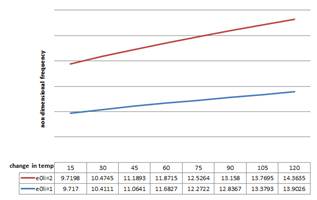
Figure 11. Variation of non-dimensional frequency with temperature change and varying nonlocal parameters for guided boundary condition in the case of high temp.
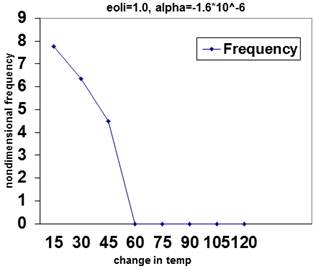
Figure 12. Variation of non-dimensional frequency with temperature change for guided boundary condition in the case of high temp and nonlocal parameter as 1.
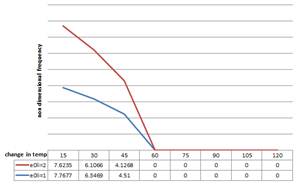
Figure 13. Variation of non-dimensional frequency with temperature change and varying nonlocal parameters for guided boundary condition in the case of room temp.
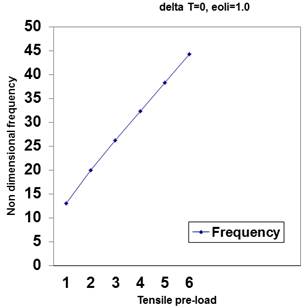
Figure 14. Variation of non-dimensional frequency with different non-dimensional tensile pre-stressed load.

Figure 15. Variation of non-dimensional frequency with different non-dimensional compressive pre-stressed load.
The study of the variation of non-dimensional frequency with in-plane and pre-stressed loads considers the first mode number and the scale coefficient as 1 nm. The in-plane loads are considered as ![]() =1, 2, 3, 4, 5, 6 for tensile pre-stressed case and
=1, 2, 3, 4, 5, 6 for tensile pre-stressed case and ![]() =l, 3, 5, 6, 7, 8, 9 and 10 for compressive pre-stressed cases. It is seen that non-dimensional frequency increases linearly with increase of tensile pre-stressed load. On the other hand the natural frequency is 0 for the maximum compressive load and it increases with the in-plane compressive pre-stressed load decreasing. The variation of non-dimensional frequency with various tensile and compressive pre-stressed loads is shown in Figure 14 and Figure 15. Table 1 illustrates the comparison of non-dimensional natural frequency of circular and square nanoplate with simply supported boundary condition.
=l, 3, 5, 6, 7, 8, 9 and 10 for compressive pre-stressed cases. It is seen that non-dimensional frequency increases linearly with increase of tensile pre-stressed load. On the other hand the natural frequency is 0 for the maximum compressive load and it increases with the in-plane compressive pre-stressed load decreasing. The variation of non-dimensional frequency with various tensile and compressive pre-stressed loads is shown in Figure 14 and Figure 15. Table 1 illustrates the comparison of non-dimensional natural frequency of circular and square nanoplate with simply supported boundary condition.
5. Conclusion
This study illustrates the significance of small scale effects and temperature change on the vibration behavior of single layered graphene sheets under in-plane pre-stressed load via nonlocal plate model theory and newton-raphson method of numerical solving. It also obtains the closed form solution for the free vibration of circular nanoplates. Results of circular graphene sheets with free and guided boundary conditions are presented.
References
- Bekir Akgöz and Ömer Civalek, Free vibration analysis for single-layered graphene sheets in an elastic matrix via modified couple stress theory, Materials and Design 42, 164-171 (2012).
- Bekir Akgöz and Ömer Civalek, Modeling and analysis of micro-sized plates resting on elastic medium using the modified couple stress theory, Meccanica 48, 863-873 (2013).
- R. Ansari, S.Sahmani and B.Arash, Nonlocal plate model for free vibrations of single-layered graphene sheets. Physics Letters A 375, 53-62 (2010).
- H.Babaei and A.R.Shahidi, Small-scale effects on the buckling of quadrilateral nanoplates based on nonlocal elasticity theory using the Galerkin method, Archive Applied Mechanic 81, 1051-1062 (2010).
- T.Murmu and S.C.Pradhan, Vibration analysis of nano-single-layered graphene sheets embedded in elastic medium based on nonlocal elasticity theory, Journal of Applied Physics. 105(6), 064319-064319-8 (2009).
- Liao-Liang Ke, Yue-Sheng Wang and Zheng-Dao Wang, Thermal effect on free vibration and buckling of size-dependent microbeams, Physica E 43, 1387-1393 (2011).
- M. Mohammadi, A. Farajpour, M. Goodarzi and F. Dinari, Thermo-mechanical vibration analysis of annular and circular graphene sheet embedded in an elastic medium, Latin American Journal of Solids and Structures 11, 659-682 (2014).
- S.C. Pradhan and J.K. Phadikar, Nonlocal elasticity theory for vibration of nanoplates, Journal of Sound and Vibration 325, 206-223 (2009).
- M. Mohammadi, M. Ghayour and A. Farajpour, Free transverse vibration analysis of circular and annular graphene sheets with various boundary conditions using the nonlocal continuum plate model, Composites: Part B 45, 32-42 (2013).
- S.C.Pradhan and T.Murmu, Small scale effect on the buckling of single-layered graphene sheets under biaxial compression via nonlocal continuum mechanics, Computational Materials Science 47, 268-274 (2009).
- L.B.Rao and C.K.Rao, Vibrations of circular plates with guided edge and resting on elastic foundation, Journal of Solid Mechanics 4(3), 307-312 (2012).
- H. Heireche, A. Tounsi, A. Benzair and M. Maachou, Sound wave propagation in single-walled carbon nanotubes using nonlocal elasticity, Physica E: Low Dimensional Systems and Nanostructures 40(8) 2791-2799 (2008).
- Haw-Long Lee and Win-Jin Chang, Closed-Form Solution for Critical Buckling Temperature of a Single-Walled Carbon Nanotube, Physica E: Low Dimensional Systems and Nanostructures 41(8) 1492-1494 (2009).
- Y.Q. Zhang, X. Liu and G.R. Liu, Thermal effect on transverse vibrations of double-walled carbon nanotubes, Nanotechnology 18(44),445701(2007).
- MATLAB User Manual Version 7.14, Mathworks (2012).



