Investment Models with Uniform Debt Repayment and Their Application
P. N. Brusov1, *, T. V. Filatova1, N. P. Orekhova2, 3, I. K. Shevchenko3, A. Y. Arkhipov3, V. L. Kulik1
1Financial University under the Government of Russian Federation, Moscow, Russia
2Research Consortium of Universities of the South of Russia, Rostov-on-Don, Russia
3South Federal University, Rostov-on-Don, Russia
Abstract
In this paper, we describe new investment models with uniform debt repayment during the life of the project, quite adequately describing real investment projects. Within these models it is possible, in particular, to analyze the dependence of effectiveness of investment projects on debt financing and taxation. We will work within developed by Brusov-Filatova-Orekhova modern theory of capital cost and capital structure as well as within a perpetuity limit.
Keywords
Debt Financing, Investment Projects with Uniform Debt Repayment, Effectiveness of Investment Project, Brusov-Filatova-Orekhova (BFO) Theory
Received: April 7, 2015
Accepted: April 24, 2015
Published online: May 27, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. The Initial Assumptions
Previously we have established investment models with debt repayment at the end of the project, well-proven in the analysis of real investment projects.
In practice, however, a scheme of uniform debt repayment during the life of the project is a more extended, to review of which this paper is devoted.
As in case of debt repayment at the end of the project the effectiveness of the investment project is considered from two perspectives: the owners of equity and debt as well as the equity holders only. In the first case, the interest and duty paid by owners of equity (negative flows), returned to the project because they are exactly equal to the flow (positive), obtained by owners of debt capital. The only effect of leverage in this case – the effect of the tax shield generated from the tax relief: interest on the loan are entirely included into the net cost and, thus, reduces the taxable base. For each of these cases, NPV is calculated in two ways: with the division of credit and investment flows (and thus discounting the payments at two different rates) and without such a division (in this case, both flows are discounted at the same rate as which, obviously, WACC can be chosen). For each of the four situations two cases are considered: 1) a constant value of equity S; 2) a constant value of the total invested capital I = S + D (D is value of debt funds).
The main debt repayment occurs evenly (by equal parts) at the end of each period, and the remaining debt at the end of the each period is an arithmetic progression with the difference ![]()
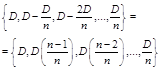 (1)
(1)
Interest constitute a sequence
![]() (2)
(2)
In the case of consideration from the point of view of equity owners and debt owners the after tax flow of capital for each period is equal to
![]() , (3)
, (3)
where
![]() , (4)
, (4)
and investment at time moment ![]() are equal to –I = –S – D. Here NOI – net operating income (before tax).
are equal to –I = –S – D. Here NOI – net operating income (before tax).
In the second case (from the point of view of equity owners only) investment at the initial moment ![]() are equal to –S, and the flow of capital for the period (apart from tax shields
are equal to –S, and the flow of capital for the period (apart from tax shields ![]() it includes payment of interest on the loan
it includes payment of interest on the loan ![]() ) is equal to
) is equal to
![]() . (5)
. (5)
We suppose that the interest on the loan, as well as the loans itself are paid in tranches ![]() and
and ![]() consequently during the all i-th periods. We cite in table 1 the sequence of debt values and credit values.
consequently during the all i-th periods. We cite in table 1 the sequence of debt values and credit values.
Table 1. Debt values and credit values.
| Period number | 1 | 2 | 3 | n |
| debt | D |
|
|
|
| interest |
|
|
|
|
As in case of debt repayment at the end of the project we will consider two different ways of discounting:
1. Operating and financial flows are not separated and both are discounted at the general rate (as which, obviously, can be selected the weighted average cost of capital, WACC). The Modigliani–Miller formula (Мodigliani and Мiller (1963)) for WACC for perpetuity projects will be used and for projects of finite duration Brusov-Filatova-Orekhova formula will be used (Brusov & Filatova, 2011; Brusov, Filatova, Eskindarov, et al., 2011; Brusov, Filatova, Orehova, et al., 2011; Brusov, Filatova, & Orekhova, 2013b; Filatova, Orehova, & Brusova, 2008; P.N. Brusov, T.V. Filatova and N.P. Orekhova (2014)).
2. Operating and financial flows are separated and are discounted at different rates: the operating flow at the rate equal to the equity cost ![]() , depending on leverage, and credit flow –at the rate equal to the debt cost
, depending on leverage, and credit flow –at the rate equal to the debt cost ![]() , which until fairly large values of leverage remains constant and starts to grow only at high values of leverage L, when there is a danger of bankruptcy.
, which until fairly large values of leverage remains constant and starts to grow only at high values of leverage L, when there is a danger of bankruptcy.
Note once again that, loan capital is the least risky, because interest on credit is paid after tax in the first place. Therefore, and the cost of credit will always be less than the equity cost, whether of ordinary or of preference shares ![]() . Here
. Here ![]() – equity cost of ordinary or of preference shares consequently.
– equity cost of ordinary or of preference shares consequently.
One can show that the present value of interest can be calculated by using the following formula, which we have been able to derive
 (6)
(6)
We will use this formula in the further calculations.
2. The Effectiveness of the Investment Project from the Perspective of the Equity Holders Only
2.1. With the Division of Credit and Investment Flows
To obtain an expression for NPV discounted flows values for one period, given formulas (3), or (5) must be summed, using the obtained by us formula (6), in which ![]() , where i is the discount rate. Its accurate assessment is one of the most important advantages of BFO theory (Brusov-Filatova-Orekhova) (Brusov & Filatova, 2011; Brusov, Filatova, Eskindarov, et al., 2011; Brusov, Filatova, Orehova, et al., 2011; Brusov, Filatova, & Orekhova, 2013b; Filatova, Orehova, & Brusova, 2008; P.N. Brusov, T.V. Filatova and N.P. Orekhova (2014)) over its perpetuity limit - Modigliani–Miller theory (Modigliani & Miller, 1958, 1963, 1966).
, where i is the discount rate. Its accurate assessment is one of the most important advantages of BFO theory (Brusov-Filatova-Orekhova) (Brusov & Filatova, 2011; Brusov, Filatova, Eskindarov, et al., 2011; Brusov, Filatova, Orehova, et al., 2011; Brusov, Filatova, & Orekhova, 2013b; Filatova, Orehova, & Brusova, 2008; P.N. Brusov, T.V. Filatova and N.P. Orekhova (2014)) over its perpetuity limit - Modigliani–Miller theory (Modigliani & Miller, 1958, 1963, 1966).
In this case, the expression for NPV has a view
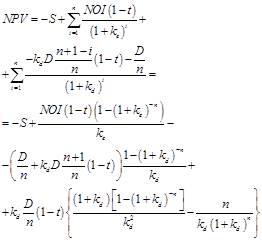 (7)
(7)
In perpetuity limit (let us call it Modigliani–Miller limit) one has
![]() (8)
(8)
2.2. Without Flows Separation
In this case operating and financial flows are not separated and are discounted at the general rate (as which, obviously, the weighted average cost of capital, WACC can be selected). The main debt repayment, which occurs evenly (by equal parts) at the end of each period, can be discounted either at the same rate WACC, or that is more logical, at the debt cost rate ![]() . Now we choose a uniform rate and the first option.
. Now we choose a uniform rate and the first option.
We still consider the effectiveness of the investment project from the perspective of the equity holders only.
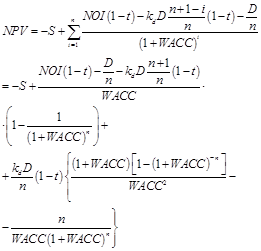 (9)
(9)
In perpetuity limit (Modigliani–Miller limit) (turning to the limit ![]() in the relevant equations) we have
in the relevant equations) we have
![]() (10)
(10)
3. The Effectiveness of the Investment Project from the Perspective of the Owners of Equity and Debt Projects of Arbitrary (Finite) Duration
3.1. With Flows Separation
In case of consideration from the perspective of the owners of equity and debt
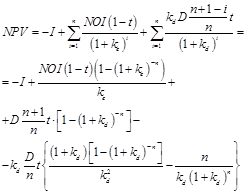 (11)
(11)
In perpetuity limit (Modigliani–Miller limit) (turning to the limit ![]() in the relevant equations) we have
in the relevant equations) we have
![]() (12)
(12)
3.2. Without Flows Separation
We still consider the effectiveness of the investment project from the perspective of the owners of equity and debt.
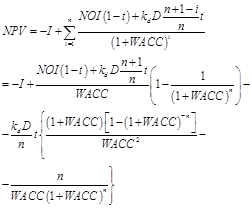 (13)
(13)
In perpetuity limit (Modigliani–Miller limit) (turning to the limit ![]() in the relevant equations) we have
in the relevant equations) we have
![]() (14)
(14)
4. Example of the Application of the Derived Formulas
As an example of application of the obtained formulas let's take a look at the dependence of the NPV of project on the leverage level at three values of the tax on profit rates in case of consideration from the perspective of the equity holders only without flows separation on operating and finance ones. We use formula (10) and the next parameters values ![]() Making the calculations in Excel, we get the data, which are shown in figure 1.
Making the calculations in Excel, we get the data, which are shown in figure 1.

Fig. 1. Dependence of NPV of the project on the leverage level at three values of the tax on profit rates.
![]() .
.
From the calculations, and figure 1 one can make the following conclusions:
1. The growth of the tax on profit rates NPV of the project decreases and it is possible to assess for how many per cent, with growth of tax on profit rate, for example, by 1 %.
It should be noted that the possibility of such evaluations is unique.
2. Effects of taxation on the NPV significantly depend on the leverage level:
with its increasing the impact of changing of tax on profit rates is greatly reduced. This is valid for increasing of the tax on profit rate, and its reduction.
3. With the existing (20 %) and higher (25 %) tax on profit rates there is an optimum in NPV dependence on leverage. Investors should take into account the invested capital structure: in this case, they may, without special effort (only changing this structure), obtain (sometimes very substantial) gains in NPV
5. Conclusions
New investment models with uniform debt repayment during the life of the project, quite adequately describing real investment projects are described. Within these models it is possible, in particular, to analyze the dependence of effectiveness of investment projects on debt financing and taxation. We will work within developed by Brusov-Filatova-Orekhova modern theory of capital cost and capital structure as well as within a perpetuity limit.
As in case of debt repayment at the end of the project the effectiveness of the investment project is considered from two perspectives: the owners of equity and debt as well as the equity holders only. For each of these cases, NPV is calculated in two ways: with the division of credit and investment flows (and thus discounting the payments at two different rates) and without such a division (in this case, both flows are discounted at the same rate as which, obviously, WACC can be chosen). For each of the four situations two cases are considered: 1) a constant value of equity S; 2) a constant value of the total invested capital I = S + D (D is value of debt funds).
As an example of application of the obtained formulas the dependence of the NPV of project on the leverage level at three values of the tax on profit rates has been investigated in case of consideration from the perspective of the equity holders only without flows separation on operating and finance ones. It has been shown that effects of taxation on the NPV significantly depends on the leverage level: with its increasing the impact of changing of tax on profit rates is greatly reduced. This is valid for increasing of the tax on profit rate, and its reduction. Model allows to investigate the dependence of effectiveness of the investment project on leverage level, on the tax on profit rate, on credit rate, on equity cost etc.
References
- Brusov P, Filatova T, Orehova N, Eskindarov M (2015a), Modern corporate finance, investments and taxation, Springer International Publishing, Switzerland, 373 p.
- Brusov, P. N., & Filatova, T. V. (2011). From Modigliani–Miller to general theory of capital cost and capital structure of the company. Finance and Credit, 435, 2–8.
- Brusov, P., Filatova, T., Eskindarov, M., Orehova, N., Brusov, P., & Brusova, A. (2011). Influence of debt financing on the effectiveness of the finite duration investment project. Applied Financial Economics, 22, 1043–1052.
- Brusov, P., Filatova, T., Orehova, N., & Brusova, N. (2011). Weighted average cost of capital in the theory of Modigliani–Miller, modified for a finite life-time company. Applied Financial Economics, 21, 815–824.http://dx.doi.org/10.1080/09603107.2010.537635.
- Brusov, P., Filatova, T., Orehova, N., Brusov, P. P., & Brusova, N. (2011a). Influence of debt financing on the effectiveness of the investment project within Modigliani–Miller theory. Research Journal of Economics, Business and ICT, 2, 11–15.
- Brusov, P., Filatova, T., Orehova, N., Brusov, P. P., & Brusova, N. (2011b). From Modigliani–Miller to general theory of capital cost and capital structure of the company. Research Journal of Economics, Business and ICT, 2, 16–21.
- Brusov, P. N., Filatova, T. V., & Orekhova, N. P. (2013a). Absence of an optimal capital structure in the famous tradeoff theory! Journal of Reviews on Global Economics, 2, 94–116.
- Brusov, P. N., Filatova, T. B., & Orekhova, N. P. (2013b). Modern corporate finance and investment (517 pp.). Moscow: Knorus.
- Filatova, T. V., Orehova, N. P., & Brusova, A. P. (2008). Weighted average cost of capital in the theory of Modigliani–Miller, modified for a finite life-time company. Bulletin of the FU, 48, 68–77.
- Modigliani, F., & Miller, M. (1958). The cost of capital, corporate finance and the theory of investment. American Economic Review, 48, 261–297.
- Modigliani, F., & Miller, M. (1963). Corporate income taxes and the cost of capital: A correction. American Economic Review, 53, 147–175.
- Modigliani, F., & Miller, M. (1966). Some estimates of the cost of capital to the electric utility industry 1954–1957. American Economic Review, 56, 333–391.
- P.N. Brusov, T.V. Filatova and N.P. Orekhova (2014), Mechanism of formation of the company optimal capital structure, different from suggested by trade off theory// Cogent Economics & Finance, v.2, p. 1-13; http://dx.doi.org/10.1080/23322039.2014.946150.



