Thermodynamic Performance Analysis of Different Organic Rankine Cycles to Generate Power from Renewable Energy Resources
Abtin Ataei1, 2, *, Farid Safari1, Jun-Ki Choi2
1Department of Energy Engineering, Graduate School of the Environment and Energy, Science and Research Branch, Islamic Azad University, Tehran, Iran
2Mechanical and Aerospace Engineering / Renewable and Clean Energy, University of Dayton, Dayton, Ohio, USA
Abstract
Organic Rankine cycles (ORCs), are promising technologies for generating power from low and medium grade of heat resources such as geothermal fluids or the synthetic gas from biomass gasification, that have received lots of attention during past twenty years. In this study, thermodynamic evaluations were used based on the first and second laws of thermodynamics to compare different organic fluids and different configuration of Rankine cycles. Energy and Exergy analysis of different configurations of ORCs including basic ORC, basic ORC with Internal Heat Exchanger (IHE), Regenerative ORC and Regenerative ORC with IHE for four dry organic fluids including R113, RC318, iso-pentane and n-hexane, in various ambient temperatures, were simulated using Engineering Equation Solver (EES). In addition, environmental performances were evaluated using the sustainability index method which was resulted from Exergy analysis. The results indicated that the Regenerative ORC with IHE has the best thermodynamic performance with thermal and second law efficiency of 0.217 and 0.642, respectively. It was concluded that the n-hexane which has the highest boiling point and critical temperature is the most efficient working fluid for the cycle. The results indicated that a reduction in ambient temperature causes an increment in both thermal and second law efficiencies and makes the system more sustainable due to an increment in the sustainability index.
Keywords
Exergy Destruction, Regeneration, Heat Exchanger, Sustainability Index
Received: June 8, 2015
Accepted: June 18, 2015
Published online: July8, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
Renewable energy is one of the key options for approaching energy security and sustainable development in modern era. These kinds of energy resources such as solar, biomass, wind, geothermal and tidal energy have a great potential for generating power and because of their reliability and availability, researchers paid lots of attention to them, in the last decades. One of them is geothermal energy that is always available and comes from earth's crust. The Major world's geothermal energy applications are a 12GW electricity production and a direct use for heating of 23 GW in 2013 [1].
Organic Rankine cycles are promising technologies for development and conversion of low and medium grade heat resources into power. For three decades many researchers have worked on this subject and have used scientific fundamentals for more efficient and suitable conversion of these kinds of energy resources into power in power plants.
ORCs work with Traditional Clausius-Rankine principles but use organic dry fluids instead of water [2]. That makes them able to generate power and remain superheat after expansion in turbine in low and medium temperatures. The process of making electricity from renewable energy resource should be economically viable. Some new methods have been proposed for overcoming this challenge such as a value-based planning method for combined cooling, heating and power (CCHP) placement based on the energy hub concepts or Feed-In-Tariff (FIT) policies which are regarded as one of the efficient strategies in stimulating renewable energy development [3,4].
In case of ORC's, an appropriate fluid should be used to obtain the maximum thermal efficiency and minimum exergy destruction rate in the process. As seen in Fig. 1, The slope of saturation curve in the T-S diagram of the cycle depends on type of the fluid which is deployed. Dry fluid has a positive slope; wet fluid has a negative slope and isentropic fluid has almost infinite slope. The dry fluids with lower critical points are vaporized in lower temperatures and not condensed after passing the turbine because of their overhanging coexistence curve in T-S diagram and this, results a better thermal efficiency [5].
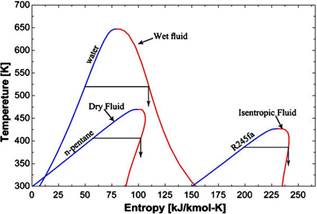
Fig. 1. T-S diagram for wet, dry and isentropic fluids [2].
The literature shows extensive analyses and comparisons among different thermodynamic cycles and working fluids for ORCs. Hung [6], investigated the thermodynamic performance of a simple ORC by using different working fluids. Those results indicated that, among those fluids, p-Xylene showed the highest efficiency while benzene showed the lowest. Chen et al [3], presented a comparative study of an ORC and trans-critical CO2 cycles to convert low grade waste heat into power. Saleh et al [2], presented a thermodynamic performance of 31 working fluids for ORC using BACKONE equation of state. Those results showed that, the highest efficiency are obtained for the highest boiling point substance in a process with IHE. Mago et al. [7], presented the second law analysis for ORC with R134a, R113, R245fa, R123, iso-butane, and propane. Those results demonstrated that the ORC using R113 works with the maximum efficiency among other working fluids in a temperature below 430 K. Yari, studied the exergy analysis for different organic Rankine cycles with R227EA, RC318, R236FA, iso-butane, R600A, R245fa, HFE7000, R123, R113 as working fluids. The results indicated that a fluid with a higher boiling point showed a better performance in the cycle. It was shown that using IHE and regeneration may affect the performance of the system [8]. Cammarata et al. [9], presented a numerical simulation of ORC which was powered by geothermal energy resource with iso-butane and iso-pentane as working fluids. It was shown that a reduction in temperature of condenser increased the thermal efficiency. It was also seen that iso-butene works better for conversion of geothermal energy into power due to its higher boiling point.
However most of the comparisons have been conducted under certain predefined temperatures, the effect of the ambient temperature have not been considered. In addition, the environmental sustainability has not been studied for ORC's alongside other thermodynamic indicators yet. In this article, various aspects of the cycle's thermodynamic performance including energy, exergy and sustainability analysis in different ambient temperatures were studied together and the most efficient working fluid was chosen with a comparison between four different working fluids with different physical properties.
2. System Description
ORCs work like steam Rankine cycles but with an organic fluid instead of water. As shown in Fig. 2, an ideal basic Rankine cycle has 4 steps including an isentropic compression in pump, evaporation at constant pressure in evaporator, isentropic expansion in turbine and constant pressure phase change of the expanded steam in condenser with air cooling stream. These configurations of ORC are shown in Figs. 2 to 5. Figs. 2, 3, 4 and 5 show basic ORC, basic ORC with IHE, regenerative ORC and regenerative ORC with IHE, respectively. In regenerative ORC with IHE, the working fluid is preheated before the evaporator and pre-cooled before the condenser in IHE. Then, it is heated more in a closed feed organic fluid heater by extracted vapor from the turbine. In this study, these four configurations were simulated with some feasible operational parameters. Four different dry organic fluids including n-hexane, iso-pentane, R113 and RC318 were used for this simulation.
3. Thermodynamic Analysis
In this part, energy and exergy analyses via thermodynamic equations for each component based on first and second law of thermodynamics are presented. The assumptions for the system were as follows;
• Systems simulated under steady state conditions.
• Efficiencies of the pump and turbine were assumed as isentropic.
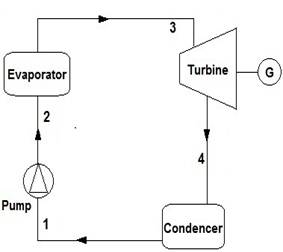
Fig. 2. Schematic for basic ORC.
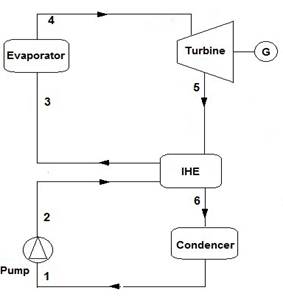
Fig. 3. Schematic for basic ORC with IHE.
The two main equations were used for analysis in this study, are the first and second laws of thermodynamics that can be expressed respectively as follows[10];
![]() (1)
(1)
![]() (2)
(2)
These two are the main principles for energy analysis of the cycles and with the assumptions for a steady state condition;
![]() (3)
(3)
For exergy analysis, rate of exergy loss can be written as follow [10];
![]() (4)
(4)
Where the subscript k represents the heat transfer location. Equations of regenerative ORC with IHE for each component are expressed further. For other configurations these equations can be simplified.

Fig. 4. Schematic for regenerative ORC.
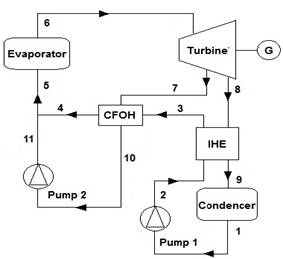
Fig. 5. Schematic for regenerative ORC with IHE.
3.1. Component Analysis
3.1.1. Pump
Pumps derive ORC and their power can be obtained as follows [11];
![]() (5)
(5)
Where ![]() is the isentropic power of the pump. Note that numerical subscripts specify the conditions in Fig. 5. For example,
is the isentropic power of the pump. Note that numerical subscripts specify the conditions in Fig. 5. For example, ![]() and
and ![]() are the enthalpies of the working fluid at inlet and outlet of the pump, respectively. Furthermore,
are the enthalpies of the working fluid at inlet and outlet of the pump, respectively. Furthermore, ![]() is the isentropic efficiency and
is the isentropic efficiency and![]() is the fraction of flow rate that extracted from the turbine. Actual specific enthalpy at the outlet is as follow;
is the fraction of flow rate that extracted from the turbine. Actual specific enthalpy at the outlet is as follow;
![]() (6)
(6)
The exergy destruction rate for the pump can be written as follow;
![]() (7)
(7)
Where ![]() and
and ![]() are the specific entropies of the working fluid at outlet and inlet of the pump in an actual condition. Similarly to pump1, those equations can be written for pump 2 as follows [10];
are the specific entropies of the working fluid at outlet and inlet of the pump in an actual condition. Similarly to pump1, those equations can be written for pump 2 as follows [10];
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
3.1.2. Evaporator
The evaporator is where the heat transfer in constant pressure occurs. This component heats the working fluid from the pump outlet to turbine inlet condition which can be saturated or superheated. The evaporator's heat transfer can be written as follow;
![]() (11)
(11)
The exergy destruction in the evaporator can also be written as;
![]() ] (12)
] (12)
Where, ![]() is the high temperature of heat source. This temperature is equal to
is the high temperature of heat source. This temperature is equal to ![]() +
+![]() so that
so that ![]() is 15 degrees of Kelvin and specified via mago et al. [7]
is 15 degrees of Kelvin and specified via mago et al. [7]
3.1.3. Turbine
Turbine generates mechanical power by expansion of the saturated or superheated working fluid and depressurizes it by turbine blades. Turbine's power, actual outlet, specific enthalpy and exergy destruction rate are expressed, respectively as follows;
![]() =
=![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
3.1.4. Condenser
The working fluid goes through a constant pressure condensation in the condenser and becomes saturated liquid for pumping condition. This process gives latent heat to the environment that can be expressed as follow;
![]() (17)
(17)
Furthermore, exergy loss for the condenser can be determined as;
![]() ] (18)
] (18)
Where ![]() is the low temperature of heat source. This temperature is equal to
is the low temperature of heat source. This temperature is equal to ![]() so that
so that ![]() is 15 degrees of Kelvin and specified via mago et al. [7]
is 15 degrees of Kelvin and specified via mago et al. [7]
3.1.5. Internal Heat Exchanger
With Ideal assumption, and neglecting pressure drop, the process in IHE would be a constant pressure heat transfer. In IHE, compressed liquid from pump gives heat to expanded organic vapor coming from turbine's outlet. Heat transfer rate in IHE can be described as
![]() (19)
(19)
Also, the effectiveness of IHE is determined as follow;
![]() (20)
(20)
And finally, the exergy destruction rate for IHE is calculated as follow;
![]() (21)
(21)
3.1.6. Close Feed Organic Fluid Heater (CFOH)
CFOH in this study is a way to regenerate energy from the expanded steam at turbine's outlet for preheating the liquid pumped from the circulation pump without any mixing. With balancing the mass and energy, the following equation is used to calculate the mass fraction extracted from the turbine;
![]() (22)
(22)
And, the exergy destruction rate in CFOH is;
![]() (23)
(23)
3.2. Overall Cycle Analysis
3.2.1. Cycle Efficiency
Thermal efficiency is described as the quantity of the heat transferred in evaporator that converted into work in turbine and expressed as;
![]() =
=![]() (24)
(24)
3.2.2. Total Exergy Destruction Rate
Total exergy destruction rate is a parameter to determine the cycle's reversibility and its potential to convert the low or medium heat from renewable resources into useful work. The exergy destruction should be minimized in order to achieve a more sustainable system. That rate can be written for the cycle as the following equation [11];
![]() ] (25)
] (25)
3.2.3. Second Law Efficiency
The second law efficiency can be calculated by as the following equation [10];
![]() (26)
(26)
3.2.4. Sustainability Index (SI)
Sustainability index (SI) method have been deployed in this article to realize the environmental problems and the sustainability of the systems. The relation between the second low efficiency and SI is mentioned as below[12];
![]() (27)
(27)
Where Dp is the depletion factor defined by Connelly and Koshland [13] as the ratio of exergy destruction rate to the input exergy rate of the system and can be given as [14] follow;
![]() (28)
(28)
SI is in to indicate how much exergy is destroyed in the system. With these analysis, different configurations of ORC with different working fluids were simulated by engineering equation solver program (EES) and a comparison between different configurations of ORC were done. Moreover, variation of the thermal efficiency, the exergy destruction rate and second law efficiency with the turbine inlet pressure and ambient temperature, were investigated. It should be mentioned that in this investigation, the optimum pressure of the extracted flow from the turbine goes into CFOH for R113, was determined according to Wark and Richard [15] as follows;
![]() For regenerative ORC (29)
For regenerative ORC (29)
![]() For regenerative ORC with IHE (30)
For regenerative ORC with IHE (30)
Table 1 summarizes the basic assumptions and input parameters of the simulation in this work. In order to determine the performance of the system with variation of the turbine inlet pressure and ambient temperature, it is assumed that the system works at turbine inlet pressures between 0.5 and 3 Mpa, and the temperature is between 283 and 313 degrees of Kelvin to determine the optimum conditions for the cycle. The efficiencies of some different components were chosen from the literatures as shown in Table 1.
Table 1. Parameters used in this simulation.

Table 2. Properties of the dry organic fluids used in this study.
| Organic fluid | Molecular weight[g/mol] | Boiling point [k] | Tcritical [k] | [Mpa] |
| n-Hexane | 86.17 | 341.9 | 507.4 | 3.01 |
| Iso Pentane | 72.15 | 301.1 | 460.4 | 3.38 |
| R113 | 187.4 | 320.4 | 487.3 | 3.44 |
| RC318 | 200.04 | 267.2 | 388.4 | 2.78 |
Table 2, includes working fluids that were used in this study and their properties. Four different boiling points and critical conditions associated with four different working fluids, were selected to determine how these may affect the performance parameters of the cycle.
4. Results and Discussion
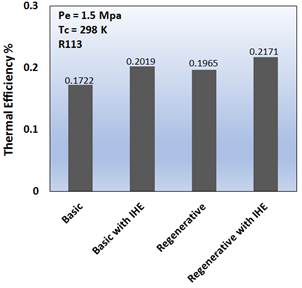
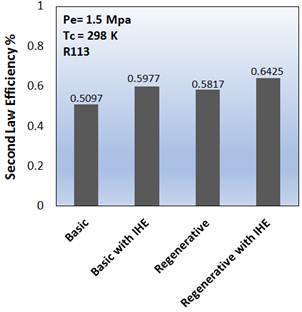
The results of this study were presented in four parts. The first part is a comparison between four configurations presented in Figs. 2 to 5 in a constant operational condition with R113 as the working fluid. These four configurations were compared in Fig. 6a and 6b from the thermal efficiency point of view, second law efficiency and exergy destruction rate, respectively. The conditions for each configuration were kept at temperature of 298 K and pressure of 1.5 Mpa. The results indicated that using internal heat exchanger causes an increment in both thermal and second law efficiency and a decrement in the exergy destruction rate due to the reduction of supplied heat of the system and the heat rejected into the environment. These two, may cause a reduction in the mean temperature difference in the evaporator and condenser and that results a lower Exergy destruction rate and higher second law efficiency. Furthermore, as seen in equation (24), the reduction in heat supply with same turbine inlet conditions occurs in higher thermal efficiencies. As seen in Fig. 6, the ORC with IHE shows a 26% increment of thermal efficiency in comparison with the basic ORC.
(a)
(b)
Fig. 6. Thermal and second-law efficiencies for different configurations of ORC.
Fig. 7 depicts a comparison between different ORC configurations from the exergy destruction rate point of view. The exergy destruction rate shows the irreversibility of the cycle and destruction of the potential for power generation from the energy resource with consideration of the environmental conditions. Fig. 7 shows the effect of regeneration and internal heat exchanger on the system so that the rate of exergy drstructed in the regenerative ORC with IHE is 25.05 kJ/kg less than that of the Basic ORC.

Fig. 7. Exergy destruction rate for different configurations of ORC.
(a)
(b)
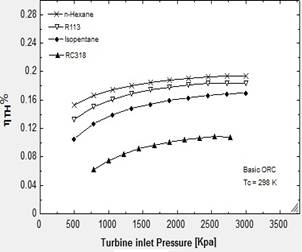
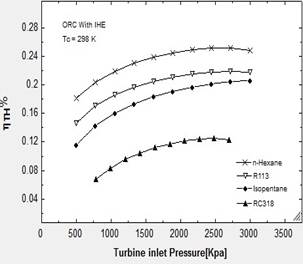
Fig. 8. Variation of thermal efficiency with turbine inlet temperature for the basic ORC and ORC with IHE working with different dry fluids.
The second part of the results is about a comparison between the different organic fluids and relations between their properties and performance. Fig. 8a and 8b show the variation of the thermal efficiency of basic ORC and basic ORC with IHE with the turbine inlet pressure, respectively. Four organic working fluids including n-hexane, iso-pentane, RC318 and R113 were considered. The results indicated an increment in the turbine inlet pressure follows with more heat supply and more network in the turbine, but the percentage of the increment in work is more than that of the heat supply. As a result, the thermal efficiency increased. This Figure also demonstrates that fluids with a higher boiling point and a critical temperature show a better performance in ORC's. Among these fluids, n-hexane has the best performance and RC318 has the worst. According to Table 2, it can be concluded that the boiling point and critical temperature of the organic working fluid have a direct relation with the system's thermal efficiency.
(a)
(b)
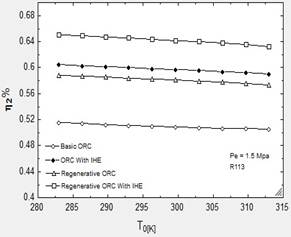
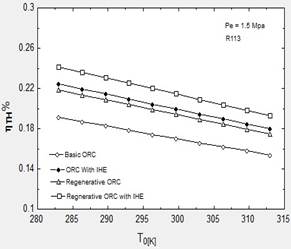
Fig. 9. Variation of thermal and second law efficiencies with the ambient temperature for different configurations of ORC.
Third part of the results is about the effect of ambient temperature on efficiencies. The results in Figs. 9a and 9b, indicate that the thermal efficiency increases with a decrement of the ambient temperature. This is because, as the ambient temperature decreases, the mean temperature difference of condenser and evaporator decreases as well but a reduction in heat rejected to the environment, is more than of the heat supplied to the cycle. Therefore, the thermal efficiency increases. It has also been shown that the second law efficiency slightly decreases with an increment of the ambient temperature.
The last part of the results is about system's sustainability which is measured by SI. Fig. 10 indicates that the lower temperatures slightly cause a better environmental performance and a higher SI for the system. Hence, with the temperatures between 283 to 313 K, SI decreases slightly from 2.42 to 2.34 and depletion factor (Dp) increases from 0.412 to 0.426.
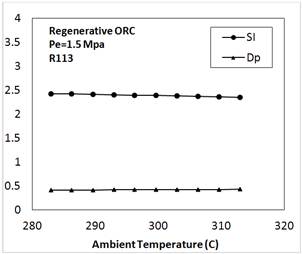
Fig. 10. Variation of SI and Dp with the ambient temperature for regenerative ORC.
5. Conclusion
This paper presented a simulation for different configurations of organic Rankine cycles powered by low grade heat resources in feasible operational conditions based on first and second law of thermodynamics to find the efficient configuration, working fluid, ambient temperature and environmental condition. A comprehensive analysis for these systems was performed for all operational indicators which have not been investigated together before. Working fluids used in this study were R113, RC318, iso-pentane and n-hexane. The main results from the simulation are summarized as follows:
• Internal heat exchanger and regeneration increase both thermal and second law efficiencies and decrease the exergy destruction rate.
• Fluids with higher boiling points and critical temperatures have higher thermal efficiencies.
• A reduction in the ambient temperature increases system's thermal efficiency.
• Cycles with IHE and Regeneration that work in lower ambient temperatures have higher Sustainability indexes.
References
- REN21. 2014. Renewables 2014 Global Status Report. (Paris:REN21Seretriat)
- Saleh, B., Koglbauer, G., Wendland, M., and Fischer, J., "working fluids for low temperature organic Rankine cycles," Energy, Vol. 32, pp.1210-1221, 2007.
- A. Sheikhi, A. M. Ranjbar, H.Oraee, "Financial analysis and optimal size and operation for a multicarrier energy system,"Energy and Buildings,Vol.48, pp.71-78, May 2012.
- S. Bahrami, A. Sheikhi, "An Optimal Feed-In-Tariff Policy for Renewable Energies UsingA Markov Model,"American Journal of Renewable and Sustainable Energy, Vol. 1, No. 1, pp.1-8, May 2015.
- H. Chen, D. Goswami, E. K. Stefanakos, "A review of thermodynamic cycles and working fluids for the conversion of low-grade heat," Renewable and Sustainable Energy Reviews. Vol.14, pp.3059–3067, 2010.
- T. C. Hung, "Waste heat recovery of organic Rankine cycle using dry fluids," Energy Conversion and Management, Vol.36, pp.539-553, 2001.
- P. J. Mago, L. M. C. harma, C. C. Somayaji, "Performance analysis of different working fluids for use in organic Rankine cycles," Proc. Imech E., Vol. 221 Part A: journal of Power and Energy, pp.225-264, 2007.
- M. Yari, "Performance analysis of the different Organic Rankine Cycles (ORCs) using Dry Fluids. International Journal of Exergy,Vol.6, No.3, pp.323-342, 2009.
- G. Cammarata, L. Cammarata, G. Petrone, "Thermodynamic analysis of ORC for energy production from geothermal resource," 68th Conference of the Italian Thermal Machines Engineering Association, 2003.
- Y. A. Chengel, and M. A. Boles, "Thermodynamics An Engineering Approach," 6th ed., McGraw-Hill Inc., New York, 2007.
- M.J. Moran, H. N. Shapiro, "Fundamentals of Engineering Thermodynamics, 5th ed., John Wiley and Sons, New York, 2006.
- M. A. Rosen, I. Dincer, M. Kanoglu, "Role of exergy in increasing efficiency and sustainability and reducing environmental impact," Energy Policy, vol. 36, pp. 128-137, 2008.
- L. Connelly, C. P. Koshland, "Two aspects of consumption: using an exergy-based measure of degradation to advance the theory and implementation of industrial ecology," Resources, Conservation and Recycling, Vol.19, pp. 199-217, 1997.
- Y. Kalinci, A. Hepbasli, I.Dincer, "Performance assessment of hydrogen production from a solar-assisted biomass gasification system," International Journal of Hydrogen Energy, Vol. 38, pp. 6120-6129, 2013.
- K. Wark, D. E. Richard, "Thermodynamics," 6th edition, McGraw-Hill INC., New York, 1999.
- Drescher, U., Bruggemann, D, "Fluid selection for the organic Rankine cycle in biomass power and heat plants," Applied Thermal Engineering, Vol.27, pp.223-228, 2007.
- H. D. M. Hettiarachchia, M. Golubovika, W. M. Woreka,Y. Ikegami, "Optimum design criteria for an organic Rankine cycle using low-temperature geothermal heat sources," Energy, Vol.32, pp.1698-1706, 2007.
- A. C. Mcmahan, "Design and optimization of organic Rankine cycle solar thermal power plants," MS Thesis, University of Wisconsin at Madison, 2006.



