LBM Simulation of Porous Block Effects on Force Convection in a Channel
Mojtaba Aghajani Delavar*, Mehran Valizadeh
Faculty of Mechanical Engineering, Babol Noshirvani University of Technology, Babol, Iran
Abstract
In this paper heat transfer in a channel with a heat generating porous block has been investigated numerically by using Lattice Boltzmann Method (LBM). The effects of block porosity, height and effective thermal conductivity as well as flow Reynolds number over flow pattern and heat transfer were studied. Results indicate that with rise in block's height (while block's surface remains constant) fluid's temperature would increase. As Reynolds number increases, maximum temperature in block would decline due to reduction in heat transfer between heat source in porous block and fluid. Averaged temperature would increase as block's height grows. Moreover, higher porosity would enhance fluid's temperature because of less heat transfer with adjacent cold walls. Additionally, it was seen that, effects of porosity and block's height on thermal field in porous block are more sensible in contrast with concerned Reynolds numbers.
Keywords
Lattice Boltzmann Method, Heat Generating, Porous Block
Received:May 13, 2015
Accepted: May 25, 2015
Published online: June 28, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
The fundamentals of heat transfer and fluid flow in porous media have been considered widely such as [1-4] because of its importance in many engineering applications, such as: petroleum processing, geothermal energy extraction, catalytic and chemical particle beds, heat transfer enhancement, solid matrix or micro-porous heat exchangers, direct contact heat exchangers, heat pipes, electronic cooling, drying processes, and many others.
Zhang and Zhao [5] numerically investigated the fluid flow over a backward-facing step with a porous block insert directly behind it in order to explore the use of porous inserts for heat transfer enhancement in recirculating flow. Their results showed that the use of even relatively lower thermal conductive porous insert would improve heat transfer performance strikingly. The compact heat sink simulations in forced convection flow with side-bypass effects were carried out by Jeng [6]. He used the Brinkman–Forchheimer model for fluid flow and two-equation model for heat transfer. Li et al. [7] numerically investigated the fluid flow and heat transfer characteristics in a channel with staggered porous blocks. The Brinkman-Forchheimer equation was used to model the fluid flow in the porous regions. They illustrated that an increase in the thermal conductivity ratio between the porous blocks and the fluid makes significant enhancement of heat transfer at the porous blocks.
Alazmi and Vafai [8] analyzed different types of interfacial conditions between a porous medium and a fluid layer. They investigated the differences between five primary categories of interface for the fluid flow at the interface region and four categories of interface conditions for the heat transfer at the interface region.
Khanafer and Chamkha [9] investigated numerically the mixed convection in a horizontal annulus filled with a uniform fluid-saturated porous medium in the presence of internal heat generation. The effects of the Rayleigh number, the Darcy number, the annulus gap, and the Richardson number on the flow and heat transfer characteristics were considered.
Narasimhan and Reddy [10] investigated the thermal management of heat generating electronics using the Bi-Disperse Porous Medium (BDPM). The BDPM channel comprises heat generating micro-porous square blocks separated by macro-pore gaps.
Jeng et al [11] presented a semi-empirical model associated with an improved single blow method for exploring the heat transfer behavior in porous channels. They study the heat transfer paths and mechanisms in such a complicated porous channel.
The lattice Boltzmann method (LBM) is a powerful numerical technique based on kinetic theory for simulation of fluid flows and modeling the physics in fluids [12-16]. In comparison with the conventional CFD methods, the advantages of LBM include: simple calculation procedure, simple and efficient implementation for parallel computation, easy and robust handling of complex geometries and so forth. In the last years lattice kinetic theory, and most notably the lattice Boltzmann method has evolved as a significant success alternative numerical approach for the solution of a large class of problems ( [12,17,22])
Seta et al. [23,24] used thermal lattice Boltzmann method to study natural convection and other thermal problems in porous media. They confirm the reliability and the computational efficiency of the lattice Boltzmann method in simulating natural convection in porous media at the representative elementary volume scale. The influence of porous media was considered by introducing the porosity to the equilibrium distribution function and by adding a force term to the evolution equation. Mantle et al. [25] investigate experimentally and numerically the flow of a Newtonian liquid through a dual porosity structure. The numerical simulations have been carried out using lattice-Boltzmann method.
Shokouhmand et al. [26] numerically simulated the flow and heat transfer between two parallel plates of a conduit with porous core using lattice Boltzmann method. They investigated effects of various parameters such as Darcy number, porous medium thickness on the conduit thermal performance and showed that all these parameters have remarkable influence on thermal performance of the channel in certain conditions.
In previous studies [21,22,27] the lattice Boltzmann method was employed to investigate the effect of the heater location on flow pattern and heat transfer in a cavity numerically. Results showed that the location of heater and Rayleigh number have considerable effects on flow and temperature fields.
Heat generation in porous media takes place in some engineering applications such as electrically heat generating porous media or porous media as active layer in reacting chemical flows (catalyst layer in fuel cell). In this study the lattice Boltzmann method is used to simulate flow passing through a heat generating porous block located in a channel. The effects of flow Reynolds number, block porosity, porous block length over the fluid flow and heat transfer in the channel were investigated.
2. Materials and Methods
2.1. Lattice Boltzmann Method
In this simulation, a two dimensional model with nine velocities, D2Q9, has been used. The general form of Lattice Boltzmann equation with external force can be written as [15]:
![]() (1)
(1)
where Δt denotes lattice time step, ![]() is the discrete lattice velocity in direction k,
is the discrete lattice velocity in direction k, ![]() is the external force in direction k, τ denotes the lattice relaxation time, and
is the external force in direction k, τ denotes the lattice relaxation time, and![]() is the equilibrium distribution function which is calculated with:
is the equilibrium distribution function which is calculated with:
![]() (2)
(2)
where ωk is a weighting factor depending on the LB model used, ρis the lattice fluid density. The thermal LBM uses an extra distribution functions, g, for temperature field. The g distribution function would calculate as below [15]:
![]() (3)
(3)
The flow properties are defined as, ρ=∑kfk, ρui=∑kfkck and T=∑kgk , sub-index i denotes the component of the Cartesian coordinates.
The Brinkman-Forchheimer equation which has been used successfully in simulation of porous media [23,24,27,28] was used in this study. This equation after improving as below was used for both fluid and porous zones:
![]() (4)
(4)
where ε is the porosity of the medium, υeff is the effective viscosity, υ is the kinematic viscosity, and K is the permeability. For porous medium the equilibrium distribution functions are:
![]() (5)
(5)
In (1) the best choice for the forcing term, Fk is taking [23,24]:
![]() (6)
(6)
The matching conditions at the fluid-porous interface are satisfied automatically due to the unified governing equation (4). Therefore employing LBM significantly reduces the complexity of the traditional methods, which consider two regions separately. More information about porous media simulation with LBM is presented in [22,23,24].
To proper investigation of conjugate convection and conduction heat transfer in porous medium, the effective thermal conductivity of the porous medium (keff) should be identified, which was calculated by (Jiang et al. [30]):
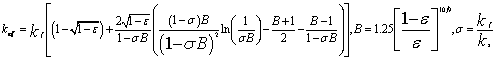 (7)
(7)
kf and ks are fluid and solid thermal conductivities, respectively.
2.2. Boundary Conditions
From the streaming process the distribution functions out of the domain are known. The unknown distribution functions are those toward the domain. Regarding the boundary conditions of the flow field, the solid walls are assumed to be no slip, and thus the bounce-back scheme is applied. This scheme specifies the outgoing directions of the distribution functions as the reverse of the incoming directions at the boundary sites.
For isothermal boundaries such as bottom wall the unknown distribution functions are evaluates as:
![]() (8)
(8)
2.3. Computational Domain
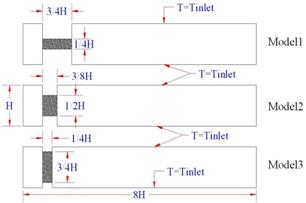
Figure 1. The computational domain.
Computational domain consists of a heat generating porous block which is located between two obstacles in a channel, Fig. 1. The effects of flow Reynolds number, porous block porosity and length over the fluid flow and heat transfer in the channel were investigated. The working fluid was air and porous matrix material was metal (Aluminum) and thermal conductivity ratio was set asσ=1.0×10-4. The flow was set fully developed at the inlet. The fluid at the inlet and all upper and bottom walls in clear channel as well as in contact with porous media are in same temperature, Tinlet. Other parameters of simulation are presented in Table 1.
Local and average Nusselt numbers are defined on isothermal walls in x and y directions as below:
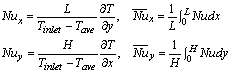 (9)
(9)
Table 1. Simulation parameters.
| Re | 20, 30, 40, 50 |
| Pr | 0.7 |
| Tinlet | 50°C |
|
| 0.3, 0.5, 0.7, 0.9 |
| Da | 0.001 |
| σ | 10-1-10-4 |
| S | 10W |
2.4. Validation and Grid Check
Table 2. Comparison of averaged Nusselt number between LBM and Kays and Crawford [31].
| Heat Flux Ratio | 0.5 | 1.0 | 1.5 | |
|
| Kays and Crawford [31] | 8.23 | 8.23 | 11.19 |
| Present Study (LBM) | 8.16 | 8.16 | 11.10 | |
|
| Kays and Crawford [31] | 8.23 | 8.23 | 7.00 |
| Present Study (LBM) | 8.16 | 8.16 | 6.91 |
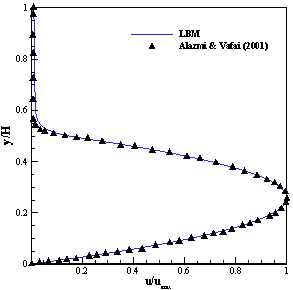
Figure 2. Comparison of velocity profile for partially filled channel with porous media between present model and Alazmi & Vafai [8] (Model 1).
In this study two dimensional thermal lattice Boltzmann method was employed to simulate flow and thermal fields in both clear and porous zones. Table 2, illustrates a good agreement between obtained Nusselt number by LBM and Kays and Crawford [31] for flow in clear channel. Another validation has been carried out for flow in the channel partially filled by porous medium, Figure 2. Regarding comparison between results of present simulation and Alazmi and Vafai study [8] it can be seen that present model indicates appropriate accuracy in predicting velocity profile in clear and porous zone and their interface.
For grid independency check, the averaged outlet and fluid temperature were calculated at different grid points. The grid point 40×320 was selected for simulations due to the results of the Table 3 and time saving.
Table 3. Comparison of outlet and fluid averaged temperatures at different grids.
| No. | Lattices | Tave-out(K) | Tave-fluid(K) |
| 1 | 35×280 | 340.11 | 344.31 |
| 2 | 40×320 | 340.26 | 344.39 |
| 3 | 45×360 | 340.87 | 344.88 |
| 4 | 50×400 | 341.2 | 345.38 |
3. Results and Discussion
Simulations of flow in three models which have identical surface were carried out with Lattice Boltzmann Method. The influence of different operating parameters on the fluid dynamics as well as on the heat transfer is discussed in following paragraphs.
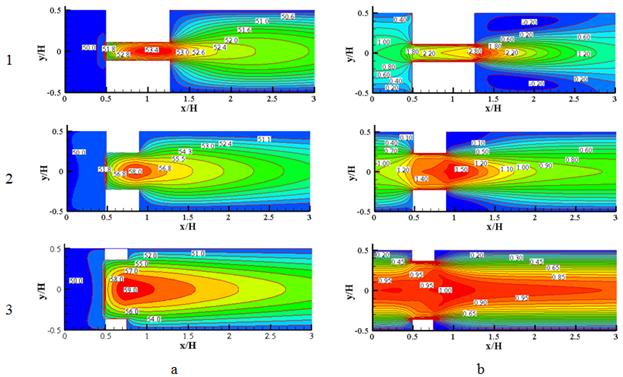
Figure 3. a) Temperature contours (°C), b) Contours of ![]() for different models (Re=40, ε=0.5, σ=10-3).
for different models (Re=40, ε=0.5, σ=10-3).

Figure 4. Effect of different values of porosity for the second model at Re=40, σ=10-3, a) Temperature contour (° C), b) velocity contours ![]() .
.

Figure 5. Effect of different Reynolds number for model 1, ε=0.5, σ=10-3, a) Temperature contours, b) velocity contours ![]() .
.
Temperature and velocity (![]() ) contours for different models are shown in Fig. 3. As can be viewed, once porous block's height rises in constant value of porosity and Reynolds number, maximum temperature of fluid increases.
) contours for different models are shown in Fig. 3. As can be viewed, once porous block's height rises in constant value of porosity and Reynolds number, maximum temperature of fluid increases.
Fig. 4 indicates the effect of porosity on heat transfer and fluid flow. Increasing porosity results an enhancement in fluid's temperature because of less heat transfer with adjacent cold walls. As porosity decreases, it would cause a growth in effective thermal conductivity due to development of solid's zone in porous block. So, there would be more heat transfer between fluid in porous block and cold isotherm walls and as a consequence fluid temperature declines. Furthermore, following of decreasing porosity, resistant force against fluid flow would be increased which causes an enhancement in boundary layer's thickness. With attention to constant profile of fluid's velocity at inlet, fluid's maximum velocity would increase. As can be seen in Fig. 4b, higher boundary layer's thickness and fluid's velocity at ɛ=0.3 has been caused a reverse flow region and vortex behind obstacles. Same behavior in Fig. 4 was observed for model 1 and model 3 like this model. Fig. 5a illustrates temperature contours of model 1 in constant value of porosity (ɛ=0.5) for different Reynolds numbers. Higher fluid's velocity reduces the time of heat transfer between fluid and heat source in porous block so fluid's temperature would diminish.
Temperature contours for different values of σ (=kf / ks) at three mentioned models while porosity and Reynolds are constant (ɛ=0.5, Re=40) have been plotted, Figs. 6-8. Increase in thermal conductivity coefficient of solid zone (ks) causes a growth in effective thermal conductivity coefficient (keff) of porous block. So there would be more heat transfer with adjacent isotherm cold walls. As a consequence, fluid's temperature would be declined.
Fig. 9a shows temperature contours in different values of Reynolds numbers for model 3. Fluid's temperature would stay constant from inlet to porous zone which is equal to inlet temperature.
By entering fluid to porous block, an abrupt surge would occur in fluid's temperature due to heat generating source in porous block. After porous region, heat transfer with upper and bottom walls would reduce fluid's temperature slightly. As it is shown in Fig. 9a, since advection occurs in porous zone, maximum temperature occurs near the end part of porous block not at the center.
Additionally, for fixed heat generating fluid temperature increases in lower velocities due to the heat transfer equation (![]() , which Q is fixed in all velocities, u).
, which Q is fixed in all velocities, u).
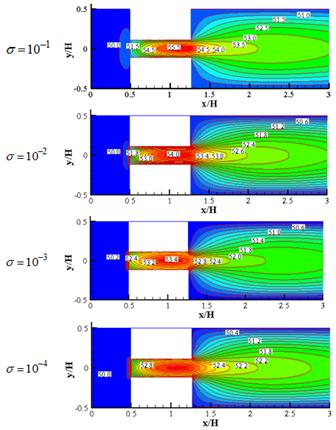
Figure 6. Temperature contours for model 1 at ![]() ,
, ![]() and different values of
and different values of![]() .
.
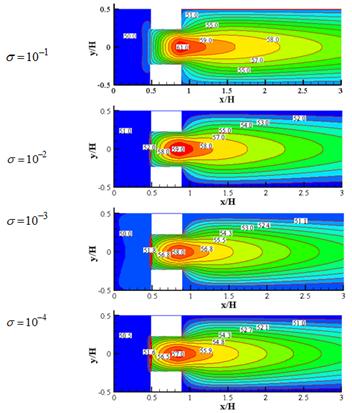
Figure 7. Temperature contours for model 2 at![]() , Re=4 and different values of σ.
, Re=4 and different values of σ.
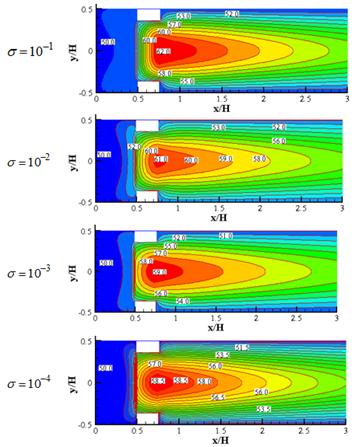
Figure 8. Temperature contours for model 3 at![]() , Re=40 and different values of
, Re=40 and different values of![]() .
.
Therefore maximum temperature in porous block was seen at Re=20.Furthermore, after porous block this lower velocity causes more heat transfer time with isotherm cold walls and consequently minimum temperature at outlet belongs toRe=20.
Fig. 9b shows averaged Nusselt number variation with Reynolds number. Increase in Reynolds number would change the prevailing heat transfer mechanism from diffusion to advection, so Nusselt number would develop. This change in heat transfer mechanism leads that fluid get less heat from porous heat source. So with rise in Reynolds number, maximum temperature would decrease.
According to the above evaluations about different effects of fluid's velocity inside and after porous block, although with rise in Reynolds number maximum temperature decreases, averaged fluid temperature would be enhanced, Fig. 9c. By increase in Reynolds number there would be less heat transfer between fluid and heat source in porous block. Moreover, heat transfer with cold adjacent walls would enhance because of increase in Nusselt number. But as can be viewed from velocity contours in Fig. 5, by increase in Reynolds number, fluid flow state after porous block would become near to jet flow. This factor has more influence on averaged fluid temperature than two previous ones. In porous block according to (7) effective thermal conductivity coefficient develops in comparison with clear zone. So more heat transfer with cold walls occurs in this part and consequently the model which has the most contact length between porous block and cold walls (model 1) would have the lowest average temperature in contrast with other models (Figs. 3 and 9c).

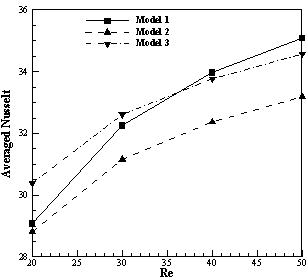
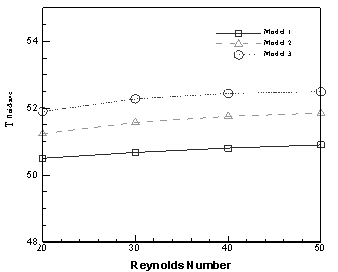
Figure 9. a) Mid-height temperature at different Reynolds number for model 3; b) Averaged Nusselt number at different Reynolds number,![]() ; c) Averaged fluid temperature at different Reynolds number.
; c) Averaged fluid temperature at different Reynolds number.
4. Conclusion
In this paper a simulation of heat transfer and fluid flow in a channel with a heat generating porous block has been carried out by the use of Lattice Boltzmann method. The influences of various parameters have been evaluated. Results show that with rise in block's height (in constant value of block's surface), maximum velocity decreases in block. Furthermore, Fluid's temperature would enhance because of lower heat transfer with adjacent cold walls. Higher values of porosity lead to lower heat transfer with cold isotherm walls. So fluid's temperature would increase. As Reynolds number increases, maximum temperature in block would decrease. It's due to reduce in heat transfer between heat source and fluid. On the other hand, it was observed that averaged temperature has been developed. Actually it would develop with rise in block's height too. It is notable that porosity and block's height have more effect than concerned Reynolds numbers on fluid's temperature in block. Maximum temperature of fluid declines with rise in thermal conductivity of solid zone. It leads to growth in effective thermal conductivity and consequently more heat transfer with cold walls.
Nomenclature
BH: Block height (m)
BL: Block length (m)
c: Discrete lattice velocity
Da: Darcy Number [=K.H-2]
f: Distribution function for flow
F: Acceleration due to external force (m.sec-2)
G: Acceleration due to gravity (m.sec-2)
H: Characteristic height (m)
K: Permeability (m2)
L: Characteristic length (m)
Q: Heat source (W)
Re: Reynolds number [=uH.ʋ-1]
Nu: Nusselt number [=hL.k-1]
S: Source term (kg.m-3.s-1)
t: Time (sec)
T: Temperature (K)
u:Velocity component (m.sec-1)
x: Dimension (m)
q'': heat flux (W/m2)
k: Thermal conductivity coefficient (W/mK)
Greek symbols:
ε: is the porosity of porous media
μ: Dynamic viscosity (kg.m-1.s-1)
ρ: Density(kg.m-3)
υ: Kinematic viscosity(m2.s-1)
τ: Relaxation time
ω: Weighting factor
σ: kf / ks
Subscripts and superscripts:
*: Non-dimensional
b_w: from block to adjacent walls
i: Dimension direction
k: Lattice model Direction
s: Sound
wall: Horizontal walls of channel after block
References
- Kaviany, M., 1985. Laminar flow through a porous channel bounded by isothermal parallel plates. Int. J. Heat Mass Transfer. 28, 851–858.
- Hunt, M.L., Tien, C.L., 1988. Effects of thermal dispersion on forced convection in fibrous media. Int. J. Heat Mass Transfer. 31, 301–309.
- Vafai, K., Kim, S.J., 1989. Forced convection in a channel filled with a porous medium: an exact solution. ASME J. Heat Transfer. 111, 1103–1106.
- Hossain, M.A., Vafai, K., Khanafer, M.N., 1999. Non-Darcy natural convection heat and mass transfer along a vertical permeable cylinder embedded in a porous medium. Int. J. Therm. Sci. 38, 854–862.
- Zhang, B., Zhao, Y., 2000. A numerical method for simulation of forced convection in a composite porous/fluid system. Int. J. Heat and Fluid Flow. 21, 432–441.
- Jeng, T.M., 2008. A porous model for the square pin-fin heat sink situated in a rectangular channel with laminar side-bypass flow. Int. J. Heat and Mass Transfer. 51, 2214–2226.
- Li, H.Y., Leong, K.C., Jin, L.W., Chai, J.C., 2010. Analysis of fluid flow and heat transfer in a channel with staggered porous blocks. Int. J. Thermal Sciences. 49, 950–962
- Alazmi, B., Vafai, K., 2001. Analysis of fluid flow and heat transfer interfacial conditions between a porous medium and a fluid layer. Int. J. of Heat and Mass Transfer. 44, 1735–1749.
- Khanafer, Kh., Chamkha, A.J., 2003. Mixed convection within a porous heat generating horizontal annulus. Int. J. of Heat and Mass Transfer. 46, 1725–1735.
- Narasimhan, A., Reddy, B.V.K., 2011. Laminar forced convection in a heat generating bi-disperse porous medium channel. Int. J. of Heat and Mass Transfer. 54, 636–644.
- Jeng, T.M., Wang, M.P., Hwang, G.J., Hung, Y.H., 2004. A new semi-empirical model for predicting heat transfer characteristics in porous channels. Exp. Thermal and Fluid Science. 29, 9–21.
- Chen, S., Doolen, G.D., 1998. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 30, 329–364.
- Succi, S., 2001. The Lattice Boltzmann Equation for Fluid Dynamics and Beyond. Clarendon Press, Oxford.
- Yu, D., Mei, R., Luo, L.S., Shyy, W., 2003. Viscous flow computations with the method of lattice Boltzmann equation. Progr. Aerospace Sci. 39, 329–367.
- Mohamad A A (2011) Lattice Boltzmann Method, Fundamentals and Engineering Applications with Computer Codes, Springer, London, England
- Kao, P.H., Chen, Y.H., Yang, R.J., 2008. Simulations of the macroscopic and mesoscopic natural convection flows within rectangular cavities. Int. J. Heat and Mass Transfer. 51, 3776–3793.
- Chopard, B., Luthi, P.O., 1999. Lattice Boltzmann computations and applications to physics. Theor. Comput. Phys. 217, 115–130.
- Von der Sman, R.G.M., Ernst, M.H., Berkerbosch, A.C., 2000. Lattice Boltzmann scheme for cooling of packed cut flowers. Int. J. Heat Mass Transfer. 43, 577–587.
- Ho, J.R., Kuo, C.P., Jiaung, W.S., 2003. Study of heat transfer in multilayered structure within the framework of dualphase-lag heat conduction model using lattice Boltzmann method. Int. J. Heat Mass Transfer. 46, 55–69.
- Nourgaliev, R.R., Dinh, T.N., Theofanous, T.G., Joseph, D., 2003. The lattice Boltzmann equation method: theoretical interpretation, numerics and implications. Int. J. Multiphase Flow. 29, 117–169.
- Delavar, M.A., Farhadi, M., Sedighi, K., 2009. Effect of the heater location on heat transfer and entropy generation in the cavity using the lattice Boltzmann Method. Heat Transfer Research. 40 (6), 521–536.
- Delavar, M.A., Farhadi, M., Sedighi, K., 2010. Numerical simulation of direct methanol fuel cells using lattice Boltzmann method. Int. Hydrogen Energy. 35, 9306–9317.
- Seta, T., Takegushi, E., Kitano, K., Okui, K., 2006. Thermal Lattice Boltzmann Model for Incompressible Flows through Porous Media. J. of Thermal Science and Technology, 1, 90–100.
- Seta, T., Takegoshi, E., Okui, K., 2006 Lattice Boltzmann simulation of natural convection in porous media, Mathematics and Computers in Simulation. 72, 195–200.
- Mantle, M.D., Bijeljic, B. Sedermana, A.J., Gladdena, L.F., 2001. MRI velocimetry and lattice-Boltzmann simulations of viscous flow of a Newtonian liquid through a dual porosity fibre array. Magn. Reson. Imaging 19, 527–529.
- Shokouhmand, H., Jam, F., Salimpour, M.R., 2009. Simulation of laminar flow and convective heat transfer in conduits filled with porous media using Lattice Boltzmann Method. International Communications in Heat and Mass Transfer. 36, 378–384.
- Delavar, M. A., Heat Transfer Asian research, 2012
- Kiwan, S., Khodier, M., 2008. Natural Convection Heat Transfer in an Open-Ended Inclined Channel-Partially Filled with Porous Media. Heat Transfer Engineering, 29(1), 67-75.
- Delavar, M.A., Farhadi, M., Sedighi, K., 2011. Effect of discrete heater at the vertical wall of the cavity over the heat transfer and entropy generation using LBM. Thermal Science. Vol. 15, No. 2, 423–435.
- Jiang, P.-X., Lu, X.-C., 2006. Numerical simulation of fluid flow and convection heat transfer in sintered porous plate channels. Int. J. of Heat and Mass Transfer. 49, 1685–1695.
- Kays, W.M., Crawford, M.E., 1993. Solutions Manual, Convective Heat and Mass Transfer, third ed. McGraw-Hill, New York, Problem 9-1.



