Numerical Simulation of Turbulent Thermo-Fluid Dynamics in Wavy Microchannel
CFD-Lab, Mechanical Engineering Dept., Faculty of Engineering, Taif University, Al-Haweiah, Taif, Saudi Arabia
Abstract
The hydrodynamic and thermal behaviors of fluid flow in turbulent wavy microchannel are investigated numerically. Effects of Reynolds number on the hydrodynamics and thermal behaviours are investigated. Three different values of Reynolds number (28.7, 38, and 48.7) are adopted in this study. A new numerical method based on the so-called fraction-step method is developed. The control volume approach is applied for solving the Reynolds-Averaged Navier-Stokes (RANS) Equations. The standard k-epsilon turbulence model is used to predict the turbulence characteristics inside the wavy microchannel. It is found that, the maximum temperature and velocity at the center line at the mid-section of the wave increases as Reynolds number increases. Also, it is found the maximum temperature at the end section of the wave vanishes for small values of Reynolds number (Re < 28.7) for turbulent flow, while there is a contradiction at the mid-section of the wave.
Keywords
Thermo-Fluid Behavior, Turbulent Flow, Microelectronic Devices, Numerical Simulation, Wavy Microchannel
Received:May 7, 2015
Accepted: May 14, 2015
Published online: June 12, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
Due to ever increase in miniaturization of electronic packages and rapid boost in power density, the conventional cooling solutions based on fans and/or metal fins are becoming unrealistic and unable to meet the increasing demand of the cooling of emerging electronic devices. The thermal issues of the electronic devices are now such a critical concern that they have become the bottleneck for further development of advanced electronic products. Due to lack of advanced, more effective and innovative cooling methods, the die temperatures might inevitably escalate, ultimately resulting in reduced mean-time-to-failure and associated performance degradation.
The innovative technique of direct liquid cooling which essentially employs micro-channels is a promising solution to the problem [1–7]. The technique might involve single- phase cooling or two-phase (boiling) cooling. Although the latter has potentially higher heat removal capacity, it involves complex issues such as saturation temperature, condensation, nucleation site activation and critical heat flux etc. For problems involving an intermediate level of heat flux removal, the single-phase cooling offers an alternative solution that is simpler to implement yet gives the desired results [4]. In case of single-phase cooling, due to the compact feature size of micro-channels and the related higher influence of surface tension, higher flow rates (high Reynolds numbers) cause a sharp increase in pressure loss and hence increased demand of pumping power.
In a recent numerical study involving fully developed laminar flow and heat transfer in periodic serpentine channels with various cross-section shapes, Fletcher et. al. [8–12] reported that Dean Vortices and more complex vertical flow patterns emerged when the liquid coolant flowed through the bends. It was found that the heat transfer performance was remarkably enhanced over straight channels involving the same cross section. Also, the pressure drop penalty was much smaller compared to the gain of heat transfer enhancement.
The laminar force convection in wavy-plate-fin channels under periodically developed air flow condition was investigated numerically by Manglik et. al [13,14]. In the two-dimensional simulation it was showed that the flow was characterized by lateral swirl or fluid recirculation in the trough regions of the wavy channel. However, the three-dimensional simulation of the same problem revealed symmetric Dean Vortex pairs in the cross sections of the sinusoidal channels. All these researches involved the conventional straight micro-channels. There is and increased interests in research of micro sized cooling devices over the last several years [15-20].
In the present work thermal and hydrodynamic behaviors of fluid flow in wavy microchannel are investigated numerically. Effect of different cases of Reynolds number is investigated in this study. The thermal and hydrodynamics behaviors are investigated under these cases. The numerical procedure developed in this work is based on the control volume approach proposed by Patankar [21].
2. Material and Methods
In wavy microchannel environment, shown in Fig.1, the thermally turbulent flow is governed by the continuity, momentum and energy equations for unsteady, incompressible and Newtonian flow.
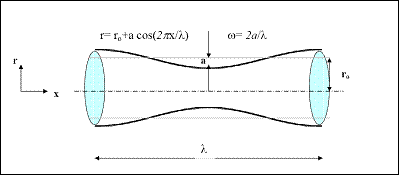
Figure 1. Configuration of wavy microchannel.
Regarding above assumptions, the governing equations are written in the form of the unsteady Reynolds-averaged Navier-Stokes (RANS) equations coupled with the standard k-e model can be written as follows:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
In the above system of equations, r is the density, ![]() is the velocity vector, p is the static pressure, T is the temperature,
is the velocity vector, p is the static pressure, T is the temperature, ![]() is the heat flux vector, Cp is the specific heat capacity at constant pressure, m is the molecular viscosity, mt is the turbulent viscosity, k is the turbulent kinetic energy, e is the turbulent dissipation,
is the heat flux vector, Cp is the specific heat capacity at constant pressure, m is the molecular viscosity, mt is the turbulent viscosity, k is the turbulent kinetic energy, e is the turbulent dissipation, ![]() and
and ![]() are the strain rate tensor and turbulent stress tensor respectively. The components of the strain rate tensor can be described as:
are the strain rate tensor and turbulent stress tensor respectively. The components of the strain rate tensor can be described as:
![]() (6)
(6)
and the turbulent stress tensor is given by:
![]() (7)
(7)
where ![]() is the kronecker delta and
is the kronecker delta and ![]() is the average of the velocity fluctuations. The turbulent viscosity is defined as:
is the average of the velocity fluctuations. The turbulent viscosity is defined as:
![]() (8)
(8)
The coefficients for the modified turbulence model adopted in the present work are given as follows
![]()
The heat flux vector consists of a molecular and turbulent part:
![]() (9)
(9)
The turbulent Prandtl number is Prt = 0.9, while the molecular Prandtl number Pr and the specific heat capacity at constant pressure are defined according to the fluid considered.
The numerical procedure developed in the present work is based on the control volume approach proposed by [21]. In such approach, a general differential equation for the dependent variables (u, v, T, k, e) is written for unsteady, Newtonian, two-dimensional (![]() )/axisymmetric (
)/axisymmetric (![]() ) and incompressible flow as follows:
) and incompressible flow as follows:
![]() (10)
(10)
where ![]() is the dependent variable,
is the dependent variable, ![]() is the diffusion coefficient for
is the diffusion coefficient for ![]() , and
, and ![]() is the source term. The quantities
is the source term. The quantities ![]() and
and ![]() are specific to a particular meaning of
are specific to a particular meaning of![]() . Using the control volume arrangement proposed by [21], the above general differential equation can be written in terms of the total fluxes over the control volume faces and the resulting equation is integrated over each control volume. In similar manner, the continuity equation is integrated over the control volume.
. Using the control volume arrangement proposed by [21], the above general differential equation can be written in terms of the total fluxes over the control volume faces and the resulting equation is integrated over each control volume. In similar manner, the continuity equation is integrated over the control volume.
In our algorithm, one can assume that the velocity field reaches its final value in two stages; that means
![]() (11)
(11)
whereby, ![]() is an imperfect velocity field based on a guessed pressure field, and
is an imperfect velocity field based on a guessed pressure field, and ![]() is the corresponding velocity correction. Firstly, the 'starred' velocity will result from the solution of the momentum equations. The second stage is the solution of Poisson equation for the pressure
is the corresponding velocity correction. Firstly, the 'starred' velocity will result from the solution of the momentum equations. The second stage is the solution of Poisson equation for the pressure
![]() (12)
(12)
where ![]() will be called the pressure correction and
will be called the pressure correction and ![]() is the chosen time step. Once this equation is solved, one gets the appropriate pressure correction, and consequently, the velocity correction is obtained according to:
is the chosen time step. Once this equation is solved, one gets the appropriate pressure correction, and consequently, the velocity correction is obtained according to:
![]() (13)
(13)
The fractional step non-iterative method described above ensures the proper velocity-pressure coupling for incompressible flow field. It should be pointed out that the above numerical method has been developed and successfully applied for simulating a variety of engineering applications [22-25].
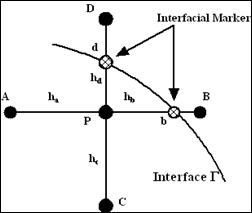
Figure 2. Calculation of the interphase boundary values.
In order to accurately calculate the surface force that included in the momentum equations a simple linear interpolation is used firstly to calculate any property of the interface from the known internal grid point’s values. According to Fig. 2, the Poisson equation for pressure is approximated at point p as follows:
![]() (14)
(14)
where Sp is the source term described in Eq. (12).
3. Result and Discussions
Numerical simulation of fluid behavior in turbulent wavy microchannel used in microelectronic devices is investigated in this study. Axial velocity distribution and the velocity vector plot for different cases listed in Table 1, where case I (Re=28.7), case II (Re=38), and case III (Re=48.7) respectively.
Table I. Numerical parameters of micro wave.
| Case | |||
| Case I | 28.7 | 0.002 | 251.3 |
| Case II | 38 | 0.002 | 251.3 |
| Case III | 48.7 | 0.002 | 251.3 |
Figure 3 shows that the centerline velocity increases as the Reynolds number increases for the same wave ratio. This increase is due to the satisfying of the continuity equation; especially at the midsection of the wave.
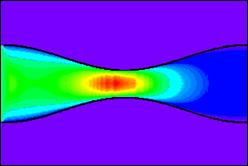
(a)
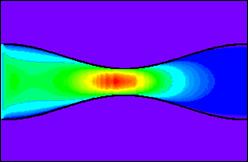
(b)

(c)
Figure 3. Axial velocity distribution for (a) case I, (b) case II, and (c) case III.
Figure 4 indicates that the same behavior for the axial velocity distribution in form of vector plots.
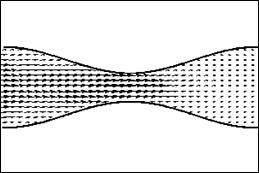
(a)
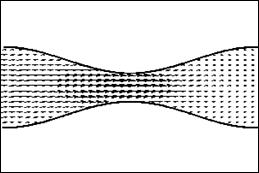
(b)
Figure 4. Velocity vector plot for (a) case I and (b) case III.
Figures (5&6) show the dimensionless velocity distribution at the mid and end-sections of the wave for the different cases considered. It is clear that the dimensionless maximum velocity at the center line at the mid and end-sections of the wave increases as Reynolds number increases.
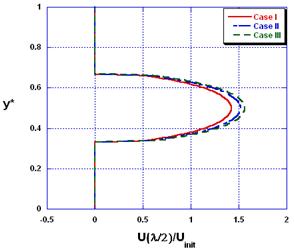
Figure 5. Velocity profiles at the mid-section of the wave for the different cases considered.
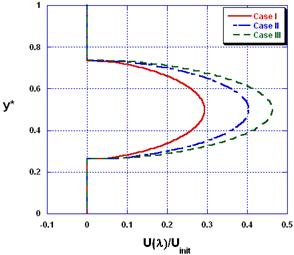
Figure 6. Velocity profiles at the end-section of the wave for the different cases considered.
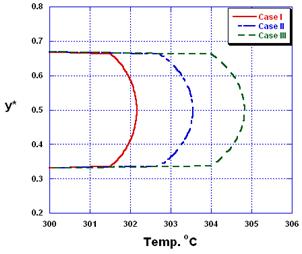
Figure 7. Temperature profiles at the mid-section of the wave for the different cases considered.
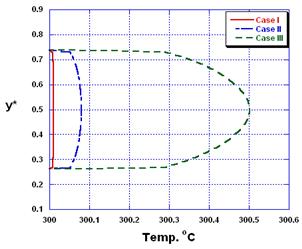
Figure 8. Temperature profiles at the end-section of the wave for the different cases considered.
Figures (7&8) show the temperature profiles at the mid and end sections of the wave for the different cases considered in this study. It can be seen that, by increasing the Reynolds number, the maximum temperature increases at both the midsection and the end-section as well. However, the increase of the maximum centerline temperature at the end-section is much visible.
Figure 9 shows the distribution of the turbulent kinetic energy predicted by the standard k-epsilon model inside the wavy microchannel. In all three cases, the turbulent kinetic energy increases in the midsection of the wavy microchannel. However, the effect of Reynolds number on the turbulent kinetic energy distribution could not be evaluated due to the small range of the Reynolds number considered in the present study.
(a)

(b)

(c)
Figure 9. Turbulent kinetic energy distribution for (a) case I, (b) case II, and (c) case III.
4. Conclusions
Numerical simulation of fluid behavior in wavy microchannel used in microelectronic devices is investigated in this study. Effects of Reynolds number on the velocity and temperature behaviors are investigated. Three cases of Reynolds number (28.7, 38, and 48.7) are applied in this study. The obtained results showed that the numerical method adopted is capable of predicting such dynamics in such complex geometry.
References
- I. Hassan, P. Phutthavong, M. Abdelgawad, Microchannel heat sinks: an over view of the state-of-the-art, Microscale Therm. Eng. 8 (2004) 183–205.
- D.B. Tuckerman, R.F.W. Pease, High-performance heat-sinking for VLSI, IEEE Electr. Dev. L. 2 (5) (1981) 126–129.
- M.K. Kang, J.H. Shin, H.H. Lee, K. Chun, Analysis of laminar convective heat transfer in micro heat exchanger for stacked multi-chip module, Microsyst. Technol. 11 (2005) 1176–1186.
- S.G. Kandlikar, W.J. Grande, Evaluation of single phase flow in microchannels for high heat flux chip cooling – thermohydraulic performance enhancement and fabrication technology, Heat Transfer Eng. 25 (8) (2004) 5–16.
- P.S. Lee, S.V. Garimella, D. Liu, Experimental investigation of heat transfer in microchannels, Int. J. Heat Mass Transfer 48 (2005) 1688–1704.
- S.V. Garimella, C.B. Sobhan, Transport in microchannels – a critical review, Annu. Rev. Heat Transfer 13 (2003) 1–50.
- P.S. Lee, S.V. Garimella, Thermally developing flow and heat transfer in rectangular microchannels of different aspect ratios, Int. J. Heat Mass Transfer 49 (2006) 3060–3067.
- N.R. Rosaguti, D.F. Fletcher, B.S. Haynes, Laminar flow and heat transfer in a periodic serpentine channel with semi-circular crosssection, Int. J. Heat Mass Transfer 49 (17-18) (2006) 2912–2923.
- N.R. Rosaguti, D.F. Fletcher, B.S. Haynes, Laminar flow and heat transfer in a periodic serpentine channel, Chem. Eng. Technol. 28 (3) (2005) 353–361.
- P.E. Geyer, N.R. Rosaguti, D.F. Fletcher, B.S. Haynes, Laminar flow and heat transfer in periodic serpentine mini-channels, J. Enhanced Heat Transfer 13 (4) (2006) 309–320.
- P.E. Geyer, N.R. Rosaguti, D.F. Fletcher, B.S. Haynes, Laminar thermohydraulics of square ducts following a serpentine channel path, Microfluid. Nanofluid. 2 (3) (2006) 195–204.
- P.E. Geyer, D.F. Fletcher, B.S. Haynes, Laminar flow and heat transfer in a periodic trapezoidal channel with semi-circular crosssection, Int. J. Heat Mass Transfer 50 (17–18) (2006), 3471–3480.
- R.M. Manglik, J. Zhang, A. Muley, Low Reynolds number forced convection in three-dimensional wavy-plate-fin compact channels: fin density effects, Int. J. Heat Mass Transfer 48 (8) (2005) 1439–1449.
- H.M. Metwally, R.M. Manglik, Enhanced heat transfer due to curvatureinduced lateral vortices in laminar flows in sinusoidal corrugated-plate channels, Int. J. Heat Mass Transfer 47 (10–11) (2004) 2282–2292.
- A. F. Khadrawi, A. Othman and M. A. Al-Nimr, Transient free convection fluid flow in a vertical microchannel as described by the hyperbolic heat conduction model, Int. J. Thermophysics, Vol. 26, pp.905, 2005.
- M. A. Al-Nimr, and A. F. Khadrawi, Thermal behavior of a stagnant gas convicted in a horizontal microchannel as described by the dual-phase-lag heat conduction model, Int. J. Thermophysics, Vol. 25, pp. 1953, 2004.
- J. Al-Jarrah, A. F. Khadrawi, and M. A. Al-Nimr, Film condensation on a vertical micro-channel, Int. Communication in Heat and Mass Transfer, Vol. 35(9), pp. 1172-1176, 2008.
- A. F. Khadrawi and Ahmad Al-Shyyab, Slip Flow and Heat Transfer in Axially Moving Micro-Concentric cylinders,International Communications in Heat and Mass Transfer, 37, 8, pp.1149–1152, 2010.
- M. A., Al-Nimr, A. M., Maqapleh, A. F. Khadrawi, and Ammourah S. A.: "Fully developed thermal behaviors for parallel flow microchannel heat exchanger", International Communications in Heat and Mass Transfer Vol. 36, pp 385–390, 2009.
- M. Maqableh, A. F. Khadrawi, M. A. Al-Nimr, S. A. Ammourah and A. C. Benim, "Heat Transfer Characteristics of Parallel and Counter Flow Microchannel Heat Exchangers with Varying Wall Resistance" Progress in Computational Fluid Dynamics, 11(5), pp. 318-328, 2013.
- Patankar, SV. Numerical Heat Transfer and Fluid Flow. Hemisphere Publishing Corporation 1980.
- Balabel A. Numerical simulation of two-dimensional binary droplets collision outcomes using the level set method, International Journal of Computational Fluid Dynamics 2012;26(1): 1-21.
- Balabel A. Numerical Prediction of Turbulent Thermocapillary Convection in superposed Fluid Layers with a free Interface, International Journal of Heat and Fluid Flow 2011;32(6): 1226-1239.
- Balabel A. A New Numerical Method for Simulating Two-Fluid Interfacial Flow using Level Set Method, International Journal of Control, Automation and Systems 2013;.2(3): 31-40.
- Balabel A Numerical Modelling of Turbulence Effects on Droplet Collision Dynamics using the Level Set Method. Computer Modeling in Engineering and Sciences (CMES) 2012; 89(4):283-301.



