The Sea Level Rate of Rise and the Subsidence Rate Are Constant in Fremantle
A. Parker*
School of Engineering and Physical Science, James Cook University, Townsville, Australia
Abstract
The paper discusses a claim of variable subsidence rate of -2 to -4 mm per year for the Fremantle tide gauge (TG). It is shown as the GPS monitoring is still progressing, and far from delivering accurate subsidence rates of inland domes far from the TG location with relative motion unassessed. It is also shown as the TG signal of Fremantle shows natural oscillations of the relative sea levels up to a quasi-60 years’ multi-decadal periodicity about a constant trend SLR,R of about +1.7 mm/year over more than one century. It is concluded that the most likely subsidence rate of the TG instrument VLM is -1.7 mm/year and constant.
Keywords
GPS, Time Series, Fremantle
Received:May 30, 2016
Accepted: August 10, 2016
Published online: August 19, 2016
@ 2016 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY license. http://creativecommons.org/licenses/by/4.0/
1. Introduction
In the past, it was customary to refer vertical positions on Earth to the mean sea level (MSL) taken as zero. This is certainly not a precise, modern, assumption, as the MSL may change, for example by mass addition from melting of ice on land or by thermal expansion for warming of oceans, but also because of the natural fluctuations of well-known periodicities up to multi-decadal.
The tide gauges (TG) are providing relative MSL measurements. In the best cases, the length of the tide gauges’ time series exceeds one century. Fremantle and Sydney, Fort Denison are the only two tide gauge of the Southern Hemisphere with record start prior of the year 1900 and presently operational [1].
The TG MSL time series permit to infer, if they are long enough and the data have no quality issues, the relative rate of rise of sea levels SLR,R and eventually the relative sea level acceleration SLA,R. If the subsidence of the TG instrument does not change, this relative acceleration is equal to the absolute sea level acceleration SLA,A [2-6].
The SLR,R results usually suggest slow rising not accelerating relative patterns, i.e. usually small positive or negative SLR,R and negligibly small positive or negative SLA,R [2-6].
The TG MSL result alone does not permit any direct estimation of mass addition from melting of ice on land, or thermal expansion for warming of oceans, or computation of absolute sea level velocities SLR,A, that differ from the relative for the absolute tide gauge instrument velocity VLM, as SLR,A=SLR,R-VLM.
Different products are being developed to measure the vertical velocity of the tide gauge VLM. The most promising are the Global Positioning System (GPS) time series of nearby GPS domes [7,8] and the precise levelling of the TG vs. the GPS dome that unfortunately is usually omitted.
Alternatively, the satellite altimetry corrected for a modelled Glacial Isostatic Adjustment (GIA) may be used to compute the global mean sea level (GMSL) [6,9]. The GMSL time series may then be used to infer absolute sea level velocities SLR,A.
If in principle the SLR,A from the satellite altimeter signal corrected for the GIA should be equal the TG SLR,R corrected for the TG VLM from the GPS time series of a nearby GPS dome and the relative levelling, in practice this is not the case.
The GPS positioning and the satellite altimetry all suffer of inaccuracy usually larger than the relative sea level trend [6]. Additionally, the satellite GMSL is more a sort of non-validated computational product than a measurement. The absolute GMSL estimation is indeed an almost un-trended and inaccurate signal tilted by arbitrary computational GIA to about +3 mm/year everywhere [6].
2. GPS Tracking of the Perth Dome by SONEL and JPL
Ref. [10] claims that the GPS derived vertical land motion (VLM) must be geodetically connected to the TG to eliminate the commonly used assumption that there is no differential VLM when the GPS is not co-located with the TG. This is certainly correct. But this is not the only problem, as the GPS monitoring is inaccurate, and the satellite altimetry unreliable.
The GPS of Perth is an inland dome located at Longitude 115.88525002, Latitude -31.80196686 and Height 12.7106 m. It is many kilometers far from the coastal tide gauge of Fremantle having Latitude -32.065556 and Longitude 115.748139.
The GPS tracking of the Perth dome is certainly not an accurate representation of the vertical velocity of the tide gauge of Fremantle for two reason, because the relative motion tide gauge vs. GPS dome is unassessed, and because the GPS signal for a dome suffers of many biases and needs many corrections resulting in inaccurate velocity results.
The present estimations of the VLM based on the GPS monitoring are everything but very accurate, as the satellite periodic drift and other perturbing factors return time series quite difficult to analyze. So, even if the GPS dome would be co-located with the TG, the accuracy of the computation of the TG VLM would not be perfect.
The SONEL analysis of the Perth (PERT) GPS dome time series, see figure 1 (from [7]), has 6 offsets over 6 years of recording, suggesting a subsidence of -2.99 mm/year not certainly subject to an error of ±0.34 mm/year that is only the fitting error by assuming every point is a perfect measurement.
Based on pretty much the same data and the same computational framework, the not independent JPL analysis, see figure 2 (from [8]) returns indeed a different subsidence velocity of -2.201 mm/year, with again an error of ±0.543 mm/year that is only the fitting error by assuming every point is a perfect measurement.
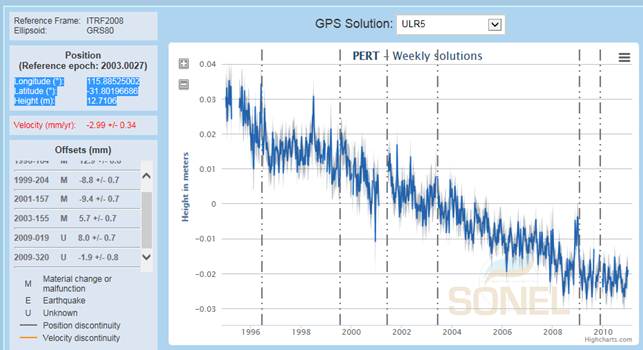
Figure 1. PERT (PERTH) GPS dome analysis by SONEL (from [7]).
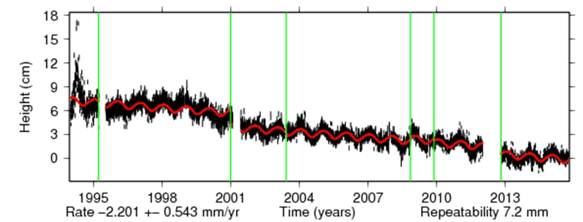
Figure 2. PERT (PERTH) GPS dome analysis by JPL (from [8]).
Another GPS dome nearby the Fremantle tide gauge is considered by SONEL. It is HIL1 (HILLARYS), Figure 3, of Longitude 115.73858129, Latitude -31.82552451 and Height -27.2276 m (minus 27.2276 m) according to SONEL. The signal is considered not robust by SONEL. The likely subsidence of the proposed signal having only 1 offset is about 16 mm over 4 years, or -4 mm/year.

Figure 3. HIL1 (HILLARYS) GPS dome analysis by SONEL (from [11]).
3. Reliability and Accuracy of the GPS Estimations by SONEL and JPL
How reliable and accurate are the GPS estimations by SONEL and JPL of the Fremantle TG VLV it is difficult to say. As shown in Figures 1 and 2, two collaborating institutions suggest on the basis of pretty much same data results quite different. For PERT, the differences in between the SONEL and the JPL analyses developed from about same data with about same constraints are not dramatic, but still a remarkable 0.69 mm/year. There are many other cases where differences are larger. For example, the UCLU GPS dome nearby the tide gauge of Tofino, BC, Canada or the PLO3 GPS dome nearby the San Diego, CA, USA tide gauge have vertical velocities of +4.10 and -1.65 mm/year according to SONEL but vertical velocities of +2.54 and -2.39 mm/year according to JPL.
Regarding the reliability, as the relative sea level velocity in Fremantle as discussed in the next section is +1.7 mm/year, the subsidence rate exceeds in this case the relative sea level velocity, i.e. the effect of mass addition because of melting of ices on land and thermal expansion because of the warming of the oceans is apparently negative in Fremantle. This is however not the case. The computations by SONEL and JPL are constrained, so basically if the subsidence is underrated in some areas (for example Europe or the United States where the most part of the tide gauges are concentrated), then the subsidence is overrated in others (for example Australia).
Figure 4 presents the absolute and relative sea level velocities from the GPS monitoring of SONEL and the tide gauges of PSMSL. In these images, only the tide gauges with a nearby robust GPS velocity by SONEL are displayed even for relative trends. The trends are computed for the time window 1900 to 2013 where there are at least 70% of valid data. The tide gauge sea level trends are retrieved and processed in real-time from the PSMSL. The images are from [12]. Clearly, the absolute sea level velocities in North Europe and North America much larger than the relative are obtained at the expenses of smaller then relative absolute sea level velocities in Australia, strongly negative in case of Fremantle.
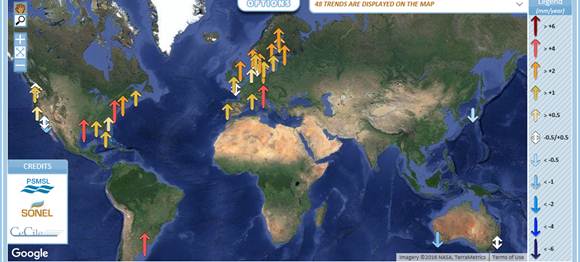
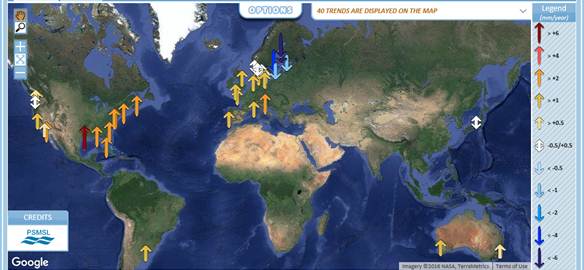
Figure 4. Absolute (top) and relative (bottom) sea level velocities from the GPS monitoring of SONEL and the tide gauges of PSMSL with time window 1900 to 2013. The images are from [12].
4. Relative Sea Level Velocities of Tide Gauges
The naïve average of the relative rate of rise SLR,R at the worldwide tide gauges of enough length and quality is a mere +0.19 mm/year, see Table 1 in the Appendix derived from [1]. This table is the summary of the relative rates of rise of the 108 worldwide tide gauges with more than 80 years of recording in the latest survey (2015) of the PSMSL data base [1]. Most of them have a positive trend, but many others have a negative trend, and the naïve average is only +0.19 mm/year. The largest relative sea level rise is +6.75 mm/year, the smallest -8.06 mm/year. As the multi-decadal oscillations that are suggesting much larger or much smaller than the true relative sea level rises are mostly cleared out after 80 years, this is an indication of the strongly differential subsidence worldwide that makes a non-sense to talk about a global mean sea level. Over the last few decades of the satellite era, the relative rates of rises have changed in these locations somewhere in positive, and somewhere else in negative, for an average relative sea level acceleration very close to zero. This is the most relevant result for climate change monitoring.
5. Analysis of the Fremantle Tide Gauge
In case of Fremantle, data from [13], analysis in Figure 5, the likely subsidence of the tide gauge is about -1.73 mm/year pretty much the same since the start of the recording.
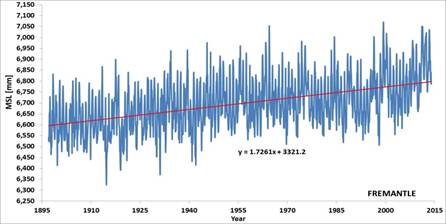
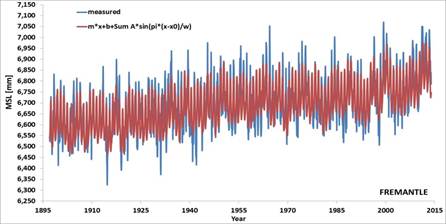
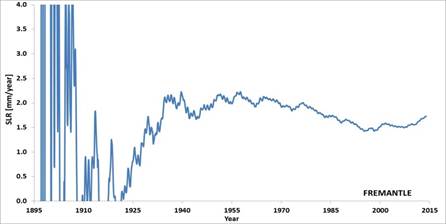
Figure 5. Monthly average relative mean sea levels measured by the Fremantle tide gauge, with linear and linear plus multiple sinusoidal fittings, and relative rate of rise by linear fitting all the data collected up to a given time (data from [13]).
In the picture there are oscillations about the line of slope +1.73 mm/year of known periodicities from inter-annual to quasi-60 years multi-decadal. The figure also presents the different slopes computed at different times from the opening of the tide gauge. Before 1957, the multi-decadal oscillations, especially the quasi-60 years, do not permit to infer any reasonable trend. After 1957, the estimation starts to become accurate. After 1977, the slope (i.e. the relative rate of rise of sea levels) is then minimally reducing till the mid-2000s. Then, it is marginally increasing. This is the effect only of the decadal and multi-decadal oscillations. Since 1977, the relative sea level rise at the tide gauge has been variable between -1.99 and -1.45 mm/year. This variation has certainly not been the result of a variable subsidence between -2 and -4 mm/year of the tide gauge instrument that is nowhere to be seen. As the sea levels are oscillating about the same long term trend since many decades, either the subsidence of the tide gauge than the contribution by mass addition and thermal expansion to sea level rise are very likely constant.
6. Conclusion
The search for absolute sea level rises only hides the lack of any acceleration in the relative sea level rises that permits to indirectly challenge the claims of significant mass additions from melting of ices on land and thermal expansion from warming of oceans.
There is no trace of non-linear subsidence in the Fremantle tide gauge with rates of -2 to -4 mm/year. Rather, there are natural oscillations of the relative sea levels with detectable periodicities up to a quasi-60 years about a possible constant subsidence rate of -1.7 mm/year.
We may conclude that the Fremantle tide gauge is not experiencing any accelerating land subsidence, not any accelerating relative rise of the seas.
Appendix
Table A1. Table of the relative rates of rise of the 108 worldwide tide gauges in the PSMSL data base with more than 80 years of recording.
| Years of data | Start | End | Trend [mm/year] | Error [mm/year] | tide gauge |
| 188 | 1807 | 2013 | 1.05 | 0.1 | BREST |
| 183 | 1811 | 1999 | 0.8 | 0.08 | SWINOUJSCIE |
| 168 | 1843 | 2010 | 2.53 | 0.13 | CUXHAVEN 2 |
| 166 | 1848 | 2013 | 1.66 | 0.09 | MAASSLUIS |
| 165 | 1849 | 2013 | 1.43 | 0.06 | WISMAR 2 |
| 159 | 1855 | 2013 | 1.38 | 0.16 | SAN FRANCISCO |
| 158 | 1856 | 2013 | 1.26 | 0.07 | WARNEMUNDE 2 |
| 152 | 1862 | 2013 | 1.23 | 0.36 | VLISSINGEN |
| 150 | 1856 | 2013 | 1.65 | 0.06 | TRAVEMUNDE |
| 150 | 1864 | 2013 | 2.39 | 0.08 | HOEK VAN HOLLAND |
| 149 | 1865 | 2013 | 1.47 | 0.08 | DEN HELDER |
| 149 | 1865 | 2013 | 1.68 | 0.12 | DELFZIJL |
| 149 | 1865 | 2013 | 1.38 | 0.09 | HARLINGEN |
| 143 | 1856 | 2013 | 2.82 | 0.09 | NEW YORK ( THE BATTERY) |
| 142 | 1872 | 2013 | 1.47 | 0.3 | IJMUIDEN |
| 135 | 1879 | 2013 | -2.28 | 0.17 | HELSINKI |
| 134 | 1874 | 2013 | 6.75 | 0.24 | POTI |
| 129 | 1884 | 2013 | -7.27 | 0.17 | VAASA / VASA |
| 127 | 1887 | 2013 | -1.09 | 0.14 | OLANDS NORRAUDDE |
| 127 | 1887 | 2013 | 0.03 | 0.12 | KUNGSHOLMSFORT |
| 125 | 1889 | 2013 | -3.79 | 0.16 | STOCKHOLM |
| 125 | 1889 | 2013 | -6.33 | 0.2 | OULU / ULEABORG |
| 124 | 1885 | 2013 | 1.29 | 0.13 | MARSEILLE |
| 124 | 1889 | 2012 | 1.24 | 0.14 | ESBJERG |
| 123 | 1878 | 2010 | 0.83 | 0.18 | MUMBAI / BOMBAY (APOLLO BANDAR) |
| 123 | 1889 | 2012 | 0.61 | 0.09 | AARHUS |
| 123 | 1890 | 2012 | 1.09 | 0.08 | FREDERICIA |
| 122 | 1892 | 2013 | -7.75 | 0.19 | RATAN |
| 122 | 1891 | 2012 | 0.4 | 0.15 | HORNBAEK |
| 121 | 1892 | 2012 | 1.19 | 0.1 | GEDSER |
| 121 | 1875 | 2013 | 1.26 | 0.1 | TRIESTE |
| 120 | 1892 | 2012 | -0.22 | 0.12 | HIRTSHALS |
| 119 | 1887 | 2005 | -2.91 | 0.16 | LANDSORT |
| 117 | 1889 | 2013 | -2.63 | 0.18 | HANKO / HANGO |
| 116 | 1897 | 2012 | 0.84 | 0.1 | KORSOR |
| 115 | 1896 | 2012 | 1.04 | 0.1 | SLIPSHAVN |
| 115 | 1899 | 2013 | 1.95 | 0.12 | SEATTLE |
| 113 | 1901 | 2013 | 2.91 | 0.18 | PHILADELPHIA (PIER 9N) |
| 112 | 1896 | 2013 | 1.88 | 0.12 | NORTH SHIELDS |
| 112 | 1897 | 2013 | 1.72 | 0.19 | FREMANTLE |
| 111 | 1903 | 2013 | 3.15 | 0.14 | BALTIMORE |
| 109 | 1905 | 2013 | 1.41 | 0.13 | HONOLULU |
| 108 | 1886 | 1993 | 0.6 | 0.18 | SYDNEY, FORT DENISON |
| 108 | 1906 | 2013 | 2.04 | 0.11 | SAN DIEGO (QUARANTINE STATION) |
| 106 | 1882 | 1993 | 1.26 | 0.19 | CASCAIS |
| 106 | 1908 | 2013 | 1.49 | 0.17 | BALBOA |
| 105 | 1898 | 2011 | 1.48 | 0.25 | KLAIPEDA |
| 105 | 1909 | 2013 | 6.35 | 0.19 | GALVESTON II, PIER21, TX |
| 104 | 1862 | 1965 | 0.45 | 0.22 | ABERDEEN II |
| 104 | 1886 | 2013 | -2.96 | 0.34 | OSLO |
| 104 | 1910 | 2013 | 0.59 | 0.16 | VICTORIA |
| 103 | 1898 | 2013 | 2.03 | 0.1 | FERNANDINA BEACH |
| 103 | 1911 | 2013 | -5.85 | 0.24 | MANTYLUOTO |
| 103 | 1911 | 2013 | -1.83 | 0.17 | SMOGEN |
| 102 | 1869 | 1970 | -3.44 | 0.19 | NEDRE SODERTALJE |
| 102 | 1912 | 2013 | 1.9 | 0.19 | PORTLAND (MAINE) |
| 101 | 1913 | 2013 | 2.3 | 0.13 | KEY WEST |
| 99 | 1912 | 2013 | 4.08 | 0.16 | ATLANTIC CITY |
| 99 | 1915 | 2013 | -7.18 | 0.28 | PIETARSAARI/JAKOBSTAD |
| 98 | 1915 | 2013 | 0.96 | 0.15 | SYDNEY, FORT DENISON 2 |
| 98 | 1916 | 2013 | 1.79 | 0.12 | NEWLYN |
| 98 | 1916 | 2013 | -8.06 | 0.28 | FURUOGRUND |
| 98 | 1916 | 2013 | -1.15 | 0.22 | VISBY |
| 96 | 1916 | 2013 | -0.11 | 0.22 | BERGEN |
| 96 | 1917 | 2012 | 2.38 | 0.28 | TUAPSE |
| 95 | 1887 | 1981 | 0.61 | 0.16 | YSTAD |
| 95 | 1887 | 1981 | -0.86 | 0.16 | VARBERG |
| 95 | 1896 | 2011 | 3.04 | 0.17 | HALIFAX |
| 95 | 1919 | 2013 | -0.3 | 0.16 | KETCHIKAN |
| 94 | 1904 | 1998 | 1.26 | 0.17 | AUCKLAND II |
| 94 | 1920 | 2013 | -6.88 | 0.31 | KEMI |
| 93 | 1921 | 2013 | 2.8 | 0.24 | BOSTON |
| 93 | 1921 | 2013 | 1.06 | 0.23 | WEST-TERSCHELLING |
| 92 | 1922 | 2013 | 3.12 | 0.21 | CHARLESTON I |
| 92 | 1922 | 2013 | -3.59 | 0.3 | TURKU / ABO |
| 91 | 1884 | 1996 | 1.2 | 0.07 | GENOVA |
| 91 | 1896 | 1986 | -6.03 | 0.25 | NEDRE GAVLE |
| 90 | 1923 | 2013 | -6.77 | 0.32 | RAAHE / BRAHESTAD |
| 90 | 1924 | 2013 | 0.83 | 0.15 | LOS ANGELES |
| 89 | 1925 | 2013 | -0.88 | 2.21 | TROIS-RIVIERES |
| 89 | 1909 | 2013 | 1.08 | 0.17 | PRINCE RUPERT |
| 89 | 1909 | 2000 | 2.47 | 0.26 | VENEZIA (PUNTA DELLA SALUTE) |
| 89 | 1925 | 2013 | -0.35 | 0.24 | ASTORIA (TONGUE POINT) |
| 88 | 1919 | 2013 | 0.46 | 0.19 | STAVANGER |
| 88 | 1894 | 1983 | 0.33 | 0.27 | TONOURA |
| 88 | 1924 | 2011 | 2.15 | 0.2 | PENSACOLA |
| 88 | 1924 | 2013 | -3.68 | 0.29 | FOGLO / DEGERBY |
| 87 | 1927 | 2013 | -6.38 | 0.33 | KASKINEN / KASKO |
| 86 | 1925 | 2013 | 2.04 | 0.15 | LA JOLLA (SCRIP PS PIER) |
| 86 | 1928 | 2013 | 4.59 | 0.21 | SEWELLS POINT, HAMPTON ROADS\ |
| 86 | 1928 | 2013 | 0.24 | 0.14 | TREGDE |
| 86 | 1928 | 2013 | -1.45 | 0.23 | HEIMSJO |
| 85 | 1892 | 1976 | -6.12 | 0.27 | BJORN |
| 85 | 1929 | 2013 | -0.85 | 0.38 | HAMINA |
| 84 | 1910 | 2013 | -1.69 | 0.21 | TOFINO |
| 84 | 1930 | 2013 | 2.21 | 0.27 | EASTPORT |
| 83 | 1910 | 1994 | 1.26 | 0.39 | SEVASTOPOL |
| 83 | 1930 | 2013 | -0.21 | 0.35 | HOSOJIMA |
| 83 | 1911 | 2011 | 0.1 | 0.36 | QUEBEC (LAUZON) |
| 83 | 1929 | 2013 | 3.54 | 0.2 | ANNAPOLIS (NAVAL ACCADEMY) |
| 83 | 1930 | 2013 | 0.57 | 0.21 | KLAGSHAMN |
| 83 | 1931 | 2013 | 2.72 | 0.18 | NEWPORT |
| 83 | 1931 | 2013 | 3.14 | 0.24 | WASHINGTON DC |
| 82 | 1930 | 2013 | -0.06 | 0.3 | WAJIMA |
| 82 | 1905 | 1987 | 1.52 | 0.32 | BUENOS AIRES |
| 81 | 1930 | 2013 | 3.71 | 0.21 | ABURATSUBO |
| 81 | 1933 | 2013 | 4.05 | 0.21 | SANDY HOOK |
| 81 | 1933 | 2013 | -4.52 | 0.36 | RAUMA / RAUMO |
| 80 | 1933 | 2013 | 2.79 | 0.21 | WOODS HOLE (OCEAN.INST.) |
| 108.5 | 0.191835 | 0.21 | average | ||
| 188 | 6.75 | maximum | |||
| 80 | -8.06 | Minimum | |||
References
- www.psmsl.org/products/trends
- Parker, A., M. Saad Saleem and M. Lawson (2013), Sea-Level Trend Analysis for Coastal Management, Ocean and Coastal Management. Ocean & Coastal Management, 73:63–81.
- N-A Mörner and A. Parker (2013), Present-to-future sea level changes: The Australian case,Environmental Sciences: An Indian Journal, 8(2):43-51.
- Parker, A. (2013), MINIMUM 60 YEARS OF RECORDING ARE NEEDED TO COMPUTE THE SEA LEVEL RATE OF RISE IN THE WESTERN SOUTH PACIFIC, Nonlinear Engineering. 3(1): 1–10.
- Parker, A. (2014), Confirming the lack of any sea level acceleration around the Australian coastline, Nonlinear Engineering Nonlinear Engineering. 3(2): 99–105.
- A. Parker (2014), Accuracy and Reliability Issues in the Use of Global Positioning System and Satellite Altimetry to Infer the Absolute Sea Level Rise, Journal of Satellite Oceanography and Meteorology, 1(1):13-23.
- www.sonel.org/spip.php?page=gps&idStation=812
- sideshow.jpl.nasa.gov/post/links/PERT.html
- sealevel.colorado.edu/content/map-sea-level-trends
- W. E. Featherstone, N. T. Penna, M. S. Filmer and D. P. Williams (2015), Nonlinear subsidence at Fremantle, a long-recording tide gauge in the Southern Hemisphere, Journal of Geophysical Research: Oceans,DOI: 10.1002/2015JC011295.
- www.sonel.org/spip.php?page=gps&idStation=1918
- www.sonel.org/-Sea-level-trends-.html?lang=en
- www.psmsl.org/data/obtaining/stations/111.php



