Mathematical Model of Dangerous Changing the Groundwater Level in Ukrainian Industrial Cities
Elena Serikova1, *, Elena Strelnikova1, Valery Yakovlev2
1A. N. Podgorny Institute for Mechanical Engineering Problems of the National Academy of Sciences of Ukraine, vul. Pozharskoho 2/10, Kharkiv, Ukraine
2Geological Company "Sherl" Ltd., vul. Kirova, Kharkiv, Ukraine
Abstract
Paper treats the issue concerned with drastic increasing the groundwater level through the influence of technogenic factors of urban environment. Data of perennial climate research and estimation of additional groundwater replenishment of Ukraine territory have been employed in the paper. Emphasis is on mathematical modeling of groundwater level changing over the time for different limited areas of urban territory. The forecast of groundwater level changing for typical industrial Ukrainian city for the next 50 years has been provided. Measures to optimize the water balance in critical zones of industrial cities have been determined.
Keywords
Mathematical Modeling, Flooding, Groundwater Level, Water Balance, Additional Groundwater Replenishment
Received: April 8, 2015 / Accepted: April 27, 2015 / Published online: May 15, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
Most objects of the Ukraine water supply system are in a poor technical condition. Leakages from water supply systems, sewerage systems and from thermal networks in some regions have already reached 40-50 percent of water supply volume. Leakages from water communications lead to flooding and change qualitative composition of groundwater. In the industrial cities of Ukraine additional groundwater replenishment is many times greater than the natural infiltration of precipitation [6]. For example, for Kharkiv city the additional groundwater replenishment was 210 000 thousand m3/year (575 300 m3/day) in the period 2005-2014 years [2,6]. Compensation of additional groundwater replenishment volume due to water abstraction for drinking and technical needs does not usually occur because of poor water quality of shallow horizons. Total water abstraction from the first of surface aquifer in the period 2005-2014 years is averaging 19700 m3/day for Kharkiv. This difference in credit and debit water balance technogenic components is compensated by transpiration only when the ground water level closed to surface, i.e. in concrete flooded conditions [7].
Flooding processes currently do not have adequate expression by mathematical modeling. The issue of forecast has been solved by Averyanov, Muftahov, Sologaev, Polubarinova-Kochina, Verigin, Telima, Kremez etc. in incomplete statements, in different cases excluding additional groundwater replenishment, dependency of time, transpiration and evaporation [3,4,10].
2. Materials and Methods
On the example of Kharkiv, typical industrial city of Ukraine, the mathematical model has been developed for the groundwater regime prediction including the change of water management conditions. Developed model considers all important water balance components, such as, natural infiltration of precipitation, additional groundwater replenishment, transpiration, evaporation and water abstraction.
The case of plane filtering has been considered in the paper. There are artificial pavements and buildings occupied a large area of big cities territory including Kharkiv territory, which prevents the natural processes of precipitation infiltration, evaporation and transpiration. Therefore, the plot of territory partially covered by artificial turf will be considered in modeling of groundwater level changing. The impact of natural and technogenic factors will be occurred only on the free surface of this plot. The scheme of groundwater level changing has been presented on the Figure 1.
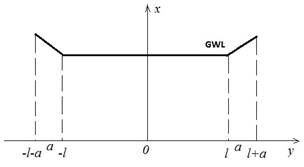
Figure 1. The scheme of groundwater level changing. Side view.
The influence of natural and technogenic factors to groundwater level changing are took place on the plots [-l-a÷-l] and [l÷l+a]; on plots [-l ÷ 0] and [0 ÷ l] there are no impact on the groundwater level due to the pavement [8].
Equation of pressure filtration has the form
![]() , (1)
, (1)
where h- groundwater level, x,y – coordinates shown on the Figure 1., γ – coefficient of anisotropy.
Since the groundwater level changing and its distribution is local and simulation performs for limited areas of urban territory (industrial objects, buildings, etc.) with homogeneous hydrogeological conditions, it can be assumed that the lateral inflow and outflow are equal, so
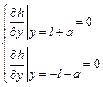 .
.
The initial level has been taken as the starting point, h=0
![]() .
.
Infiltration, water intake, transpiration and evaporation are assumed not to be on the plots –l ÷0 and 0÷l because of artificial turf.
![]() .
.
Infiltration, water intake, transpiration and evaporation are take place on the plots [-l-a÷-l] and [l÷l+a]
![]() ,
,
where f1 – additional groundwater replenishment (the credit of groundwater balance); s1 – rainfall to infiltrate in groundwaters (the credit of groundwater balance); g1 – transpiration rate (the debit of groundwater balance); d1 – evaporation rate (the debit of groundwater balance); k1 – water intake from groundwater (the debit of groundwater balance). The similar condition has been implemented on the plot [-l-a÷-l], marking the corresponding parameters of the water balance by index 2.
Create a symmetric model, so f1= f2; s1= s2; g1= g2; d1= d2; k1= k2.
Obtained
![]() .
.
The mathematical model is described by a boundary value issue for a non-stationary differential equation of filtration pressure. The solution of the boundary value problem is obtained in the form [8]:
![]() (2)
(2)
where h – groundwater level; [- l, l]- considered plot of territory, where transpiration and evaporation are took place from l to l+a; γ – coefficient of anisotropy; Dn,mn – coefficients which are determined by the technogenic impacts.
Denoting![]() , than
, than
![]() ;
; ![]() ,
,
The following equation was obtained for identifying these unknown coefficients
![]() (3)
(3)
Bellow we identify the coefficients. Because of symmetric case that has been considered, dot product of (3) by the function![]() , will have
, will have
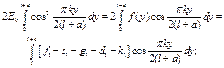
![]() ,
,
As a result of calculating these factors, will be finding the value of Е1, Е2, Е3.
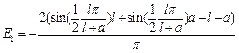 ,
,
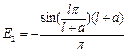 ,
,
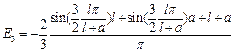 .
.
Numerical analysis has been shown that three members of a series are sufficient to ensure the accuracy of the solution e=10-3 [8].
Calculations and visualization of the modeling for the Kharkiv city territory were implemented by the software package Maple.
The following values of water balance components have been adopted for calculations.
The average long-term groundwater replenishement according lysimetric research of station "Feofania" in village Khotov of Kiev region with a total annual rainfall of 560mm/year, is 1,5 • 10-4 m/day.
The amount of rainfall to infiltrates into groundwater s1=1,5•10-4 m/day.
Coefficients g1 and d1 are calculated according to the formulas [5,9].
Transpiration rate g1=0,15÷1,47g/dm2•h=6,25•10-8kg/m2•day
Evaporation rate d1 = 0,21g/dm2•h =8,75•10-8 kg/m2•day
Anisotropy factor g =1.
Let T - relative transpiration, T = 0,7 ÷ 0,85, and it can be calculated by the formula
![]()
where, It - transpiration rate (g1).
Ie - evaporation rate (d1) [5,9].
The value of additional groundwater replenishment is supposed to be equal
f1=210000thousand m3/year = 0,7 m/year = 1,9 • 10-3 m/day.
The value of water abstraction from groundwater is equals to
k1=19743m3/day = 6,6•10-5m/day [8].
3. Conclusions and Discussion
Vizualization of calculations for the industrial Kharkiv city territory has been presented on the Figure 2. The function h(x,y), calculated by the formula (1) has been shown.
Groundwater level changing on Δh0 = 0,00007 m per day has been presented on a graph.
The forecast based on calculations of groundwater level changing of Kharkiv for the next 50 years has been provided in the paper.
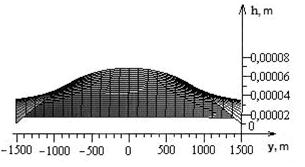
Figure 2. Groundwater level changing. Frontal image.
The groundwater level will be increased to average 0,03 m on the 1st year and 1,5 m on the 50th year.
Flooding factors ranking on the impact significance has been presented in the Table 1.
Because of technogenic factors having 1st and 3d rank and are subjected to significant changes, 5 variants of possibly influence of technogenic factors on groundwater level will be simulated. It corresponds to variation statistics methods [1]. In this case, the significance of the impact of additional groundwater replenishment to the water balance will be reduced of 10% in each of the following case and will be increased the significance of the impact of water intake on 10%. It will be so, until water intake value will exceed additional groundwater replenishment.
The significance of the impact technogenic factors on the groundwater level of the Kharkiv territory has been presented in the Table 2.
Table 1. Flooding factors ranking on the impact significance.
| Factors ranking on the impact significance | Name of groundwater impact factor | Lettering impact factor | The numerical value, m/day | Value in % |
| 1 | Additional groundwater replenishment | f1 | 1,9·10-3 | 89,786 |
| 2 | Precipitation to infiltrate in groundwater | s1 | 1,5·10-4 | 7,088 |
| 3 | Water intake | k1 | 6,6·10-5 | 3,119 |
| 4 | Evaporation rate | d1 | 8,75·10-8 | 0,004 |
| 5 | Transpiration rate | g1 | 6,25·10-8 | 0,003 |
Table 2. The significance of the impact technogenic factors on the groundwater level of the Kharkiv territory.
| № | Name of groundwater impact factor | Actual value in % | 1 variant, % | 2 variant, % | 3 variant, % | 4 variant, % | 5 variant, % |
| 1 | Additional groundwater replenishment | 89,786 | 79,786 | 69,786 | 59,786 | 49,786 | 39,786 |
| 2 | Water intake | 3,119 | 13,119 | 23,119 | 33,119 | 43,119 | 53,119 |
Table 3. The significance of the different impact technogenic factors on groundwater balance in Kharkiv.
| № | Name of groundwater impact factor | The numerical value, m/day | 1 variant, m/day | 2 variant, m/day | 3 variant, m/day | 4 variant, m/day | 5 variant, m/day |
| 1 | Additional groundwater replenishment | 1,9·10-3 | 1,7·10-3 | 1,5·10-3 | 1,3·10-3 | 1,1·10-3 | 0,8·10-3 |
| 2 | Water intake | 6,6·10-5 | 2,8·10-4 | 4,9·10-4 | 0,7·10-3 | 0,9·10-3 | 1,1·10-3 |
| Δh | 0,00007 | 0,000065 | 0,000054 | 0,000033 | 0,000021 | 0,000012 | |
Table 4. The forecast of groundwater level changing on Kharkiv territory for different time periods.
| Time interval | Day | 1 year | 10 years | 20 years | 30 years | 40 years | 50 years | |
| Groundwater level changing | ||||||||
| Background situation | Δh0 | 0,00007 m | 0,030 m | 0,3 m | 0,6 m | 0,9 m | 1,2 m | 1,5 m |
| 1 variant | Δh1 | 0,000065 m | 0,024 m | 0,24 m | 0,48 m | 0,72 m | 0,96 m | 1,2 m |
| 2 variant | Δh2 | 0,000054 m | 0,020 m | 0,2 m | 0,4 m | 0,6 m | 0,8 m | 1,0 m |
| 3 variant | Δh3 | 0,000033 m | 0,012 m | 0,12 m | 0,24 m | 0,36 m | 0,48 m | 0,6 m |
| 4 variant | Δh4 | 0,000021 m | 0,008 m | 0,08 m | 0,16 m | 0,24 m | 0,32 m | 0,4 m |
| 5 variant | Δh5 | 0,000012 m | 0,004 m | 0,04 m | 0,08 m | 0,12 m | 0,16 m | 0,2 m |
The significance of the different impact technogenic factors on groundwater balance in Kharkiv has been presented in the Table 3.
Visualization the possible situation of groundwater level changing on the Kharkiv territory including optimization of water balance components, where water intake volume exceed the additional groundwater replenishment, has been presented on the Figure 3.
Groundwater level changing on Δh0 = 0,000012 m per day has been presented on a graph. Modeling situation where water intake volume exceed the additional groundwater replenishment, has been simulated. In this case the groundwater level will be increased to average 0, 004 m on the 1st year and 0,2 m on the 50th year.
Simulated situation shows that groundwater level increasing less in 7,5 times than in real conditions (figure 2).
The forecast of groundwater level changing on Kharkiv territory for different time periods has been presented in the table 4.
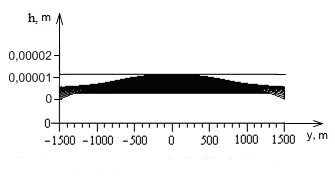
Figure 3. Groundwater level changing with concrete parameters m per day. Frontal image.
Results processing has been carried out via the variation statistic method. Test outcomes have been presented graphically and in tables. Six cases of technogenic factors impacting on groundwater level have been considered. The coefficient of variation was 26,5%. Aggregate of numbers under treating can be homogeneous, because the coefficient of variation was less than 33% [1].
Developed model presented two ways of water balancing of debit and credit water balance components for the period 2005-2014 years. They are decreasing additional groundwater replenishment in 2,4 times, i.e. additional groundwater replenishment must be reduced by an average of 240,000 m3/day and increasing of water intake from the first of surface aquifer in 15 times, i.e. increase the average water intake of 300 000 m3/day. The sum of these amounts of water is 540 000 m3/day. Because of bad conditions of groundwater at Kharkiv, waters to intake could be used for technical purposes. For example washing roads, pavements, automobiles, making skating rinks, watering plants, in construction, in industrial water-cooling and water-thermal systems, for firefighting have been proposed.
In the future treatment will be provided to prevent the economic damage of urban area flooding and a typical optimization program of complex measures for flooding prevention will be developed.
References
- Chernova N.I., 2007. Mathematical Statistics: tutorial. Novosibirsk State University, Novosibirsk. 148pp
- Howard,K.W.F.,2007. Urban Groundwater – Meeting the ChallengeIAH-SP Series, Volume 8.Taylor & Francis.Howard,K.W.F. (Ed.), 307рp.
- Kremez V. S., Buts Y. V., Tsymbal V. A., 2003. Actual issues of modeling flooding territories and other dangerous processes concerned with groundwater regime changes. In: Mitropolsky O. (Ed.): Environmental Ecology and Life Safety №6, Kiev, pp.56-64.
- Pshinko A.N., Belyaev N.N., Pokutneva L.V., 2008. Numerical modeling of flooding process. In: MyamlinS.V.(Ed.): Bulletin of Dnepropetrovsk National University of Railway Transport named after Academician V. Lazaryan №25, Dnepropetrovsk, pp.84-87.
- Rubin B.A., 1971. Course of Plant Physiology, 3rd ed., Moskow, 672 pp.
- Serikova E.N., Yakovlev V.V., 2011. Additional infiltration to underground waters of big cities territory (on example Kharkiv region). In: Babaev V.N. (Ed.): Proc.: Municipal Economy of Cities №97, Kharkiv, KNAME. pp. 344-348.
- Serikova E.N., Strelnikova E.A., 2013. The treatment of characteristics of groundwater level changing via the mathematical modeling. In: Filippenko I.G. (Ed.): Eastern-European Jornal of Enterprise Technologies №3/4, Kharkiv, pp. 31-35.
- Serikova E.N., Strelnikova E.A., Yakovlev V.V., 2014. Mathematical modeling of groundwater level changing in cities taking lead factors of the water balance. In: Bardachov Y.M. (Ed.): Bulletin of Kherson National Technical University №4 (51), Kherson, pp. 182-191.
- Sleycher R., 1970. Water regime of plants, Moscow: Mir. 368pp.
- Telima S.V., Revyakina N.Y., 2011. Model research processes of flooding by groundwater of urban areas in modern conditions. In: Voloshkina O.S., Trofimchuk O.M. (Eds.): Proc.: Environmental Safety and Nature Resources №7, Kiev, pp. 45-63.



