Dark Exciton Mass Spectrum with Relativistic Correction
Arezu Jahanshir*
Department of Eng. Science, Buein Zahra Technical University, Qazvin, Iran
Abstract
Characteristics and properties of exotic exciton systems (EXS) are often different and have too many opportunities for applications. Here we investigate one of the properties of dark exotic exciton system in the semiconductors. Interactions in semiconductors should be defined in relativistic and quantum limits. Thus, based on relativistic effects, we should describe all physical parameters like mass, binding energy, spin-orbital interactions etc. In this paper, we studied dark exciton. Based on the investigation of asymptotic behavior of the loop function for the charged scalar particles in the external gauge field, and have been able to obtain the mass spectrum of bound state and the constituent mass of dark exciton system. It shows that the mass of particles is different in bound and free states. We have found out that determining the mass of the bound state systems requires; first of all, determine the eigenvalue of the Hamiltonian with Coulomb potential and then calculating the mass and binding energy of dark exciton which we could be achieved. This method can be applied to calculate necessary parameters for exotic systems. Therefore, the presented equations are the appropriate method for investigating all bounding system in which we can analyze changes in energy and mass spectrum using intended potentials. Therefore, dark exciton binding energy is investigated by considering quantum filed theories. The results are compared in ground states and excited states that are very important in modern nanostructures like quantum dots, quantum wells and modern part of theoretical spintronics subjects.
Keywords
Binding Energy, Bound State, Exotic System, Loop Function, Nanophysics
Received: August 13, 2015
Accepted: September 5, 2015
Published online: September 17, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
In semiconductor quantum dots which are smaller than the bulk exciton Bohr radius, the energy spectrum of electron-hole pairs can be approximated using the independent quantization of the electron and hole motion. In the case of quantum dots this leads to the condition of bounding states. Recently, the wide exotic systems in semiconductors have attracted much attention due to their potential applications in spintronics ultra quantum technology and devices. Nowadays these exotic systems named after exciton, dark exciton, bright exciton, light exciton, exciton-polariton, etc. Among them, dark exciton for different optoelectronic characteristics and applications has been proposed as new wide exotic system in semiconductors theories. Dark EXS structure because of optical effects and spins interaction has several advantages compared to light EXS [1]. The results suggest that an understanding of the role of relativistic corrections in EXSs is very important and interesting in order to give us to investigate the new quanto-optical properties. There have been several theoretical studies on EXS binding energy in semiconductors. We investigated the relativistic effects on the exciton binding energies of the heavy exciton bound system. We found that, due to the quantum effects, the binding energies of EXS in semiconductors dependent on some of the quanto-relativistic parameters that are described by electromagnetic field theory and the form of potential interaction. On the other hand, many fundamental excitonic effects can very well understand by using QFT [2, 3], because QFT theories based on QM and they are in the high development stage [2-4]. In this article, we described the EXS binding energies of the ground and excited states and proposed one of the versions of calculation of the mass spectrum and binding energy of EXS in the framework of the basis investigation of the asymptotically behavior of the loop function of charged scalar’s particles in the external electromagnet field. Theoretically and analytically are determined explorations of these states through relativistic corrections. It shows that, the mass and binding energy of dark EXS based on relativistic correction and solving method of Schrödinger equation, increases with increasing constant of interactions in different energy levels. Actually, we will determine the reduced mass and the constituent mass inside the bound states system of exotic dark exciton. In this letter, the physical parameters for EXS with the electron effective mass for a series of (In, Ga)As/GaAs single quantum well are obtained by using QFT and QM models. The electron effective mass in the InxGayAs|GaAs increase in the range of0.049±0.007me to 0.11±0.015me, so our calculation based on 0.049±0.007me ,the heavy hole effective mass 0.457±0.043me and the electron mass me=0.510998910MeV.
2. Theoretical Model
In the EXSs, the free electron and hole states interact through the screened Coulomb interaction to form. For small exotic conjugated particles, the exciton binding energy can be calculated treating exciton as bounding states that have interacted by a simple spherical-symmetric Coulomb potential
![]()
where ε, ε0 are the dielectric constant and r is the equivalent radius of the exciton system. Determinations of quanto-relativistic characteristics of EXS are important for understanding electron-hole transport levels and spins interactions that effect on the binding energy and mass spectrum in EXS. These effects give rise to define the total Hamiltonian interactions in EXS that is necessary to calculate the binding energy and mass spectrum of EXS. In order to define corrections for physical parameters in EXS we used systematically the theoretical theories, so that definition can be done for any new exotic systems in semiconductors. Though the model overlooks the EXS in semiconductors likes the bound state system with two charged particles and electrostatics interactions. In particular this model is suitable for developing all exotic bounding systems with contain two particles, particle-semiparticle and for hadronic atoms in particle physics. We would like to point out here that, these calculated parameters shown correlation with experimentally determined energy levels by other methods. The method based on many-body characteristic in QFT and QED representation that describe relativistic and nonrelativistic characteristics of bounding systems, and this model require to solve the Schrödinger equation with QFT, QED and QM methods in the interaction between charged particles that have bounding connections [5-8]. The characteristics of EXS present by the asymptotic behavior of the polarization loop function for a charged particles in the external field:
![]() (1)
(1)
As we can describe the loop function effect in interaction, so the mass and the energy spectrum of EXS theoretically could be determined. Therefore, in one need to find the Green’s function for this field [5-7] by averaging over the field as follow
![]() (2)
(2)
and consider only the lowest order or only the two-point Gauss correlator. The result will be shown in the functional integral that likes to the Feynman path integral for the motion of particles with different masses [8-12] i.e. the heavy hole and an electron in dark exotic exciton systems:
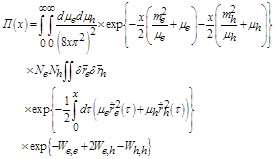 (3)
(3)
Thus, in the equation (3) the total interaction has been presented by potential (Wii) and nonpotential (Wij) interactions. Interaction of heavy hole and electron (![]() ) is described by the nonlocal functional by the last exponential part of equation (3). In other words, nonpotential interactions describe action and portion of particles mass in eigenenergy;
) is described by the nonlocal functional by the last exponential part of equation (3). In other words, nonpotential interactions describe action and portion of particles mass in eigenenergy; ![]() are potential interactions between particles [13, 14]. Using some mathematical modifications in the infinite limit for solving equation (3), we can determine mechanism of interactions and creation of bound state [15]. Thus the mass of the bound state will defined as:
are potential interactions between particles [13, 14]. Using some mathematical modifications in the infinite limit for solving equation (3), we can determine mechanism of interactions and creation of bound state [15]. Thus the mass of the bound state will defined as:
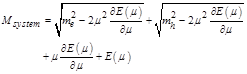 (4)
(4)
where the parameter m is determined from the equation:
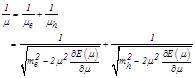 (5)
(5)
where
![]() (6)
(6)
The parameter![]() is the constituent mass of particles in the EXS bound state,
is the constituent mass of particles in the EXS bound state, ![]() is the eigenvalue of the relativistic Hamiltonian and it depend on the reduced mass
is the eigenvalue of the relativistic Hamiltonian and it depend on the reduced mass![]() of the EXS bound state and the coupling constant, and
of the EXS bound state and the coupling constant, and ![]() are the electron and heavy hole masses in a free state. As the bound hole and electron pair is confined to the excitonic system. Evidences support that EXS behave similarly like atomic system, therefore, the binding energy can be written as atomic energy. Now let us to determine the EXS binding energy of exotic system with masses
are the electron and heavy hole masses in a free state. As the bound hole and electron pair is confined to the excitonic system. Evidences support that EXS behave similarly like atomic system, therefore, the binding energy can be written as atomic energy. Now let us to determine the EXS binding energy of exotic system with masses![]() [15-17] In this case for the binding energy or the bound state energy from atomic and nuclear physics with this well-known equation [18, 19]:
[15-17] In this case for the binding energy or the bound state energy from atomic and nuclear physics with this well-known equation [18, 19]:
![]() (7)
(7)
From equation (6) we can see that for finding the binding energy equation and its relation to the other physical parameters in the bound state systems, we shall determine the eigenvalues of the total Hamiltonian with Coulomb potential. For this aim we consider following Schrödinger equation:
![]() (8)
(8)
From this equation we find the energy spectrum of Coulomb potential for heavy EXS in the (In0.4 Ga0.6As|GaAs) where the heavy hole effective mass is 0.457me and the electron effective mass is 0.049me. During our calculations we consider that the effective mass of heavy hole in the dark exciton system is much more than the effective mass of electron. So, analytically determination value base on the heavy hole mass. Therefore, we obtained the theoretically equation for binding energy, the mass spectrum and the constituent mass of dark exotic exciton system that presented in below equations [14-17]:
![]() (9)
(9)
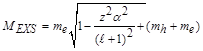 (10)
(10)
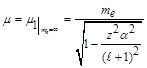 (11)
(11)
where ![]() is the coupling constant of electromagnetic interaction and
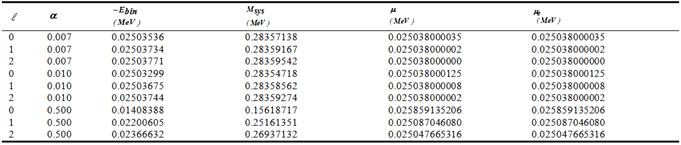
is the coupling constant of electromagnetic interaction and ![]() is the orbital quantum number. The calculation results are given in table 1 (at the end of article). It is showing that the constituent mass will decrease with growth of the coupling constant and dark exciton system could be more stable with a good long lifetime values.
is the orbital quantum number. The calculation results are given in table 1 (at the end of article). It is showing that the constituent mass will decrease with growth of the coupling constant and dark exciton system could be more stable with a good long lifetime values.
Table 1. Binding energy, mass spectrum, constituents (![]() ) and reduced mass of particle in the dark EXS.
) and reduced mass of particle in the dark EXS.
3. Conclusion
Great efforts have been made to understand how bound state arise in the formalism of quantum field theory and to work out effective methods to determine the mass and characteristics of these bound states, especially binding energy. The analysis of a bound state is simplest when constituent particles travel at speeds considerably less than light. The coupling constant should be weak and masses of intermediate particles should be small in comparison with masses of constituents. New importance to the bound state physics was given by the development of QCD, the modern theory of strong interactions or electromagnetic interactions, which have constant of interactions near to strong interactions. Now the technical achievements of experimental studies make it possible to obtain the bounding systems with constant of interaction that reach to the order of one, so that electromagnetic interactions become strong and the calculation of relativistic corrections becomes necessary. We will consider this problem, according to the asymptotic behavior of the loop function in the scalar electrodynamics field and use the oscillator representation method. The OR method based on the free field representation of Hamiltonian for the system. The Russian theoretic Efimov G.V explicitly formulated it in 1989. We show that normal and exotic bound states systems parameters could describe by quantum mechanical. In this article we study the dark exciton system (heavy hole and electron) in the spherical-symmetric potential (i.e. Coulomb), using quantum field theory and quantum mechanics technics. Today’s, calculation and analysis of the energy spectrum of the EXS in Coulomb potential with relativistic correction are very interesting subject in theoretical physics. This article contains a theoretical definition on the EXS characteristics that describes the Relativistic nature of interactions. Relativistic nature of interactions directly effect on the mass of particles and it is a good reason to study EXS system with exact data and describe how relativistic state could effect on the energy and mass spectrum in the EXS, and also how it is connected with excited states and how mass will be reduces in these states. The theoretically results for arising of the constituent mass of the EXS is calculated by taking into account relativistic corrections. The corrections on the energy and mass spectrum EXS with orbital excitations are calculated by taking into account relativistic corrections.
References
- ZH. Xuejun, et al.,‘Quantum Well Structures’, Phys. Rev. Lett. 74, 1995.
- A. A Slavnov, and L.D. Fadeev, "Introduction to Quantum Calibration Field", Nauka, Moscow, Russia, 1988.
- W. Greiner, Y. Reinhort, "Quantum Electrodynamics", 1st edition, Springer- Verleg, Germany. 1992.
- E.C. Aberc and B.V. Li, "Calibration Theory", Mir, Moscow, Russia, 1977.
- D. G.Duffy, "Green's Functions with Applications", Boca Raton, FL: Chapman & Hall/CRC, 2001.
- G. Arfken, "Nonhomogeneous Equation Green's Function, Mathematical Methods for Physicists", Orlando, FL: Academic, 1985.
- G. B. Arfken, and H. Weber, and F. E. Harris, "Mathematical Methods for Physicists",Orlando, FL: Academic Press, .2012).
- N.N. Bogolobov and D.B. Shirkov, "Introduction to Quantum Field Theory", Nauka, Moscow, Russia, 1984.
- C.C. Sheveber, "On the Relativistic Quantum Field Theory", Izdat. Ins. Literature, Moscow, Russia, 1963.
- R. Euost, "General Field Theory", Mir, Moscow, Russia,1967.
- D.J. Gross, and P. Wilezek, "Ultraviolet Behavior of Non-Abilene Gauge Theories", Phys. Rev. Lett., 30, 1343-1347, 1973.
- D.J. Gross and P. Wilezek, "Asymptotically Free Gauge Theories", Phys. Rev. DS, 3633-3639, 1973.
- M. Dineykhan, G. Efim,ov, "Oscillator Representatio in Quantum Physics", 1st edition, Springer- Verleg, Germany, 1995.
- M. Dineykhan, et al., "Mass spectrum bound state system with relativistic corrections", Journal of physics B: Atomic, Molecular and Optical Physics, 42(14), 145001, 2009.
- A. Jahanshir, "HydrogenAtom Mass Spectrum in the Excited States", Scientific Journal of Pure and Applied Sciences, 2(1), pp. 16-22, 2013.
- A. Jahanshir, "Mesonic Hydrogen Mass Spectrum in the Oscillator Representation", Journal of theoretical and applied physics, 3(4), 10-13, 2010.
- M. Dineykhan, and A. Jahanshir, and et al. "Mass Spectrum Bound State System with Relativistic Corrections", Journal of physics B: Atomic, Molecular and Optical Physics, 42(1), 145001, 2009.
- A. Jahanshir, "Mass Spectrum of Exotic Kaonic Nuclei in Relativistic Hamiltonian", Proceeding of the 4th Particle & Field Physics National Conference, The physics Society of Iran, Tehran, Iran, 2014.
- A. Jahanshir, "Determination of Relativistic Hamiltonian Effects in Exotic Kaonic Nuclei", Iranian Physics Conference,Urumiya University, Iran, 312-318, 2011.



