On Non-Canonical Solving the Satisfiability Problem
Anatoly D. Plotnikov*
Department of Social Informatics and Safety of Information Systems, Dalh East-Ukrainian National University, Luhansk, Ukraine
Abstract
We study the non-canonical method for solving the Satisfiability problem which given by a formula in the form of the conjunctive normal form. The essence of this method consists in counting the number of tuples of Boolean variables, on which at least one clause of the given formula is false. On this basis the solution of the problem obtains in the form YES or NO without constructing tuple, when the answer is YES. It is found that if the clause in the given formula has pairwise contrary literals, then the problem can be solved efficiently. However, when in the formula there are a long chain of clauses with pairwise a non-contrary literal, the solution leads to an exponential calculations.
Keywords
Satisfiability Problem, Satisfying Tuple, Disjunction, Clause, Conjunction, NP-Complete
Received: June 19, 2015
Accepted: July 22, 2015
Published online: August 4, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
To uniquely understand used terminology in the article, we recall some definitions.
Suppose we have a two-element set ![]() . The function f:
. The function f: ![]() is called Boolean. Every vector in
is called Boolean. Every vector in ![]() is considered as the tuple of values of variables
is considered as the tuple of values of variables ![]() of the function
of the function![]() .
.
A Boolean variable with negation or without negation is called literal. Literals x and ![]() is called contrary. The conjunction of r (1 £ r £ n) different non-contrary literals, called elementary. Any Boolean function can be represented as a disjunction of some elementary conjunctions. Such a representation of the function is called disjunctive normal form (DNF) of the function
is called contrary. The conjunction of r (1 £ r £ n) different non-contrary literals, called elementary. Any Boolean function can be represented as a disjunction of some elementary conjunctions. Such a representation of the function is called disjunctive normal form (DNF) of the function ![]() . For example, the function can be written as the following DNF:
. For example, the function can be written as the following DNF:
![]() .
.
A disjunction of different non-contrary literals called clause. Any Boolean function can be represented as a conjunction of some clauses. For example, the function given above in the form of the DNF can be written as CNF:
![]()
In the theory of computational complexity, the problems, belonging to the class NP, are considered. The problem Z belongs to the class NP if its solution can be verified by the time, described as a polinomial function on the dimension of the problem. Usually, a problem of the class NP formulated as a decision problem, that is, in the form of a question to which the answer (solution) is YES or NO. Thus, the solution of the problem — it is the answer YES or NO [2]. To verify the correctness of the answer to this question, some certificate should be submitted that in polynomial time on the dimension of the problem verifies the correctness of the answer.
However, in practice, the solution of the problem in form of a set of some parameters of the problem (vertices, edges, literals) is used as a certificate, allowing form the answer YES or NO. To obtain the certificate in such form is often difficult [11].
Of particular importance in the theory of computational complexity plays the satisfiability problem (SAT), which is formulated as follows [1,2]. Let it is given m clauses ![]() , containing variables
, containing variables ![]() . Has the formula
. Has the formula ![]() satisfiable assignment?
satisfiable assignment?
The SAT problem is one of NP-complete problems [1-10]. Historically, this is the first NP-complete problem. Solution of this problem is important for theory and practice.
Currently, to solve the SAT problem, DPLL algorithms found the greatest application which are based on the works of Davis and Putnam [12] and Davis Lodzhmana and Loveland [13]. The essence of these algorithms is to find a satisfying assignment for the SAT problem. The complexity of these algorithms can be described by an exponential formula of the dimension of the problem, since it is related to the construction of the tree of values of the variables of the problem [14].
The solution of the Satisfiability problem is called non-canonical if the answer YES or NO was obtained without presentation of variable values when a given formula is true.
The purpose of this article is to investigate of non-canonical method for solving the Satisfiability problem.
2. Basis of the Method
Let the formula of the Satisfiability problem is:
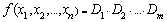 . (1)
. (1)
It is necessary to determine the existence of unknown values ![]() such that satisfy the function (1).
such that satisfy the function (1).
The formula (1) can be transformed by the operation of negation on it. As a result, we will obtain a new formula:
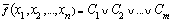 , (2)
, (2)
where each elementary conjunction obtained by the negation of the corresponding clause: ![]() =
=![]() (i =1, 2,..., m) in the formula (1).
(i =1, 2,..., m) in the formula (1).
Lemma 1. Each conjunction in the formula (2) determines a set of tuples of values of the variables of formula (1), for which the corresponding clause to be false.
Proof. In fact, in the formula (1), any clause is false if and only if every literal of this clause is false. Therefore, an elementary conjunction of the formula (2) must be true for the tuples on which the corresponding clause is false. What we wanted to prove. à
For example, suppose we have the formula:
![]() (3)
(3)
where ![]() ,
, ![]() ,
, ![]() .
.
The truth table for the clauses of this formula has the form:
Table 1. Table for the clauses.
| x1 | x2 | x3 | D1 | D2 | D3 |
| 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Executing a negation operation on the formula (3), we obtain the formula:
![]() (4)
(4)
Thus, we conclude that the set of elementary conjunctions of the formula (2) represents the set of all tuples of variables ![]() , on which at least one clause of formula (1) is false.
, on which at least one clause of formula (1) is false.
Theorem 1. The Satisfiable problem, determined on a set of variables, has a satisfiable assignment if and only if the total number of different tuples, on which at least one clause in the formula (1) is false, strictly smaller than ![]() .
.
Proof. This is evident. If the total number of tuples, in which at least one clause of formulas (1) is false, is equal to ![]() , then the satisfiable assignment does not exist for the Satisfiability problem. à
, then the satisfiable assignment does not exist for the Satisfiability problem. à
3. Certificate
Thus, according to Theorem 1 if we calculate the total number of different tuples, in which at least one clause in the Satisfiability problem is false, then on this basis, we can formulate the answer YES or NO to the question about existence of the satisfying assignment, that is, one can solve the Satisfiability problem, without constructing satisfying assignment. In this case, the certificate counts the total number of different tuples, in which at least one clause of the formula (1) is false.
Consider the different cases of the counting of tuples, in which clause of the formula (1) is false.
Lemma 2. Each conjunction ![]()
![]() of the equation (2), containing
of the equation (2), containing ![]() (1£
(1£ ![]() £ n) literals, determines
£ n) literals, determines ![]() tuples on which the corresponding clause of the formula (1) is false.
tuples on which the corresponding clause of the formula (1) is false.
Proof. Let us consider the elementary conjunction in the formula (2). Let ![]()
![]() is one of them. If the number of literals that make up the
is one of them. If the number of literals that make up the ![]() is
is ![]() (1 £
(1 £ ![]() £ n), then this conjunction defines
£ n), then this conjunction defines ![]() of tuples on which the corresponding clause of the formula (1) is false, because the (n -
of tuples on which the corresponding clause of the formula (1) is false, because the (n - ![]() ) missing literals can take all possible values. à
) missing literals can take all possible values. à
So, in the example (see Table 1 above), conjunction ![]() determines
determines ![]() tuples on which clause
tuples on which clause ![]() is false. Here we have n = 3;
is false. Here we have n = 3; ![]() = 2. These are tuples (010) and (011).
= 2. These are tuples (010) and (011).
Lemma 3. Any pair of clauses ![]() and
and ![]()
![]() of formula (2), containing contrary literals together, determines
of formula (2), containing contrary literals together, determines ![]() of tuples on which the corresponding clause of the formula (1) is false.
of tuples on which the corresponding clause of the formula (1) is false.
Proof. Let us now consider two clauses of the formula (2). Let it be the conjunctions of the ![]() and
and ![]()
![]() . Obviously, if the literal of the
. Obviously, if the literal of the ![]() has the contrary literal in
has the contrary literal in ![]() , then these conjunctions determine different tuples of variables. à
, then these conjunctions determine different tuples of variables. à
For example, two elementary conjunctions in the formula (4) ![]() and
and ![]()
![]() contain the variable
contain the variable ![]() with negation and without negation. The conjunction
with negation and without negation. The conjunction ![]() determines tuples (100) and (110), which does not coincide with the tuples, represented by the conjunction
determines tuples (100) and (110), which does not coincide with the tuples, represented by the conjunction ![]() ((010), (011)).
((010), (011)).
The considered conjunctions are called alternative.
Theorem 2. Let the formula (2) contains only pairwise alternative conjunctions ![]()
![]() . Then the total number of tuples, on which the corresponding clause of the formula (1) is false, is equal
. Then the total number of tuples, on which the corresponding clause of the formula (1) is false, is equal
![]() .
.
Proof. It follows from Lemma 3. à
It is easy to see that the formula (4) contains pairwise alternative conjunctions. The total number of tuples, on which the corresponding clauses in the formulas (3) is false, is equal:
21 + 21 + 21 = 6,
that is, the formula (3) has ![]() satisfiable tuples. In this case, the solution of the problem is YES.
satisfiable tuples. In this case, the solution of the problem is YES.
Theorem 3. Any Boolean function, represented by the formula (2), can be transformed into a formula containing only pairwise alternative conjunctions.
Proof. Any Boolean function can be represented as a perfect disjunctive normal form (PDNF), which contains only pairwise alternative conjunctions, each of which depends on n variables. For example, a pair of conjunctions ![]() can be transformed as follows:
can be transformed as follows:
![]()
![]() à
à
Unfortunately the time (the number of operations), that is required to build PDNF, can be unacceptably large.
Let there is some conjunction ![]() containing
containing ![]() literals from n (
literals from n (![]() £ n). The variables, which do not have their own literals in
£ n). The variables, which do not have their own literals in ![]() , called free for the given conjunction. The number of such free variables in the conjunction
, called free for the given conjunction. The number of such free variables in the conjunction ![]() equal to
equal to ![]() . Similarly, if there are p conjunctions
. Similarly, if there are p conjunctions![]() , then the total number of free variables in these conjunctions is designated as
, then the total number of free variables in these conjunctions is designated as ![]() .
.
Theorem 4. Let the formula (2) has p conjunctions ![]() , having no pairwise alternative literals. Then the total number of tuples, on which this conjunction is false, is equal to:
, having no pairwise alternative literals. Then the total number of tuples, on which this conjunction is false, is equal to:
![]() (5)
(5)
Proof. The validity of Theorem 4 follows from the method of inclusions and exclusions. à
Consider a chain of pairwise non-alternative conjunctions ![]() ,
,![]() ,
, ![]() . The total number of tuples, on which the corresponding disjunctions are false, is equal to:
. The total number of tuples, on which the corresponding disjunctions are false, is equal to:
R = 23 + 23 + 22 - 22 - 21 - 21 + 20 = 13.
Theorem 5. Let the formula (2) has p conjunctions ![]() , having no pairwise alternative literals. Then the number of members in the formula (5) is equal to
, having no pairwise alternative literals. Then the number of members in the formula (5) is equal to ![]() .
.
Proof. The number of members in the formula (5) equals the number of subsets of a fnite p-set without empty subset.à
4. Conclusions
Consideration of non-canonical method for solving the Satisfiability problem shows that this method can be used effectively for solving problems, initially containing pairwise of alternative conjunctions. Unfortunately, in the general case, solving the problem by the considered method is ineffectively as it involves performing an exponential number of operations. Therefore, this method can be used with a limited number of chains of pairwise non-alternative conjunctions. Obviously, this depends on the performance of the used computer.
References
- Garey M.R. and Johnson D.S. (1979) Computers and Intractability. W.H. Freeman and Company, San Francisco.
- Papadimitriou C.H. and Steiglitz K. (1982) Combinatorial optimization: Algorithms and complexity. Prentice-Hall Inc., New Jersey.
- Cook S. (1971) The Complexity of Theorem-Proving Procedures. Proceedings of the 3rd Annual ACM Symposium on Theory of Computing: pp. 151–158.
- Karp R.M. (1972) Reducibility among combinatorial problems. In Miller, Raymond E.: Thatcher,James W. Complexity of Computer Computations. Plenum. pp. 85–103.
- Crescenzi P. and Kann V. (1997) Approximation on the Web: A Compendium of NP Optimization Problems. Proceedings of International Workshop RANDOM’97, Bologna, 11-12 July 1997, pp. 111-118.
- Dunne P.E. (2008) An annotated list of selected NP-complete problems. COMP202, Dept. of Computer Science, University of Liverpool.
- Levin L.A. (1973) Universal Searching Problems. Prob. Info. Transm. 9, 265-266.
- Valiant L. (1979) The complexity of computing the permanent. Theoret. Comput. Sci., 8, pp. 189–201.
- Papadimitriou C.H. (1994) Computational Complexity (1st ed.). Addison Wesley. Chapter 9 (NP–complete problems). pp. 181–218.
- Jiang J.R. (2008), The theory of NP-completeness. Dept. of Computer Science and Information Engineering. National Central University, Jhongli City, Taiwan.
- Plotnikov A.D. (2012)Heuristic algorithm for finding the maximum independent set.Cybernetics and Systems Analysis: Volume 48, Issue 5, Page 673-680.
- Davis M., Putman H. 1960) A computing procedure for quantification theory // Journal of the ACM. 7 (3). p. 201–215.
- Davis M., Logeman G., Loveland D. (1962) A machine program for theorem-proving // Communications of the ACM. 5 (7). p. 394–397.
- Kullmann O. (1999) New methods for 3-SAT decision and worst-case analysis // Theoretical Computer Science. 223 (1–2). p. 1–72.



