A Diverse Clustering Method on Biological Big Data
Mohsen Rezaei*
Department of Computer Engineering, Nourabad Mamasani Branch, Islamic Azad University, Nourabad, Iran
Abstract
In the past decade many new methods were proposed for creating diverse classifiers due to combination. In this paper a new method for constructing an ensemble is proposed which uses clustering technique to generate perturbation in training datasets. Main presumption of this method is that the clustering algorithm used can find the natural groups of data in feature space. During testing, the classifiers whose votes are considered as being reliable are combined using majority voting. This method of combination outperforms the ensemble of all classifiers considerably on several real and artificial datasets.
Keywords
Diversity, Classifier Fusion, Clustering, Classifier Ensembles
Received: June 16, 2015
Accepted: June 28, 2015
Published online: July 27, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
Nowadays, usage of recognition systems has addressed many applications in almost all fields. However, Most of classification algorithms have obtained good performance for specific problems; they lack enough robustness for other problems. Therefore, recent researches are directed to the combinational methods which have more power, robustness, resistance, accuracy and generality[1] and [2].
Combinational methods usually result in the improvement of classification, because classifiers with different features and methodologies can complete each other [4]-[6]. Kuncheva in [7,35,36,37,38] using Condorcet Jury theorem [8], has shown that combination of classifiers can usually operate better than single classifier. of combinational classifier systems are represented in [9]-[11]-[39-44]. Valentini and Masouli divide methods of combining classifiers into two categories: generative methods, nongenerative methods. In generative methods, a set of base classifiers is created by a set of base algorithms or by manipulating dataset. This is done in order to reinforce diversity of base classifiers [9], [10]. For a good coverage on combinational methods the reader is referred to [1], [7], and [12]-[16].
In other words, the individual classifiers make their errors on difference parts of the input space [16] and [17]. Many approaches have been proposed to construct such ensembles. One group of these methods obtains diverse individuals by training accurate classifiers on different training set, such as bagging, boosting, cross validation and using artificial training examples [17]-[20]-[45-47]. Another group of these methods adopts different topologies, initial weight setting, parameter setting and training algorithm to obtain individuals. For example, Rosen in [21] adjusted the training algorithm of the network by introducing a penalty term to encourage individual networks to be decorrelated. Liu and Yao in [22] used negative correlation learning to generate negatively correlated individual neural network. The third group is named selective approach group where the diverse components are selected from a number of trained accurate networks. For example, Opitz and Shavlik in [23] proposed a generic algorithm to search for a highly diverse set of accurate networks. Lazarevic and Obradoric in [24] proposed a pruning algorithm to eliminate redundant classifiers; Navone et al. in [25] proposed another selective algorithm based on bias/variance decomposition; GASEN proposed by Zhou et al. in [26] and PSO based approach proposed by Fu et al. in [27] also were introduced to select the ensemble components.
The representative of the first category is AdaBoost [28], which sequentially generates a series of base classifiers where the training instances wrongly predicted by a base classifier will play more important role in the training of its subsequent classifier. The representative of the second category is Bagging [18], which generates many samples from the original training set via bootstrap sampling [29] and then trains a base classifier from each of these samples, whose predictions are combined via majority voting.
The new classification systems try to investigate errors and propose a solution to compensate them [30]. One of these approaches is combination of classifiers. Dietterich in [31] has proved that a combination of classifiers is usually better than a single classifier, by three kinds of reasoning: Statistical, computational and pictorial reasoning. However, there are many ways to combine classifiers; there is no proof to determine the best one [32].
2. Combining Classifiers
In general, creation of combinational classifiers may be in four levels. It means combining of classifiers may happen in four levels. Figure 1 depicts these four levels. In level four, we try to create different subset of data in order to make independent classifiers. Bagging and boosting are examples of this method [18], [33]. In these examples, we use different subset of data instead of all data for training. In level three, we use subset of features for obtaining diversity in ensemble. In this method, each classifier is trained on different subset of features [32], [34]-[35]. In level two, we can use different kind of classifiers for creating the ensemble [32]. Finally, in the level one, method of combining (fusion) is considered.
In the combining of classifiers, we aim to increase the performance of classification. There are several ways for combining classifiers. The simplest way is to find best classifier and use it as main classifier. This method is offline CMC. Another method that is named online CMC uses all classifier in ensemble, for example, by voting. We will show that combining method can improve the result of classification.
3. Proposed Method
For example in Farsi handwritten optical character recognition problem, digit 5 is written at least in two kinds of shape (2 clusters).
In [36], it is shown that changing labels of classes can improve classification performance. So initial digit ‘5’ class is divided into two subclasses, digit ‘5’ type 1 and digit ‘5’ type 2, in order to ease classification goal of learning digit ‘5’ initial class complicated boundaries.
According to [7], if we have some really independent classifiers better than random classifiers, the simple ensemble (majority vote) of them can outperform their average performance in accuracy. Generally even if we increase the number of those independent classifiers, we can reach to any arbitrary accuracy, even 100%. But the problem restricting us for this goal is our incapability in obtaining those really independent classifiers.

Figure 1. Data of class ‘5’ and ‘0’; 5 is in left and 0 is in right.
In proposed solution, according to error rate of each class, the class is divided into some subclasses in order to ease learning of decision boundaries by classifier. For a better understanding have a look at Figure 2.
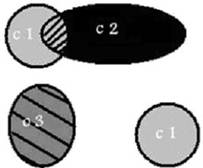
Figure 2. A dataset with 3 class in which class 1 contain 2 subclass.
As we can see, number of classes has changed in Figure 2. This problem in dimension more than 2 will be probably more crucial. In this article the presumption is that a class is composed of more than one cluster which means that in a classification process with c classes, the number of real classes may be different from c.
Pseudo code of proposed algorithm:
Algorithm1(original data set);
m(1: number_of_classes)=1;
validation data, training data, test data = extract (original data set);
end for
ensemble=majority_vote(out(1.. max_iteration));
accuracy=compute_accuracy(ensemble);
return accuracy,save_classifiers;
As you can see at the bellow, this method get dataset as input, and put it into three partitions: training set, test set and validation set. Here, the training set, test set and validation set contain 60%, 15% and 25% of entire dataset respectively. Then the data of each class is extracted from the original training dataset. Firstly we initial the number of cluster in each class to one. After that we repeat the following process as many as the predetermined number. This predetermined number is considered 10 here:
For simplicity assume that time order of clustering and training a classifier on a dataset are approximately the same. Of course this waste of time is completely tolerable against important achieved accuracy.
This approach is tested on real datasets WDBC, BUPA and BALANCE SCALE and also non-real datasets number 1, 2 and 3. You can see these three datasets in Figure 3.

Figure 3. 3 dataset number 1, 2 and 3 left to right respectively.
All these non-real datasets contain 300 data points and 3 classes. Also they are 2-dimentional. The results are reported in tables 1-2.
As it is inferred from tables 1 to 2, different iterations has resulted in diverse and usually better accuracy than initial classifier. This method is evaluated on iris dataset and result shows such a little improvement that we prefer not to report it. It can be result of special shapes of iris classes as each of them is composed of only one dense cluster and not more.
4. Conclusion
As it was mentioned before, this method is sensitive to shape of dataset. It cannot work well on those of datasets with very singular dense classes.
Table 1. Result of proposed algorithm’s run on unreal dataset number 1.
| Itearation 1 | Itearation 2 | Itearation 3 | Itearation 4 | Itearation 5 | Ensemble | Average | |
| Run 1 | 0.75 | 0.73333 | 0.76667 | 0.75 | 0.78333 | 0.8 | 0.7567 |
| Run 2 | 0.75 | 0.76667 | 0.6 | 0.66667 | 0.78333 | 0.7667 | 0.7133 |
Table 2. Result of proposed algorithm’s run on unreal dataset number 2.
| Itearation 1 | Itearation 2 | Itearation 3 | Itearation 4 | Itearation 5 | Ensemble | Average | |
| Run 1 | 0.75 | 0.76667 | 0.73333 | 0.71667 | 0.76667 | 0.76667 | 0.7467 |
| Run 2 | 0.68333 | 0.7 | 0.68333 | 0.73333 | 0.66667 | 0.7167 | 0.6933 |
References
- B. Minaei-Bidgoli, G. Kortemeyer and W.F. Punch, Optimizing Classification Ensembles via a Genetic Algorithm for a Web-based Educational System, (SSPR /SPR 2004), Lecture Notes in Computer Science (LNCS), Volume 3138, Springer-Verlag, ISBN: 3-540-22570-6, pp. 397-406, 2004.
- Saberi., M. Vahidi, B. Minaei-Bidgoli, Learn to Detect Phishing Scams Using Learning and Ensemble Methods, IEEE/WIC/ACM International Conference on Intelligent Agent Technology, Workshops (IAT 07), pp. 311-314, Silicon Valley, USA, November 2-5, 2007.
- T.G. Dietterich, Ensemble learning, in The Handbook of Brain Theory and Neural Networks, 2nd edition, M.A. Arbib, Ed. Cambridge, MA: MIT Press, 2002.
- H. Parvin, H. Alinejad-Rokny, S. Parvin, Divide and Conquer Classification, Australian Journal of Basic & Applied Sciences, 5(12), 2446-2452 (2011).
- H. Parvin, B. Minaei-Bidgoli, H. Alinejad-Rokny, A New Imbalanced Learning and Dictions Tree Method for Breast Cancer Diagnosis, Journal of Bionanoscience, 7(6), 673-678 (2013).
- H. Parvin, H. Alinejad-Rokny, M. Asadi, An Ensemble Based Approach for Feature Selection, Journal of Applied Sciences Research, 7(9), 33-43 (2011).
- S. Gunter and H. Bunke, Creation of classifier ensembles for handwritten word recognition using feature selection algorithms, IWFHR 2002 on January 15, 2002.
- B. Minaei-Bidgoli, G. Kortemeyer, W. F. Punch, Mining Feature Importance: Applying Evolutionary Algorithms within a Web-Based Educational System, Proc. of the Int. Conf. on Cybernetics and Information Technologies, Systems and Applications, CITSA 2004.
- L. I. Kuncheva, Combining Pattern Classifiers, Methods and Algorithms, New York: Wiley, 2005.
- L. Shapley and B. Grofman, Optimizing group judgmental accuracy in the presence of interdependencies, Public Choice, 43:329-343, 1984.
- H. Parvin, H. Helmi, B. Minaie-Bidgoli, H. Alinejad-Rokny, H. Shirgahi, Linkage learning based on differences in local optimums of building blocks with one optima, International Journal of Physical Sciences, 6(14), 3419-3425 (2011).
- H. Parvin, B. Minaei-Bidgoli, H. Alinejad-Rokny, S. Ghatei, An innovative combination of particle swarm optimization, learning automaton and great deluge algorithms for dynamic environments, International Journal of Physical Sciences, 6(22), 5121-5127 (2011).
- H. Parvin, H. Alinejad-Rokny, S. Parvin, A Classifier Ensemble of Binary Classifier Ensembles, International Journal of Learning Management Systems, 1(2), 37-47 (2013).
- F. Roli and J. Kittler, editors. Proc. 2nd Int. Workshop on Multiple Classifier Systems (MCS 2001), Vol. 2096 of Lecture Notes in Computer Science LNCS Springer-Verlag, Cambridge, UK, 2001.
- F. Roli and J. Kittler, editors. Proc. 3rd Int. Workshop on Multiple Classifier Systems (MCS 2002), Vol. 2364 of Lecture Notes in Computer Science LNCS Springer-Verlag, Cagliari, Italy, 2002.
- L. Lam. Classifier combinations: implementations and theoretical issues. In J. Kittler and F. Roli, editors, Multiple Classifier Systems, Vol. 1857 of Lecture Notes in Computer Science, Cagliari, Italy, 2000, Springer, pp. 78-86.
- T.G. Dietrich, Machine-learning research: four current direction, AI Magazine, 18, 4, winter 1997, 97-135.
- H. Parvin, B. Minaei-Bidgoli, H. Alinejad-Rokny, W.F. Punch, Data weighing mechanisms for clustering ensembles, Computers & Electrical Engineering, 39(5), 1433-1450 (2013).
- H. Parvin, H. Alinejad-Rokny, B. Minaei-Bidgoli, S. Parvin, A new classifier ensemble methodology based on subspace learning, Journal of Experimental & Theoretical Artificial Intelligence, 25(2), 227-250 (2013).
- H. Parvin, H. Alinejad-Rokny, N. Seyedaghaee, S. Parvin, A Heuristic Scalable Classifier Ensemble of Binary Classifier Ensembles, Journal of Bioinformatics and Intelligent Control, 1(2), 163-170 (2013).
- A.K. Jain, R.P.W. Duin, J. Mao, Satanical pattern recognition: a review, IEEE Transaction on Pattern Analysis and Machine Intelligence, PAMI-22, 1, January 2000, 4-37.
- R. O. Duda, P. E. Hart, and D. G. Stork, Pattern Classification, 2nd ed. John Wiley & Sons, NY, 2001.
- J. C. Sharkey, editor, Combining Artificial Neural Nets. Ensemble and Modular Multi-Net Systems, Springer-Verlag, London, 1999.
- L. K. Hansen, P. Salamon, Neural network ensembles. IEEE Transaction on Pattern Analysis and Machine Intelligence, 12(10):993-1001, 1990.
- Krogh, J. Vedelsdy, Neural Network Ensembles Cross Validation, and Active Learning, In: G. Tesauro, D. Touretzky, T. Leen (Eds.), Advances in Neural Information Processing Systems, Volume 7. MIT Press, Cambridge, MA, p.231-238, 1995.
- L. Breiman, Bagging predictors. Machine Learning, 24(2):123-140, 1996.
- R.E. Schapire, The strength of weak learn ability, Machine Learning, 5(2):1971-227, 1990.
- P. Melville, R. Mooney, Constructing Diverse Classifier Ensembles Using Artificial Training Examples, Proc. of the IJCAI-2003, Acapulco, Mexico, p.505-510, 2003.
- B. E. Rosen, Ensemble learning using decorrelated neural network. Connection Science, 8(3-4):373-384, 1996.
- Y. Liu, X. Yao, Evolutionary ensembles with negative correlation learning, IEEE Trans. Evolutionary Computation, 4(4):380-387, 2000.
- D. Opitz, J. Shavlik, Actively searching for an effective neural network ensemble, Connection Science, 8(3-4):337-353, 1996.
- Parvin, H. Alinejad-Rokny, N. Seyedaghaee, S. Parvin, A Heuristic Scalable Classifier Ensemble of Binary Classifier Ensembles, Journal of Bioinformatics and Intelligent Control, 1(2), 163-170 (2013).
- Lazarevic, Z. Obradovic, Effective pruning of neural network classifier ensembles. Proc. International Joint Conference on Neural Networks, 2:796-801, 2001.
- H. D. Navone, P. F. Verdes, P. M. Granitto, H. A. Ceccatto, Selecting Diverse Members of Neural Network Ensembles, Proc. 16th Brazilian Symposium on Neural Networks, p.255-260, 2000.
- Z. H. Zhou, J. X. Wu, Y. Jiang, S. F. Chen, Genetic algorithm based selective neural network ensemble, Proc. 17th International Joint Conference on Artificial Intelligence, 2:797-802, 2001.
- M.H. Fouladgar, B. Minaei-Bidgoli, H. Parvin, H. Alinejad-Rokny, Extension in The Case of Arrays in Daikon like Tools, Advanced Engineering Technology and Application, 2(1), 5-10 (2013).
- H. Parvin, M. MirnabiBaboli, H. Alinejad-Rokny, Proposing a Classifier Ensemble Framework Based on Classifier Selection and Decision Tree, Engineering Applications of Artificial Intelligence, 37, 34-42 (2015).
- H. Parvin, B. Minaei-Bidgoli, H. Alinejad-Rokny, W.F. Punch, Data weighing mechanisms for clustering ensembles, Computers & Electrical Engineering, 39(5), 1433-1450 (2013).
- Q. Fu, S. X. Hu, S. Y. Zhao, A PSO-based approach for neural network ensemble, Journal of Zhejiang University (Engineering Science), 38(12):1596-1600, 2004, (in Chinese).
- Y. Freund, R.E. Schapire, A decision-theoretic generalization of online learning and an application to boosting, in Proceedings of the 2nd European Conference on Computational Learning Theory, Barcelona, Spain, pp.23–37, 1995.
- B. Efron, R. Tibshirani, An Introduction to the Bootstrap, New York: Chapman & Hall, 1993.
- V. Dobra, Scalable Classification And Regression Tree Construction, Ph.D. Dissertation, Cornell University, Ithaca, NY, 2003.
- T. G. Dietterich, Ensemble methods in machine learning. In J. Kittler and F. Roli, editors, Multiple Classifier Systems, volume 1857 of Lecture Notes in Computer Science, Springer, pp. 1–15, Cagliari, Italy, 2000.
- F. Roli, G. Giacinto, G. Vernazza.Methods for designing multiple classifier systems. In J. Kittler and F. Roli, editors, Proc. 2nd International Workshop on Multiple Classifier Systems, Vol. 2096 of Lecture Notes in Computer Science, Springer- Verlag, pp. 78–87, Cambridge, UK, 2001.
- S. Dudoit, J. Fridlyand, Bagging to improve the accuracy of a clustering procedure. Bioinformatics, 19 (9), pp. 1090-1099, 2003.
- L.I. Kuncheva, L.C. Jain, Designing Classifier Fusion Systems by Genetic Algorithms. IEEE Transaction on Evolutionary Computation, Vol. 33, 351-373, 2000.
- Strehl, J. Ghosh, Cluster ensembles a knowledge reuse framework for combining multiple partitions. Journal on Machine Learning Research, pp. 583-617, 2002.



