MIMO Channel Correlation and System Capacity Analysis
Isiaka A. Alimi*, Kayode F. Akingbade, Jide J. Popoola, Michael O. Kolawole
Department of Electrical and Electronics Engineering, School of Engineering and Engineering Technology, Federal University of Technology, Akure, Nigeria
Abstract
Over the last two decades, wireless communication services and applications worldwide have witnessed exponential growth with corresponding progression in subscribers’ population but without resultant increase in bandwidth required for their effective functionality. Solution to this challenge has led to the adoption of multiple-input–multiple-output (MIMO) systems prevalent in the emerging wireless communication technologies because of their high capacity. This paper investigates the capacity distribution of MIMO systems with arbitrary correlation among the antennas in frequency-flat Rayleigh environments. In addition, the capacity of spatially correlated MIMO channels is evaluated with and without channel state information (CSI) at the transmitter. Through simulation, this study observed that channel capacity increases as signal correlation decreases, while bit error rate increases with increase in signal correlation. Consequently, as the channel becomes progressively correlated in space, the probability of multiplexing gain for the MIMO communication system reduces considerably.
Keywords
Channel State Information (CSI), Singular Value Decomposition (SVD), Rayleigh-Fading Channels, Correlation, Diversity, MIMO
Received: April 6, 2015 / Accepted: April 20, 2015 / Published online: May 11, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
The emerging wireless communication systems require sufficient bandwidth to support the increasing subscribers’ data rate demand that grows exponentially on daily basis [1,2]. The multiple-input–multiple output (MIMO) systems have become an attractive potential solution to bridging the gap between the higher data rates required by the subscribers and the bandwidth, which is a scarce resource in wireless communication systems [3]. Additionally, MIMO scheme has advanced and is being supported as a result of its advantages by various wireless communication standards such as worldwide interoperability for microwave access (WiMAX), long term evolution (LTE) and wireless local area networks (WLANs) in achieving spatial diversity to combat fading. MIMO scheme offers significant increase in link capacity, link range, reliability and spectral efficiency without additional bandwidth or increased transmit power for the wireless systems [1,4]. It was shown in [5] that the use of multiple transmit and receive antennas can provide significantly high spectral efficiency for wireless communication systems in the multipath fading environments. Theoretically the capacities of MIMO systems increase linearly with the number of transmit and receive antenna elements when the channel gains are uncorrelated [6] as a consequence of their channels’ decomposition into an equivalent set of parallel spatial sub-channels. On the downside, signal correlation limits the achievable capacity of MIMO systems thereby diminishing the achievable benefit of the use of diversity technique[7,8]. The signal correlation exists in realistic environments due to insufficient antenna spacing and sparse scattering environments. The common channel model that has been employed in MIMO performance-analysis is the Kronecker model in which the correlation properties of the MIMO channel are modeled at both the transmitter and receiver separately. The model neglects the statistical interdependency between scattering distributions at the transmitter and receiver antenna apertures[8].The achievable rate of the MIMO systems depends considerably on the amount of channel state information (CSI) available at the receivers and the transmitters[9]. Realistically, the CSI is perceived perfect only at the receiver and perceived feedback to, and partially available at, the transmitter with zero delay estimation; thus allowing, via water-filling scheme, optimal distribution of total available power among the transmit antennas [10,11]. In effect, the availability of partial CSI at the transmitter can enhance MIMO system performance by substantively increasing the spectral efficiency or reducing the error probability. In [12], study on the characteristics of signal fluctuation and effects of multipath on MIMO channel correlation of satellite-to-ground communications in the rainfall scattering environment. Also, [13] investigates the different roles of time-of-arrival and amplitude correlations in characterizing space–frequency -correlated ultrawideband MIMO channels. This study aims at investigating MIMO systems performance metrics in terms of error probability and the information theoretic capacity of the systems.
The rest of this paper is arranged as follows: Section 2 presents a brief review on correlated MIMO channel system model. In Section 3, the activities involved in carrying out this study are presented, as well as the correlated and uncorrelated MIMO channel capacities. Section 4 presents the performance curves’ results generated based on models simulation developed in MATLAB® while Section 5 concludes this paper.
2. Correlated MIMO Channel System Model
This MIMO model employs receive and transmit correlation matrices. The wireless MIMO channel consists of non-line-of-sight (NLOS) Rayleigh matrix HNLOS, and the fixed line-of-sight (LOS) matrix HLOS. Considering target group n channel models, the MIMO channel matrix H in their delay profile is the sum of fixed LOS and NLOS matrices given as [3,8,9,14]:
![]() (1)
(1)
where P is the power delay profile, which is the sum of the fixed LOS power (PLOS) and the variable NLOS power (PNLOS) of the channel; and K is the Ricean factor which is the relative strength of the LOS component relative to NLOS, i.e.
![]() (2)
(2)
Nominally, the value of K in Eqn. (1) determines the distribution pattern of the channel. For instance, when K = 0, the LOS matrix term is cancelled and the channel’s distribution is Rayleigh. On the other hand, when K ≠ 0, the channel in Eqn. (1) may or may not contain NLOS components. With increasing values of K, the channel becomes progressively correlated in space, thus reducing the probability of multiplexing gain for the MIMO communication system. The development of ergodic capacity requires the assumption that channels created by MIMO are independent. In a real scenario, there are elements of correlation among the channels that appear to degrade the ergodic capacity. The signal correlations are caused by lack of multipath components and this is the reason why rich multipath components are required in MIMO systems [1]. Whilst the presence of rich multipath components may be responsible for signal décor relation, it also leads to different spatial signatures of the received signals. With the knowledge of channel statistics, the receiver is able to differentiate and recover data symbols through the exploitation of the difference in spatial signatures. Of course, the correlation of MIMO channels can be as a result of separation and arrangement of antennas at both side of the link. The correlation caused by antenna separation can be prevented by spacing the antennas by at least![]() , (where
, (where ![]() is the wavelength of the carrier frequency).If the rich multipath results in antenna décor relation and full channel rank, then the MIMO links would offer capacity gains that are proportional to the minimum of the number of transmit and receive antennas. Consequently, we can write the channel matrix with spatial correlation as [15-17]:
is the wavelength of the carrier frequency).If the rich multipath results in antenna décor relation and full channel rank, then the MIMO links would offer capacity gains that are proportional to the minimum of the number of transmit and receive antennas. Consequently, we can write the channel matrix with spatial correlation as [15-17]:
![]() (3)
(3)
where
(.) H is Hermitian transposition.
![]() is a matrix of independent zero mean, unit variance, complex Gaussian random variables that has been subjected to correlation effects.
is a matrix of independent zero mean, unit variance, complex Gaussian random variables that has been subjected to correlation effects.
![]() is the transmit correlation matrix; i.e., the correlation between the transmit antenna signals that is determined by the angle-of-departure from the transmitter and transmit side power angular spectrum (PAS).
is the transmit correlation matrix; i.e., the correlation between the transmit antenna signals that is determined by the angle-of-departure from the transmitter and transmit side power angular spectrum (PAS).
![]() is the receive correlation matrix; i.e., the correlation between receive antenna signals that is determined by the angle-of-arrival at the receiver and receive side PAS.
is the receive correlation matrix; i.e., the correlation between receive antenna signals that is determined by the angle-of-arrival at the receiver and receive side PAS.
The correlation across the transmit and receive antennas results in spatially dependent fading—also referred to as spatial selectivity—whose matrices expressed thus;
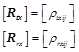 (4)
(4)
where ![]() and
and ![]() are, respectively, the complex correlation coefficients between i-th receive and j-th transmit antennas.
are, respectively, the complex correlation coefficients between i-th receive and j-th transmit antennas.
3. Developed Model for the MIMO Channel Capacity
The achievable capacity gain of MIMO wireless systems depends largely on correlation between the channel coefficients of radio channels. A correlated MIMO radio channel offers less capacity gain compare with uncorrelated radio channels. The potential capacity gain for each scenario is analysed.
3.1. Uncorrelated MIMO Channel Capacity
Assuming a generalized MIMO scheme with ![]() transmit antennas and
transmit antennas and ![]() receive antennas, the received signal vector model
receive antennas, the received signal vector model![]() , corresponding to the transmission through a flat-fading MIMO channel is expressed as [18];
, corresponding to the transmission through a flat-fading MIMO channel is expressed as [18];
![]() (5)
(5)
where ![]() is the transmitted signal vector,
is the transmitted signal vector, ![]() is the channel matrix between transmitter and receiver, also known as channel state information (CSI), which has zero-mean circularly symmetric complex Gaussian entries with unit variance and
is the channel matrix between transmitter and receiver, also known as channel state information (CSI), which has zero-mean circularly symmetric complex Gaussian entries with unit variance and ![]() is the complex additive white Gaussian noise vector with variance,
is the complex additive white Gaussian noise vector with variance, ![]() .
.
The MIMO channel capacity can be established using Singular Value Decomposition (SVD) which is a technique for solving sets of linear equations and matrices [9]. This numerical method is used in analysing the complex path between the transmitter and the receiver for simplification purposes. It is also useful in decomposing the MIMO channel matrix ![]() into a set of independent equivalent single-input single-output (SISO) channels.
into a set of independent equivalent single-input single-output (SISO) channels.
For a complex matrix![]() , the SVD is expressed as [16,18]:
, the SVD is expressed as [16,18]:
![]() (6)
(6)
where ![]() denotes the conjugate transpose,
denotes the conjugate transpose,![]() is a diagonal matrix with singular values equal to the square root of eigenvalues of the Wishart matrix, denoted as
is a diagonal matrix with singular values equal to the square root of eigenvalues of the Wishart matrix, denoted as![]() such that the condition
such that the condition![]() is satisfied. Also,
is satisfied. Also,![]() and the Wishart matrix W, is defined as [19]:
and the Wishart matrix W, is defined as [19]:
![]() (7)
(7)
Considering MIMO eigenmode system shown in Figure 1, the received signal at the input of the received filter is represented as:
![]() (8)
(8)
Substituting (6) in (8) gives;
![]() (9)
(9)
If there is full channel state information (CSI) at the transmitter, the transmit filter is denoted as ![]() and matched receive filter as
and matched receive filter as![]() . Hence, the estimated received signal
. Hence, the estimated received signal![]() , is represented as:
, is represented as:
![]() (10)
(10)
Substituting (9) in (10) gives:
![]() (11)
(11)
But the transmitted signal is given as:
![]() (12)
(12)
Hence, substituting (12) in (11) gives:
![]() (13)
(13)
or
![]() (14)
(14)
which in the component wise as
![]() (15)
(15)
Therefore, MIMO equivalent channel consists of ![]() parallel spatial sub-channels
parallel spatial sub-channels ![]() with different eigenvalues
with different eigenvalues![]() . The diagonal matrix
. The diagonal matrix ![]() signifies that the system is equivalent parallel SISO channels and determines the number of independent parallel channels available in the channel matrix
signifies that the system is equivalent parallel SISO channels and determines the number of independent parallel channels available in the channel matrix![]() ; given by the number of non-zero diagonal eigenvalues, of which each gives the rank of that particular subchannel.
; given by the number of non-zero diagonal eigenvalues, of which each gives the rank of that particular subchannel.
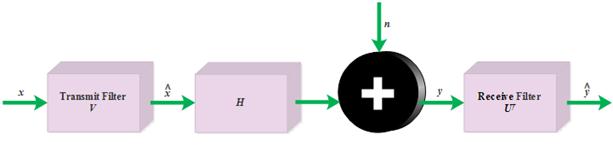
Figure 1. MIMO Eigenmode System Conditions over Flat-fading Rayleigh channel.
This implies that the probable capacity that a MIMO channel can support depends on the number of obtainable spatial eigenmodes of the channel matrix. The channel eigenmodes(or principle components) can be regarded as individual channels characterized by coefficients (eigenvalues). According to Shannon’s capacity formula, the capacity of MIMO channel can be derived given the transmit power pk. As noted in [2,8,20], the MIMO channel capacity can be expressed as
![]() bits/sec/Hz (16)
bits/sec/Hz (16)
![]() (17)
(17)
![]() (18)
(18)
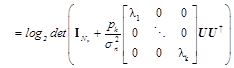 (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
When there is no CSI at the transmitter, the ideal approach will be to allocate the power equally among the transmit antenna elements![]() given the total transmit power pt. Therefore, the capacity without CSI is given as:
given the total transmit power pt. Therefore, the capacity without CSI is given as:
![]() (23)
(23)
3.2. Correlated MIMO Channel Capacity
The symmetric orthogonal channels are required in a MIMO system to prevent the loss of transmitted information. This is due to the fact that they do not have null modes—the state in which the eigenvalues equal to zero. Furthermore, symmetric orthogonal channels can be inverted at the receiver without noise amplification leading to an enhanced system performance. The spread of the eigenvalues is a measure of the orthogonality of the MIMO channel. A large eigenvalue spread implies that the channel matrix is highly non-orthogonal and vice-versa. Also, the orthogonality of a MIMO channel is measured by the condition number and effective degrees of freedom(EDOF) [1,8]. The condition number of a matrix is defined by the ratio of its largest and smallest nonzero eigenvalues; defined as [14]:
![]() (24)
(24)
Thus, a condition number of unity implies that the channel matrix is orthogonal. Conversely, a large condition number indicates that the channel is highly non-orthogonal or ill conditioned and this results in a poor channel capacity.
Moreover, the concept of EDOF is introduced to be able to analyse the corresponding value of the number of subchannels that actually contribute to the information transfer or, better still, that represent the number of subchannels that are actively participating in conveying information over a given wireless MIMO link. Mathematically, the EDOF value indicates the non-zero singular values of the channel matrix H and it is determined by the spatial correlation of H. The channel capacity with correlation can be expressed using (3) and (16) as:
![]() bits/sec/Hz (25)
bits/sec/Hz (25)
Using the equality![]() , then (25) becomes;
, then (25) becomes;
![]() (26)
(26)
when ![]() and signal-to-noise ratio(SNR) is high, expression for the capacity can be estimated as:
and signal-to-noise ratio(SNR) is high, expression for the capacity can be estimated as:
![]() (27)
(27)
4. Simulation Results and Discussions
This study has investigated MIMO systems performance metrics in terms of error probability and the information theoretic capacity of the systems. Simulations were developed in MATLAB®. Each performance metrics is discussed in each sub-section that follows.
4.1. Channel Capacity Evaluation
By information theory, capacity is the upper bound on the information rate for error-free communication. Furthermore, in communication systems, high system capacity implies ability to have greater throughput than the low system capacity. In this work, simulations are implemented for the realization of the flat Rayleigh channel matrix to determine the ergodic capacity using quadrature phase shift keying (QPSK) because of its relative low bit error rate (BER). The capacities of the MIMO system with and without CSI are investigated. Figure 2 depicts ergodic channel capacity for MIMO system with different antenna configurations in flat Rayleigh channel. It is observed that the capacity with full CSI at the transmitter is higher than the capacity without CSI at low average SNR.
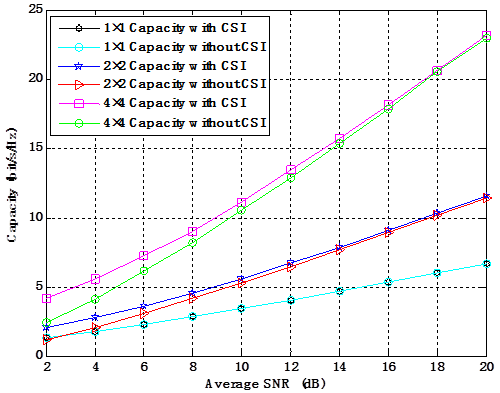
Figure 2. Ergodic channel capacity for MIMO system with different antenna configurations in flat Rayleigh channel.
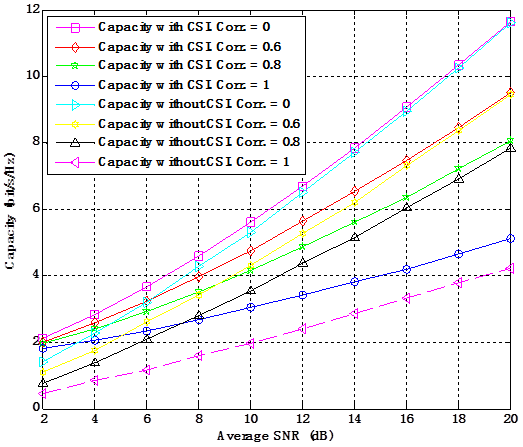
Figure 3. Ergodic channel capacity for 2×2 system with and without CSI for different level of correlation at both ends of the link in flat Rayleigh channel.
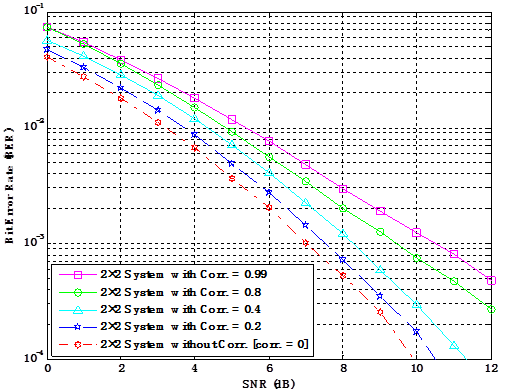
Figure 4. BER Performance for 2×2 system for different level of correlation at both ends of the link in flat Rayleigh channel.
The capacity of MIMO system with correlation at both sides of the link is compared using the correlation model. Figure 3 illustrates the ergodic channel capacity for 2×2 system with and without CSI for different level of correlation at both ends of the link in flat Rayleigh channel. It is observed that the capacity with full CSI at the transmitter is higher than without CSI for the whole range of average SNR. This implies that availability of CSI at the transmitter can enhance MIMO system performance significantly. It is also observed that the higher the correlation the higher the difference in capacity of the systems. This shows that MIMO system capacity depends on the spatial correlation of the channels which results in degradation of the ergodic capacity of the system. The capacity with full CSI at the transmitter is higher because water-filling approach was employed to adaptively allocate more power to stronger subchannels to enhance their capacity. This is not so in the transmitter without CSI as equal power is applied to all subchannels, which leads to loss in capacity due to wasted energy in the bad eigenmodes.
4.2. BER Evaluation
In digital transmission, the number of bit errors is the number of received bits of a data stream over communication channels that have been altered due to noise, interference, distortion or bit synchronization errors. The bit-error-rate (BER) performance of a receiver is a figure of merit that allows different systems to be compared in a fair manner. In addition, the BER is the fundamental performance measure of a system, quantifying the reliability or integrity of a received signal [19]. Hence, the performance of a system with low BER is better compared with the one with high BER.
Figure 4 shows the BER performance for a 2×2 system for different level of correlation at both ends of the link in Rayleigh channel. For instance, to achieve a BER of 10-3 for a system with zero correlation, about 7-dB SNR is needed. However, about 9.6-dB SNR is required to achieve the same BER for a system with 0.8 correlation -- meaning that an increase of 2.6 dB in signal power would be required to achieve the same BER of 10-3 as the system with zero correlation. Therefore, it is established that the higher the correlation, the higher the bit error rate. This shows that correlation hinders system performance.
5. Conclusions
In this paper, the effect of signal correlation for MIMO system in flat Rayleigh channel has been investigated. The simulation results show that capacity increases as signal correlation decreases while bit error rate increases with increase in signal correlation. Furthermore, it is found that in the correlated channel, the capacity with full CSI at the transmitter is higher than without CSI for the whole range of average SNR and that the higher the correlation the higher the difference in capacity of the systems. Therefore, as the channel becomes progressively correlated in space, the probability of multiplexing gain for the MIMO communication system reduces considerably.
References
- D. Gesbert, H. Bölcskei, D. A. Gore, and A. J. Paulraj, "Outdoor MIMO Wireless Channels: Models and Performance Prediction", IEEE Transactions on Communications, vol. 50, no. 12, pp. 1926-1934, 2002.
- P. Kyritsi, D. C. Cox, R. A. Valenzuela, and P. W. Wolniansky, "Correlation Analysis Based on MIMO Channel Measurements in an Indoor Environment", IEEE Journal on Selected Areas in Communications, vol. 21, no. 5, pp. 713- 720, 2003.
- S. K. Jha, M.K. Jain, "Performance Analysis of MIMO Systems using OSTBCs", International Journal of Engineering Trends and Technology.vol. 4,issue7, pp. 2860-2869, 2013
- P. Satyanarayana, M. A. Babu, H. Khan, M. Mallikarjun, "Performance Analysis of MIMO Systems using Orthogonal Space Time Coding over Rayleigh Fading Channel", International Journal of Modern Engineering Research, vol.2, issue.2, pp-283-287, 2012.
- A. Sridhar, B. L. Prakash, M. A. Yaseen, P. Rayi, "Performance and Evaluation of Space Time Block Codes in MIMO WideBandchannel Capacity", International Journal of Science and Advanced Technology, vol. 1 no. 6, pp. 253-258, 2011.
- E. Telatar, "Capacity of Multi-antenna Gaussian Channels," European Transactions on Telecommunications, vol. 10, no. 6, pp. 585–595, 1999.
- D.-S. Shiu, G. J. Foschini, M. J. Gans, and J. M. Kahn, "Fading Correlation and its Effect on the Capacity of Multi-element Antenna Systems," IEEE Trans. Commun., vol. 48, pp. 502–513, 2000.
- G. Tsoulos, MIMO System Technology for Wireless Communications, CRC Press, 2006.
- M. Vu, and A. Paulraj, "Optimal Linear Precoders for MIMO Wireless Correlated Channels With Nonzero Mean in Space–Time Coded Systems", IEEE Transactions on Signal Processing, vol. 54, no. 6, pp. 2318-2332, 2006.
- P. Xia, S. Zhou, and G. B. Giannakis, "Adaptive MIMO-OFDM Based on Partial Channel State Information", IEEE Transactions on Signal Processing, vol. 52, no. 1, pp. 202- 213, 2004.
- J. H. Kotecha and A. M. Sayeed, "Transmit Signal Design for Optimal Estimation of Correlated MIMO Channels, IEEE Transactions on Signal Processing", vol. 52, no. 2, pp. 546-557, 2004.
- X. Xiaowei, W. Dexiao, G. Shuhong, "The study of MIMO channel correlation coefficient in the rainfall environment for satellite communications," 2013 IEEE 5th International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications, pp.378-382, 2013.
- H. Xuemin, W. Cheng-Xiang, J. Thompson, B. Allen, W.Q. Malik, G. Xiaohu, "On Space–Frequency Correlation of UWB MIMO Channels," IEEE Transactions on Vehicular Technology, vol.59, no.9, pp.4201-4213, 2010.
- M. Matthaiou, M.R. McKay, P.J. Smith, J.A. Nossek, "On the condition number distribution of complex wishart matrices", IEEE Transactions on Communications, vol.58, no.6, pp.1705-1717, 2010 H. D. Tuan, H. H. Kha, H. H. Nguyen and V. J. Luong, "Optimized Training Sequences for Spatially Correlated MIMO-OFDM", IEEE Transactions on Wireless Communications, vol. 9, no. 9, pp. 2768-2778, 2010.
- D. Gesbert, M. Shafi, D. S. Shiu, P. Smith, and A. Naguib, "From theory to practice: An overview of MIMO space-time coded wireless systems," IEEE Journal on Selected Areas in Communications, vol. 21, no. 3, pp. 281–302, 2003.
- C. X. Wang, X. Hong, H. Wu, and Wen Xu, "Spatial-Temporal Correlation Properties of the 3GPP Spatial Channel Model and the Kronecker MIMO Channel Model", EURASIP Journal on Wireless Communications and Networking, vol.2007, issue 1, pp. 59-59, 2007.
- I. A. Alimi, J. J. Popoola, K. F. Akingbade, and M. O. Kolawole, "Performance Analysis of Bit-Error-Rate and Channel Capacity of MIMO Communication Systems over Multipath Fading Channels", International Journal of Informatics and Communication Technology. vol.2, no.2, pp. 57-63, 2013.
- I. Ali, "Bit-Error-Rate (BER) Simulation Using MATLAB, International Journal of Engineering Research and Applications", vol. 3, issue 1, pp.706-711, 2013.
- J. P. Kermoal, L. Schumacher, K. I. Pedersen, P. E. Mogensen, and F. Frederiksen, "A Stochastic MIMO Radio Channel Model With Experimental Validation", IEEE Journal on Selected Areas in Communications, vol. 20, no. 6, pp.1211-1226, 2002.
- H.J. Song, A. Bekaryan, J.H. Schaffner, A. Hussain, P.S. Kildal, "Effects of Mutual Coupling on LTE MIMO Capacity for Monopole Array: Comparing Reverberation Chamber Tests and Drive Tests," Antennas and Wireless Propagation Letters, IEEE , vol.14, no., pp.454,457, 2015
Bibliography
|
|
|
|
|
|
|
|







