H-crystal as a Core Structure in Multilayer Weighted Networks
Simon S. Li1, 2, Xia Lin3, Xiaozhong Liu4, Fred Y. Ye1, 2,*
1School of Information Management, Nanjing University, Nanjing, China
2Jiangsu Key Laboratory of Data Engineering and Knowledge Service, Nanjing, China
3College of Computing and Informatics, Drexel University, Philadelphia, USA
4School of Informatics and Computing, Indiana University, Bloomington, USA
Abstract
Extending the network h-core in single layer weighted networks, a method to extract a multilayer weighted network’s core structure, called h-crystal, has been proposed and verified. By applying the algorithms of h-degree and h-strength to each individual layer, a network’s h-core consisting of all the nodes having the h-degree above within edges and an h-subnet consisting of all the edges having the h-strength above with the nodes adjacent to the edges had been obtained, for each layer, at first. H-crystal is then identified by constructing layer-bridges between the layers’ network h-cores and h-subnets. Via two empirical cases of information networks, it is found that the h-crystals of the networks exist, while their features and properties are revealed.
Keywords
H-degree, H-strength, Network H-core, H-subnet, H-crystal, Multilayer Networks, Weighted Network, Information Network, Heterogeneous Network
Received: June 12, 2016
Accepted: June 27, 2016
Published online: July 21, 2016
@ 2016 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY license. http://creativecommons.org/licenses/by/4.0/
1. Introduction
Stimulated by Watts & Strogatz [1] and Barabási & Albert [2] among others, the term complex networks became a household word among the 21th century scientists, leading to new developments in network (i.e. graph) theory, dynamics of networks, social networks, ecological networks, infrastructure related networks, molecular networks, spatial scientometrics, informetrics, webometrics as well as cognitive networks [3-9].
While most studies of classical complex networks focus on single-layer networks [6, 10], new research on complex networks often focuses on multilayer networks [11-12], multiplex network [13-15], and hierarchical and heterogeneous networks [7-9]. In the long review of Boccaletti et al. [12], the characteristics of a multilayer network had been defined, where a graph G with different layers ![]() and
and ![]() had common elements as interconnections. Then a multiplex network was defined as a special type of multilayer network.
had common elements as interconnections. Then a multiplex network was defined as a special type of multilayer network.
Meanwhile, the classical homogeneous scholarly graph contains one type of nodes only, either author nodes, keyword nodes, or document nodes. The heterogeneous scholarly graph, on the other hand, characterizes the complex relations between different kinds of nodes, and various types of paths provide great potential to interconnect different research objects, i.e., publications, terms, authors, venues, etc. [16-20], which enriched the studies of multilayer heterogeneous networks.
Moreover, after h-index was introduced [21], its applications in homogeneous networks have been discussed [22]. In our early work, we have extended the h-index to h-degree, h-strength and h-subnets [23-25], to reveal network properties and core structures. In this paper, we continue extending the h-type terminology to multilayer (and heterogeneous) networks, which may apply to reveal the core structure of multilayer weighted networks, address the core documents and look potential applications in three-dimensional (3D) visualization.
In this research, we focus on the multilayer weighted networks and translate the h-type concepts and methods from single-layer networks to multilayer networks. In Particular, we proposed and studied a new multilayer core, h-crystal, for investigating core structure and context in the multilayer weighted networks. While similarity method was used to explore "core documents" [26-28] in single-layer (and homogeneous) networks, h-crystal can be a new method to identify another kind of core structures in multilayer (and heterogeneous) networks.
2. Methodology
It is well known that a network or graph consists of nodes and edges (links) [6,29,30]. When nodes and edges represent information-related objects, we refer to such networks as information networks. Figure 1 shows some objects used to build information networks in scientific literature, and different objects and edges may belong to different types.

Fig. 1. Information network relations in document.
Co-authorship networks, co-citation networks, bibliographic coupling networks and similar networks are examples of (homogeneous) single-layer networks, which host only the same kind of information. Now, following Boccaletti et al. [12], we consider several aspects simultaneously, leading to a multilayered structure. For example, we may consider the three layers illustrated in Figure 2: a co-citation layer, a bibliographic coupling layer and a co-keyword layer, which can be integrated into a multilayered graph within more scholarly information, comparing with single-layer network. This construction is an example of a multilayer network in which constituents, i.e. nodes and edges, are consist of different layers. In these examples nodes are papers (layers 1 and 2) and terms (layer 3), while edges have different meanings as well, namely referring to co-citation, bibliographic coupling and being co-keywords.
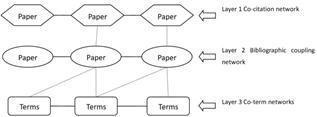
Fig. 2. An example of a multilayer information network.
In the following sections, along the h-type core structure in the single-layer networks, we extend h-type concepts from the single-layer networks to the multilayer networks.
2.1. Characterizing and Measuring the Core Structure of Single-Layer Network
Taking the lead from Hirsch’s h-index [21] we introduced the notions of h-degree, for nodes, and h-strength, for edges [23-25]. These notions can be used to characterize weighted networks.
Definition 1 [23]. The h-degree (dh) of node n in a weighted network is equal to dh(n) if dh(n) is largest natural number such that node n has at least dh(n) links each with strength at least equal to dh(n).
Using the notion of an h-degree leads to a network’s h-core, a substructure of the complete network.
Definition 2. A network’s h-core is set of nodes and their links, that all have an h-degree at least h.
It is important to point out that the h-degree (dh) is a node-based measure, while a network’s h-core is a set of the nodes and their links.
The h-strength is also introduced as follows [25]:
Definition 3. The h-strength (hs) of a network is equal to hs, if hs is the largest natural number such that there are hs links each with strength at least equal to hs in the network.
The h-strength characterizes the core edges of a network in terms of link strengths. Dually to the notion of network’s h-core we now define the h-subnet.
Definition 4. The h-subnet of a network is a sub-network consisting of all edges with strengths larger than or equal to the h-strength of the network and the nodes adjacent to these edges.
Note that h-strength (hs) is a measure defined on edges and h-subnet includes all the edges and their nodes. The h-strength is an edge-based measure, while h-subnet is a set of the edges and their nodes. All these informetric indicators characterize the importance of the nodes within one layer.
A simple numbered example for identifying the network’s h-core and the h-subnet in a single-layer weighted network can be explained as shown as Figure 3.
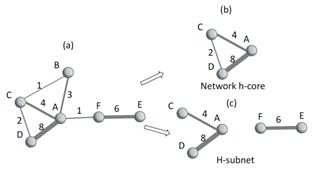
Fig. 3. A numbered example of network’s h-core and h-subnet in single-layer network.
In Figure 3, the graph (a) is a weighted network within 6 nodes, where each node has its h-degree as A:3, B:1, C:2, D:2, E:1 and F:1 so that the subgraph (b) consisted by the nodes with h-degree ≥ 2 as well as their links yields the network’s h-core, while the weights of 7 edges in the graph (a) rank as 8, 6, 4, 3, 2, 1, 1 and lead the h-strength equaling to 3 so that all edges with weights ≥ 3 generates h-subnet, i.e. subgraph (c).
2.2. Characterizing and Measuring the Core Structure of a Multilayer Network
It is necessary and important to find the core structure or sub-structure of a complex multilayer network [8], for judging the relatively important nodes and edges as well as their functions in the multilayer network. For the aim, we first introduce the notion of a layer bridge to connect the core structures of all single-layer networks so that we can approach the core structure of the multilayer network.
Definition 5. If two nodes in two layers of a multilayer network represent the same object, these nodes are artificially linked, which are called layer-bridges of the multilayer network.
When two layers in a multilayer network have layer-bridges they are connected, otherwise, they are not. The network’s h-core and the h-subnet are sub-structures of single-layer weighted networks, which might not be connected. When all layers are connected through layer-bridges, this may lead to the complete connected graph of the multilayer network.
Combing h-degree, h-strength with layer-bridges, linking through multilayer network’s h-cores and h-subnets, a core structure of whole multilayer weighted network, called h-crystal, is defined as follows.
Definition 6. The h-crystal is a core structure existing in a multilayer weighted network which consists of all network’s h-cores and h-subnets in each layer of the network, connected by layer-bridges between two layers.
By definition, an h-crystal is a core structure, linking through network’s h-cores and h-subnets in all layers via layer-bridges, where h-crystal must be connected. If there is only unconnected or broken structure, we say that h-crystal does not exist in the multilayer weighted network. Here, the layer-bridges between two layers link the really same nodes (same documents). As the h-core and h-subnet among single-layer networks are connected by the bridges, h-crystal will be connected and lead unique core structure in the multilayer weighted network so long as h-crystal exists.
A simple numbered example for identifying the h-crystal in a multilayer weighted network can be explained as shown as Figure 4.
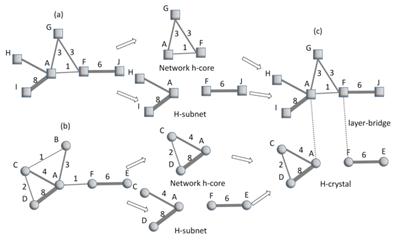
Fig. 4. A numbered example of h-crystal in multilayer network.
In Figure 4, both the graph (a) and graph (b) are weighted networks, respectively, within 6 nodes, which construct a two-layer network, where there are two same nodes (A and F). After computing and formulating the network’s h-cores and h-subnets of (a)-layer and (b)-layer similarly to Figure 3, the h-crystal can be generated by connecting same A and F as layer-bridges.
It is noted that there are only few methods for extracting network core in a complex network. In homogeneous single-layer networks, we can mention k-core [31] and backbone [8]. However, the methods focus on node degree and cannot be applied to multilayer weighted networks. Here, we compute k-cores in each layer and put them together as a comparison. As both k-core and backbone need artificial parameters for approaching results, in which we cannot determine the changeable parameter α for backbone and we may set k=h for extracting k-core according to node degree, we compare with k-core only.
2.3. The Procedure of Identifying H-crystal
In next empirical studies, a multilayer network is constructed by a co-citation layer, a bibliographic coupling layer and a co-keyword layer, where the h-crystal of the multilayer network can be identified as three steps as illustrated in Figure 5, in the weighted network.
Step 1: Extracting the network’s h-core using the algorithm of h-degree in each layer;
Step 2: Finding the h-subnet using the algorithm of h-strength in each layer;
Step 3: Constructing layer-bridges through linking the same nodes in two layers.
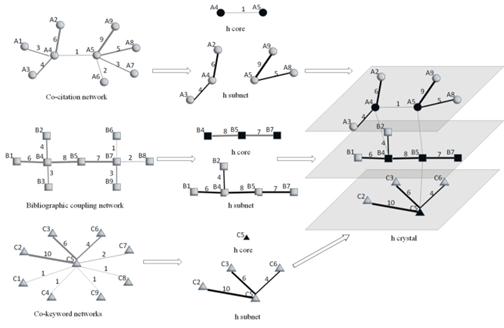
Fig. 5. Identifying the h-crystal in a multilayer network.
The dark black nodes and edges in Figure 5 mark the network’s h-core, and the white nodes with edges form the h-subnet. The same paper nodes in Layer 1 and Layer 2 construct layer-bridges between Layer 1 and Layer 2, and the same keywords in different papers in Layer 2 and Layer 3 produce layer-bridges between Layer 2 and Layer 3. As the co-citation layer, bibliographic coupling layer and co-keyword layer are linked by layer-bridges, we got connected h-crystal.
Pseudocodes for identifying h-crystal in a multilayer network are provided in Appendix 1. While we draw 2D diagram with using the open-source software packages NetDraw (cf. https://sites.google.com/site/netdrawsoftware/home), we prefer to create 3D diagram with using Mage (cf. http://kinemage.biochem.duke.edu/software/mage.php), for clear crystal effects and potential 3D visualization developments.
3. Empirical Studies
Practical experiments have been run to test the above method of identifying h-crystal in a multilayer network.
3.1. Datasets and Experiments
Two sets of data were generated from the Web of Science (WoS) for the experiment:
(1) The document set referred to as the "h-set", which is retrieved from the Web of Science (WoS) by the following search strategy: TS= (h-index OR h-type ind* OR h-like ind* OR Hirsch index) OR TI="An index to quantify*" in the WoS for the publication period 2005-2012. Results were restricted to the two fields Information Science & Library Science and Multidisciplinary Sciences.
(2) The document set referred to as the "GR&SM-set", which is retrieved by the search strategy: TS= (General relativity) AND TS=(Standard model) in the database SCI-E for the publication period 1915-2012, without other restrictions.
The data sets were downloaded on August 1, 2014.
These two data sets represent two multilayer information networks with a combination of a co-citation network, a bibliographic coupling network and a co-keyword network (including the keywords in the ID and DS records). Tables 1 and 2 show the main features of these multilayer weighted networks.
Table 1. Multilayer weighted network parameters of the "h-set".
| Type | Co-citation network | Bibliographic coupling network | Co-keyword network |
| number of nodes | 6614 | 484 | 1237 |
| number of edges | 467,151 | 89,123 | 11,718 |
| h-degree | 15 | 12 | 8 |
| number of nodes in the network’s h core | 20 | 23 | 14 |
| h-strength | 40 | 27 | 21 |
| number of nodes in the network’s h core and h subnet | 27 | 38 | 20 |
| number of edges in the network’s h core and h subnet | 199 | 263 | 103 |
Table 2. Multilayer weighted network parameters of the "GR&SM-set".
| Type | Co-citation network | Bibliographic coupling network | Co-keyword network |
| number of nodes | 22,434 | 625 | 2142 |
| number of edges | 1,684,501 | 22,972 | 20,563 |
| h-degree | 10 | 12 | 7 |
| number of nodes in the network’s h core | 17 | 15 | 8 |
| h-strength | 20 | 35 | 15 |
| number of nodes in the network’s h core and h subnet | 21 | 36 | 11 |
| number of edges in the network’s h core and h subnet | 105 | 85 | 34 |
3.2. The H-crystal of the "H-set"
The h-crystal identified by the h-crystal procedure for the "h-set" is shown in Figure 6, where A refers to the co-citation layer, B to the bibliographic coupling layer and C to the co-keyword layer. Linked nodes between layers A and B represent the same papers, i.e. A270=B195, and so on.
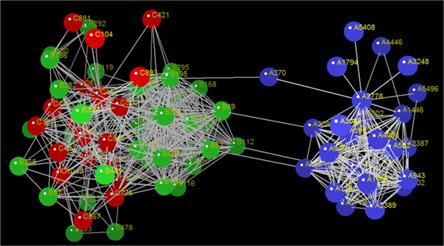
Fig. 6. H-crystal of the dataset "h-set".
In Figure 6, the A-type nodes express the core nodes of the co-citation network (A-core); B-type nodes mark the core nodes of the bibliographic coupling network (B-core), while C-type nodes refer to the core nodes of the co-keyword network (C-core). To illustrate the network structural information, we select the top five core nodes and rank according to their betweenness centralities, shown in Table 3, which form the core of the multilayer weighted network.
Table 3. Top 5 core nodes by betweenness centrality (denoted as bc) in the h-crystal of the "h-set".
| Layer of co-citation network | Layer of bibliographic coupling network | Layer of co-keyword network | |||
| Core node | bc | Core node | bc | Core node | bc |
| A4063 | 0.46 | B296 | 0.1934 | C462 | 0.5439 |
| A2778 | 0.3569 | B116 | 0.0713 | C493 | 0.5234 |
| A2387 | 0.2985 | B53 | 0.043 | C547 | 0.1345 |
| A1802 | 0.0554 | B120 | 0.0368 | C440 | 0.0673 |
| A1446 | 0.0554 | B391 | 0.0345 | C1045 | 0.0497 |
All these core nodes can be observed in Figure 6.
3.3. The H-crystal of "GR&SM-set"
Applying the h-crystal procedure to the "GR&SM-set", a similar h-crystal can be created and shown in Figure 7, where 3D-visual graphs are given, with similar A, B, C layers and symbols as in the previous example.
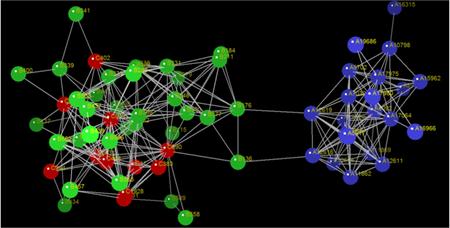
Fig. 7. H-crystal of the dataset "GR&SM-set".
Similarly, we list in Table 4 the top five core nodes according to their betweenness centrality. They form the core of the network core in the multilayer weighted network.
Table 4. Top 5 core nodes by betweenness centrality (bc) in the h-crystal of the "GR&SM-set".
| Layer of co-citation network | Layer of bibliographic coupling network | Layer of co-keyword network | |||
| Core node | bc | Core node | bc | Core node | bc |
| A17064 | 0.4363 | B436 | 0.1914 | C890 | 0.3667 |
| A7032 | 0.1962 | B330 | 0.1805 | C448 | 0.2444 |
| A17975 | 0.1224 | B331 | 0.1227 | C838 | 0.2 |
| A5702 | 0.1221 | B503 | 0.0426 | C351 | 0.1778 |
| A12620 | 0.1198 | B377 | 0.0319 | C2031 | 0.0667 |
Again, all these core nodes can easily be observed in the visual representations in Figure 7.
As a comparison, we also list the total numbers of nodes of both h-crystal and k-core in two datasets, as shown in Table 5, in which the k-core is calculated by k-core function in the software package Networkx (https://networkx.github.io), with setting k=h-degree in each layer then summing the nodes of all layers together. Here, the A, B, C three layers’ k-cores of dataset ‘h-set’ contain nodes as 6222, 471, 924 when k=15, 12, 8 respectively, with same nodes between A and B as 288, so that the total nodes of k-core become 6222+471+924-288=7329. Similarly, the A, B, C three layers’ k-cores of dataset ‘GR&SM-set’ contain nodes as 22345, 530, 1888 when k=10, 12, 7 respectively, with same nodes between A and B as 95, so that the total nodes of k-core are 22345+530+1888-95=24668.
Table 5. Total nodes of the h-crystal and k-core.
| Dataset "h-set" | Dataset "GR&SM-set" | ||
| Nodes of h-crystal | Nodes of k-core | Nodes of h-crystal | Nodes of k-core |
| 81 | 7329 | 66 | 24668 |
| Node percentage of h-crystal vs. k-core (%) | Node percentage of h-crystal vs. k-core (%) | ||
| 1.1 | 0.26 | ||
Comparing the nodes in h-crystal and k-core, we find that all nodes of h-crystal are covered by the nodes of k-core (while k=h-degree), which means h-crystal is real core. However, h-crystal is much smaller (only about 1% nodes of k-core) and k-core may be unconnected, so that h-crystal may become the minimum connected core in a multilayer weighted network.
The above two empirical cases demonstrate that an ‘h-crystal’ can be identified in real-world multilayer information networks and h-crystal can form the core structure of a multilayer weighted network, which could lead to effective applications for extracting and judging important core. The documents of the core nodes of the A- and the B-layer are listed in Appendices 2 and 3. It is clear that those nodes provide the key information for the constructed multilayer networks. For example, the first ranked items at the A-layers are Hirsch’s original article (A2778) introducing the h-index in "h-set" and Reiss et al.’s famous paper (A17975) on the accelerating universe that led to the 2011 Nobel Prize in physics, which are really the most important documents.
4. Analysis and Discussion
As the h-crystal consists of core nodes (nodes in the network’s h-core), core edges (edges in the h-subnet) in each single-layer weighted networks, and layer-bridges in-between two layers, we can derive some of their theoretical properties following the ideas of an h-degree and h-strength [23-25]. Actually, the analytical properties of h-crystal can be obtained by merging all the layers’ network’s h-cores and h-subnets, where network’s h-cores generated by nodes following h-degree algorithm and h-subnets by edges following h-strength algorithm. However, as there is complex mathematical structure in multilayer networks [11], a general result has not yet been reached.
4.1. The Nodes of the H-crystal
Consider a multilayer weighted network consisting of three layers A, B and C, with NA, NB and NC nodes, and the three layers have the h-degree NAh, NBh and NCh, respectively. Suppose that the numbers of nodes that the node’s h-degree equals NAh, NBh and NCh are NAd, NBd and NCd respectively. Let NAh-cs, NBh-cs and NCh-cs represent number of nodes in the network’s h-core and h-subnet, NAh-s, NBh-s and NCh-s denote nodes in the h-subnet only (except nodes in the network’s h core). If the number of same nodes of NAh and NBh is NAB and that of NBh and NCh is NBC, the total number of nodes in the h-crystal (Nh-crystal) can be calculated by following formulas
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
In our examples, we find that the Nh-crystal=27+38+20 -4-0=81 for the "h-set" and Nh-crystal=21+36+11 -2-0=66 for ‘GR&SM-set’, theoretically.
If the total number of nodes N = NA + NB + NC and Nh= NAh +NBh +NCh, in which node i has degree di, with h-degree hi, we get
![]() (7)
(7)
![]() (8)
(8)
 (9)
(9)
This means that Nh-crystal is restricted by N and Nh.
4.2. The Edges of the H-crystal
Suppose that a multilayer weighted network consists of three layers A, B and C, with number of edges LA, LB and LC respectively, each with h-strength LAh, LBh and LCh and the numbers of edges for which the edge’s h-strength equals LAh, LBh and LCh are LAd, LBd and LCd respectively. Let LAh-cs, LBh-cs and LCh-cs represent number of edges in the network’s h-core and h-subnet. If the number of links of two layers A, B is LAB and that of two layers B, C is LBC, the total number of edges of the h-crystal (Lh-crystal) is:
![]() (10)
(10)
In our cases, for ‘h-set’, the Lh-crystal=199+263+103+0+207=772; for ‘GR&SM-set’, Lh-crystal=105+85 +34 +0+96=320.
If the total number of edges L= LA + LB + LC and Lh= LAh +LBh +LCh, with weights sj in edge j and![]() , we obtain
, we obtain
![]() (11)
(11)
 (12)
(12)
where ![]() is the sum of the total weight of all edges in the network and L indicates total edges.
is the sum of the total weight of all edges in the network and L indicates total edges.
It is worth to point out that our results show general ways to reach the core structure of both multilayer and heterogeneous networks, as the h-crystal covers heterogeneous structure (where co-keyword is different from co-citation and bibliographic coupling), though the three layers belong to homogeneous layer each respectively.
4.3. Potential Applications
The h-crystal revealed a core structure in a multilayer weighted network, which could be useful in three-dimensional (3D) visualization. In a complex network, it is impossible to show all nodes and edges in visualization, so that it is important to find and show the core nodes and edges. The h-crystal provides a potential way to approach the core structure in weighted networks, so that it may be meaningful in future studies.
Meanwhile, the h-crystal can tell the most significant core objects in a multilayer (and heterogeneous) graphical environment, so that it may reveal important core information.
4.4. Limitation of H-crystal
In this paper, we show only how h-crystal can be defined and constructed in a multilayer weighted network. As there are complex cases for different constitutes of h-crystals (such as different choice of layers), we have not attempted to provide a mathematical proof for the generalizability of the h-crystal. Also, although we tried various centralities, we only chose betweenness centrality for showing typical comparison and k-core for core comparison.
More researches will need to be done to validate and extend the h-crystal method to general multilayer (and heterogeneous) networks in future.
5. Conclusion
In this paper, a new method to find a core structure in a multilayer weighted network of information, called h-crystal, has been introduced. The core structure represents the most significant nodes and edges in the network thus this method can be applied to simplify multilayer weighted networks. Moreover, the h-crystal integrates core nodes and edges of the multilayer weighted network, for which important information of the multilayer weighted network can be obtained.
Other core structures may exist in multilayer and heterogeneous weighted networks, depending on the operationalization of the notion of a core. Yet, h-crystal can be considered a basic one and it has highly simplified efficiency. Like all the other h-type measures, h-crystal will be an efficient method for identifying and selecting objects from large information. A potential application of h-crystal, which we are currently working on, is a retrieval system with 3D visualization displays. The h-crystal-based system will show the retrieved document set in 3D with the core documents highlighted and with interactions to allow the user to interact with the 3D structure of the whole h-crystal.
Although multilayer weighted information networks are only one kind of multilayer weighted networks, the h-crystal methodology can be generalized to other types of weighted networks. Currently, our case study addresses only undirected multilayer weighted information networks, leaving directed multilayer as well as heterogeneous weighted networks for future investigations. Also, the dynamical issues leave for future works.
Acknowledgements
We acknowledge the financial support from the National Natural Science Foundation of China Grant No 71173187 and the Jiangsu Key Laboratory Fund, thank Dr. Ronald Rousseau and Dr. Ludo Waltman as well as anonymous reviewers, for their helpful comments.
Appendix 1: Pseudocodes of the H-crystal Algorithm
Algorithm1 generate bibliographic coupling network
Input: the record data of WoS
Output: bibliographic coupling network and the node information
Initialize the empty bibliographic coupling network
Initialize the sparse matrix M
for each record r in the record data of WoS do
for each reference c in the record r do
Mßadd the ID of the record r, the ID of the reference c and 1
the node informationßadd the node information of the record
end for
end for
MßM * M.T
for each nonzero element aij in M do
bibliographic coupling networkßadd i, j, aij into the Graph
end for
Return bibliographic coupling network, the node information
Algorithm2 generate co-citation network
Input: the record data of WoS
Output: co-citation network and the node information
Initialize the empty co-citation network
for each record in the record data of WoS do
for the reference cj in the references of the record do
for the reference cj in the references of the record do
if i < j then
if the reference ci and the reference cj in the co-citation network then
the weight of edge between the reference ci and the reference cj <-1
elseif then
co-citation network ßadd the ID of reference ci, the ID of the reference cj and 1
the node informationßadd the node information of the reference
end if
end if
end for
end for
end for
Return co-citation network, the node information
Algorithm3 generate co-term network
Input: the content of ID and DE field in the record data of WoS
Output: co-term network and the node information
Initialize the empty co-term network
for each record in the record data of WoS do
for the term ti in the content of ID and DE field of the record do
for the term tj in the content of ID and DE field of the record do
if i < j then
if the term ti and the term tj in the co-term network then
the weight of edge about the term ti and the term tj <-1
elseif then
co-term network ßadd the ID of term ti, the ID of the term tj and 1
the node informationßadd the node information of the term
end if
end if
end for
end for
end for
Return co-term network, the node information
Algorithm4 compute h core and h subnet of each layer network
Input:G(bibliographic coupling network/co-citation network/co-term network)
Output: h core and h subnet of the corresponding network
Initialize the empty h core and h subnet of G
for each node n in G do
h degree of the node ß n has at least h(n) links each with strength at least equal to h(n)
end for
h degree of the Gß h index of h degree of every node in G
for each node n in G do
if h degree of node n >= h degree of the G then
h core of Gßadd node n into h core of G,meanwhile add the link if node n have a link with other nodes in h core of G
end if
end for
h strenth of the Gßh index of the strenth of every edge in G
for each edge e in G do
if the strength of edge e >= h strenth of the G then
h subnet of Gßadd edge e into h subnet of G
end if
end for
h core and h subnet of G ß combine h core of G with h subnet of G
Return h core and h subnet of G
Algorithm5 construct bridge relations between bibliographic coupling network and co-citation network
Input: h core and h subnet of bibliographic coupling network, h core and h subnet of co-citation network
Output: bridge relations between bibliographic coupling network and co-citation network
for each node ni in h core and h subnet of bibliographic coupling network do
for each node nj in h core and h subnet of co-citation network do
if ni equal nj then
bridge relations ßconstruct a link between node ni and node nj
end if
end for
end for
Return bridge relations between bibliographic coupling network and co-citation network
Algorithm6 construct bridge relations between bibliographic coupling network and co-term network
Input: h core and h subnet of bibliographic coupling network, h core and h subnet of co-term network
Output: bridge relations between bibliographic coupling network and co-term network
for each node ni in h core and h subnet of bibliographic coupling network do
for each node nj in h core and h subnet of co-term network do
if ni associated with nj then
bridge relations ßconstruct a link between node ni and node nj
end if
end for
end for
Return bridge relations between bibliographic coupling network and co-term network
Algorithm7 construct h crystal of heterogeneous weighted networks
Input: h core and h subnet of co-citation network, h core and h subnet of bibliographic coupling network, h core and h subnet of co-term network, bridge relations between bibliographic coupling network and co-citation network, bridge relations between bibliographic coupling network and co-term network
Output: h crystal of heterogeneous weighted networks
Initialize the empty graph(h crystal of heterogeneous weighted networks)
h crystal of heterogeneous weighted networks ß combine(h core and h subnet of co-citation network ,h core and h subnet of bibliographic coupling network, h core and h subnet of co-term network, bridge relations between bibliographic coupling network and co-citation network, bridge relations between bibliographic coupling network and co-term network)
if h crystal of heterogeneous weighted networks is connected then
h crystal of heterogeneous weighted networks is existing
end if
Return h crystal of heterogeneous weighted networks
Appendix 2 A- and B- Core Nodes in H-crystal of "H-set", Ranked by Total Citations (TC)
| ID | AU | TI | SO | PY | TC |
| A2778* | Hirsch, JE | An index to quantify an individual's scientific research output | PROCEEDINGS OF THE NATIONAL ACADEMY OF SCIENCES OF THE UNITED STATES OF AMERICA | 2005 | 1828 |
| A1802* | Egghe, L | Theory and practise of the g-index | SCIENTOMETRICS | 2006 | 440 |
| A4063* | Meho, LI; Yang, K | Impact of data sources on citation counts and rankings of LIS faculty: Web of science versus scopus and google scholar | JOURNAL OF THE AMERICAN SOCIETY FOR INFORMATION SCIENCE AND TECHNOLOGY | 2007 | 260 |
| A6002 | Van Raan, AFJ | Comparison of the Hirsch-index with standard bibliometric indicators and with peer judgment for 147 chemistry research groups | SCIENTOMETRICS | 2006 | 239 |
| A2779 | Hirsch, JE | Does the h index have predictive power? | PROCEEDINGS OF THE NATIONAL ACADEMY OF SCIENCES OF THE UNITED STATES OF AMERICA | 2007 | 226 |
| A943 | Braun, T; Glanzel, W; Schubert, A | A Hirsch-type index for journals | SCIENTOMETRICS | 2006 | 198 |
| A3092 | Jin, BH; Liang, LM; Rousseau, R; Egghe, L | The R- and AR-indices: Complementing the h-index | CHINESE SCIENCE BULLETIN | 2007 | 194 |
| A582 | Ball, P | Index aims for fair ranking of scientists | NATURE | 2005 | 174 |
| A671 | Batista, PD; Campiteli, MG; Kinouchi, O; Martinez, AS | Is it possible to compare researchers with different scientific interests? | SCIENTOMETRICS | 2006 | 173 |
| A1801 | Egghe, L; Rousseau, R | An informetric model for the Hirsch-index | SCIENTOMETRICS | 2006 | 154 |
| A857 | Bornmann, L; Daniel, HD | What do we know about the h index? | JOURNAL OF THE AMERICAN SOCIETY FOR INFORMATION SCIENCE AND TECHNOLOGY | 2007 | 156 |
| A1446* | Cronin, B; Meho, L | Using the h-index to rank influential information scientists | JOURNAL OF THE AMERICAN SOCIETY FOR INFORMATION SCIENCE AND TECHNOLOGY | 2006 | 141 |
| A863 | Bornmann, L; Mutz, R; Daniel, HD | Are there better indices for evaluation purposes than the h index? a comparison of nine different variants of the h index using data from biomedicine | JOURNAL OF THE AMERICAN SOCIETY FOR INFORMATION SCIENCE AND TECHNOLOGY | 2008 | 141 |
| A853 | Bornmann, L; Daniel, HD | Does the h-index for ranking of scientists really work? | SCIENTOMETRICS | 2005 | 135 |
| A270 | Alonso, S; Cabrerizo, FJ; Herrera-Viedma, E; Herrera, F | h-Index: A review focused in its variants, computation and standardization for different scientific fields | JOURNAL OF INFORMETRICS | 2009 | 136 |
| A3248 | Kelly, CD; Jennions, MD | The h index and career assessment by numbers | TRENDS IN ECOLOGY & EVOLUTION | 2006 | 124 |
| A1397 | Costas, R; Bordons, M | The h-index: Advantages, limitations and its relation with other bibliometric indicators at the micro level | JOURNAL OF INFORMETRICS | 2007 | 112 |
| A2389 | Glanzel, W | On the h-index - A mathematical approach to a new measure of publication activity and citation impact | SCIENTOMETRICS | 2006 | 101 |
| A940 | Braun, T; Glanzel, W; Schubert, A | A Hirsch-type index for journals | SCIENTIST | 2005 | 97 |
| A5408 | Schubert, A; Glanzel, W | A systematic analysis of Hirsch-type indices for journals | JOURNAL OF INFORMETRICS | 2007 | 92 |
| A5496 | Sidiropoulos, A; Katsaros, D; Manolopoulos, Y | Generalized Hirsch h-index for disclosing latent facts in citation networks | SCIENTOMETRICS | 2007 | 98 |
| A595 | Banks, MG | An extension of the Hirsch index: Indexing scientific topics and compounds | SCIENTOMETRICS | 2006 | 75 |
| A4446 | Oppenheim, C | Using the h-index to rank influential British researchers in information science and librarianship | JOURNAL OF THE AMERICAN SOCIETY FOR INFORMATION SCIENCE AND TECHNOLOGY | 2007 | 58 |
| A1794 | Egghe L | Power Laws in the Information Production Process: Lotkaian Informetrics | LIBR INFORM SCI SER | 2005 | 250 (Google scholar) |
| A1798 | Egghe L | An improvement of the H-index: the G-index | ISSI newsletter | 2006 | 267 (Google scholar) |
| A3088 | Jin B. | Scientists designed a new indicator for themselves: h-index | SCI FOCUS | 2006 | 54 (Google scholar) |
| A2387* | Glanzel W | A Discussion on the opportunities and limitations of h-index | SCI FOCUS | 2006 | 15 (Google scholar) |
| B49 | Jin, BH; Liang, LM; Rousseau, R; Egghe, L | The R- and AR-indices: Complementing the h-index | CHINESE SCIENCE BULLETIN | 2007 | 194 |
| B53* | Bornmann, L; Daniel, HD | What do we know about the h index? | JOURNAL OF THE AMERICAN SOCIETY FOR INFORMATION SCIENCE AND TECHNOLOGY | 2007 | 156 |
| B112 | Bornmann, L; Mutz, R; Daniel, HD | Are there better indices for evaluation purposes than the h index? a comparison of nine different variants of the h index using data from biomedicine | JOURNAL OF THE AMERICAN SOCIETY FOR INFORMATION SCIENCE AND TECHNOLOGY | 2008 | 141 |
| B195 | Alonso, S; Cabrerizo, FJ; Herrera-Viedma, E; Herrera, F | h-Index: A review focused in its variants, computation and standardization for different scientific fields | JOURNAL OF INFORMETRICS | 2009 | 136 |
| B297 | Egghe, L | The Hirsch Index and Related Impact Measures | ANNUAL REVIEW OF INFORMATION SCIENCE AND TECHNOLOGY | 2010 | 88 |
| B120* | Bar-Ilan, J | Informetrics at the beginning of the 21st century - A review | JOURNAL OF INFORMETRICS | 2008 | 81 |
| B402 | Bornmann, L; Mutz, R; Hug, SE; Daniel, HD | A multilevel meta-analysis of studies reporting correlations between the h index and 37 different h index variants | JOURNAL OF INFORMETRICS | 2011 | 52 |
| B104 | van Eck, NJ; Waltman, L | Generalizing the h- and g- indices | JOURNAL OF INFORMETRICS | 2008 | 45 |
| B118 | Jacso, P | Testing the calculation of a realistic h-index in Google Scholar, Scopus, and Web of Science for F. W. Lancaster | LIBRARY TRENDS | 2008 | 41 |
| B194 | Panaretos, J; Malesios, C | Assessing scientific research performance and impact with single indices | SCIENTOMETRICS | 2009 | 43 |
| B296* | Garcia-Perez, MA | Accuracy and Completeness of Publication and Citation Records in the Web of Science, PsycINFO, and Google Scholar: A Case Study for the Computation of h Indices in Psychology | JOURNAL OF THE AMERICAN SOCIETY FOR INFORMATION SCIENCE AND TECHNOLOGY | 2010 | 33 |
| B116* | Jacso, P | The pros and cons of computing the h-index using Web of Science | ONLINE INFORMATION REVIEW | 2008 | 25 |
| B186 | Bontis, N; Serenko, A | A follow-up ranking of academic journals | JOURNAL OF KNOWLEDGE MANAGEMENT | 2009 | 30 |
| B119 | Thelwall, M | Bibliometrics to webometrics | JOURNAL OF INFORMATION SCIENCE | 2008 | 27 |
| B107 | Egghe, L; Rao, IKR | Study of different h-indices for groups of authors | JOURNAL OF THE AMERICAN SOCIETY FOR INFORMATION SCIENCE AND TECHNOLOGY | 2008 | 19 |
| B282 | Franceschini, F; Maisano, D | The Hirsch spectrum: A novel tool for analyzing scientific journals | JOURNAL OF INFORMETRICS | 2010 | 17 |
| B295 | Norris, M; Oppenheim, C | The h-index: a broad review of a new bibliometric indicator | JOURNAL OF DOCUMENTATION | 2010 | 18 |
| B182 | Liu, YX; Rousseau, R | Properties of Hirsch-type indices: the case of library classification categories | SCIENTOMETRICS | 2009 | 18 |
| B480 | Schreiber, M; Malesios, CC; Psarakis, S | Exploratory factor analysis for the Hirsch index, 17 h-type variants, and some traditional bibliometric indicators | JOURNAL OF INFORMETRICS | 2012 | 17 |
| B399 | Kousha, K; Thelwall, M; Rezaie, S | Assessing the Citation Impact of Books: The Role of Google Books, Google Scholar, and Scopus | JOURNAL OF THE AMERICAN SOCIETY FOR INFORMATION SCIENCE AND TECHNOLOGY | 2011 | 18 |
| B403 | Zhang, L; Thijs, B; Glanzel, W | The diffusion of H-related literature | JOURNAL OF INFORMETRICS | 2011 | 14 |
| B292 | Serenko, A | The development of an AI journal ranking based on the revealed preference approach | JOURNAL OF INFORMETRICS | 2010 | 13 |
| B111 | Egghe, L | The Influence of transformations on the h-index and the g-index | JOURNAL OF THE AMERICAN SOCIETY FOR INFORMATION SCIENCE AND TECHNOLOGY | 2008 | 12 |
| B400 | Serenko, A; Dohan, M | Comparing the expert survey and citation impact journal ranking methods: Example from the field of Artificial Intelligence | JOURNAL OF INFORMETRICS | 2011 | 11 |
| B289 | Franceschini, F; Maisano, D; Perotti, A; Proto, A | Analysis of the ch-index: an indicator to evaluate the diffusion of scientific research output by citers | SCIENTOMETRICS | 2010 | 10 |
| B168 | Gagolewski, M; Grzegorzewski, P | A geometric approach to the construction of scientific impact indices | SCIENTOMETRICS | 2009 | 10 |
| B485 | Liu, JS; Lu, LYY | An Integrated Approach for Main Path Analysis: Development of the Hirsch Index as an Example | JOURNAL OF THE AMERICAN SOCIETY FOR INFORMATION SCIENCE AND TECHNOLOGY | 2012 | 11 |
| B110 | Bar-Ilan, J | The h-index of h-index and of other informetric topics | SCIENTOMETRICS | 2008 | 8 |
| B391* | Franceschini, F; Maisano, D | Bibliometric positioning of scientific manufacturing journals: a comparative analysis | SCIENTOMETRICS | 2011 | 8 |
| B368 | Jacso, P | The h-index, h-core citation rate and the bibliometric profile of the Scopus database | ONLINE INFORMATION REVIEW | 2011 | 6 |
| B493 | Jacso, P | Grim tales about the impact factor and the h-index in the Web of Science and the Journal Citation Reports databases: reflections on Vanclay's criticism | SCIENTOMETRICS | 2012 | 11 |
| B457 | Bornmann, L; Marx, W | HistCite analysis of papers constituting the h index research front | JOURNAL OF INFORMETRICS | 2012 | 5 |
| B117 | Rodriguez, V; Janssens, F; Debackere, K; De Moor, B | On material transfer agreements and visibility of researchers in biotechnology | JOURNAL OF INFORMETRICS | 2008 | 4 |
| B389 | Schreiber, M; Malesios, CC; Psarakis, S | Categorizing h-index variants | RESEARCH EVALUATION | 2011 | 4 |
| B478 | Jacso, P | Using Google Scholar for journal impact factors and the h-index in nationwide publishing assessments in academia - siren songs and air-raid sirens | ONLINE INFORMATION REVIEW | 2012 | 3 |
| B55 | Rodriguez, V; Janssens, F; Debackere, K; De Moor, B | On material transfer agreements and visibility of researchers in biotechnology | Proceedings of ISSI 2007: 11th International Conference of the International Society for Scientometrics and Informetrics, Vols I and II | 2007 | 5 |
| B373 | Jacso, P | The h-index, h-core citation rate and the bibliometric profile of the Web of Science database in three configurations | ONLINE INFORMATION REVIEW | 2011 | 1 |
| B378 | Kousha, K; Thelwall, M | Assessing the Citation Impact of Book-Based Disciplines: The Role of Google Books, Google Scholar and Scopus | PROCEEDINGS OF ISSI 2011: THE 13TH CONFERENCE OF THE INTERNATIONAL SOCIETY FOR SCIENTOMETRICS AND INFORMETRICS, VOLS 1 AND 2 | 2011 | 0 |
* asterisk signifies the top 5 core nodes.
Appendix 3 A- and B- Core Nodes in H-crystal of "GR&SM-set", ranked by Total Citations
| ID | AU | TI | SO | PY | TC |
| A17975* | Riess, AG; Filippenko, AV; Challis, P; Clocchiatti, A; Diercks, A; Garnavich, PM; Gilliland, RL; Hogan, CJ; Jha, S; Kirshner, RP; Leibundgut, B; Phillips, MM; Reiss, D; Schmidt, BP; Schommer, RA; Smith, RC; Spyromilio, J; Stubbs, C; Suntzeff, NB; Tonry, J | Observational evidence from supernovae for an accelerating universe and a cosmological constant | ASTRONOMICAL JOURNAL | 1998 | 7507 |
| A17064* | Perlmutter, S; Aldering, G; Goldhaber, G; Knop, RA; Nugent, P; Castro, PG; Deustua, S; Fabbro, S; Goobar, A; Groom, DE; Hook, IM; Kim, AG; Kim, MY; Lee, JC; Nunes, NJ; Pain, R; Pennypacker, CR; Quimby, R; Lidman, C; Ellis, RS; Irwin, M; McMahon, RG; Ruiz-Lapuente, P; Walton, N; Schaefer, B; Boyle, BJ; Filippenko, AV; Matheson, T; Fruchter, AS; Panagia, N; Newberg, HJM; Couch, WJ | Measurements of Omega and Lambda from 42 high-redshift supernovae | ASTROPHYSICAL JOURNAL | 1999 | 7022 |
| A19686 | Spergel, DN; Verde, L; Peiris, HV; Komatsu, E; Nolta, MR; Bennett, CL; Halpern, M; Hinshaw, G; Jarosik, N; Kogut, A; Limon, M; Meyer, SS; Page, L; Tucker, GS; Weiland, JL; Wollack, E; Wright, EL | First-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Determination of cosmological parameters | ASTROPHYSICAL JOURNAL SUPPLEMENT SERIES | 2003 | 6776 |
| A17980 | Riess, AG; Strolger, LG; Tonry, J; Casertano, S; Ferguson, HC; Mobasher, B; Challis, P; Filippenko, AV; Jha, S; Li, WD; Chornock, R; Kirshner, RP; Leibundgut, B; Dickinson, M; Livio, M; Giavalisco, M; Steidel, CC; Benitez, T; Tsvetanov, Z | Type Ia supernova discoveries at z > 1 from the Hubble Space Telescope: Evidence for past deceleration and constraints on dark energy evolution | ASTROPHYSICAL JOURNAL | 2004 | 2359 |
| A5702* | Copeland, EJ; Sami, M; Tsujikawa, S | Dynamics of dark energy | INTERNATIONAL JOURNAL OF MODERN PHYSICS D | 2006 | 2040 |
| A16966 | Peebles, PJE; Ratra, B | The cosmological constant and dark energy | REVIEWS OF MODERN PHYSICS | 2003 | 1962 |
| A7032* | Dvali, G; Gabadadze, G; Porrati, M | 4D gravity on a brane in 5D Minkowski space | PHYSICS LETTERS B | 2000 | 1805 |
| A5092 | Carroll, SM; Duvvuri, V; Trodden, M; Turner, MS | Is cosmic speed-up due to new gravitational physics? | PHYSICAL REVIEW D | 2004 | 1037 |
| A5617 | Colladay, D; Kostelecky, VA | Lorentz-violating extension of the standard model | PHYSICAL REVIEW D | 1998 | 964 |
| A15962 | Nojiri, S; Odintsov, SD | Modified gravity with negative and positive powers of curvature: Unification of inflation and cosmic acceleration | PHYSICAL REVIEW D | 2003 | 811 |
| A5616 | Colladay, D; Kostelecky, VA | CPT violation and the standard model | PHYSICAL REVIEW D | 1997 | 774 |
| A10798 | Hu, W; Sawicki, I | Models of f(R) cosmic acceleration that evade solar system tests | PHYSICAL REVIEW D | 2007 | 593 |
| A11862 | KOSTELECKY, VA; SAMUEL, S | SPONTANEOUS BREAKING OF LORENTZ SYMMETRY IN STRING THEORY | PHYSICAL REVIEW D | 1989 | 569 |
| A12619 | Kostelecky, VA | Gravity, Lorentz violation, and the standard model | PHYSICAL REVIEW D | 2004 | 423 |
| A12616 | Kostelecky, VA; Mewes, M | Signals for Lorentz violation in electrodynamics | PHYSICAL REVIEW D | 2002 | 343 |
| A12611 | Kostelecky, VA; Lehnert, R | Stability, causality, and Lorentz and CPT violation | PHYSICAL REVIEW D | 2001 | 313 |
| A11869 | KOSTELECKY, VA; POTTING, R | CPT, STRINGS, AND MESON FACTORIES | PHYSICAL REVIEW D | 1995 | 276 |
| A12608 | Kostelecky, VA; Lane, CD | Constraints on Lorentz violation from clock-comparison experiments | PHYSICAL REVIEW D | 1999 | 234 |
| A3910 | Buchert, T | On average properties of inhomogeneous fluids in general relativity: Dust cosmologies | GENERAL RELATIVITY AND GRAVITATION | 2000 | 224 |
| A16315 | Oyaizu, H; Lima, M; Hu, W | Nonlinear evolution of f(R) cosmologies. II. Power spectrum | PHYSICAL REVIEW D | 2008 | 126 |
| A12620* | Kostelecky, VA; Mewes, M | Lorentz and CPT violation in the neutrino sector | PHYSICAL REVIEW D | 2004 | 102 |
| B176 | Kostelecky, VA | Gravity, Lorentz violation, and the standard model | PHYSICAL REVIEW D | 2004 | 423 |
| B136 | Kostelecky, VA; Mewes, M | Signals for Lorentz violation in electrodynamics | PHYSICAL REVIEW D | 2002 | 343 |
| B152 | Brax, P; van de Bruck, C | Cosmology and brane worlds: a review | CLASSICAL AND QUANTUM GRAVITY | 2003 | 178 |
| B332 | Buchert, T | Dark Energy from structure: a status report | GENERAL RELATIVITY AND GRAVITATION | 2008 | 188 |
| B434 | Iocco, F; Mangano, G; Miele, G; Pisanti, O; Serpico, PD | Primordial nucleosynthesis: From precision cosmology to fundamental physics | PHYSICS REPORTS-REVIEW SECTION OF PHYSICS LETTERS | 2009 | 165 |
| B436* | Maartens, R; Koyama, K | Brane-World Gravity | LIVING REVIEWS IN RELATIVITY | 2010 | 152 |
| B282 | Tsujikawa, S | Matter density perturbations and effective gravitational constant in modified gravity models of dark energy | PHYSICAL REVIEW D | 2007 | 119 |
| B377* | Kostelecky, VA; Mewes, M | Electrodynamics with Lorentz-violating operators of arbitrary dimension | PHYSICAL REVIEW D | 2009 | 126 |
| B248 | Bailey, QG; Kostelecky, VA | Signals for Lorentz violation in post-Newtonian gravity | PHYSICAL REVIEW D | 2006 | 116 |
| B115 | Thiemann, T | Gauge field theory coherent states (GCS): I. General properties | CLASSICAL AND QUANTUM GRAVITY | 2001 | 98 |
| B329 | Tsagas, CG; Challinor, A; Maartens, R | Relativistic cosmology and large-scale structure | PHYSICS REPORTS-REVIEW SECTION OF PHYSICS LETTERS | 2008 | 87 |
| B437 | Centrella, J; Baker, JG; Kelly, BJ; van Meter, JR | Black-hole binaries, gravitational waves, and numerical relativity | REVIEWS OF MODERN PHYSICS | 2010 | 76 |
| B184 | Cane, F; Bear, D; Phillips, DF; Rosen, MS; Smallwood, CL; Stoner, RE; Walsworth, RL; Kostelecky, VA | Bound on Lorentz and CPT violating boost effects for the neutron | PHYSICAL REVIEW LETTERS | 2004 | 74 |
| B500 | Kostelecky, VA; Tasson, JD | Matter-gravity couplings and Lorentz violation | PHYSICAL REVIEW D | 2011 | 57 |
| B331* | Turyshev, SG | Experimental Tests of General Relativity | ANNUAL REVIEW OF NUCLEAR AND PARTICLE SCIENCE | 2008 | 52 |
| B503* | Buchert, T | Toward physical cosmology: focus on inhomogeneous geometry and its non-perturbative effects | CLASSICAL AND QUANTUM GRAVITY | 2011 | 45 |
| B211 | Lane, CD | Probing Lorentz violation with Doppler-shift experiments | PHYSICAL REVIEW D | 2005 | 42 |
| B457 | Wiegand, A; Buchert, T | Multiscale cosmology and structure-emerging dark energy: A plausibility analysis | PHYSICAL REVIEW D | 2010 | 30 |
| B339 | Pun, CSJ; Kovacs, Z; Harko, T | Thin accretion disks onto brane world black holes | PHYSICAL REVIEW D | 2008 | 31 |
| B330* | Rovelli, C | Loop Quantum Gravity | LIVING REVIEWS IN RELATIVITY | 2008 | 29 |
| B338 | Deruelle, N; Sasaki, M; Sendouda, Y | Detuned f(R) gravity and dark energy | PHYSICAL REVIEW D | 2008 | 24 |
| B280 | Turyshev, SG; Israelsson, UE; Shao, M; Yu, N; Kusenko, A; Wright, EL; Everitt, CWF; Kasevich, M; Lipa, JA; Mester, JC; Reasenberg, RD; Walsworth, RL; Ashby, N; Gould, H; Paik, HJ | Space-based research in fundamental physics and quantum technologies | INTERNATIONAL JOURNAL OF MODERN PHYSICS D | 2007 | 23 |
| B565 | Xu, C; Saridakis, EN; Leon, G | Phase-space analysis of teleparallel dark energy | JOURNAL OF COSMOLOGY AND ASTROPARTICLE PHYSICS | 2012 | 30 |
| B379 | Bailey, QG | Time delay and Doppler tests of the Lorentz symmetry of gravity | PHYSICAL REVIEW D | 2009 | 27 |
| B380 | Coc, A; Olive, KA; Uzan, JP; Vangioni, E | Nonuniversal scalar-tensor theories and big bang nucleosynthesis | PHYSICAL REVIEW D | 2009 | 23 |
| B562 | Liu, D; Reboucas, MJ | Energy conditions bounds on f(T) gravity | PHYSICAL REVIEW D | 2012 | 19 |
| B341 | Harko, T; Sabau, VS | Jacobi stability of the vacuum in the static spherically symmetric brane world models | PHYSICAL REVIEW D | 2008 | 14 |
| B566 | Gonzalez, PA; Saridakis, EN; Vasquez, Y | Circularly symmetric solutions in three-dimensional teleparallel, f(T) and Maxwell-f(T) gravity | JOURNAL OF HIGH ENERGY PHYSICS | 2012 | 16 |
| B439 | Centrella, J; Baker, JG; Kelly, BJ; van Meter, JR | The Final Merger of Black-Hole Binaries | ANNUAL REVIEW OF NUCLEAR AND PARTICLE SCIENCE, VOL 60 | 2010 | 13 |
| B585 | Wu, YP; Geng, CQ | Matter density perturbations in modified teleparallel theories | JOURNAL OF HIGH ENERGY PHYSICS | 2012 | 9 |
| B447 | Bohmer, CG; De Risi, G; Harko, T; Lobo, FSN | Classical tests of general relativity in brane world models | CLASSICAL AND QUANTUM GRAVITY | 2010 | 8 |
| B137 | Maartens, R | Brane-world cosmological perturbations - A covariant approach - | PROGRESS OF THEORETICAL PHYSICS SUPPLEMENT | 2002 | 3 |
| B589 | Baccetti, V; Tate, K; Visser, M | Lorentz violating kinematics: threshold theorems | JOURNAL OF HIGH ENERGY PHYSICS | 2012 | 3 |
| B179 | Sasaki, M | Brane-world cosmology and inflation | PRAMANA-JOURNAL OF PHYSICS | 2004 | 1 |
| B400 | Harko, T | Matter Accretion by Brane-World Black Holes | JOURNAL OF THE KOREAN PHYSICAL SOCIETY | 2009 | 0 |
| B558 | Baccetti, V; Tate, K; Visser, M | Inertial frames without the relativity principle | JOURNAL OF HIGH ENERGY PHYSICS | 2012 | 0 |
* asterisk signifies the top 5 core nodes.
References
- D.J. Watts, S.H. Strogatz, Collective dynamics of 'small-world' networks, Nature, 393(6684), 440-442(1998).
- A.- L. Barabási, R. Albert, Emergence of scaling in random networks, Science, 286(5439), 509-512(1999).
- R. Albert, A.-L. Barabási, Statistical mechanics of complex networks, Review of Modern Physics, 74(1): 47–97(2002).
- A. Barrat, M. Barthélemy, R. Pastor-Satorras, and A. Vespignani, The architecture of complex weighted networks, Proceedings of the National Academy of Sciences of the USA, 101(11), 2747-3752(2004).
- K. Börner, S. Sanyal, and A. Vespignani, Network science, Annual Review of Information Science and Technology, 41, 537-607(2007).
- M.E.J. Newman, "Networks: An Introduction", Oxford: Oxford University Press(2010).
- A. Clauset, C. Moore, and M.E.J. Newman, Hierarchical structure and the prediction of missing links in networks, Nature, 453, 98-101(2008).
- M.A. Serrano, M. Boguñáb, and A. Vespignani, Extracting the multiscale backbone of complex weighted networks, Proceedings of the National Academy of Sciences of the USA, 106(16), 6483-6488(2009).
- Y.-Y. Ahn, J. P. Bagrow and S. Lehmann, Link communities reveal multiscale complexity in networks, Nature, 466, 761-765(2010).
- M. E. J. Newman, The structure and function of complex networks, SIAM Review, 45(2): 167-256(2003).
- M. De Domenico, A. Sole´-Ribalta, E. Cozzo, et al., Mathematical Formulation of Multilayer Networks, Physical Review X, 3(4), 041022(2013).
- S. Boccaletti, G. Bianconi, R. Criado, C.I. del Genio, J. Gómez-Gardeñesi, M. Romance, I. Sendiña-Nadal, Z. Wang and M. Zanin, The structure and dynamics of multilayer networks, Physics Reports, 544, 1-122(2014).
- G. Bianconi, Statistical mechanics of multiplex networks: entropy and overlap, Physical Review E, 87, 062806(2013).
- F. Battiston, V. Nicosia, and V. Latora, Structural measures for multiplex networks, Physical Review E, 89, 032804(2014).
- G. Menichetti, D. Remondini, P. Panzarasa, R. J. Mondragon and G. Bianconi. Weighted Multiplex Networks, Plos One, 9(6), e97857(2014).
- E. Yan, Y. Ding, Measuring scholarly impact in heterogeneous networks, Proceedings of the American Society for Information Science and Technology, 47(1), 1-7(2010).
- E. Yan, Y. Ding, C. R. Sugimoto, P-Rank: An indicator measuring prestige in heterogeneous scholarly networks, Journal of the American Society for Information Science and Technology, 62(3), 467–477(2011).
- X. Liu, C. Guo, Y. Yu and Y. Sun, Meta-Path-Based Ranking with Pseudo Relevance Feedback on Heterogeneous Graph for Citation Recommendation, Proceedings of the ACM International Conference on Information and Knowledge Management, 121-130(2014).
- X. Liu, Y. Yu, C. Guo, Y. Sun and L. Gao, Full-Text based Context-Rich Heterogeneous Network Mining Approach for Citation Recommendation, Proceedings of the ACM/IEEE Joint Conference on Digital Libraries, 361-370(2014).
- Y. Sun, J. Han, "Mining heterogeneous information networks: principles and methodologies", Morgan & Claypool Publishers (2012).
- J. E. Hirsch, An index to quantify an individual’s scientific research output, Proceedings of the National Academy of Sciences of the USA, 102(46), 6569-16572(2005).
- A. Schubert, A. Korn, A. Telcs, Hirsch-type indices for characterizing networks, Scientometrics, 78(2), 375-382(2009).
- S.X. Zhao, R. Rousseau, F.Y. Ye, h-Degree as a basic measure in weighted networks, Journal of Informetrics, 5(4), 668-677(2011).
- S.X. Zhao, F.Y. Ye, Exploring the directed h-degree in directed weighted networks, Journal of Informetrics, 6(4), 619-630(2012).
- S.X. Zhao, P.L. Zhang, J. Li, A.M. Tan and F.Y. Ye, Abstracting Core Subnet of Weighted Networks Based on Link Strengths, Journal of the Association for Information Science and Technology, 65(5), 984-994 (2014).
- W. Glänzel, The role of core documents in bibliometric network analysis and their relation with h-type indices, Scientometrics, 93(1), 113-123(2012).
- W. Glänzel, B. Thijs, Using ‘core documents’ for the representation of clusters and topics, Scientometrics, 88(1), 297-309(2011).
- W. Glänzel, B. Thijs, Using ‘core documents’ for detecting and labelling new emerging topics, Scientometrics, 91(2), 399-416(2012).
- E. Otte, R. Rousseau, Social network analysis: a powerful strategy, also for the information sciences, Journal of Information Science, 28(6), 441-453(2002).
- S.Boccaletti, V. Latora, Y. Morenod, M. Chavez and D.-U. Hwang, Complex networks: Structure and dynamics, Physics Reports, 424, 175-308(2006).
- S. B. Seidman, Network structure and minimum degree, Social networks, 5(3), 269-287(1983).



