Stealth-Obfuscation Zero Knowledge Proof Authentication Protocol

Edward Danso Ansong^*, James Ben Hayfron-Acquah

Department of Computer Science, Kwame Nkrumah University of Science & Technology, Kumasi, Ghana

Abstract

In this paper we present a password authentication protocol over untrusted networks. This password authentication protocol stores user password in a non-plaintext equivalent therefore a breached database would not reveal enough information about the user password. This protocol relies on the strength of discrete logarithms with the Schnorr Signature Scheme and also goes further to satisfy all properties of a zero knowledge proof system.

Keywords

Dictionary Attacks, Discrete Exponentiation, Zero Knowledge Proof System, Schnorr Signature Scheme

Received: May 14, 2016
Accepted: June 8, 2016
Published online: July 16, 2016

@ 2016 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY license. http://creativecommons.org/licenses/by/4.0/

1. Introduction

User authentication systems have evolved throughout the years with the focus on securely proving a party’s legitimacy to another. These user authentication systems can be categorized as

• What a person is (biometrics)?

• What a person has (tokens, cell phone)?

• What a person knows (password, pin)?

• Where a person is (location)?

to a combination of these factors which is known as a Multi-factor user authentication scheme. Although all these factors are designed to offer some protection against security attacks, the current trends in computing keeps introducing new threats.

This paper will be dealing with a mechanism for authentication for "What the person knows" (Knowledge Factor) category of user authentication. In this scheme, the user’s password and pin are the only secret available to the client whereas the network between the client and server is perceived to be untrusted. The only trusted parties in this authentication are client and the server application requesting the authentication hence the need to verify the knowledge of the secret keys without disclosing enough information about them on the network. Such a scheme requires no more than just the client and the server requesting the authentication hence it is easy to implement in almost all Knowledge factor user authentication scheme since no additional hardware devices are required. To increase the entire security of such a scheme, other factors such as "What the person has" and "What the person is" can be employed as well to make it multi factor.

Knowledge factor authentication schemes have been the primary type of authentication to almost all web and software services. They are basically easy to design and implement in any architecture due to simplicity and low overhead in its implementation as compared to other factors like biometrics and location. Although a factor like the biometrics has proven to be more secure than the traditional Knowledge Factor authentication scheme, most of it implementation is still susceptible to over a decade old trick where finger print are raised from readers and used for authentication. Location based authentication is also a good contender for secure authentication but device latency, availability of device and its services hinders it implementation. Many researches have been carried out in the area of location based authentication and they lay out techniques for authentication, STAT I (Space – Time Authentication Technique) use a GPS for determining a user’s location for authentication whiles the STAT II uses a proprietary IQRF technology for determining its user’s location for authentication [12]. As an alternative to just location-based authentication, Hang et al. proposed a two-factor authentication scheme (location-based authentication with security questions) as a fallback mechanism to other authentication mechanism like a knowledge-based scheme [13]. After implementation and testing of their proposed scheme, they found out that around 90% of their users were able to remember the locations to security questions within a 30 meter range whiles attackers could not successfully guess such locations [13].

2. Related Works

Building authentication schemes with zero-knowledge proofs has been researched and implemented in many flavors along the years. The need to provide such secure authentication schemes for web applications and services has been driven by the influx of mobile devices and internet in our daily lives. Some of the researches in Zero Knowledge Proof Authentication Schemes are as follows: "NARWHALL-An implementation of zero knowledge authentication" [2]. In this paper they discussed several vulnerabilities in existing website authentication systems and NARWHALL as a more secure alternative to such authentication systems. NARWHALL fixes most of the discussed vulnerabilities by building on an original protocol described by Lum Jia Jun [11]. The protocol described by Lum Jia Jun is based on the Zero Knowledge Authentication with Zero Knowledge framework which allows an easy implementation of Zero Knowledge Authentication [11]. In [11] the available values to the prover of the system is his password and a public key, and the available values to the verifier of the system is the same public key as the prover’s and a pseudonym of the user which would will be calculated for during any authentication round. NARWHALL builds on such protocol by adding more components for more secure authentication. During a signup session with NARWHALL, a username, password of the user is entered and also the websites public unique identifier, the password is hashed and a public key is generated from it. The website unique identifier prevents users with the same username and password from two website to have the same public key and also the username prevents users of the same website to have the same public key. During a login session to a random challenge is sent to the users login form and stored in a cookie; on any login attempt the cookie information is updated to prevent brute forcing. Some implementation issues were identified the worse of all being the dependence of Javascript for client side processing. In browsers with disabled Javascript, the whole authentication fails. Another issue could be attributed to salting the user’s password before generating a pseudonym for the user. The user’s password were not salted hence an attacker could pre-compute values of the credentials and submit it for authentication.

Sławomir et al. proposed a Zero Knowledge Proof Authentication based on isomorphic graphs which allows authentication with varying confidence and also security level [14]. This protocol follows strictly the ZKP challenge – response round for an authentication, so AJAX and xml are used to meet the requirement. During authentication a user makes a request and a server responds with a challenge and a user replies with a response and the server sends its final response denoting a successful or failed login attempt this is simulated with AJAX and XML. In an authentication process, a user enters his username and password and the browser calculate a public and private key pair. The browser then calculate a challenge graph and sends it to the server and the server replies with a random challenge to the browser and the browser then chooses a response to the challenge and sends it to the browser. A response is finally sent from the server to the browser which denotes a successful authentication or failure. The public keys in this protocol are represented with two isomorphic graphs  and the permutation of  is the private key. During authentication a prover will generate a random permutation and sends a graph  to the verifier (server) and depending on the challenge sent to the prover, the prover responds with either  then the verifier is able to check if the private and public keys are valid. In this implementation there could be attacks on the Graph isomorphism if an algorithm with Corneil et al. [16] algorithm which determines if two graphs are isomorphic thereby increasing the speed of brute force attacks on it. Furthermore this implementation is also susceptible to dictionary attacks, hence when a website is breached and user login details are stolen, it could be used to attack this implementation.

Thiruvaazhi et al. proposed an elliptic curve discrete logarithm zero knowledge proof protocol for proving a user’s binding to a public key and also his possession of a private key [15]. In their scheme a user’s visited domain is hashed and encoded and sent to the web server and the web server responds with its actual public key and it is hashed and encoded by the user and also verified against the original encoded hash of the domain name during registration to check it validity. In proving the private key, an elliptic curve will be generated over a finite field; a prover will choose a random value and compute the witness and send it to a verifier. A verifier will also randomly choose a challenge as either 0 or 1 and sends it to the prover and the prover will respond based on the challenge and finally the verifier will compute the validity of the response based on the prover’s response. In this implementation there were some performance issues because of the iterations needed for the Zero Knowledge Proof challenge – response authentication round which could be detriment to its implementation on mobile platforms.

3. Zero Knowledge Proofs

A zero-knowledge proof is a method by which one party can prove to another that a statement is true by disclosing no other information than the fact that the statement is true. A derivative of this scheme is the Zero Knowledge Proof of Knowledge which allows a prover to prove to a verifier that a statement is true and also possesses a witness for the fact [10]. For an authentication system to be zero knowledge it has to be

• Complete

• Sound

• Zero-Knowledge

A system is complete when a prover can convince the verifier that a statement is true and no cheating prover can convince the verifier otherwise and it is sound if when a statement is false no cheating prover can convince the verifier that it is true and it is zero-knowledge when a cheating verifier can only learn that the statement is true. Zero knowledge proofs are interactive protocols with zero knowledge. Interactive proof system was introduced by Babai - [4] and the Zero Knowledge by Goldwasser et al. [5]. Although the study of Zero Knowledge Proofs is primarily focused on user authentication, it can further be implemented in digital payment systems [1], and electronic voting systems [6].

4. Schnorrs Identification Protocol

This is a three move protocol in which the exchanged messages; the commitment, challenge and response are exchanged between a prover and verifier to be able to prove the knowledge of a secret key. The first step involves the prover sending a commitment to the verifier and the verifier responding with a challenge and finally the prover sending its response for final verification of the knowledge secret key. To describe this scheme we can define the values available to the prover as (g, q, y, and x) and that of the verifier as (g, q, and y) where g, q and y are public keys and x is the secret key only known by the prover

• Commitment

Prover:  =>  

• Challenge

• Response

Prover:

Verifier:

Let  be a generator of G (a finite group of order q). Let  be the public key of the prover and x the secret key, we can then prove the knowledge of the secret key.

Such proofs of knowledge are useful in the construction of signature schemes.

5. Schnoors Signature Scheme

This is a digital signature scheme which is a variant of the ElGamal Signature scheme [1]. It is efficient and generates shorter signatures as compared to the ElGamal signature scheme. A Schnorr signature of message  is a pair (c, s) with  and satisfying the verification equation  where H is a collision-resistant cryptographic hash function  that maps to a fixed hashed output.

• Key Generation Phase: Secret Key = x,

• Message Signing Phase:

1.  Choose a Random r from a set

2. 

3. 

4.   (mod q)

• Verification Phase:

 =

For correctness of the scheme we can verify it by using the values .

The verification phase shows how a signed message can be verified by the other party.

6. Signatures Based on Proofs of Knowledge – (SPK)

Signature based on proofs of knowledge is used to prove the possession of secret keys [7]. For a pair  satisfying  with s = and V =  is an SPK of the discrete logarithm of a group element y to the base of g of the message  and is denoted . For an , the secret value can be expressed in terms of the public key as  where x is the secret value and the random integer from the set  can be expressed as . The challenge can be expressed as  and the response as . A general notation of a proof of knowledge of the secret keys  can be expressed as .

7. Our Scheme

Our scheme relies on  for website authentication. The strength of our scheme as compared to NARWHAL (a challenge-response model authentication based on zero knowledge proofs) [2] is based on the complexity of how passwords are stored. It doesn’t share weakness with hashed passwords since an attacker with pre-computed values of passwords would not be able to look it up. Our scheme offers a stealth authentication over networks since not much information is leaked on the network during an authentication round.

8. Our Implementation

a)  User Registration

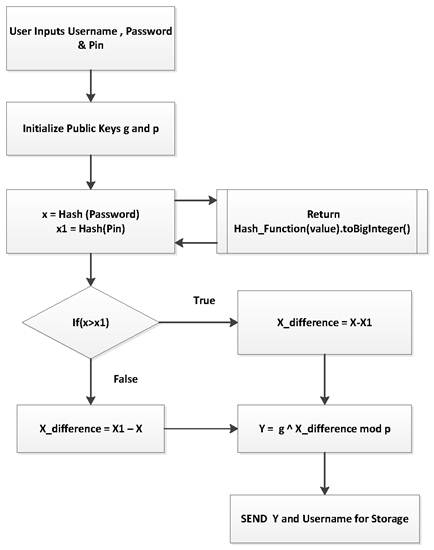
Figure 1. Stealth ZKP User Registration (Client Side).

In the user registration process, a user chooses a username, password and pin of their choice and their pin and password are hashed with a collision -resistant hash function and converted to big integers [1]. A difference of the larger value from the smaller value is taken and computed with the cryptographic group element  as  and stored with the username to the server. The value stored on the server does not reveal enough information about the private key of the client being (. The value stored on the server  becomes the user’s public key.

b)  User Sign In (Client Side)

During sign-in the user enters his username, password and pin as they registered with and the password and pin are hashed using the same collision-resistant hash function as at signup and the values converted to big integer values for further computation. From  we can set our message parameter to null () [1] and deduce the signing as follows:

1) 

2) 

3) 

4) 

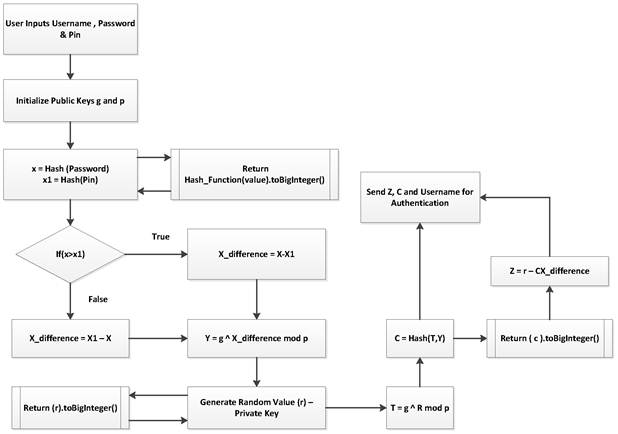
Figure 2. Stealth ZKP User Authentication (Client Side).

The client sends (C and z) to server for authentication.

c)  User Sign In – (Server Side)

At the user authentication at server side, the process has to be proved for correctness.

1) 

2) 

3) 

4) 

For any round of authentication valid credentials can be verified.

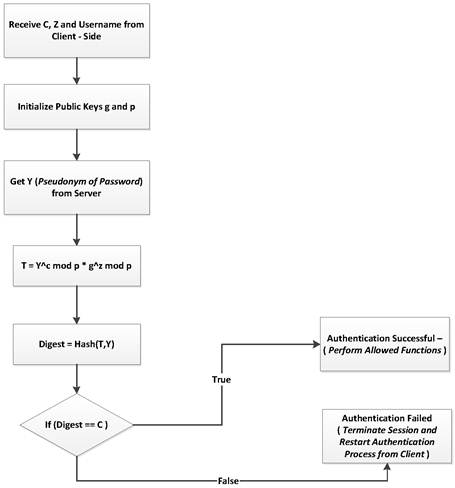
Figure 3. Stealth User Authentication (Server Side).

9. Strength of Our Scheme

The strength of our protocol is based on the strength of the discrete logarithm problem. The protocol will be able to solve the problem of user authentication over unsecure networks. During authentication, a user submits his public key and private key for authentication hence no other knowledge of the password is known. On unsecure networks, data sniffed would not reveal anything much about the user’s secret key hence it cannot be replayed for another authentication session. The intractability of discrete logarithms and its easy implementation makes it a better candidate over Visual Cryptography, Pairing based Cryptography and Elliptic Curves for Zero Knowledge Proofs [8] [9].

10. Conclusion and Further Works

With the defined problems addressed in this paper, we can implement our zero knowledge proof implementation code-named Stealth Knowledge Authentication for devices with minimal computational resource. With HTTPS providing a secure transmission of authentication details and our Javascript assets files, we implement it to protect user details before and after transmission.

Although our implementation requires JavaScript which is supported by most browsers, some users disable it which would prevent it to run on such systems and also the authentication scheme is not multi – factor, which would make it susceptible to attack when the user’s secret keys are known. Our implementation also doesn’t follow the classical Zero Knowledge Proof Authentication’s Challenge – Response round hence there could be a slight chance of a cheating verifier proving him or herself as an honest verifier hence Ajax and Sockets could be used to implement it hence reducing it iterating challenges.

References

1. Jan Leohard Camenisch, "Group Signature Schemes and Payment Systems Based on the Discrete Logarithm Problem", 1998.
2. Ryan Cheu, Patrick Yang, Alexander Lin and Alexander Jaffe, "NARWHALL-An implementation of zero knowledge authentication", 2014.
3. Wu, Thomas D, "The Secure Remote Password Protocol." 1998.
4. Babai, L., Trading group theory for randomness. Seventeenth Annual ACM Symposium on Theory of Computing, (pp. 421–429). Rhode Island, 1985.
5. Shafi Goldwasser, S.M, The knowledge complexity of interactive proof systems. 27th Annual Symposium on Foundations of Computer, (pp. 291–304). 1985.
6. Lynn, B. E- Voting – Stanford Cryptography, 2003.
7. Schnorr, C. P. Efficient signature generation for smart. Journal of Cryptology, 239–252. 1991.
8. Scott, M. M-Pin: A Multi-Factor Zero Knowledge. Certivox Labs, 2013.
9. Zhang, D. M. Zero-knowledge proofs of identity based on ELGAMAL on conic. E-Commerce Technology for Dynamic E-Business. IEEE International Conference. 2004.
10. Amos Fiat, U. F. Zero-knowledge proofs of identity. Journal of Cryptology, 77–94. 1988.
11. Lum Jia Jun, Brandon. Implementing zero-knowledge authentication with zero knowledge. The Python Papers Monograph 2.9 (2010).
12. David Jarosm Radek Kuchta. New Location – Based Authentication Techniques in the Access Management. Wireless and Mobile Communications 6^th International Conference, 2010.
13. Hang A, De Luca A, Smith M, Richter M, Hussmann H. Where Have You Been? Using Location-Based Security Questions for Fallback Authentication. Eleventh Symposium On Usable Privacy and Security (SOUPS2015), 2015.
14. Slawomir Grzonkowski, Wojciech Zaremba, Maciej Zaremba, Bill McDaniel. Extending Web Applications with a Lightweight Zero Knowledge Proof Authetication, 2008.
15. U. Thiruvaazhi, R. Divya. Web Application Protocol Using Zero Knowledge Proofs, Information Security Journal, 20:112-121, 2011.
16. D. G. Corneil, C. C. Gotlieb. An efficient algorithm for graph isomophism. J. ACM, 51-64, 1970.