A Study on Discrete Model of a Typical Three Species Syn-Ecology with Limited Resources
B. Hari Prasad*
Department of Mathematics, Chaitanya Degree College (Autonomous), Hanamkonda, Telangana State, India
Abstract
In this paper, we study on a three species discrete model syn ecology with limited resources. The system comprises of a commensal (S1), two hosts S2 and S3ie., S2 and S3 both benefit S1, without getting themselves effected either positively or adversely. Further S2 is a commensal of S3 and S3 is a host of both S1, S2. The basic equations for this model constitute as three first order non-linear coupled ordinary difference equations. All possible equilibrium points are identified based on the model equations and criteria for their stability are discussed. The model would be stable if absolute value of each of the eigen values of the characteristic equation is less than one.
Keywords
Commensal, Eigen Value, Equilibrium Point, Host, Stable, Unstable
Received: April 9, 2015
Accepted: May 1, 2015
Published online: May 22, 2015
@ 2015 The Authors. Published by American Institute of Science. This Open Access article is under the CC BY-NC license. http://creativecommons.org/licenses/by-nc/4.0/
1. Introduction
Ecology, a branch evolutionary biology, deals with living species that coexist in a physical environment that sustain themselves on common resources. It is a common observation that the species of same nature can not flourish in isolation without any interaction with species of different kinds. Syn-ecology is an ecosystem comprised of two or more distinct species. Species interact with each other in one way or other. The Ecological interactions can be broadly classified as Ammensalism, Competition, Commensalism, Neutralism, Mutualism, Predation, Parasitism and so on. Lotka[1], Svirezhev et al [2] and Volterra [3] pioneered theoretical ecology significantly and opened new eras in the field of life and biological sciences. The authors Rogers et al [4], Varma [5] and Veilleux [6] discussed prey-predator, competing ecological models. Colinvaux [7] and Smith [8] studied basic concepts of population models in ecology.
Mathematical Modeling plays a vital role in providing insight into the mutual relationships (positive, negative) between the interacting species. The general concepts of modeling have been discussed by several authors Kapur [9], Kushing [10], Meyer [11] and Pielou [12]. Srinivas [13] studied the competitive ecosystem of two species and three species with limited and unlimited resources. Later, Narayan et al [14]studied prey-predator ecological models with partial cover for the prey and alternate food for the predator. Acharyulu et al [15,16] derived some productive results on various mathematical models of ecological Ammensalism with multifarious resources in the manifold directions. Further, Kumar [17] studied some mathematical models of ecological commensalism. The present author Prasad [18-21] investigated continuous and discrete models on the three species syn-ecosystems.
The present investigation is on an analytical study of a typical three species (S1, S2, S3) syn-eco system. The system comprises of a commensal (S1), two hosts S2 and S3ie, S2 and S3 both benefit S1, without getting themselves effected either positively or adversely. Further S2 is a commensal of S3 and S3 is a host of both S1, S2. Commensalism is a symbiotic interaction between two populations where one population (S1) gets benefit from (S2) while the other (S2) is neither harmed nor benefited due to the interaction with (S1). The benefited species (S1) is called the commensal and the other, the helping one (S2) is called the host species. A common example is an animal using a tree for shelter-tree (host) does not get any benefit from the animal (commensal).Some more real-life examples of commensalism are, i. The clownfish shelters among the tentacles of the sea anemone, while the sea anemone is not effected. ii. A flatworm attached to the horse crab and eating the crab’s food, while the crab is not put to any disadvantage. iii. Sucker fish (echeneis) gets attached to the under surface of sharks by its sucker. This provides easy transport for new feeding grounds and also food pieces falling from the sharks prey, to Echeneis.
2. Material and Methods
2.1. Notation Adopted
S1: Commensal of S2 andS3;S2: Host of S1 and commensal of S3;S3: Host of S1 and S2; Ni(t): The population strength of Si at time t, i = 1,2,3;t: Time instant; ai: Natural growth rate of Si , i = 1,2, 3;aii:Self inhibition coefficients of Si, i=1, 2, 3;a12,a13: Interaction coefficients of S1 due to S2 and S1 due to S3;a23: Interaction coefficient of S2 due to S3.Further the variables N1, N2, N3 are non-negative and the model parameters a1, a2, a3, a11, a22, a33, a13, a23 are assumed to be non-negative constants.
2.2. Theoretical Framework: Basic Equations
Consider the non-linear autonomous system of discrete difference equations
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
The equations (1),(2) and (3) can be written in terms of recurrence relations as
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
where![]()
The equilibrium states for the given system are obtained by solving the equations at
![]()
We get,
![]()
![]()
![]()
![]()
![]()
where
![]()
![]()
where
![]()
![]()
where
![]()
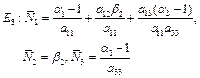
2.3. Stability of the Equilibrium States
The basic equations can be linearized about the equilibrium point ![]() .
.
We get,
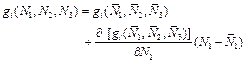
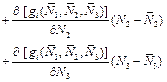
where![]()
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
The above equations can be written in the matrix notation as,
![]() .
.
where
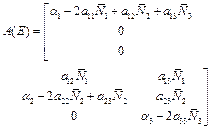 (10)
(10)
and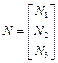
The characteristic equation for the system is
det[A – lI] = 0 (11)
The equilibrium point ![]() is stable, if absolute value of each of the eigen values of the characteristic equation (11) is less than one.
is stable, if absolute value of each of the eigen values of the characteristic equation (11) is less than one.
2.3.1. Stability of E1
In this case, we get,
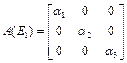
The eigen values of the matrix A(E1)are α1, α2, α3.Since, the absolute values of these three are greater than or is equal to one. i.e,![]() .
.
Hence, E1 (0, 0) is unstable.
2.3.2. Stability of E2
In this case, we get,

The eigen values of the matrix A(E2)are ![]() .
.
Since, the absolute value of all these eigen values is less than one only when
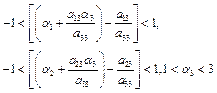
Hence, E2 is stable.
2.3.3. Stability of E3
In this state, we have,
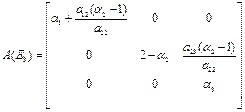
The eigen values of the matrix A(E3)are![]() .
.
Since, ![]() .Hence, E3 is unstable.
.Hence, E3 is unstable.
2.3.4. Stability of E4
In this state, we have,
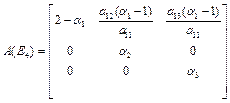
The eigen values of the matrix A(E4) are![]() .
.
Since,![]() .Hence, E4 is unstable.
.Hence, E4 is unstable.
2.3.5. Stability of E5
In this case,
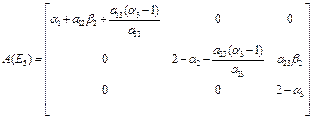
The eigen values of the matrix A(E5)are 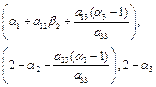 . Since, the absolute value of all these eigen values is less than one only when
. Since, the absolute value of all these eigen values is less than one only when
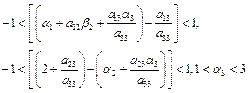
Hence, E5 is stable.
2.3.6. Stability of E6
In this case,
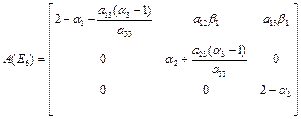
The eigen values of the matrix A(E6)are ![]()
Since, the absolute value of all these eigen values is less than one only when

Hence, E6 is stable.
2.3.7. Stability of E7
In this state,
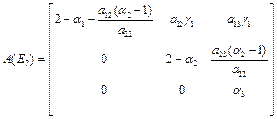
The eigen values of the matrix A(E7)are ![]()
Since, ![]() . Hence, E7 is unstable.
. Hence, E7 is unstable.
2.3.8. Stability of E8
In this state,
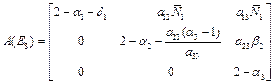
The eigen values of the matrix A(E8)are ![]()
where![]()
Since, the absolute value of all these eigen values is less than one only when
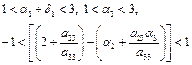
Hence, E8 is stable.
3. Discussion
Investigate some relation-chains between the species such as Prey-Predation, Neutralism, Commensalism, Mutualism, Competition and Ammensalism between three species (S1, S2, S3) with the population relations.
The present paper deals with an investigation on a typical three species discrete model syn eco-system. The system comprises of a commensal (S1), two hosts S2 and S3ie., S2 and S3 both benefit S1, without getting themselves effected either positively or adversely. Further S2 is a commensal of S3 and S3 is a host of both S1, S2. It is observed that, in all eight equilibrium states, only the four states E2,E5,E6,E8 are stable and rest of them unstable.
Acknowledgment
I thank to Professor (Retd), N.Ch.PattabhiRamacharyulu, Department of Mathematics, National Institute of Technology, Warangal (T.S.), India for his valuable suggestions and encouragement.
References
- Lotka, A.J.(1925), Elements of Physical Biology, Williams and Wilking, Baltimore.
- Svirezhev, Yu.M.,Logofet, D.O.(1983), Stability of Biological Community, MIR, Moscow.
- Volterra, V.(1931), Leconssen La TheorieMathematique De La LeittePouLavie, Gauthier-Villars, Paris.
- Rogers, D.J., Hassell, M. P.(1974), General models for insect parasite and predator searching behavior: Interference, Journal Anim. Ecol., 43, 239 - 253.
- Varma, V.S.(1977), A note on Exact solutions for a special Prey - Predator or competing species system, Bull. Math. Biol., 39, 619 - 622.
- Veilleux, B.G.(1979), An analysis of the predatory interaction between paramecium &Didinium, Journal Anim. Ecol., 48, 787 - 803.
- Colinvaux, A.P.(1986), Ecology, John Wiley, New York.
- Smith, J. M.(1974), Models in Ecology, Cambridge University Press, Cambridge.
- Kapur,J.N.(1985), Mathematical Modeling in Biology & Medicine, Affiliated East West.
- Kushing, J.M.(1977), Integro-Differential Equations and Delay Models in Population Dynamics, Lecture Notes in Bio-Mathematics, Springer Verlag, 20.
- Meyer, W.J.(1985), Concepts ofMathematical Modeling, Mc.Grawhill.
- Pielou, E.C.(1977), Mathematical Ecology, John Wiley and Sons, New York.
- Srinivas, N.C.(1991), Some Mathematical Aspects of Modeling in Bio-medical Sciences, Kakatiya University, Ph.D Thesis.
- Narayan, K.L., Pattabhiramacharyulu, N.Ch.(2007), A Prey-Predator Model with Cover for Prey and Alternate Food for the Predator and Time Delay, Int. Journal of Scientific Computing, 1, 7 - 14.
- Acharyulu, K.V.L.N., Pattabhiramacharyulu, N.Ch.(2010), An Enemy- Ammensal Species Pair With Limited Resources –A Numerical Study, Int. Journal Open Problems Compt. Math., 3,339-356.
- Acharyulu, K.V.L.N., Pattabhiramacharyulu, N.Ch.(2011), An Ammensal-Prey with three species Ecosystem,International Journal of Computational Cognition , 9, 30 - 39.
- Kumar, N.P.(2010), Som Mathematical Models of Ecological Commensalism,AcharyaNagarjuna University, Ph.D. Thesis.
- Prasad, B.H.(2014), On the Stability ofaThree Species Syn- Eco-System with Mortality RatefortheSecond Species. Int. Journal of Social Science & Interdisciplinary Research, 3, 35-45.
- Prasad, B.H.(2014), The Stability Analysis of a Three Species Syn-Eco-System with MortalityRates. Contemporary Mathematics and Statistics, 2, 76-89.
- Prasad, B.H.(2014), A Study on DiscreteModelofThreeSpeciesSyn-Eco-System with Limited Resources. Int. JournalModern Education and Computer Science,11, 38-44.
- Prasad, B.H.(2014), A Discrete Model of a Typical Three Species Syn- Eco – System with Unlimited Resources for the First and Third Species. Asian Academic Research Journal of Multidisciplinary,1, 36-46.



